How to use LaTeX in comments

WordPress has the ability to insert LaTeX math displays (e.g. $\int_{-\infty}^\infty e^{-\pi x^2}\ dx = 1$ ) into both posts and comments. The format for this is “$latex [Your LaTeX code]$” (but without the brackets, of course). See this announcement for details.

There used to be a number of quirks with the WordPress LaTeX plugin, but they have now largely been fixed. If you find any problems, please report them at this page.

WordPress also supports a certain amount of HTML. As a consequence, be careful with using the < and > signs in a comment, they may be misinterpreted as HTML tags! You can use < and > instead. (Inside of a LaTeX environment, you can use \lt and \gt.)

In case a comment really gets mangled up by formatting errors, contact one of the moderators of the polymath project, so that he or she can manually correct it.

The comments to this post will serve as the LaTeX help forum and LaTeX sandbox for this blog. If you want to test out some LaTeX code in the comments below, you may wish to first describe the code without the “latex” symbol in order to show other readers what you are doing. For instance: “Here is a LaTeX test: $a^n+b^n=c^n$ becomes $a^n+b^n=c^n$ “. (Note that one can also mouse over a compiled LaTeX image to recover the original LaTeX source.)

Comments (58)

58 Comments »

the line $\mathbf{R} v$

Comment by Anonymous — October 17, 2011 @ 2:15 pm | Reply
this is a test
$x^2 + x – 1 = 0$

Comment by M Wall — June 20, 2013 @ 8:44 am | Reply
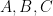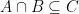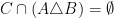This might be an obvious question, but to have a sunflower with three petals, is to find three sets $A,B,C$ , so that $A \cap B \subseteq C$ , and $C \cap (A \triangle B)=\emptyset$ .

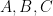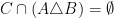What happens if instead of both properties, just one of them is forbidden? For example, if we forbid three sets $A,B,C$ in our family, so that $C \cap (A \triangle B)=\emptyset$ ?

Comment by ILan — November 8, 2015 @ 2:59 pm | Reply
The \gt and \lt don’t seem to be working: I’m trying to compile $a \gt b$: $a \gt b". But$ a>b$ works, see $a>b$

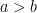
Comment by Anonymous — March 7, 2016 @ 3:01 pm | Reply
I will try to use Latex to express the process but there is no telling how it will turn out

$Z_t \: is \:IID \: N(0,1)\\\\ X_t=Z_t \: if\: t \:is\: even\\\\ X_t=\frac{Z_{t-1}^2 -1}{\sqrt{2}} \: if\: t \:is\: odd$

Comment by PJKar — May 24, 2016 @ 8:21 pm | Reply
$\displaystyle \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}$

Comment by Anonymous — December 11, 2016 @ 6:21 pm | Reply
$a_2^3$

Comment by junkmailer — February 10, 2017 @ 7:21 pm | Reply
This is a test:
$latex[x^2 + \phi]$

Comment by Anonymous — March 7, 2017 @ 4:35 am | Reply
I think I understand now. For the operator norm question, $R$ has eigenvalues $\frac{1}{\lambda_i - (a+bi)$ which are bounded above by $1/|b|$ .

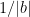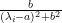For the positive definite imaginary part, I am still a bit confused. The imaginary part of $R$ does not even seem to be Hermitian. But I think I see how to get the conclusion that follows anyway: The eigenvalues above have positive imaginary part $\frac{b}{(\lambda_i - a)^2 + b^2}$ . Using the fact that $R$ has an orthogonal eigenbasis, you can now calculate that the $X^* R X$ has a nonnegative imaginary part for any $X$ .

Is this what it means for the imaginary part of $\latex R$ to be positive definite?

Comment by hhh — March 19, 2017 @ 6:11 pm | Reply
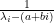I think I understand now. For the operator norm question, $R$ has eigenvalues $\frac{1}{\lambda_i - (a+bi)}$ which are bounded above by $1/|b|$ .

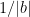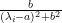For the positive definite imaginary part, I am still a bit confused. The imaginary part of $R$ does not even seem to be Hermitian. But I think I see how to get the conclusion that follows anyway: The eigenvalues above have positive imaginary part $\frac{b}{(\lambda_i - a)^2 + b^2}$ . Using the fact that $R$ has an orthogonal eigenbasis, you can now calculate that the $X^* R X$ has a nonnegative imaginary part for any $X$ .

Is this what it means for the imaginary part of $\latex R$ to be positive definite?

Comment by hhh — March 19, 2017 @ 6:12 pm | Reply
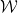This proposition is true, though you’re quite right that I should have mentioned it. Here’s a proof sketch: If $\mathcal{E}$ is immodest, then it generates what I called in the proof of Proposition 2 an ‘immodest S5’ Kripke frame—i.e., the relation $R$ partitions $\mathcal{W}$ into equivalence classes, where each equivalence class $[w]_R = \langle \mathcal{E} = \mathcal{E}_w \rangle$ . 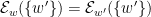Then, for each pair of worlds $w, w' \in \mathcal{W}$ , either $\mathcal{E}_w(\{ w' \}) = \mathcal{E}_{w'}(\{ w' \})$ (if $w' \in [w]_R$ ) or $\mathcal{E}_w(\{ w' \}) = 0$ (if $w' \notin [w]_R$ ). 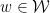So, for each $w \in \mathcal{W}$ ,

$\langle \mathcal{E}(\{w\}) = \mathcal{E}_w(\{w\}) \rangle = \langle \mathcal{E} = \mathcal{E}_w \rangle$

And thus, if you treat $\mathcal{E}$ as a local expert,

Comment by jdmitrig — June 19, 2017 @ 10:04 pm | Reply
this is a latex test
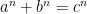Theorem 1
$a^n+b^n=c^n$ .

Proof
too short to write

in a comment.

Comment by Anonymous — September 3, 2017 @ 9:21 pm | Reply
Test

$\mathcal{F}$

Comment by Anonymous — September 4, 2017 @ 4:28 pm | Reply
$7\frac{3}{4}+2\frac{1}{2}$

Comment by Anonymous — September 12, 2017 @ 7:03 am | Reply
$\mathbb{E} \geq \ldots \geq 1$

Comment by min — November 13, 2017 @ 3:09 pm | Reply
$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^s}$

Comment by Any — February 7, 2018 @ 1:18 pm | Reply
\displaystyle \sum_{n=1}^\infty \frac{1}{n^2} = \frac{\pi^2}{6}
hotmail account

Comment by hotmail123 — June 5, 2018 @ 9:47 am | Reply
$latexP(X\leqx)$

Comment by Anonymous — September 16, 2018 @ 7:43 pm | Reply
$P(X \leq x)$

Comment by Anonymous — September 16, 2018 @ 7:47 pm | Reply
This is a latex test:
$e^x = 1 + x + /frac {x^2} {2!} + . . . $

Comment by Anonymous — April 23, 2019 @ 1:59 am | Reply
$a^2 = b^2 + c^2$

Comment by Anonymous — April 23, 2019 @ 2:00 am | Reply
$latexa^2=b^2+c^2$

Comment by Anonymous — April 23, 2019 @ 2:01 am | Reply
$i\hbar$

Comment by Anonymous — April 23, 2019 @ 2:04 am | Reply
$i\hbar s^3$

Comment by Anonymous — April 23, 2019 @ 2:05 am | Reply
$hello$

Comment by Anonymous — May 12, 2019 @ 3:02 pm | Reply
\displaystyle \ 28,19-20-0,28 = 7,91 &s=3

Comment by Igor Moreira — June 2, 2019 @ 5:58 pm | Reply
$i\hbar\frac{\partial}{\partial t}\left|\Psi(t)\right>=H\left|\Psi(t)\right>$

Comment by Angela Chan — September 26, 2019 @ 7:18 am | Reply
Thank you

Comment by dahaiyi — January 12, 2020 @ 1:54 pm | Reply
$trying^2$

Comment by martinskirossinski — March 24, 2020 @ 1:11 am | Reply
[…] For those who want to experiment with what LaTeX does and doesn’t work in comments, you can experiment here. […]

Pingback by MitPY 2: Change of Base in Logarithms – BAD MATHEMATICS — March 24, 2020 @ 11:21 pm | Reply
latex$ “\frac{\mathrm{d} y }{\mathrm{d} x} = \lim_{\delta \rightarrow 0} \delta y /\delta x”$

Comment by sr — April 27, 2020 @ 6:46 am | Reply
$\left( \begin{matrix} {{a}_{11}} & {{a}_{12}} & {{a}_{13}} \\ {{a}_{21}} & {{a}_{22}} & {{a}_{23}} \\ {{a}_{31}} & {{a}_{32}} & {{a}_{33}} \\ \end{matrix} \right)$

Comment by Anonymous — May 24, 2020 @ 5:36 am | Reply
$\displaystyle \mathrm x^2+3x-4=0$

Comment by Eri Costa — February 14, 2021 @ 11:07 am | Reply
$\latex \psi(.)$

Comment by ldragodestructor — March 19, 2021 @ 6:04 am | Reply
$ \psi(.)$

Comment by ldragodestructor — March 19, 2021 @ 6:04 am | Reply
$\psi(.)$

Comment by ldragodestructor — March 19, 2021 @ 6:05 am | Reply
This is a test

$a^2 b^2$

Comment by Malena — June 24, 2021 @ 5:13 pm | Reply
$i\hbar\frac{\partial}{\partial t}\left|\Psi(t)\right>=H\left|\Psi(t)\right>$

Comment by Anonymous — February 20, 2022 @ 1:28 pm | Reply
$= \frac{{(1.10 + 0.9)}}{{150}} = \frac{1}{{75}}$

Comment by Anonymous — February 20, 2022 @ 3:52 pm | Reply
$\frac{{(1.10 + 0.9)}}{{150}} = \frac{1}{{75}}$

Comment by Anonymous — February 20, 2022 @ 3:53 pm | Reply
$= \frac{{(1.10 + 0.9)}}{{150}} = \frac{1}{{75}}$

Comment by Anonymous — February 20, 2022 @ 3:54 pm | Reply
testin….. $x^2 + \frac{1}{2}$

Comment by Anonymous — November 30, 2022 @ 1:07 pm | Reply
$x^2$

Comment by Anonymous — February 26, 2023 @ 4:25 am | Reply
test $x^2$

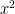
Comment by Anonymous — June 4, 2023 @ 3:27 pm | Reply
testic $x^2 3$

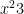
Comment by Anonymous — June 4, 2023 @ 3:28 pm | Reply
testifc $x^2 3$

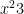
Comment by Matk — June 4, 2023 @ 3:29 pm | Reply
\frac{{100^2z}}{{(100 + x)(100 + y)}}

Comment by Anonymous — September 17, 2023 @ 8:46 am | Reply
\frac{{100^2z}}{{(100 + 20)(100 – 25)}} = \frac{{10000z}}{{120 \cdot 75}} = \frac{{10z}}{9}

Comment by Anonymous — September 17, 2023 @ 8:47 am | Reply
- $latex\[\frac{a}{b}\]$
  
  Comment by Anonymous — September 17, 2023 @ 9:47 am | Reply
$latex\[\frac{a}{b}\]$

Comment by Anonymous — September 17, 2023 @ 9:44 am | Reply
$\frac{{100^2z}}{{(100 + 20)(100 - 25)}} = \frac{{10000z}}{{120 \cdot 75}} = \frac{{10z}}{9}$

Comment by Anonymous — September 17, 2023 @ 6:32 pm | Reply
$lceil epsilon n rceil {n choose k}$

Comment by Calum Shearer — March 20, 2024 @ 2:33 pm | Reply
$epsilon n$

Comment by Calum Shearer — March 20, 2024 @ 3:00 pm | Reply
$epsilon$

Comment by Calum Shearer — March 20, 2024 @ 3:07 pm | Reply
$epsilon$

Comment by Calum Shearer — March 20, 2024 @ 3:09 pm | Reply
$delta^2$

Comment by Calum Shearer — March 20, 2024 @ 3:10 pm | Reply
WordPress comments appear to delete backslashes:

“$ \epsilon$” (with ‘latex’ after dollar sign) gives me:

$\epsilon$

Comment by Calum Shearer — March 20, 2024 @ 3:26 pm | Reply
First line above should be “$ \epsilon$”

Comment by Calum Shearer — March 20, 2024 @ 3:27 pm | Reply

RSS feed for comments on this post. TrackBack URI

	Anonymous on Rota’s Basis Conjecture:…
	Cherrypick India on Polymath projects 2021
	tanner808 on Polymath projects 2021
	Anonymous on Polymath 11 is Now Open
	Chenxiao Tian on Polymath 11 is Now Open
	ryeguy10 on Polymath 11 is Now Open
	ndnnnd on Polymath projects 2021
	Prime time on Two polymath (of a sort) propo…
	What comes after exp… on Minipolymath2 project: IMO 201…
	Will AI Replace Math… on Spontaneous Polymath 14…
	gui7575 on A new polymath proposal (relat…
	Thomas Vu on Polymath projects 2021
	Mary Megrant on Polymath projects 2021
	h0sane on A sort of Polymath on a famous…
	Thomas Vu on Polymath projects 2021

The polymath blog