The polymath blog

After the success of Polymath1 and the launching of Polymath3 and Polymath4, Tim Gowers wrote a blog post “Possible future Polymath projects” for planning the next polymath project on his blog. The post mentioned 9 possible projects. (Four of them later turned  to polymath projects.) Following the post and separate posts describing some of the proposed projects, a few polls were taken and a problem – the Erdős discrepancy problem, was selected for the next project polymath5. In Combinatorics and more I reviewed some of the proposed projects from 2009, and in the same post I briefly and sometimes vaguely discussed the 2021 list, that I plan to present and discuss in detail in the next couple of months.

Is there any polynomials of two variables with rational coefficients, such that the map  is a bijection?  This is a famous 9-years old open question on MathOverflow.  Terry Tao initiated a sort of polymath attempt to solve this problem conditioned on some conjectures from arithmetic algebraic geometry.  This project is based on an plan by Tao for a solution, similar to a 2009 result by Bjorn Poonen who showed that conditioned on the Bombieri-Lang conjecture, there is a polynomial so that the map  is injective. (Poonen’s result  answered a question by Harvey Friedman from the late 20th century, and is related also to a question by Don Zagier.)

The Hadwiger-Nelson problem is that of determining the chromatic number of the plane (), defined as the minimum number of colours that can be assigned to the points of the plane so as to prevent any two points unit distance apart from being the same colour. It was first posed in 1950 and the bounds were rapidly demonstrated, but no further progress has since been made. In a recent preprint, I have now excluded the case by identifying a family of non--colourable finite “unit-distance” graphs, i.e. graphs that can be embedded in the plane with all edges being straight lines of length . However, the smallest such graph that I have so far discovered has [EDIT: after correction] vertices, and its lack of a -colouring requires checking for the nonexistence of a particular category of -colourings of subgraphs of it that have [EDIT: after correction] and vertices, which obviously requires a computer search.

I’m therefore wondering whether a search for “simpler” examples might work as a Polymath project. An example might be defined as simpler if it has fewer vertices, or if it has a smaller largest subgraph whose -colourability must be checked directly, etc. I feel that a number of features make this nice for Polymath:

1. being graph theory, it’s nicely accessible/seductive to non-specialists
2. it entails a rich interaction between theory and computation
3. simpler graphs may lead to insights into what properties such graphs will always/usually have, which might inspire strategies for seeking 6-chromatic examples, improved bounds to the analogous problem in higher dimensions, etc.

I welcome comments!

Aubrey de Grey

This post is to note that the polymath13 project has successfully settled one of the major objective. Reports on it can be found on Gower’s blog especially in this post Intransitive dice IV: first problem more or less solved? and this post Intransitive dice VI: sketch proof of the main conjecture for the balanced-sequences model.

A polymath-style project on non transitive dice (Wikipedea) is now running over Gowers blog. (Here is the link to the first post.)

We haven’t quite hit the 100-comment mark on the second Polymath 12 blog post, but this seems like a good moment to take stock.  The project has lost some of its initial momentum, perhaps because other priorities have intruded into the lives of the main participants (I know that this is true of myself).  However, I don’t want to turn out the lights just yet, because I don’t believe we’re actually stuck.  Let me take this opportunity to describe some of the leads that I think are most promising.

Online Version of Conjecture

For general matroids, the online version of Rota’s Basis Conjecture is false, but it is still interesting to ask how many bases are achievable.  One of the nicest things to come out Polymath 12, in my opinion, has been a partial answer to this question: It is somewhere between n/3 + c and n/2 + c.  There is hope that this gap could be closed.  If the gap can be closed then in my opinion this would be a publishable short paper.  Incidentally, if a paper is published by Polymath 12, what pseudonym should be used?  I know that D. H. J. Polymath was used for the first project, but maybe R. B. C. Polymath would make more sense?

Graphic Matroids

It was suggested early on that graphic matroids might be a more tractable special case.  It wasn’t immediately clear to me at first why, but I understand better now.  Specifically, graphic matroids with no K₄ minor are series-parallel and therefore strongly base-orderable and therefore satisfy Rota’s Basis Conjecture.  Thus, in some sense, K₄ is the only obstruction to Rota’s Basis Conjecture for graphic matroids, whereas the analogous claim for matroids in general does not hold.

In one of my papers I showed, roughly speaking, that if one can prove an n × 2 version of Rota’s Basis Conjecture, then this fact can be parlayed into a proof of the full conjecture. Of course the n × 2 version is false in general, but I do believe that a thorough understanding of what can happen in just two columns will give significant insight into the full conjecture.  One question I raised was whether any n × 2 arrangement of edges can yield two columns that are bases if we pull out no more than n/3 edges. This is perhaps a somewhat clumsy question, but it is trying to get at the question of whether there are any n × 2 counterexamples that are not just the disjoint union of copies of K₄ that have been expanded by “uncontracting” some edges. If we can classify all n × 2 counterexamples then I think that this would be a big step towards proving the full conjecture for graphic matroids.

This is of course not the only possible way to tackle graphic matroids. The main point is that I think there is potential for serious progress on this special case.

Computational Investigations

I mentioned an unpublished manuscript by Michael Cheung that reports that the n = 4 case of Rota’s Basis Conjecture is true for all matroids.  I find this to be an impressive computation and I think it deserves independent verification.

Finding 5 × 2 counterexamples to Rota’s Basis Conjecture would also be illuminating in my opinion. Gordon Royle provided a link to a database of all nine-element matroids that should be helpful. Luke Pebody started down this road but as far as I know has not completed the computation.

Strongly Base-Orderable Matroids

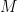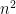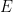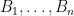In 1995, Marcel Wild proved the following result (“Lemma 6”): Let be a matroid on an -element set that is a disjoint union of independent sets of size . Assume that there exists another matroid 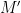on the same ground set 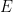with the following properties:

(1) 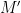is strongly base orderable.

(2) 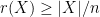for all 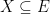, where is the rank function of .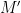

(3) All circuits 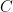of 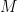satisfying 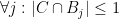remain dependent in .

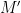Then there is an grid whose 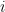th row comprises 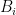and whose columns are independent in .

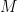Wild obtained several partial results as a corollary of Lemma 6.  How much mileage can we get out of this?  Can we always find a suitable 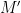for graphic matroids?

Variants and Related Conjectures

I’m less optimistic that these will lead to progress on Rota’s Basis Conjecture itself, but maybe I’m wrong.  Gil Kalai made several suggestions:

1. Consider d + 1 (affinely independent) subsets of size d + 1 of 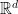such that the origin belongs to the interior of the convex hull of each set. Is it possible to find d + 1 sets of size d + 1 such that each set is a rainbow set and the interior of the convex hulls of all these sets have a point in common?
2. The wide partition conjecture or its generalization to arbitrary partitions.
3. If we have sets B₁, …, B_n (not necessarily bases) that cannot be arranged so that all n columns are bases, then can you always find disjoint n + 1 sets C₁, …, C_n+1 such that each set contains at most one member from each B_j and the intersection of all linear spans of the C_i is non trivial?  (I confess I still don’t see why we should expect this to be true.)

Pavel Paták presented a lemma from one of his papers that might be useful. Let M be a matroid of rank r and let S be a sequence of kr elements from M, split into r subsequences, each of length at most k. Then any largest independent rainbow subsequence of S is a basis of M if and only if there does not exist an integer s < r and set of s + 1 color classes, such that the union of these color classes has rank s.

In a different direction, there are graph-theoretic conjectures such as the Brualdi–Hollingsworth conjecture: If the complete graph K_2m (for m ≥ 3) is edge-colored in such a way that every color class is a perfect matching, then there is a decomposition of the edges into m edge-disjoint rainbow spanning trees.

Remarks on Previous Blog Post

Finally, let me make a few remarks about the directions of research that were suggested in my previous Polymath 12 blog post.  I was initially optimistic about matroids with no small circuits and I still think that they are worth thinking about, but I am now more pessimistic that we can get much mileage out of straightforwardly generalizing the methods of Geelen and Humphries, for reasons that can be found by reading the comments.  Similarly I am more pessimistic now that the algebro-geometric approach will yield anything since being a basis is an open condition rather than a closed condition.

The other leads in that blog post have not been pursued much and I think they are still worth looking at.  In particular, that old standby, the Alon–Tarsi Conjecture, may still admit more partial results. Rebecca Stones’s suggestion that maybe L_n^even – L_n^odd ≢ 0 (mod p) when p = 2n + 1 is prime still looks to me like a good idea and I don’t think many people have seriously thought about this. Also I agree with David Glynn that more people should study Carlos Gamas’s recent paper on the Alon–Tarsi Conjecture.