The Hadwiger-Nelson problem is that of determining the chromatic number of the plane (), defined as the minimum number of colours that can be assigned to the points of the plane so as to prevent any two points unit distance apart from being the same colour. It was first posed in 1950 and the bounds
were rapidly demonstrated, but no further progress has since been made. In a recent preprint, I have now excluded the case
by identifying a family of non-
-colourable finite “unit-distance” graphs, i.e. graphs that can be embedded in the plane with all edges being straight lines of length
. However, the smallest such graph that I have so far discovered has
[EDIT:
after correction] vertices, and its lack of a
-colouring requires checking for the nonexistence of a particular category of
-colourings of subgraphs of it that have
[EDIT:
after correction] and
vertices, which obviously requires a computer search.
I’m therefore wondering whether a search for “simpler” examples might work as a Polymath project. An example might be defined as simpler if it has fewer vertices, or if it has a smaller largest subgraph whose -colourability must be checked directly, etc. I feel that a number of features make this nice for Polymath:
- being graph theory, it’s nicely accessible/seductive to non-specialists
- it entails a rich interaction between theory and computation
- simpler graphs may lead to insights into what properties such graphs will always/usually have, which might inspire strategies for seeking 6-chromatic examples, improved bounds to the analogous problem in higher dimensions, etc.
I welcome comments!
Aubrey de Grey
[…] de Grey have made now a polymath proposal over the polymath blog aimed at finding simpler constructions, namely constructions with a smaller […]
Pingback by Aubrey de Grey: The chromatic number of the plane is at least 5 | Combinatorics and more — April 10, 2018 @ 9:23 am |
Exiting stuff! Indeed it has a very Polymath flavor, so I hope it is accepted soon. I’d definitely contribute what I can…
Comment by Anonymous — April 10, 2018 @ 9:51 am |
Can you make your smallest graph available in any convenient format? (edge lists or in any other form)
Comment by Gordon Royle — April 10, 2018 @ 10:02 am |
I would love to see this as well. For instance, if you are using Mathematica (inferred from your preprint), you could do:
Export[“g.col”, AdjacencyMatrix[g]]
where g is assumed to be the graph.
Comment by Juho — April 10, 2018 @ 1:58 pm |
I just posted a few convenient formats here: http://dustingmixon.wordpress.com/2018/04/10/the-chromatic-number-of-the-plane-is-at-least-5/
Comment by Dustin G. Mixon — April 10, 2018 @ 2:30 pm |
Thanks Dustin and Boris – and even more thanks for checking the chromatic number! Everyone, please note that the graph Dustin checked has 1585 vertices, not 1567, because he used the graph I describe as “Sb” for “Sa”, i.e. he didn’t remove the nine vertices. I have just received a report that the 1567-vertex graph is 4-colorable; Dustin, could you please check it? It would be great to determine ASAP whether I have messed up in the removal of those last nine vertices
Comment by ag24ag24 — April 10, 2018 @ 3:20 pm |
[…] with this property. He concludes with a description of a graph with 1567 vertices. He has since proposed a polymath project to decrease this number even […]
Pingback by The chromatic number of the plane is at least 5 – Short, Fat Matrices — April 10, 2018 @ 2:29 pm |
Update: the smallest case may need to be revised up to 1585 vertices. Many thanks to Brendan McKay and Gordon Royle for letting me know overnight that they had successfully 4-coloured my 1567er; as a result I found a bug in the part of my code that implements the relaxation described in section 5.4 and now it agrees. Mercifully this only means, possibly, that fewer than nine vertices can be removed from S to make Sa; the worst case is that we could remove none, which leaves the full graph with 1585 vertices, and I’m pleased to say that Dustin Mixon and Boris Alexeev have confirmed the non-4-colorability of that graph using a completely different algorithm than mine (a SAT solver):
It will probably take me the rest of the day to determine how many vertices I can in fact remove from S to make Sa; I will post here when I have an answer.
Comment by ag24ag24 — April 10, 2018 @ 8:13 pm |
Given that at least two people have confirmed that the 1585-vertex graph is not 4-colorable with different SAT solvers, the basis seems beyond doubt. So then how is it going to be determined whether or not the proposal is accepted as a polymath project ?
Or can we start putting comments here, however small ?
Comment by Anonymous — April 11, 2018 @ 1:16 pm |
By all means contribute comments (mathematical, organisational, or otherwise) if you are interested in participating; it tends to be pretty clear after a few days of discussion if there is enough of a critical mass of potential active participants to run a full polymath project. Occasionally what happens instead is that there are just two or three people who are seriously interested in pushing things further, and they take things offline to pursue a more traditional collaboration.
Comment by Terence Tao — April 11, 2018 @ 3:58 pm |
Update: after fixing my bug and re-running the code that seeks deletions from Sa, I now find that just two vertices can be deleted wtthout introducing a problematic (as defined in section 5.4) 4-coloring. This therefore leads to a size of 1581 for the full 5-chromatic graph (which contains two copies of Sa). I have just uploaded to the arxiv a revision of my paper (I gather it will go live within a few hours), incorporating this correction as well as making the construction clearer in section 6 (and adding a number of particularly apposite acknowledgements!). Whew! I will now post this update to the slew of other blogs I know of where the topic is being discussed, and I’ll also fix Wikipedia’s page on the H-N problem (I didn’t make the initial edit that reported 1567, but I think speed is of the essence for that).
by way of further fuel for the Polymath idea, I will also reveal that someone has already found a small improvement to my 1581er. I won’t steal thunder by saying any more, but I’ve asked the discoverer to post something here.
I also see that Geoffrey Exoo has now verified my graph M:
and there is another confirmation of the 1585er noted here:
https://mathoverflow.net/questions/236392/has-there-been-a-computer-search-for-a-5-chromatic-unit-distance-graph#297407
Comment by ag24ag24 — April 11, 2018 @ 3:32 pm |
Noam Elkies has independently suggested this same topic for a Polymath project:
https://mathoverflow.net/questions/219638/proposals-for-polymath-projects/297436#297436
Thanks Noam!
Comment by ag24ag24 — April 11, 2018 @ 5:08 pm |
A tiny comment : the smallest euclidean distance between non-neighbours in the 1585-vertex graph is 0.0009975777 (between vertices 1499 and 1537). On the other hand it is 0.7365955 for the Moser spindle.
So, assuming that “nicer” graphs tend to have larger distances between vertices, an idea would be to exclude from the search those graphs that have dist-min < 0.001, on top of the #vertices < 1585 constraint.
Comment by Anonymous — April 11, 2018 @ 7:09 pm |
Typo: I meant to say 0.4574271 for the Moser spindle.
Comment by Anonymous — April 11, 2018 @ 7:13 pm |
Interesting idea! There are three essentially different ways to chain Sb-Sa-Sa-Sb together, differing in whether the rotation associated with each link is clockwise or anticlockwise; can you try all three and let us know this minimum value for the other two cases? Um, also I think it’s actually only 0.4574 for the Moser spindle (the two vertices in its centre).
Comment by ag24ag24 — April 11, 2018 @ 7:22 pm |
Update: We now have a 1577-vertex subgraph of the previous 1585-vertex graph that is also not 4-colorable. This appears to be the minimal 5-chromatic subgraph. More details can be found here:
Comment by Dustin G. Mixon — April 11, 2018 @ 7:25 pm |
Thanks Dustin! Everyone: for the avoidance of doubt, this was the small improvement that I mentioned in my update three hours ago.
Comment by ag24ag24 — April 11, 2018 @ 7:29 pm |
To clarify: the 1581-vertex graph that I now report as the record in my paper is the best that can be done by shrinking Sa. Dustin and Boris, using their much faster code (a SAT solver), were able to check the full graph. Four of their deletions are (necessarily) the same as mine.
Comment by ag24ag24 — April 11, 2018 @ 7:38 pm |
I thought it might be worth formalising a generalisation of my construction, as a seed for possible new constructions that get away from the specifics of spindles and hexagons and so on. Here goes :
We consider three unit-distance graphs H,M,L such that M and L both have at least one induced subgraph identical to H.
Let these sets of subgraphs be P for M and Q for L, and let the set of 4-colourings of H be S. Then we seek H,M,L such that:
– for some subset T of S
– for some member J of P
– for some subset R of Q
– in all 4-colourings of M, the colouring of J is a member of T, and
– in all 4-colourings of L, the colouring of at least one member of R is not a member of T
If we can find such, then we create a graph N by “stamping” {M,J} onto {L,R}: we define this to mean juxtaposing a copy of L and |R| copies of M in such a way that the images of J in the copies of M correspond to the members of R in the copy of L.
Then N is not 4-colourable. For, a putative 4-colouring would need to have the colouring of every member of R be a member of T (since they are the copies of H corresponding to J within the various copies of M), but it would also need the colouring of at least one member of R to be not a member of T (since they are embedded within a copy of L).
Hoping this gives someone some ideas! As things stand I have no idea whether there are other N’s constructible in this way that might have fewer than 20425 vertices, nor (if so) whether they could be shrunk to fewer than 1581, nor whether the component M and L could be smaller than 1345 and 121 respectively … seems like plenty to explore.
Comment by ag24ag24 — April 12, 2018 @ 1:24 am |
Here is a reformulation of this construction that might be helpful:
We seek three graphs A, B, C with fixed unit-distance embeddings in the plane, as well as a predicate “special” that classifies (proper 4-)colorings of A as special or not special, so that
1. A is literally a subset of B.
2. Every proper 4-coloring of B induces a special coloring of A.
3. Every proper 4-coloring of C contains an (isometric) copy of A where the induced coloring is not special.
Then by extending every copy of A in C to a copy of B, we reach the desired conclusion of a unit-distance graph that is not 4-colorable.
Comment by Boris — April 12, 2018 @ 12:42 pm |
So, for example, Hubai and Palvolgyi (in comment 14, below) take A to be the vertices of a 1-sqrt(3)-2 triangle, and they define “special” to be “2-colored.” They presumably found a C such all of its colorings force one such triangle to be 3-colored, but they don’t have a B. It seems that finding B (e.g., Aubrey’s M) is the bottleneck.
Comment by Dustin G. Mixon — April 12, 2018 @ 1:37 pm |
Yep. I think I also got lucky by looking for monochromatic rather than trichromatic triangles.
Comment by ag24ag24 — April 12, 2018 @ 3:06 pm |
Many thanks Boris – conventional mathematical language is not my strong suit, but I’m learning! My construction is slightly more general in that it allows for the possibility that there are some copies of A in C that we can just ignore – your item (3) would then be “There is a set of isometric copies of A in C at least one of which is not-special in every proper 4-colouring of C” – but of course there is nothing to stop us from extending superfluous copies of A, so I like your simplification.
Comment by ag24ag24 — April 12, 2018 @ 3:05 pm |
Essentially, the proof in the paper consists on 2 parts. a) Proof that any proper 4-coloiring of the plane must contain a monochromatic regular triangle with side length \sqrt{3} and b) proof that no proper 4-coloiring can contain such a triangle.
Was there any known results of the form “no proper 4-coloiring can contain a given monochromatic triangle?” (which has no side length 1 otherwise this is trivial)? If we had simple computer-free proof for SOME triangles, we could use it to prove similar result for further triangles, and eventually get a contradiction.
Comment by Bogdan — April 12, 2018 @ 11:05 am |
I’m unaware of any such result; I did think in January about looking for such triangles but I never spent time doing so.
Comment by ag24ag24 — April 12, 2018 @ 3:08 pm |
We (Tamas Hubai and Domotor Palvolgyi) have tried a very similar approach to get a lower bound of 5 about half a year ago. An argument, that is surprisingly similar to the one that can be found in the paper, shows that there’s always a right angle triangle with side lengths (1, sqrt(3), 2) whose 3 vertices have 3 different colors. But we couldn’t reach a contradiction from here, so I think that the most important idea in the paper was to use those “extra Moser spindles” that lead to a 5-chromatic graph from the given configuration. I wonder if adding something similar (or the same thing) can also reach a contradiction from our panchromatic right angle triangle, or if our example was weaker in this sense.
Comment by domotorp — April 12, 2018 @ 11:50 am |
I think it was probably weaker. The line of speculation that I describe at the beginning of section 4 seems only to work because of my use of monochromatic triangles as opposed to panchromatic ones. But I bet there are other ways to build an incompatible pair of graphs L and M in which the nature of the incompatibility is very different from mine.
Comment by ag24ag24 — April 12, 2018 @ 3:25 pm |
Right everyone, I am delighted to report that significant progress has been made in terms of one of the measures of “simplicity” that seem to be of interest here, and indeed the one that most interests Terry. In section 5 I note that the most direct way to shrink N is to shrink M, but actually I never tried doing that, because instead I asked (as soon as I had the 1345er M in hand) the outrageous question of whether that M could itself serve as S, i.e. without assembling 13 copies, and to my great shock it indeed could, i.e. its linking vertices behaved as required. So I skipped the search for shrinkings of M entirely. However, as first noted by Terry, possibly the most mathematically interesting type of shrinkage is of the largest graph whose 4-colourability (perhaps under some criterion of what colourings are permitted) must be directly checked rather than determined by looking at subgraphs of it. In my paper that number is 397, i.e. my Sb, and I was definitely expecting that M could not be shrunk beyond that. However, Marijn Heule now reports that he has shrunk it to 300 vertices – and I bet he’s not done, because his graphs was obtained by greedily removing the vertices in arbitrary order and in the process he loses all symmetry. I have asked him to join this discussion.
Comment by ag24ag24 — April 12, 2018 @ 3:43 pm |
My shrinking procedure works as follows: I encode whether graph M has a 4-coloring such that the subgraph H has a monochromatic triple as a SAT problem. This problem is unsatisfiable. Most SAT solvers support emitting a proof of unsatisfiability. One can extract from the proof the vertices that were involved in the argument that there is no such 4-coloring. I used my tool DRAT-trim for this purpose. In the first step it removes roughly 550 vertices from M (the exact number depends on the random seed). The entire step, i.e. producing the proof and extracting the involved vertices, can be done in about a second. The procedure is repeated using the reduced graph as starting point for the next iteration. When the procedure reaches a fixpoint after some iterations, I started removing individual vertices until a minimal core was found (removing any vertex from the core breaks the property).
Comment by Marijn Heule — April 12, 2018 @ 6:34 pm |
Many thanks Marijn. Do the vertices removed in the first step vary a lot depending on the random seed (just that roughly the same NUMBER of vertices is always used in the proof)? I am wondering about a partitioning of vertices into three sets (always used in, say, 100 runs of the proof; sometimes used; never used). If the “sometimes used” set is small, maybe a smaller set can be found by going exhaustive just with that set. And actually, if that set is large, maybe a neat way forward could be to rank the vertices according to their observed probability of being used in the proof – if you remove them in that order (least likely first, obviously) then maybe you’ll get close to a true minimum more efficiently. Worth a try?
Comment by ag24ag24 — April 12, 2018 @ 6:46 pm |
> the exact number depends on the random seed
Where is the randomness? Is DRAT-trim a randomized algorithm?
Comment by Dustin G. Mixon — April 12, 2018 @ 7:59 pm |
No DRAT-trim is deterministic. I shuffle the order of the clauses before solving the formula. This results in different proofs of unsatisfiability. Without shuffling the procedure results in an early (and poor) fixpoint.
Comment by Marijn Heule — April 12, 2018 @ 8:41 pm |
I think we can decrease the number of copies of H in L that need to be extended to a copy of M (by nearly a factor of 2).
To see this, I will modify the construction of L. Let H1 denote the set of points in the hex lattice of norm at most 1 (i.e., H in Aubrey’s paper). If I were to rotate a second copy of H1 about a=(-1,0) to produce an edge between b=(1,0) and its rotated version b’, then either a and b have different colors, or a and b’ have different colors. As such, at least one of these copies of H1 doesn’t receive the coloring depicted in the bottom-right panel of Figure 1 in Aubrey’s paper.
Now let H2 denote the set of points in the hex lattice of norm at most 2 (this is a subgraph of J in Aubrey’s paper). If the vertices in H1 are colored according to the bottom-left panel of Figure 1, then it is straightforward to show that any coloring of the remainder of H2 that avoids monochromatic sqrt(3)-regular triangles is necessarily of a form depicted in the top row of Aubrey’s Figure 3. If I were to rotate a second copy of H2 about the origin to produce an edge between (2,0) and its rotated version (as well as 5 other edges by symmetry), then one of these copies must fail to match the top row of Figure 3 (indeed, if one of the copies matches, then the other’s “linking vertices” exhibit the wrong pattern of vertex colors relative to the origin’s color).
Overall, we may take K’ to be obtained from two copies of H2 by rotating about the origin and producing 6 extra edges, as above. Next, we may take L’ to come from two copies of K’ by rotating about (-1,0). Indeed, one of these copies of K’ necessarily has its H1 portion colored differently than the bottom-right of Figure 1, and in this copy of K’, one of the copies of H2 fails to match the top row of Figure 3, meaning the H1 portion of this copy of H2 must be colored according to the top row of Figure 1. L’ is composed of 4 copies of H2, each of which is composed of 7 copies of H1, resulting in a total of 28 copies of H1 (almost half of Aubrey’s 52).
Comment by Dustin G. Mixon — April 12, 2018 @ 7:20 pm |
> meaning the H1 portion of this copy of H2 must be colored according to the top row of Figure 1
Rather, *some copy of H1* in this copy of H2 must be colored according to the top row of Figure 1. (It could be that the H1 portion matches the bottom-left of Figure 1, but that a monochromatic sqrt(3)-regular triangle appears elsewhere in this copy of H2.)
Comment by Dustin G. Mixon — April 12, 2018 @ 7:36 pm |
Thanks! Yeah, in a nutshell what I think you are saying is two things:
– that the whole business of linking vertices can be jettisoned, because we create L in a different way (with the two copies of K having relative rotation 2*arcsin(1/4) rather than 2*arcsin(1/8) and having (-1,0) rather than (-2,0) coincident)
– that if we do this, the additional colourings of your H2 (which I think could more naturally be denoted J’) that arise from discarding all the vertices of J that are at sqrt(7) from the origin become irrelevant, because the new construction of L’ still needs at least one of its (now) 28 copies of H to have a monochromatic triple.
Is that a valid restatement of your construction?
Comment by ag24ag24 — April 12, 2018 @ 9:05 pm |
Yes, that looks like an accurate summary.
Comment by Dustin G. Mixon — April 12, 2018 @ 9:09 pm |
After discussing with Aubrey, it seems that the second copy of J’ will need to be all of J just in case its coloring comes from the second row of Figure 3. Still, this reduces the number of copies of H from 52 to 40.
Comment by Dustin G. Mixon — April 12, 2018 @ 10:07 pm |
And the vertex count from 121 to 97. All good! I suspect that a few more vertices (and thus H’s) can go, actually, as a result of the nice fact that your construction introduces three new edges rather than just one at the K-to-L step. I’ll check that later unless someone beats me to it :-)
Comment by ag24ag24 — April 12, 2018 @ 10:12 pm |
Oooh it’s better than that. Since the J-to-K rotation and the K-to-L rotation are now the same angle, we can merge more vertices and get more edges in addition to the three I just mentioned, by being judicious about which rotations are clockwise and which are anticlockwise. Recall that in the paper I had N formed by a chain of four copies of S in the configuration Sb-Sa-Sa-Sb. Let’s use the same notation (I’m gonna drop the primes for now) with the M-less version: Jb-Ja-Ja-Jb. In fact let’s be specific and say Jb1-Ja1-Ja2-Jb2. Now, with the new linkage, let’s say that Ja2 is the original unrotated J. Then let Jb2 be Ja2 rotated anticlockwise about the origin and let Ja1 be Ja2 rotated anticlockwise about (-1,0) – and then let Jb1 be Ja1 rotated clockwise about the rotated version of the origin. Then, bingo, Jb1’s (1,0) is on top of Jb2’s (1,0). I’ll explore this later too.
Comment by ag24ag24 — April 12, 2018 @ 10:44 pm |
The natural next step is presumably to combine Marijn’s improved M with Dustin’s improved L (which has 73 [EDIT: 97] vertices), and then apply the various S-shrinking and N-shrinking methods to the result. Marijn is still getting improvements (he’s at 281 now), so let’s see how low he can go today.
Comment by ag24ag24 — April 12, 2018 @ 9:13 pm |
Some possible modifications of M:
(1) In section 4.2, one may trim W with a radius of sqrt(6+sqrt(33))/3 instead of sqrt(3), which reduces the number of vertices of M from 1345 to 859. This is not an improvement over Marijn’s shrinking result but it might be combined with it.
(2) It is also possible to build M from four copies of W instead of seven, placing them at the centre and every second vertex of the hexagon. In this case we need a somewhat larger radius of (5sqrt(3)+sqrt(11))/6.
(3) Furthermore, in the article we are looking for an M that can’t be 4-coloured in such a way that the central H contains a monochromatic triangle. We can be more specific and select one of the two regular triangles of side length sqrt(3) to be monochromatic. This would allow us to further shrink the size of the graph that needs to be checked programmatically, though the size of the final graph doesn’t decrease as we now need to attach two copies of M to each hexagon in L. I guess this might push Marijn’s current bound further down. It definitely helps in case (2) above, albeit slightly.
Comment by Tamás Hubai — April 13, 2018 @ 11:59 am |
Many thanks Tamas. These are very interesting variations. Marijn’s latest is 278 vertices, but I will suggest that he might apply his shrinking procedure starting with your new M’s instead of mine.
Meanwhile, I am putting together code to check for ways to further simplify Dustin’s improved L. Per my last reply to him above, the choice of clockwise and anticlockwise that I noted ends up making the overall full graph reflectionally symmetrical about two perpendicular lines (this is before we shrink any of the J’s). This not only motivates a translation and rotation to make those lines be the axes; it also shows that there are not three but six edges added by the “K-to-L” step, three each between the Ja’s and between the Jb’s. This might suggest that there are even better ways to shrink the new L than Dustin’s deletion of the outermost 12 vertices from the Ja’s; there are quite a lot of new constraints arising from these additional edges, so we may be able to get down below 40 H’s. One way or another, I think we will now be able to dispense with the analysis of graphs analogous to my J and S and just focus on H, L, M and N.
I’m also implementing a versatile colouring-searcher based on Mathematica’s SAT solver (which I only now know exists – thanks Boris!), that allows for the exclusion of specified colourings of a list of specified subsets of vertices.
Comment by ag24ag24 — April 13, 2018 @ 3:33 pm |
> though the size of the final graph doesn’t decrease as we now need to attach two copies of M to each hexagon in L
In the proof that every coloring of L produces a monochomatic triple, I don’t think we use both triples in every hexagon. This relates to Aubrey’s comment about “superfluous copies of A” to Boris under comment 12 above.
Comment by Dustin G. Mixon — April 13, 2018 @ 4:26 pm |
In other news, discussions are occurring elsewhere regarding two related questions that rank high among those into which I hope that the shrinking we’re exploring here will provide insight: the fractional chromatic number of the plane and the minimum degree of a unit-distance graph (possibly of a given maximum size). I have asked the participants (who in one case include Dustin) to contribute here, but meanwhile please see the more recent comments at:
https://www.scottaaronson.com/blog/?p=3697
Comment by ag24ag24 — April 13, 2018 @ 4:42 pm |
[…] number of the plane is at least 5, as well as some recent progress that has been made on the polymath proposal page and […]
Pingback by The chromatic number of the plane is at least 5, part II – Short, Fat Matrices — April 13, 2018 @ 5:39 pm |
(This blog entry should be helpful to a newcomer to this project. I also discuss a few additional directions to pursue.)
Comment by Dustin G. Mixon — April 13, 2018 @ 5:41 pm |
I have started a wiki page on the PolymathWiki to record all the links and other data for this project: http://michaelnielsen.org/polymath1/index.php?title=Hadwiger-Nelson_problem
Aubrey (or Dustin?), I will need help filling out the table on that page which lists various key graphs in your paper, and updating it also with some of the new graphs in the discussion. Probably the simplest thing to do is to get an account on the wiki so you can edit things directly; you can contact Michael Nielsen about this at mn@michaelnielsen.org . Or you can supply the relevant data to me, say by email, and I can input it by hand.
Comment by Terence Tao — April 13, 2018 @ 8:40 pm |
Awesome – thank you Terry! I am happy to take charge of this page and I will contact Michael now.
Comment by ag24ag24 — April 13, 2018 @ 8:45 pm |
Just an interim report on the new L arising from Dustin’s great idea and my refinement. In its maximal form built from four copies of my original J, it turns out to have only the one merged vertex that I already mentioned, so the vertex count is 120 – but the edge count rises much more than I’d realised, from 301 to 354 (I was expecting only 306). I think I’ll be able to do a exhaustive search for the maximal set of vertices that can be deleted without letting no (remaining) copy of H have a monochromatic triple. Meanwhile I am going to try to include here the picture of the new L, which is much prettier than my original! Hm, OK, I tried and failed to do that. Anyone know how to attach a file?
Comment by ag24ag24 — April 14, 2018 @ 2:28 am |
Dear Aubrey,
If you email me the file I can host it on this blog and add the link; otherwise you can host it on another web site and give the link here. I don’t think there is a facility to directly upload images into a comment though.
Comment by Terence Tao — April 14, 2018 @ 2:53 pm |
Many thanks Terry – but it’s OK – Dustin is setting up a dropbox for this purpose for the polymath project which should be active very shortly, so Ill stick it (and a bunch of other files) there.
Comment by ag24ag24 — April 14, 2018 @ 2:58 pm |
I was able to compute a unit-distance graph with chromatic number 5 with 874 vertices and 4461 edges. The graph is available here:
* http://www.cs.utexas.edu/~marijn/CNP/874.vtx
* http://www.cs.utexas.edu/~marijn/CNP/874.edge
The first file lists the vertices in the format of Mathematica, while the second file shows the graph as list of edges in the DIMACS format.
I observed that the following graph has chromatic number 5: Start with two copies of graph M (or the reduced M mentioned in Tamás Hubai’s post) and let’s call them M1 and M2. Rotate M2 using point {1,0} as center such that the distance between point {-1,0} in M1 and the corresponding point in M2 is 1. The 874-vertex graph is a subgraph of M1 + M2. I used SAT solving techniques based on proofs of unsatisfiability for the reduction. As mentioned in an earlier post, this progress can be randomized. Smaller graphs can probably be obtained by performing multiple such random probes.
Comment by Marijn Heule — April 14, 2018 @ 5:07 pm |
Wonderful! Congratulations Marijn! I thought Dustin’s improvement of 52 to 40 was cool, but I think it’s fair to say that 2 is cooler :-)
I wonder if we can now figure out a computer-free argument for why it works. What is the required property of M that makes this particular “spindling” of two copies of it 5-chromatic?
I think this is the decisive demonstration that our efforts here constitute a useful project. Which is timely, because yesterday Terry made the final decision to use it as Polymath 16. The project will officially be overseen by me and Dustin, and we’re just getting the relevant pages together before making the announcement. There may be a slight delay because we’re both on the road, but watch this space as they say.
Comment by ag24ag24 — April 14, 2018 @ 5:40 pm |
It is interesting (but perhaps known) to understand the situation for construvtions relevant for the Erdos unit distance problems. Famousely Erdos found a unit distance graph on vertices with
vertices with  edges. The construction is (to the best of my memory) by looking at points
edges. The construction is (to the best of my memory) by looking at points  and choosing as edges the distance which occur most number of times. (I suppose the distance is some constant times
and choosing as edges the distance which occur most number of times. (I suppose the distance is some constant times 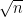 .) Here are some questions:
.) Here are some questions:
1) What is the chromatic number of this construction?
2) Does this graph contains a Moser spindle? Maybe there is a related lattice-based graph with many Moser spindles?
3) Looking at Aubrey’s construction we may think that perhaps basing a similar construction on an Hexagonal lattice may have some advantages.
4) (rather wild) What can be said on the appearance of the most popular distance in an arrangement of points of the Penrose tiling?
5) Is there a “universal” unit distance graph (namely a unit distance graphs containing all small unit-distance graphs) ?
Comment by Gil Kalai — April 14, 2018 @ 5:11 pm |
Regarding question (1), I can establish an upper bound for the chromatic number of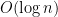 .
.
Proof: Let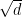 be the distance which appears most often, and let
be the distance which appears most often, and let  be the first prime which is
be the first prime which is 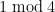 and does NOT divide
and does NOT divide  . Choose a Gaussian prime
. Choose a Gaussian prime 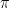 with norm
with norm  and color the square grid modulo
and color the square grid modulo 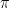 . To see that this is a coloring, note that, if
. To see that this is a coloring, note that, if 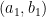 and
and 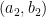 have distance
have distance 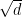 , then
, then 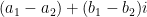 has norm
has norm  and thus cannot be divisible by
and thus cannot be divisible by 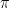 . Since the product of primes up to
. Since the product of primes up to  which are
which are  is roughly
is roughly  , we have
, we have  .
. 
Comment by David Speyer — April 14, 2018 @ 11:42 pm |
But isn’t the chromatic number at most 7, ince it’s a “unit”-distance graph?
Comment by Boris — April 15, 2018 @ 2:46 am |
Whoops! Of course, Boris is right.
Comment by David Speyer — April 15, 2018 @ 1:29 pm |
Okay, let me try to redeem myself. I claim that Erdos’s example is actually bipartite. Let’s join any pair of edges which differ by an integer vector of length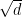 . Let $d = 2^k m$ with $m$ odd. Then, if
. Let $d = 2^k m$ with $m$ odd. Then, if 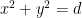 then
then 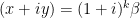 for some algebraic integer
for some algebraic integer 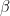 of norm
of norm  . First of all, this means that all edges join vertices in the same coset modulo
. First of all, this means that all edges join vertices in the same coset modulo ![(1+i)^k \mathbb{Z}[i]](https://s0.wp.com/latex.php?latex=%281%2Bi%29%5Ek+%5Cmathbb%7BZ%7D%5Bi%5D&bg=ffffff&fg=000000&s=0&c=20201002) . So we may pass to connected components and work on one coset, which is equivalent to working in the lattice
. So we may pass to connected components and work on one coset, which is equivalent to working in the lattice ![\mathbb{Z}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5Bi%5D&bg=ffffff&fg=000000&s=0&c=20201002) and joining vertices which differ by vectors of length
and joining vertices which differ by vectors of length 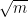 .
.
Now color![\mathbb{Z}[i]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5Bi%5D&bg=ffffff&fg=000000&s=0&c=20201002) in the standard checkerboard coloring, i.e., modulo
in the standard checkerboard coloring, i.e., modulo  .
. 
The analogous argument works to show that Erdos’s construction on the triangular lattice is tripartite (factor out powers of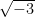 ). It seems to me, though, that it might be worth experimenting with a field where
). It seems to me, though, that it might be worth experimenting with a field where  and
and  both split, though. I think the first such is
both split, though. I think the first such is ![\mathbb{Z}[(1+\sqrt{-23})/2]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BZ%7D%5B%281%2B%5Csqrt%7B-23%7D%29%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Comment by David Speyer — April 15, 2018 @ 4:34 pm |
This is a lovely argument, David. Of course, the hexagonal based coloring shows that the graph is indeed 7-colorable. I wonder does this graph contain triangles? Odd cycles? Moser spindles? Perhaps one can present it, and determine its chromatic number for small values of n?
Comment by Gil Kalai — April 15, 2018 @ 4:51 am |
Very interesting Gil! For sure we want the Polymath project to explore all such questions. Another one that has already come up is whether Cranston and Rabern’s lower bound of 105/29 on the fractional chromatic number of a unit-distance graph can be improved via these approaches.
Comment by ag24ag24 — April 14, 2018 @ 5:43 pm |
[…] of the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, first thread: Simplifying de Grey’s graph – Short, Fat Matrices — April 14, 2018 @ 6:09 pm |
We just launched Polymath16!
From now on, we will use this thread to discuss non-research items that are related to this Polymath project. For research items, the first thread can be found here:
Comment by Dustin G. Mixon — April 14, 2018 @ 6:13 pm |
Thanks Dustin!
Marijn: I think it would be fitting if you could re-post your new discovery on the new thread, as a way to christen it with maximum impact. OK?
Comment by ag24ag24 — April 14, 2018 @ 6:15 pm |
Dustin, one feature that could be useful to turn on on your blog would be to have people see the new comments and commentators (like on this blog and mine).
Comment by Gil Kalai — April 14, 2018 @ 6:30 pm |
[…] needed to verify the proof; already a number of such reductions have been found. See also this blog post where the polymath project was proposed, as well as the wiki page for the project. Non-technical discussion of the project […]
Pingback by Polymath16 now launched: simplifying the lower bound argument for the Hadwiger-Nelson problem | What's new — April 14, 2018 @ 7:04 pm |
The wiki page on notable unit distance graphs is missing another 4-chromatic unit distance graph: the 10-vertex Golomb graph, https://commons.wikimedia.org/wiki/File:GolombGraphProperties.svg
Its greater symmetry compared to the Moser spindle might make it useful in place of the spindle, despite its larger number of vertices.
Comment by eppstein — April 14, 2018 @ 7:26 pm |
Added, thanks.
Comment by Dustin G. Mixon — April 14, 2018 @ 9:21 pm |
I just have a question about unit distance graphs: Is it true that for any finite unit distance graph G there exists a unit distance graph G’, which is isomorphic to G, but vertices of G’ are in A^2, i.e. coordinates are algebraic numbers. What I am trying to ask is: is it true that if we look for an example of a unit distance graph satisfying a certain property (say chromatic number number is 5), then there would be an example with points lying in a certain countable set.
Comment by ivanborsenco — April 15, 2018 @ 2:04 am |
Yes.
Comment by Boris — April 15, 2018 @ 2:50 am |
Everyone: please be sure to use the new page for any technical contributions. Even if you are making a reply to something on this page, the best option is to post it standalone at the new page and post a reply here that only points to that.
Comment by ag24ag24 — April 15, 2018 @ 5:05 am |
Is the research thread the proper place for posting a tentative approach to the maximum density of unit distance graphs problem, or is that too far from the specific goals of this project?
Comment by dsp — April 16, 2018 @ 2:16 pm |
Presumably, examples of high-density unit-distance graphs would be useful to our search for good L and M. With this perspective, I’d say it’s close enough for now.
Comment by Dustin G. Mixon — April 16, 2018 @ 2:29 pm |
[…] the wake of this announcement, a 16th Polymath project has been proposed to try to find a simpler graph, and improve on this result – some have conjectured it might […]
Pingback by The chromatic number of the plane is at least 5 | The Aperiodical — April 17, 2018 @ 7:38 am |
[…] graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of […]
Pingback by Decades-Old Graph Problem Yields to Amateur Mathematician | Unhinged Group — April 17, 2018 @ 4:49 pm |
[…] On Saturday, Marijn Heule, a computer scientist at the University of Texas, Austin, found one with just 874 vertices. Yesterday he lowered this number to 826 […]
Pingback by Decades-Old Graph Problem Yields to Amateur Mathematician | Unhinged Group — April 17, 2018 @ 4:53 pm |
[…] за этим ди Грей опубликовал новую задачу на сайте проекта Polymath Projects по поиску […]
Pingback by Раскраска для математиков | Все о науке — April 17, 2018 @ 8:41 pm |
Distances in a rigid unit-distance graph in the plane – Hiroshi Maehara.
https://www.sciencedirect.com/science/article/pii/0166218X9190070D
Saw this subsequent to AdeG’s paper.
Comment by Michael Ruxton — April 17, 2018 @ 10:15 pm |
I wonder if all possible 5-colourings of the original and newly constructed graphs can be classified in a certain way? As far as I understand the fact that the original Aubrey de Grey’s verification algorithm for 4-colourings terminates rather quickly indicates that the total number of colourings is not very large? It would be of course desirable then to find subgraphs which are forced to be coloured in a small possible number of ways (modulo obvious symmetries), like the hegaxon for the case of four colours.
Comment by Dmitry Zhelezov — April 18, 2018 @ 4:59 pm |
[…] graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of […]
Pingback by Decades-Old Graph Problem Yields to Amateur Mathematician – ESIST — April 19, 2018 @ 1:31 am |
[…] de Grey minimised his five-colour graph to 1,581 vertices, and along with sharing his new work, invited other mathematicians to see if they could improve upon this further, by finding graphs with even fewer points that […]
Pingback by An amateur solved a 60-year-old maths problem about colours that can never touch - Science Global News — April 19, 2018 @ 9:04 am |
[…] de Grey minimised his five-colour graph to 1,581 vertices, and along with sharing his new work, invited other mathematicians to see if they could improve upon this further, by finding graphs with even fewer points that […]
Pingback by An amateur solved a 60-year-old maths problem about colours that can never touch - Science News Hub — April 20, 2018 @ 12:25 am |
[…] de Grey minimised his five-colour graph to 1,581 vertices, and along with sharing his new work, invited other mathematicians to see if they could improve upon this further, by finding graphs with even fewer points that […]
Pingback by An amateur solved a 60-year-old maths problem about colours that can never touch - Science News — April 20, 2018 @ 6:58 am |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, second thread: What does it take to be 5-chromatic? – Short, Fat Matrices — April 22, 2018 @ 1:13 pm |
[…] chromatic number 4. The proof, like the proof of the Four Color Theorem, is computer-assisted. Work on the joint computing project Polymath has reduced the size of the obstruction graph to 874 […]
Pingback by Coloring the plane – The Intrepid Mathematician — April 25, 2018 @ 12:50 pm |
A more general question. Can we prove that in the hexagonal tiling the smallest number of colours such that any two points at a distance slightly larger than a tile diameter are coloured differently is 7?
Comment by Ruggero Gabbrielli — April 26, 2018 @ 10:54 am |
That is easy: If you look at a single hexagon and its six neighbours, their colors must be pairwise distinct.
Comment by Bertram Felgenhauer — April 28, 2018 @ 9:12 am |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, third thread: Is 6-chromatic within reach? – Short, Fat Matrices — May 1, 2018 @ 5:19 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, fourth thread: Applying the probabilistic method – Short, Fat Matrices — May 5, 2018 @ 1:43 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, fifth thread: Human-verifiable proofs – Short, Fat Matrices — May 10, 2018 @ 10:53 am |
[…] graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of […]
Pingback by An Anti-Aging Pundit Solves a Decades-Old Math Problem — May 14, 2018 @ 6:05 am |
[…] graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of […]
Pingback by An Anti-Aging Pundit Solves a Decades-Old Math Problem (From Wired) | Jeremiadus — May 17, 2018 @ 9:54 pm |
[…] se ha conseguido rebajar la configuración hasta los 633 vértices, a través de un proyecto de Polymath (proyectos colaborativos en los que trabajan cientos de matemáticos a través de una […]
Pingback by Un aficionado hace el primer avance de los últimos 60 años en un famoso problema de combinatoria – Noticias — May 18, 2018 @ 4:20 am |
[…] los últimos días se ha conseguido rebajar la configuración hasta los 633 vértices, a través de un proyecto de Polymath (proyectos colaborativos en los que trabajan cientos de matemáticos a través de una página web), […]
Pingback by Un aficionado hace el primer avance de los últimos 60 años en un famoso problema de combinatoria | Ciencia – Noticias.Network — May 23, 2018 @ 4:40 am |
[…] order to simplify the arguments, there was a polymath proposal (link). The corresponding wiki-page is here and it seems that they managed already to find a […]
Pingback by Chromatic Number of the Plane is at least 5 – SPP 2026 — May 23, 2018 @ 11:34 am |
[…] graph to Terence Tao, a mathematician at the University of California, Los Angeles, as a potential Polymath problem. Polymath began about 10 years ago when Timothy Gowers, a mathematician at the University of […]
Pingback by An Anti-Aging Pundit Solves a Decades-Old Math Problem – Collection Geeks — May 26, 2018 @ 9:47 am |
[…] últimos días se ha conseguido rebajar la configuración hasta los 633 vértices, a través de un proyecto de Polymath(proyectos colaborativos en los que trabajan cientos de matemáticos a través de una página web), […]
Pingback by Un aficionado hace el primer avance de los últimos 60 años en un famoso problema de combinatoria – ¡¡Aprendiendo por el mundo!! — May 27, 2018 @ 5:13 pm |
[…] On Saturday, Marijn Heule, a computer scientist at the University of Texas, Austin, found one with just 874 vertices. Yesterday he lowered this number to 826 […]
Pingback by An Anti-Aging Pundit Solves a Decades-Old Math Problem — May 28, 2018 @ 8:35 am |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, sixth thread: Wrestling with infinite graphs – Short, Fat Matrices — May 29, 2018 @ 6:58 pm |
Reblogged this on Artificial Intelligence Research Blog.
Comment by dendisuhubdy — June 14, 2018 @ 2:13 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, seventh thread: Upper bounds – Short, Fat Matrices — June 16, 2018 @ 2:18 pm |
[…] has re-energized the mathematical community around the problem of coloring the plane. A collaborative online effort quickly sprang up to verify de Grey’s graph and find simpler versions (there are now examples […]
Pingback by Four Is Not Enough | Unhinged Group — June 18, 2018 @ 3:26 pm |
[…] has re-energized the mathematical community around the problem of coloring the plane. A collaborative online effort quickly sprang up to verify de Grey’s graph and find simpler versions (there are now examples […]
Pingback by BrokenPla.net - The Important Eclectic News Syndicate — June 18, 2018 @ 10:56 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, eighth thread: More upper bounds – Short, Fat Matrices — June 24, 2018 @ 11:10 am |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, ninth thread: Searching for a 6-coloring – Short, Fat Matrices — July 2, 2018 @ 1:01 pm |
[…] has re-energized the mathematical community around the problem of coloring the plane. A collaborative online effort quickly sprang up to verify de Grey’s graph and find simpler versions (there are now examples […]
Pingback by Four Is Not Enough – شناخت پژوه — July 8, 2018 @ 7:23 am |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, tenth thread: Open SAT instances – Short, Fat Matrices — August 28, 2018 @ 3:03 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, eleventh thread: Chromatic numbers of planar sets – Short, Fat Matrices — September 14, 2018 @ 5:08 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, twelfth thread: Year in review and future plans – Short, Fat Matrices — March 23, 2019 @ 2:01 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, thirteenth thread: Bumping the deadline? – Short, Fat Matrices — July 8, 2019 @ 6:16 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, fourteenth thread: Automated graph minimization? – Short, Fat Matrices — August 5, 2019 @ 12:47 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, fifteenth thread: Writing the paper and chasing down loose ends – Short, Fat Matrices — December 12, 2019 @ 6:29 pm |
[…] the plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, sixteenth thread: Writing the paper and chasing down loose ends, II – Short, Fat Matrices — May 11, 2020 @ 8:50 pm |
The counter example for the case CNP = 4 is like everyone beleives is quite a breakthrough. Maybe a similar attempt for the can rule out 5 and 6 as options for CNP finally proving the conjecture and I think that is a better problem to work on.
Comment by Sai Gopal — October 20, 2020 @ 5:45 pm |
[…] plane is at least 5. Discussion of the project of a non-research nature should continue in the Polymath proposal page. We will summarize progress on the Polymath wiki […]
Pingback by Polymath16, seventeenth thread: Declaring victory – Short, Fat Matrices — February 1, 2021 @ 5:21 am |