This post tentatively kicks off Polymath 12 on Rota’s basis conjecture.
I proposed Rota’s basis conjecture as a possible Polymath project on MathOverflow last year. If you have not read my proposal, I strongly recommend that you read it now, because in it, I sketched some reasons why I thought this would make a good Polymath project, as well as some known partial results and potential avenues for progress.
Recently, I emailed several likely participants, and a number of them responded enthusiastically, enough in my opinion to warrant an attempt to start a Polymath project. I have discussed the possibility with the polymath blog admins and since I do not have a blog of my own, they have generously agreed to host the project here on the polymath blog itself. This means that you should comment freely in the comments section below.
Rota’s basis conjecture states that if B1, B2, …, Bn are n bases of an n-dimensional vector space V (not necessarily distinct or disjoint), then there exists an n × n grid of vectors (vij) such that
1. the n vectors in row i are the members of the ith basis Bi (in some order), and
2. in each column of the matrix, the n vectors in that column form a basis of V.
If this project gets enough momentum to be formally declared “Polymath 12” then it will be important to give a thorough summary of what is already known, and to lay out in some detail all the promising directions. However, at this early stage, I think that it is important to have some “quick wins” to get things moving, so I would like to present a couple of new ideas that I think could lead to some new partial results quickly, and also invite others to present their own ideas.
Idea 1
The first idea is to extend an old result of Aharoni and Berger that I think has not received too much attention from others. Suppose we have two matroids on the same ground set E. By definition, a common independent set is a subset of E that is independent in both matroids. We can try to partition E into a disjoint union of common independent sets, and can ask the question, what is the smallest number β of common independent sets that we need?
Here is the relation to Rota’s basis conjecture. The ground set E has n2 elements, and one of the matroids is defined by the given set of n2 vectors (here, if the same vector appears in more than one basis, we treat the different occurrences as being distinct). The second matroid is the so-called transversal matroid whose independent sets are precisely those subsets of E that contain at most one element from each Bi. From this point of view, Rota’s basis conjecture says that β = n, i.e., that E may be partitioned into n disjoint common independent sets (each necessarily of size n).
Aharoni and Berger have proved a general theorem about matroids that implies, in the specific case of Rota’s basis conjecture, that β ≤ 2n. They also have a very general conjecture on matroids that would imply that β ≤ n + 1 for Rota’s basis conjecture.
Let me now make the simple observation that it is easy to prove directly that β ≤ 2n – 1 for Rota’s basis conjecture. We begin with a lemma. Suppose we have a matroid and suppose that I1, …, In are independent sets with |Ii| = i for all i. Call this a triangular system. Then I claim that there exists a way of choosing a vi from each Ii in such a way that J1 := {vi} is independent. The proof is easy: We start with the forced choice v1 ∈ I1, and then note that by the independent set axiom, since |I2| = 2, there must exist some v2 ∈ I2 that can be added to v1 to produce an independent set of size 2. Similarly, once v1 and v2 are chosen, it follows directly from the independent set axiom that we can add some v3 ∈ I3, and so on. This proves the lemma. Now, once J1 has been constructed, we can imagine removing the elements of J1 from the original triangular system to obtain a smaller triangular system. We can then repeat the argument on this smaller system to form an independent set J2 that contains exactly one element from each Ii for i = 2, 3, …, n. This shows that the original triangular system can be partitioned into (at most) n common independent sets (where as before, the second matroid is the natural transversal matroid).
Returning to the setup for Rota’s basis conjecture, we can write out the n2 given vectors in a grid with the elements of Bi in row i (not worrying about whether the columns are bases) and draw a diagonal to split the bases into two disjoint triangular systems, one of size n and one of size n – 1. So we can partition the vectors into at most n + (n – 1) = 2n – 1 common independent sets, Q.E.D.
So the first question, which I don’t think has been looked at much and which hopefully should not be too hard, is:
Can we show that β ≤ 2n – 2?
Idea 2
In one of my papers I introduced the idea of looking for certain kinds of obstructions to an inductive proof of the conjecture. Specifically, suppose that instead of n bases, we are given n independent sets I1, …, In, each of size k < n. Suppose further that these nk vectors (counted with multiplicity) can be partitioned into k bases somehow (but not necessarily bases that contain exactly one vector from each row). Then we can ask if there exists an n × k grid whose ith row comprises the elements of Ii and whose columns are all bases. In general, the answer will be no, but it is not so easy to come up with counterexamples. I came up with two counterexamples with k = 2, but I think it would be worth doing a computational search for more examples. Even k = 2 and n = 5 has not been checked, as far as I know. If there are not many counterexamples then there is some hope that we could classify them all, and I think that this would be a big step towards proving the full conjecture. Note: one family of counterexamples has been identified by Harvey, Kiraly, and Lau.
Idea 3
The last idea I want to present here is very vague. It is inspired by a paper by Ellenberg and Erman that I recently learned about. The result of the paper itself isn’t relevant, but I thought that the method might be. Roughly speaking, they reduce a certain combinatorial problem involving points and lines in a vector space to a “degenerate” case that is more tractable. Since various “degenerate” cases of Rota’s basis conjecture are known, perhaps the same idea could be applied to extend those degenerate cases to more cases.
As an example of a known degenerate case, let us first generalize Rota’s basis conjecture slightly as follows. Let us allow the vector space V to have some dimension d > n, and instead of n bases, let us take any n independent sets I1, …, In, each of size n. Then we ask for the usual n × n grid except now we only require the columns to be independent and not necessarily bases. As far as I know, there is no known counterexample to this stronger conjecture. Moreover, this stronger conjecture is known to be true if we fix a single, standard basis B of V and insist that every Ii be a subset of B. Two proofs of this fact may be found in Section 2 of this paper.
Let me end this initial blog post here, with just one further comment that a couple of people that I have communicated with recently have some other concrete ideas that we can sink our teeth into immediately. I am going to invite them to explain those ideas in the comments to this blog post.
Congratulation, Tim, for launching polymath12. This is indeed a fascinating question. Let me refer everybody also to Tim’s answer to the polymath question where he proposed this polymath project http://mathoverflow.net/a/231153/1532 .
It contains additional useful information and, in particular, mentions the relation with Alon and Tarsi conjecture on even and odd Latin squares.
Comment by Gil Kalai — February 24, 2017 @ 5:45 am |
This looks interesting! In the spirit of polymath projects where even tiny comments are allowed, and just to check my understanding, would you agree that the problem can be reformulated as : Show that for any the following game has a winning strategy.
the following game has a winning strategy.
a) Pick any bases
bases 
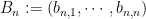
b) Place them along the diagonal of an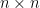 grid :
grid : 
c) move sideways the elements of each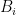 to other cells so that only one element remains in each cell
to other cells so that only one element remains in each cell
d) now for each column of the grid gather all its vectors :
vectors :
e) the game is won if all sets
sets 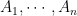 are bases
are bases
Comment by Thomas Sauvaget — February 24, 2017 @ 8:22 am |
The indices I’ve used should be different of course, i.e.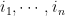 for the first row, then
for the first row, then  for the second, … So maybe it would be even cleaner to write as
for the second, … So maybe it would be even cleaner to write as  for some permutations
for some permutations  . Sorry for these trivialities.
. Sorry for these trivialities.
Comment by Thomas Sauvaget — February 24, 2017 @ 10:04 am |
Yes, this is correct.
Comment by tchow8 — February 24, 2017 @ 4:02 pm |
Thanks for organizing this. I’m coming at this problem from the Alon-Tarsi Conjecture. In “Formulae for the Alon-Tarsi Conjecture” (http://dx.doi.org/10.1137/110797540), I stumbled upon a slick formula:
where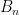 is the set of
is the set of 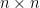
 -matrices and
-matrices and  is the number of copies of
is the number of copies of 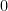 in
in  .
.
I used this formula to give another proof of the Alon-Tarsi Conjecture when n=p-1 and p is an odd prime [Glynn was first], showing that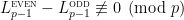 .
.
In “How not to prove the Alon-Tarsi conjecture” with Wanless 2012 (http://projecteuclid.org/euclid.nmj/1330611000), we proved that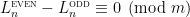 for most small
for most small  , which is an obstacle to re-using this method to prove cases of the Alon-Tarsi Conjecture.
, which is an obstacle to re-using this method to prove cases of the Alon-Tarsi Conjecture.
However, it does not exclude the case: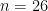 (the smallest $n$ for which the Alon-Tarsi Conjecture is unproved) working modulo
(the smallest $n$ for which the Alon-Tarsi Conjecture is unproved) working modulo 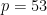 . I choose
. I choose 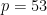 since powers of
since powers of  (such as
(such as  in the above formula) are always congruent to
in the above formula) are always congruent to 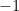 ,
, 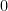 , or
, or 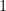 modulo
modulo 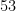 , which I’m hoping can be used to simplify the above sum.
, which I’m hoping can be used to simplify the above sum.
This is where you guys chime in… and hopefully figure out how to simplify this equation (and hopefully identify a non-zero congruence modulo 53, thereby proving the n=26 case of the Alon-Tarsi Conjecture).
Comment by rebeccastones82 — February 24, 2017 @ 12:54 pm |
It seems I need to learn how to use math markup on this site… (?)
Comment by rebeccastones82 — February 24, 2017 @ 1:00 pm |
Dear Rebecca, thanks for the comment. to make a latex formula you need to put between the two dollar signs the word latex and then the formula. For example if I put between dollar signs latex \int_0^1 \Psi(x)dx you get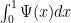
Comment by Gil Kalai — February 24, 2017 @ 1:16 pm |
Can you please explain in more detail which pairs besides (26,53) are potentially amenable to this approach?
pairs besides (26,53) are potentially amenable to this approach?
Comment by tchow8 — February 26, 2017 @ 9:54 pm |
Suppose we want to prove the Alon-Tarsi Conjecture for some even , i.e., we want to show
, i.e., we want to show  . A natural approach is to prove
. A natural approach is to prove 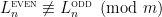 for some
for some  . This approach has worked twice thus far:
. This approach has worked twice thus far:
(a) Drisko proved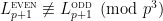 for odd prime
for odd prime  .
.
(b) Glynn proved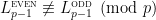 for odd prime
for odd prime  .
.
The problem is: given , what modulus
, what modulus  should we choose? We might as well choose the modulus
should we choose? We might as well choose the modulus  as a prime power (by the Chinese Remainder Theorem).
as a prime power (by the Chinese Remainder Theorem).
In “How not to prove the Alon-Tarsi Conjecture”, we showed that for , we can only have
, we can only have 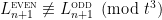 only if
only if 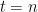 and
and  is an odd prime (and Drisko’s congruence is this exception).
is an odd prime (and Drisko’s congruence is this exception).
The smallest unresolved case of the Alon-Tarsi Conjecture is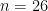 , and in this case we have
, and in this case we have  . So we either work modulo
. So we either work modulo  where
where
(a)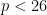 , in which case we need to choose
, in which case we need to choose  so that
so that  is at least 2187,
is at least 2187,
(b) , where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).
, where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).
So, which prime should we choose? If we choose the prime
should we choose? If we choose the prime 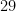 , then
, then  can take on the values
can take on the values 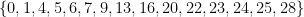 modulo
modulo 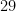 , which makes simplifying the formula for
, which makes simplifying the formula for 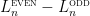 problematic. If we choose the prime
problematic. If we choose the prime 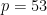 , then
, then  can take on the values
can take on the values  modulo
modulo 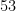 . In this case, we have the property that
. In this case, we have the property that  is the Legendre symbol
is the Legendre symbol  (using the
(using the 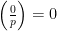 version), so we have
version), so we have
———————————————————————
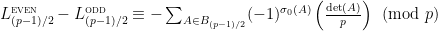
———————————————————————
for any odd prime .
.
It’s possible that this formula might be able to be simplified through elementary number theory.
Comment by rebeccastones82 — February 28, 2017 @ 9:13 am |
Thanks! Is it possible for me to edit too? This line is wrong too (I think it was a copy/paste error), so it won’t make sense:
“(a) , where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).”
, where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).”
It should say:
“(a) , where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).”
, where the above obstacle does not enter into things, which seems easier (it might not be; it’s a guess).”
Comment by rebeccastones82 — February 28, 2017 @ 11:40 am |
Hmm.. this is not displaying correctly either. Hopefully whoever reads the above can figure out what it should say. *shrugs*
Comment by rebeccastones82 — February 28, 2017 @ 11:44 am |
Thanks for this clear explanation. If I understand correctly, this line of thinking could potentially apply to any even such that
such that 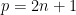 is prime, so in particular we could take
is prime, so in particular we could take 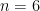 and work mod
and work mod 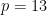 , or we could take
, or we could take  and work mod
and work mod  . In both of these cases, we have the property that
. In both of these cases, we have the property that  can only take on the values
can only take on the values  modulo
modulo  . I mention this because even though the Alon-Tarsi conjecture is known for
. I mention this because even though the Alon-Tarsi conjecture is known for 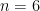 and
and  , these values of
, these values of  are small enough that we may be able to get some intuition for what is going on by direct computation.
are small enough that we may be able to get some intuition for what is going on by direct computation.
For example, by using the table of values in Drisko’s 1998 Electronic J. Combin. paper, I find that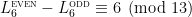 and
and  . In particular, these values aren’t zero, so that’s encouraging! The natural game to play now would be to try to find groups of matrices that cancel each other out modulo
. In particular, these values aren’t zero, so that’s encouraging! The natural game to play now would be to try to find groups of matrices that cancel each other out modulo  , and figure out what’s left over.
, and figure out what’s left over.
Comment by tchow8 — March 2, 2017 @ 10:45 pm |
Here is a calculation that I think would be worth doing. Let denote the set of all
denote the set of all 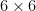 zero-one matrices that are nonsingular over
zero-one matrices that are nonsingular over  and whose rows are in lexicographical order. Compute, for all
and whose rows are in lexicographical order. Compute, for all  and
and 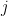 , the number
, the number  of matrices
of matrices  with
with  zero entries and determinant
zero entries and determinant 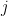 (modulo 13). Since
(modulo 13). Since 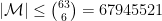 , this is not that large a computation. If we are lucky, there will be patterns in the number
, this is not that large a computation. If we are lucky, there will be patterns in the number  that will suggest how to proceed.
that will suggest how to proceed.
Comment by tchow8 — March 3, 2017 @ 2:57 am |
(-9, 13): 90
(-9, 14): 93
(-9, 15): 180
(-9, 17): 180
(-9, 18): 196
(-8, 11): 32
(-8, 12): 5
(-8, 13): 366
(-8, 14): 1084
(-8, 15): 1148
(-8, 16): 2149
(-8, 17): 1266
(-8, 18): 450
(-8, 19): 450
(-8, 20): 45
(-7, 9): 10
(-7, 12): 558
(-7, 13): 285
(-7, 14): 724
(-7, 15): 1632
(-7, 16): 1542
(-7, 17): 1890
(-7, 18): 1554
(-7, 19): 426
(-7, 20): 360
(-6, 10): 184
(-6, 11): 424
(-6, 12): 1204
(-6, 13): 3104
(-6, 14): 5972
(-6, 15): 11782
(-6, 16): 12088
(-6, 17): 12580
(-6, 18): 9684
(-6, 19): 5572
(-6, 20): 1684
(-6, 21): 540
(-5, 6): 1
(-5, 10): 153
(-5, 11): 1200
(-5, 12): 1326
(-5, 13): 5414
(-5, 14): 7726
(-5, 15): 10128
(-5, 16): 16816
(-5, 17): 16640
(-5, 18): 13625
(-5, 19): 8658
(-5, 20): 4674
(-5, 21): 1815
(-5, 22): 273
(-4, 7): 21
(-4, 8): 64
(-4, 9): 188
(-4, 10): 126
(-4, 11): 1670
(-4, 12): 11181
(-4, 13): 25356
(-4, 14): 54138
(-4, 15): 77482
(-4, 16): 105567
(-4, 17): 104552
(-4, 18): 90642
(-4, 19): 60144
(-4, 20): 34611
(-4, 21): 11516
(-4, 22): 4126
(-4, 23): 379
(-4, 24): 5
(-3, 8): 182
(-3, 9): 1036
(-3, 10): 4182
(-3, 11): 10572
(-3, 12): 20638
(-3, 13): 44928
(-3, 14): 76863
(-3, 15): 131788
(-3, 16): 144094
(-3, 17): 180728
(-3, 18): 159764
(-3, 19): 140514
(-3, 20): 80270
(-3, 21): 49299
(-3, 22): 16194
(-3, 23): 5656
(-3, 24): 740
(-3, 25): 32
(-2, 8): 90
(-2, 9): 1646
(-2, 10): 10496
(-2, 11): 37438
(-2, 12): 102936
(-2, 13): 209846
(-2, 14): 374660
(-2, 15): 544082
(-2, 16): 747820
(-2, 17): 816110
(-2, 18): 839808
(-2, 19): 678376
(-2, 20): 510184
(-2, 21): 287478
(-2, 22): 143424
(-2, 23): 50400
(-2, 24): 14306
(-2, 25): 2528
(-2, 26): 244
(-2, 27): 10
(-1, 5): 3
(-1, 6): 60
(-1, 7): 600
(-1, 8): 3540
(-1, 9): 14370
(-1, 10): 42577
(-1, 11): 109472
(-1, 12): 230064
(-1, 13): 443818
(-1, 14): 716938
(-1, 15): 1089688
(-1, 16): 1418000
(-1, 17): 1731826
(-1, 18): 1775873
(-1, 19): 1720842
(-1, 20): 1388336
(-1, 21): 1020259
(-1, 22): 617177
(-1, 23): 321024
(-1, 24): 132574
(-1, 25): 43636
(-1, 26): 10808
(-1, 27): 1940
(-1, 28): 246
(-1, 29): 21
(-1, 30): 1
(1, 5): 3
(1, 6): 60
(1, 7): 600
(1, 8): 3540
(1, 9): 14370
(1, 10): 42293
(1, 11): 109048
(1, 12): 229296
(1, 13): 442982
(1, 14): 716702
(1, 15): 1090112
(1, 16): 1418680
(1, 17): 1733834
(1, 18): 1778197
(1, 19): 1723158
(1, 20): 1389964
(1, 21): 1020811
(1, 22): 616123
(1, 23): 318936
(1, 24): 130406
(1, 25): 42116
(1, 26): 10042
(1, 27): 1660
(1, 28): 174
(1, 29): 9
(2, 8): 90
(2, 9): 1474
(2, 10): 10216
(2, 11): 36782
(2, 12): 102384
(2, 13): 209554
(2, 14): 374500
(2, 15): 544558
(2, 16): 748940
(2, 17): 817330
(2, 18): 841432
(2, 19): 679544
(2, 20): 510800
(2, 21): 287202
(2, 22): 142896
(2, 23): 49920
(2, 24): 14074
(2, 25): 2464
(2, 26): 236
(2, 27): 10
(3, 8): 118
(3, 9): 944
(3, 10): 3978
(3, 11): 10428
(3, 12): 20462
(3, 13): 44772
(3, 14): 76947
(3, 15): 131828
(3, 16): 144686
(3, 17): 181372
(3, 18): 160216
(3, 19): 140886
(3, 20): 80122
(3, 21): 49011
(3, 22): 15861
(3, 23): 5504
(3, 24): 700
(3, 25): 28
(4, 7): 9
(4, 8): 56
(4, 9): 172
(4, 10): 126
(4, 11): 1630
(4, 12): 10989
(4, 13): 25164
(4, 14): 54042
(4, 15): 77554
(4, 16): 105543
(4, 17): 104848
(4, 18): 90738
(4, 19): 60036
(4, 20): 34515
(4, 21): 11404
(4, 22): 4094
(4, 23): 371
(4, 24): 5
(5, 10): 147
(5, 11): 1152
(5, 12): 1314
(5, 13): 5386
(5, 14): 7604
(5, 15): 10152
(5, 16): 16976
(5, 17): 16540
(5, 18): 13675
(5, 19): 8622
(5, 20): 4626
(5, 21): 1791
(5, 22): 267
(6, 10): 176
(6, 11): 416
(6, 12): 1196
(6, 13): 3016
(6, 14): 5908
(6, 15): 11738
(6, 16): 12032
(6, 17): 12620
(6, 18): 9636
(6, 19): 5588
(6, 20): 1676
(6, 21): 540
(7, 9): 10
(7, 12): 522
(7, 13): 285
(7, 14): 731
(7, 15): 1608
(7, 16): 1518
(7, 17): 1890
(7, 18): 1566
(7, 19): 414
(7, 20): 360
(8, 11): 28
(8, 12): 5
(8, 13): 354
(8, 14): 1076
(8, 15): 1132
(8, 16): 2141
(8, 17): 1254
(8, 18): 450
(8, 19): 450
(8, 20): 45
(9, 13): 90
(9, 14): 87
(9, 15): 180
(9, 17): 180
(9, 18): 194
Comment by Luke Pebody — March 3, 2017 @ 6:42 am |
Thanks for doing this! I decided to try to reproduce your calculation and got the same numbers (at least up to the sign of the determinant, which is controlled by one’s definition of “lexicographic order”). The first thing I notice is that the counts for (a,b) and (-a,b) and (a,36-b) and (-a,36-b) all tend to be close, but usually not exactly equal, to each other. It might be good to understand why this is the case, although unfortunately it would not help much with my cancellation idea because all these terms have the same sign.
Another observation is that for a fixed determinant, if we arrange the counts by the number of zeros, we do not get a unimodal sequence in general. That is not encouraging for the idea of seeking cancellation between adjacent terms of the sequence. Still, the sequence seems to be “almost” unimodal except at the edges, so maybe this idea is not out of the question.
Comment by tchow8 — March 5, 2017 @ 10:26 pm |
This formula identifies the difference as the top Fourier-Walsh coefficient of the function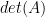 (defined on
(defined on 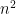 Boolean variables.)
Boolean variables.)
UPDATE: I overlooked the exponent. Corrected version: This formula identifies the difference as the top Fourier-Walsh coefficient of the function .
.
Comment by Gil Kalai — February 27, 2017 @ 9:06 am |
Let denote the number of even Latin squares with the first row and column in order, and
denote the number of even Latin squares with the first row and column in order, and 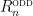 denote the number of odd Latin squares with the first row and column in order. The values of
denote the number of odd Latin squares with the first row and column in order. The values of ![s[n] := R_n^{\text{\sc even}} - R_n^{\text{\sc odd}}](https://s0.wp.com/latex.php?latex=s%5Bn%5D+%3A%3D+R_n%5E%7B%5Ctext%7B%5Csc+even%7D%7D+-+R_n%5E%7B%5Ctext%7B%5Csc+odd%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) are
are  when
when  . [Stones and Wanless (2012)]
. [Stones and Wanless (2012)]
I just stumbled upon the surprising property: for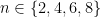 , this sequence has the property that
, this sequence has the property that ![s[n+1] = (n-1)! s[n].](https://s0.wp.com/latex.php?latex=s%5Bn%2B1%5D+%3D+%28n-1%29%21+s%5Bn%5D.&bg=ffffff&fg=000000&s=0&c=20201002) What’s up with that?! I find it hard to believe this is just a small-case numerical coincidence, since when
What’s up with that?! I find it hard to believe this is just a small-case numerical coincidence, since when  we have
we have ![s[9] = 31302667468800 = 6210846720 \cdot 7! = s[8] \cdot 7!](https://s0.wp.com/latex.php?latex=s%5B9%5D+%3D+31302667468800+%3D+6210846720+%5Ccdot+7%21+%3D+s%5B8%5D+%5Ccdot+7%21&bg=ffffff&fg=000000&s=0&c=20201002) which are some big numbers.
which are some big numbers.
In Stones and Wanless (2012), we conjectured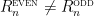 for all n. If the above observation is true for all even n, then the Alon-Tarsi Conjecture also implies our conjecture. I.e., the two conjectures are equivalent.
for all n. If the above observation is true for all even n, then the Alon-Tarsi Conjecture also implies our conjecture. I.e., the two conjectures are equivalent.
Comment by rebeccastones82 — March 11, 2017 @ 12:10 pm |
This is fascinating! In these small terms also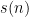 divides
divides 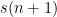 for every
for every  . But I suppose we know from Glynn’s result that 13 that divides
. But I suppose we know from Glynn’s result that 13 that divides  does not divide
does not divide  .
.
Comment by Gil Kalai — March 11, 2017 @ 5:01 pm |
Daniel Kotlar pointed out that this observation is true for even n>=2 is Theorem 3.3 in Aharoni and Loebl, “The odd case of Rota’s bases conjecture” (2015). http://dx.doi.org/10.1016/j.aim.2015.06.015
Comment by rebeccastones82 — March 12, 2017 @ 8:03 am |
I think I managed to derive two formulas (I’m not sure if they will be of use):
For , we have
, we have ![L_n^{\text{\sc even}} - L_n^{\text{\sc odd}} = n! \sum_{A \in B_{n-1,n}} (-1)^{\sigma_0(A)} \prod_{j \in [n]} \det(A^{\langle j \rangle})](https://s0.wp.com/latex.php?latex=L_n%5E%7B%5Ctext%7B%5Csc+even%7D%7D+-+L_n%5E%7B%5Ctext%7B%5Csc+odd%7D%7D+%3D+n%21+%5Csum_%7BA+%5Cin+B_%7Bn-1%2Cn%7D%7D+%28-1%29%5E%7B%5Csigma_0%28A%29%7D+%5Cprod_%7Bj+%5Cin+%5Bn%5D%7D+%5Cdet%28A%5E%7B%5Clangle+j+%5Crangle%7D%29&bg=ffffff&fg=000000&s=0&c=20201002) where
where  is the set of
is the set of 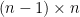
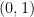 -matrices,
-matrices,  is the number of
is the number of 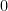 ‘s in
‘s in  , and
, and 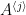 is the matrix formed by deleting the
is the matrix formed by deleting the 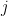 -th column of
-th column of  .
.
For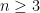 , we have
, we have  where
where 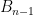 is the set of
is the set of 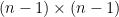
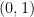 -matrices,
-matrices,  is the number of
is the number of 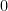 ‘s in
‘s in  , and
, and  is the matrix of minors satisfying
is the matrix of minors satisfying 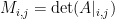 for all
for all ![i,j \in [n-1]](https://s0.wp.com/latex.php?latex=i%2Cj+%5Cin+%5Bn-1%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Since the proofs are cumbersome and my WordPress LaTeX skills are not great, I wrote up what I’ve done at Overleaf: https://www.overleaf.com/8425738kswcbnfsfzqw
Comment by rebeccastones82 — March 12, 2017 @ 12:16 pm |
The question after Idea 1 seems to easy. Just pick two elements in distinct rows that are independent and start the two triangles with them as the respective ‘s. Then merge the two
‘s. Then merge the two 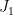 ‘s at the end. Of course one could improve on this to get better bounds on
‘s at the end. Of course one could improve on this to get better bounds on  .
.
Comment by domotorp — February 24, 2017 @ 2:37 pm |
OK, this was complete nonsense, I’ve completely misunderstood something and swapped and
and 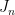 . If any of the two people who have upvoted my comment really see some solution, please let me know…
. If any of the two people who have upvoted my comment really see some solution, please let me know…
Comment by domotorp — February 24, 2017 @ 7:58 pm |
I was one of the upvoters but I now see that I made the same mistake that you did.
Comment by tchow8 — February 24, 2017 @ 8:59 pm |
Here is an idea.
One corollary of our topological method is the following:
If we find k disjoint base transversals, then we can cover the rest with 2n-2k independent transversals.
So altogether we cover everything with 2n-k independent transversals.
I am not sure, but I think it is known that 2 disjoint base transversals can always be found.
Comment by Eli Berger — February 26, 2017 @ 12:51 am |
It was proved by Geelen and Webb that one can find \sqrt(n) base transversals.
Comment by ShiraZ — February 26, 2017 @ 8:53 pm |
Sorry, but I don’t think this is true for k=n-1. It says if you have n-1 disjoint base traversals then the remaining elements can be covered by 2 independent transversal.
Counterexample: B1=B2={e1, e2, e3} and B3={e1, e1+e2, e1+e3} and the two disjoint base traversals are (e2, e3, e1+e2) and (e3, e2, e1+e3). The remaining elements are all e1 and so need 3 independent transversals to cover them.
Comment by Luke Pebody — February 27, 2017 @ 9:47 pm |
Yes, it looks like you are right. The topological method does not give what I thought it would.
Comment by Eli Berger — March 8, 2017 @ 7:28 pm |
So here is a (hopefully) correct solution that shows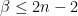 . We start as proposed, with two triangles. We do the procedure to get all the
. We start as proposed, with two triangles. We do the procedure to get all the  in one of them. Denote the only element of
in one of them. Denote the only element of 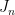 by
by 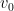 . I claim that given any triangle
. I claim that given any triangle 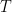 with
with  rows, of size
rows, of size 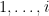 independent sets, we can select
independent sets, we can select  transversal independent sets from
transversal independent sets from 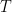 such that
such that 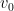 can be added to the size
can be added to the size 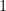 independent set, IF the only element of the row of
independent set, IF the only element of the row of 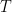 that has size
that has size 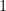 forms an independent set with
forms an independent set with 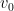 . The statement of this claim is quite long (and probably shouldn’t be squeezed into one sentence), but its proof is trivial by induction. So how can we guarantee that the second triangle satisfies the IF condition with
. The statement of this claim is quite long (and probably shouldn’t be squeezed into one sentence), but its proof is trivial by induction. So how can we guarantee that the second triangle satisfies the IF condition with 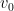 ? By carefully picking when creating
? By carefully picking when creating 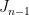 in the first triangle (and using that
in the first triangle (and using that 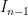 is an independent set).
is an independent set).
Comment by domotorp — February 24, 2017 @ 10:11 pm |
Just to clarify, above size $\atex 1$ independent set means the size $\atex 1$ transversal (and in fact transversals shouldn’t be called transversals, as they doesn’t intersect all the rows, I’m not sure what word would be appropriate).
Comment by domotorp — February 24, 2017 @ 10:29 pm |
I think this works, but the trivial part didn’t seem trivial to me so I want to spell it out here. Suppose the claim is true for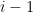 , and let
, and let  be the rows of
be the rows of 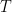 . The plan is to construct the first transversal
. The plan is to construct the first transversal 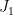 , delete it, and apply the induction hypothesis to the resulting smaller triangular system. For this to work, we have to make sure that the unique remaining element
, delete it, and apply the induction hypothesis to the resulting smaller triangular system. For this to work, we have to make sure that the unique remaining element  forms an independent set with
forms an independent set with 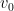 . The only way things could go wrong is if
. The only way things could go wrong is if 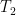 contains an element
contains an element  parallel to
parallel to 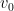 and we fail to put
and we fail to put  in
in 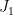 . However, when we are constructing
. However, when we are constructing 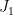 , we are free to pick any element from
, we are free to pick any element from 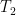 as long as it forms an independent set with the unique element
as long as it forms an independent set with the unique element  . But since
. But since 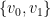 is independent by hypothesis and
is independent by hypothesis and 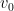 is parallel to
is parallel to  , it follows that
, it follows that 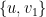 is independent, so we can indeed arrange for
is independent, so we can indeed arrange for  to be in
to be in 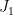 (the other element of
(the other element of 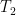 cannot also be parallel to
cannot also be parallel to 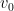 since
since 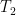 is independent).
is independent).
Comment by tchow8 — February 25, 2017 @ 2:28 am |
Yes, this is exactly what I had in mind.
Comment by domotorp — February 25, 2017 @ 6:47 am |
Tim, in your proposal on mathoverflow you say: “The problem feels to me like it falls into the category of problems that have too little structure for a purely deterministic construction but too much structure for a purely random construction. A number of difficult problems of this type have fallen in recent years so the time may be ripe for another such.” I would like to know what these problems are to get a better idea of what you mean by this category of problems. Maybe this will also suggest some general directions for Rota’s basis conjecture itself.
Comment by NG — February 24, 2017 @ 3:57 pm |
There’s a nice survey by Gowers in the most recent Bull. AMS on the construction of block designs on exactly this type of issue, the problems that fall between the probabilistic method and deterministic methods. He discusses the work of Keevash, which finds a large structured sub-solution, fills in much of the rest randomly, and then uses the structure of the first part to generate enough moves to fill in the holes left by the randomness. See http://www.ams.org/journals/bull/2017-54-01/S0273-0979-2016-01553-9/
Comment by David Eppstein — February 24, 2017 @ 4:50 pm |
In addition to the Gowers paper mentioned by David Eppstein, which mentions not just Keevash’s work but also the “middle layers problem” (is the graph induced by the middle two layers of an odd-dimensional Boolean algebra Hamiltonian?), I recommend reading Danny Calegari’s comment on Gil Kalai’s blog on the same topic.
There are a couple of reasons why I think that Rota’s basis conjecture might fall into this “intermediate” category. First, if you start playing around a little, then you get the feeling that for any given set of bases, there is not just one solution but a vast number of solutions. For example, if all the bases are equal, then we are just looking for Latin squares, and there are lots of these. Furthermore, intuitively it seems that having all the bases equal is the “worst case” as far as the number of solutions goes, because equal bases give rise to a lot of linear dependencies. I would expect that other sets of bases admit even more solutions. Given that there are a lot of solutions, it is tempting to try a random construction. However, a naive random construction will produce undesired linear dependencies with high probability. On the other hand, if one tries an explicit deterministic construction, one quickly branches into a lot of different cases, and it seems very difficult to control all the different cases that arise. Of course, perhaps the right insight will show how to control the different cases, but so far nobody seems to have had that insight.
A second reason comes from the connection with the Alon-Tarsi conjecture. If you are not familiar with this connection, then I recommend Shmuel Onn’s Monthly article for an accessible exposition. Briefly, there is a polynomial identity with the general form “sum = coefficient*product” where the hypothesis of Rota’s basis conjecture implies that the product is nonzero and the desired conclusion of the conjecture is that one of the summands is nonzero. The Alon-Tarsi conjecture is that the coefficient is nonzero, and therefore it implies Rota’s basis conjecture. They key point is that the sum is huge (it is essentially a sum over all possible grids) and so this proof is “non-constructive” in the sense that it does not yield a polynomial time algorithm for finding which summand is nonzero, which is what we need in order to construct the desired grid. To me, this is a hint that it may not suffice to think purely in terms of an explicit polytime construction of the desired grid.
By the way, the aforementioned polynomial identity is related to the Nullstellensatz, though it does not seem to arise in the way that the combinatorial Nullstellensatz typically arises in “non-constructive combinatorics” (but I would love it if someone proved me wrong on this point by connecting Rota’s basis conjecture with other combinatorial Nullstellensatz problems).
Comment by tchow8 — February 24, 2017 @ 6:32 pm |
A result of Edmonds [Theorem 1 of “Minimum partition of a matroid into independent subsets,”
Journal of Research of the National Bureau of Standards 69B (1965), 67–72] is the following:
Theorem 1. Let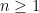 . A finite matroid
. A finite matroid  with rank function
with rank function  can be partitioned into
can be partitioned into  pairwise disjoint independent sets if and only if, for all subsets
pairwise disjoint independent sets if and only if, for all subsets  of
of  ,
,
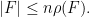
This implies (Mirsky, Transversal Theory, Corollary 3.3.4):
Theorem 2. Let . Let
. Let 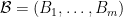 be a family of subsets of a finite set
be a family of subsets of a finite set  . For
. For  , let
, let  be the size of the largest partial transversal of
be the size of the largest partial transversal of  contained in
contained in  .
.
Then can be partitioned into
can be partitioned into  pairwise disjoint partial transversals if and only if, for all subsets
pairwise disjoint partial transversals if and only if, for all subsets  of
of  ,
,
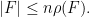
The natural “join” of Theorems 1 and 2 to partial independent transversals is known to be false (pp. 93–94 of de Sousa, “Disjoint common transversals,” in: D. J. A. Welsh (ed.), Combinatorial Mathematics and Its Applications: Proceedings of a Conference Held at the Mathematical Institute, Oxford, from 7–10 July, 1969, Academic Press,
London and New York, 1971, pp. 87–94). But we do have the following:
Proposition 3. Let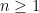 . Let
. Let  be an
be an  -dimensional vector space. Let
-dimensional vector space. Let 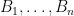 be bases for
be bases for  that are pairwise disjoint. Let
that are pairwise disjoint. Let 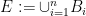 .
.
Then for all ,
,
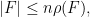
 is the size of the largest linearly independent partial transversal of
is the size of the largest linearly independent partial transversal of 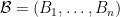 that is a subset of
that is a subset of  .
.
where
This is in the groundbreaking, paradigm-shifting paper by Farley,* “A Problem Attributed to Rado from Mirsky’s 1971 Monograph Transversal Theory and a Conjecture from the 1982 Proceedings of the American Mathematical Society,” Math. Pannon. 24 (2013), no. 1, 3–14.
I am not suggesting that this is a sufficient condition, but it is worth exploring how far we can push this.
*This is an attempt at humor. I am a professional humorist: do not attempt this on your own!
Comment by Jonathan Farley — February 24, 2017 @ 4:10 pm |
What do you mean by “exploring how far we can push this”? Do you have a specific conjecture in mind that might be tractable and that might bring us closer to Rota’s basis conjecture?
Comment by tchow8 — February 25, 2017 @ 3:22 am |
[…] This is a quick post to draw attention to the fact that a new and very interesting looking polymath project has just started, led by Timothy Chow. He is running it over at the Polymath blog. […]
Pingback by Timothy Chow starts Polymath12 | Gowers's Weblog — February 24, 2017 @ 4:40 pm |
Thanks for mentioning our paper!
A quick thought: if you were going to degenerate, what you would need to do is say: is there any version of this question that makes sense when the basic object is, instead of a basis of an n-dimensional vector space V, a 0-dimensional subscheme of V of degree n which is not contained in any hyperplane? For instance, in 2-space you could have something which was totally supported at the point (0,1) but which was “fat” in the horizontal direction of degree 2. (This is the scheme S such that what it means for a curve C to contain S is that S passes through (0,1) and has a horizontal tangent there.) This comment is probably not helpful for people who don’t already think about schemes but I wanted to put something down as a placeholder.
Comment by JSE — February 24, 2017 @ 6:39 pm |
I don’t know if this helps, but let me offer another restatement of the “degenerate” case that I described above. Let be sets of integers, where each
be sets of integers, where each 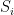 consists of
consists of  distinct integers (but
distinct integers (but 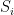 and
and  may have nonempty intersection). Then there exists an
may have nonempty intersection). Then there exists an 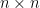 grid whose
grid whose  th row comprises the elements of
th row comprises the elements of 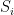 (in some order) and whose columns all consist of distinct integers. This is a theorem.
(in some order) and whose columns all consist of distinct integers. This is a theorem.
In fact something stronger is true (Dinitz’s conjecture/Galvin’s theorem). Given any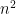 sets
sets 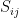 , each consisting of
, each consisting of  distinct integers, there exists a way of choosing some
distinct integers, there exists a way of choosing some 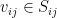 such that
such that  (for all
(for all  and
and 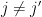 ) and
) and 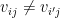 (for all
(for all 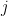 and
and 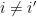 ). The previous paragraph is the special case where
). The previous paragraph is the special case where  for all
for all 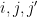 .
.
Comment by tchow8 — February 24, 2017 @ 6:58 pm |
Aha, great, I was trying to figure out what the statement was that was “finite sets in both directions.” What’s funny about the question at hand is that it’s “horizontally” about S_n and finite sets, and “vertically” about GL_n and finite-dimensional vector spaces.
What’s the statement that’s about vector spaces both horizontally and vertically?
Comment by JSE — February 25, 2017 @ 5:31 am |
I suppose it would say: you have a collection V_1, … V_n of n-dimensional subspaces of k^N. Then the question is whether you can write down an n x n grid whose row i is a basis for V_i, and whose columns are independent sets of vectors. Is that always possible? (In the spirit of polymath I am asking this question without thinking about it.)
Comment by JSE — February 25, 2017 @ 5:33 am |
Nice question. I think that the following argument shows that the answer is yes. The key fact is that a vector space is never the union of of two proper subspaces (where a “subspace” must contain the origin; affine subspaces don’t count). I’m not sure I can cite a reference for this folklore fact but maybe someone else can. Anyway, given this, the idea is to construct the desired grid one column at a time, filling in each column one vector at a time from (say) the top to the bottom. If you’re at location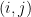 then you just have to find some vector in
then you just have to find some vector in 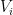 that is not in the subspace
that is not in the subspace 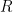 spanned by the preceding
spanned by the preceding 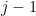 vectors in row
vectors in row  and also not in the subspace
and also not in the subspace 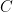 spanned by the preceding
spanned by the preceding 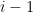 vectors in column
vectors in column 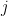 . But the aforementioned “key fact” implies that there is always some vector in
. But the aforementioned “key fact” implies that there is always some vector in 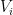 that is not in
that is not in 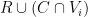 .
.
Comment by tchow8 — February 26, 2017 @ 8:43 pm |
[…] 12 is hosted by Timothy Chow and you can click here to follow the progress or to […]
Pingback by Polymath 12: Rota’s Basis Conjecture | The Matroid Union — February 25, 2017 @ 3:14 pm |
Dear all, when I tried to write from memory the Rota basis conjecture (in my blog for advertising polymath12) I wrote the following more general version: if you have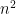 bases
bases 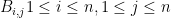 of an
of an  -dimensional vector space then you can choose
-dimensional vector space then you can choose 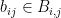 such that for every
such that for every 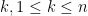 , the vectors
, the vectors  form a basis of
form a basis of  and also the vectors
and also the vectors  form a basis. This conjecture can be regarded as a strengthening of the Dinits Conjecture whose solution by Galvin is described in this post. Is this more general version known to be equivalent to the one stated here or perhaps known to be false?
form a basis. This conjecture can be regarded as a strengthening of the Dinits Conjecture whose solution by Galvin is described in this post. Is this more general version known to be equivalent to the one stated here or perhaps known to be false?
Comment by Gil Kalai — February 25, 2017 @ 4:21 pm |
Gil – for proper acknowledgement of authorship: I know this (really nice) version of the conjecture as “(Jeff) Kahn’s conjecture” – though a quick search on the internet didn’t yield a reference. And no, the conjectures do not seem equivalent (though probably they are, in the sense of both being true).
Comment by Ron Aharoni — February 25, 2017 @ 6:18 pm |
Dear Ron, thanks! probably I heard it from Jeff. Does the Alon-Tarsi conjecture imply this stronger version as well? Also, does the Alon-Tarsi “polynomial” criterion for choosability also implies analogous “independent sets ” coloring?
Comment by Gil Kalai — February 25, 2017 @ 6:55 pm |
I doubt that the Alon-Tarsi conjecture impiles the stronger version, but we might be able to derive an analogous result for the “Kahn conjecture” as follows. The Kahn conjecture involves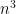 vectors; let
vectors; let  denote the
denote the  th candidate vector at position
th candidate vector at position 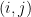 . Think of each
. Think of each  as a vector of indeterminates
as a vector of indeterminates 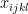 . For each
. For each 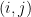 , we can form an
, we can form an 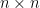 matrix consisting of the indeterminates
matrix consisting of the indeterminates 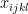 with the given
with the given 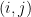 value; let
value; let 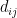 denote the determinant of this matrix, and let
denote the determinant of this matrix, and let 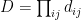 . Now, for any way
. Now, for any way  of selecting one vector per location
of selecting one vector per location 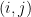 , we can look at any row or column and form a matrix out of the selected vectors in that row or column and consider its determinant; let
, we can look at any row or column and form a matrix out of the selected vectors in that row or column and consider its determinant; let  denote the product of these
denote the product of these 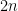 determinants. We can now seek to express
determinants. We can now seek to express 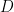 explicitly as some weighted combination of all the
explicitly as some weighted combination of all the  . By the Nullstellensatz, if the Kahn conjecture is true, then it must be possible to express *some power* of
. By the Nullstellensatz, if the Kahn conjecture is true, then it must be possible to express *some power* of 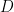 as some *polynomial* linear combination of the
as some *polynomial* linear combination of the  . The nice thing about Rota’s conjecture is that we don’t have raise (the analogue of)
. The nice thing about Rota’s conjecture is that we don’t have raise (the analogue of) 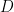 to any power;
to any power; 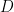 itself suffices, and we can take a *scalar* linear combination because the degrees are the same on both sides. Things aren’t going to be as simple for the Kahn conjecture because for starters the degree of
itself suffices, and we can take a *scalar* linear combination because the degrees are the same on both sides. Things aren’t going to be as simple for the Kahn conjecture because for starters the degree of 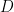 is
is 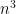 while the degree of
while the degree of  is
is 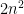 , but maybe something can still be done. I’m not aware of anyone who has tried this.
, but maybe something can still be done. I’m not aware of anyone who has tried this.
I don’t understand your second question so I can’t comment on it.
Comment by tchow8 — February 26, 2017 @ 9:09 pm |
It is Conjecture 6 of Huang and Rota, “On the relations of various conjectures on Latin squares and straightening coefficients,” Discrete Math. 128 (1994), no. 1-3, 225–236, although for some reason Professor Rota keeps saying the field is infinite. They attribute it to Jeff Kahn in 1991.
Comment by Jonathan Farley — February 26, 2017 @ 2:36 am |
The “graphic matroid” version of this question would be, I think: you have a set of n-1 trees T_1, .. T_{n-1} on n vertices. Can you order the edges of each tree in such a way that, for every i, the graph formed by e_i(T_1), .. e_i(T_{n-1}) is a tree?
Is this a known question? Do we think it’s true or not? Does the Aharoni-Berger theorem say something interesting in this case?
Comment by JSE — February 25, 2017 @ 11:26 pm |
This may be completely wrong, but doesn’t this tree question follow from the main question? If we associate with each edge the linear combination
the linear combination 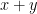 with coefficients in
with coefficients in 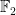 , then a set of edges is linearly independent if and only if it does not contain a cycle. Since all edges have coefficients that sum to zero, they live in an
, then a set of edges is linearly independent if and only if it does not contain a cycle. Since all edges have coefficients that sum to zero, they live in an 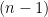 -dimensional space, so trees are precisely bases in this space.
-dimensional space, so trees are precisely bases in this space.
Comment by gowers — February 26, 2017 @ 12:19 am |
Yes. Matroid theorists would say, “Graphic matroids are regular, meaning that they are representable over any field.”
Comment by tchow8 — February 26, 2017 @ 9:47 pm |
Of course, if what I’ve written is correct, that doesn’t necessarily mean your question is uninteresting — it could be a very good case to consider of the main question.
Comment by gowers — February 26, 2017 @ 12:20 am |
A tiny extra remark is that I didn’t need the scalars to be in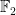 : indeed, the standard thing to do is associate with the edge
: indeed, the standard thing to do is associate with the edge  the vector
the vector 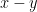 (which is what we did in
(which is what we did in 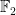 , but it works in any field). It remains the case that these vectors form a basis of the space of functions that add up to zero if and only if the graph is a tree.
, but it works in any field). It remains the case that these vectors form a basis of the space of functions that add up to zero if and only if the graph is a tree.
Comment by gowers — February 26, 2017 @ 5:46 pm |
I was actually wondering, regarding Tim G’s “extra remark”: do we expect the Rota conjecture to be true in characteristic 2? The paper of Stones and Wanless referred to above seems to say that the Alon-Tarsi constants are always even. But of course Rota might still hold.
Comment by JSE — February 26, 2017 @ 6:30 pm |
Let me refine this a little bit. Another way to go is to consider a fixed graph G whose graphic matroid has rank n. (I am not a matroidologist so forgive me if I mess up the terminology.) For instance, G could be n disjoint edges on 2n vertices, or G could be K_{n+1}, or any other connected graph on n+1 vertices.
Then we can ask: given B_1, … B_n a set of maximal independent sets (i.e. spanning forests of G), can you order the elements (i.e. edges) of each B_j such that, for every i, the set e_i(B_1), .. e_i(B_n) is a spanning forest? How many such ways are there?
This might be a good way to “interpolate” between easy questions and harder ones. When G is n disjoint edges, then B_1, .. B_n are all the same thing and this is just a Latin squares problem, well-understood. When G is the complete graph on n+1 vertices, it’s the question I posted above. How dense does G have to get before the problem starts getting difficult? (Or does it ever get difficult?) Of course, as Tim Gowers says, these are all special cases of the Rota conjecture, but maybe they’re interesting special cases.
Comment by JSE — February 26, 2017 @ 6:48 pm |
I guess taking G a tree on n+1 vertices is the same as n disjoint edges on 2n distinct vertices, not sure why I made the distinction.
Comment by JSE — February 26, 2017 @ 9:39 pm |
I expect Rota’s basis conjecture to be true for arbitrary matroids. No counterexample is known. Rota himself was only confident of its truth for vector spaces of even dimension, essentially because of the Alon-Tarsi connection, and the work of Bollen and Draisma on the online version of the conjecture gives further indication that the odd-dimensional case is different, but at the moment I think it make sense to conjecture it for arbitrary matroids.
Graphic matroids or binary matroids would be interesting special cases. They are not known to be true. As far as I know, the only two interesting classes of matroids for which the conjecture is known are strongly base-orderable matroids (due to Wild) and paving matroids (due to Geelen and Humphries). Paving matroids are matroids whose circuits all have size or
or 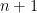 . I think it would be very interesting to attempt to extend this result to matroids whose circuits all have size at least
. I think it would be very interesting to attempt to extend this result to matroids whose circuits all have size at least  . Strong base-orderability is a rather technical condition and it is a very special class of matroids; my personal perspective is that these are matroids with “no local obstructions” and my “Idea 2” can be thought of as doing a computational search for local obstructions.
. Strong base-orderability is a rather technical condition and it is a very special class of matroids; my personal perspective is that these are matroids with “no local obstructions” and my “Idea 2” can be thought of as doing a computational search for local obstructions.
Comment by tchow8 — February 26, 2017 @ 9:21 pm |
Suppose that $M_1$ and $M_2$ are matroids that both obey the basis conjecture. Is it known that their disjoint union also obeys the basis conjecture? (It’s very easy to find a binary matrix that describes which of $M_1$ and $M_2$ to choose from so that you get the right number of elements from each matroid in each row and column. Just choose rank($M_1$) diagonals to be 0’s and the rest 1’s. The harder part is choosing which elements of each matroid to use to replace the 0’s and 1’s.) This seems vagely related to the triangular system lemma in idea 1.
Comment by David Eppstein — February 27, 2017 @ 1:50 am |
Another nice question! I don’t know the answer, but it suggests that perhaps we should consider the following strengthening of the conjecture, which I’ll phrase in terms of vector spaces in case some readers are not comfortable with matroids. Suppose we are given bases
bases 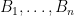 of a vector space of dimension
of a vector space of dimension 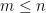 , and suppose we are given an
, and suppose we are given an 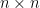 0-1 matrix with exactly
0-1 matrix with exactly  1’s in every row and column. Can we replace each 1 in the matrix with a vector in such a way that the
1’s in every row and column. Can we replace each 1 in the matrix with a vector in such a way that the  vectors in row
vectors in row  are the elements of
are the elements of 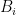 and such that the
and such that the  vectors in every column is a basis? Then I think the property of satisfying this conjecture is closed under disjoint union (a Hall’s marriage theorem argument shows that any 0-1 matrix of the stated form is the sum of
vectors in every column is a basis? Then I think the property of satisfying this conjecture is closed under disjoint union (a Hall’s marriage theorem argument shows that any 0-1 matrix of the stated form is the sum of  permutation matrices).
permutation matrices).
Comment by tchow8 — February 27, 2017 @ 2:07 am |
[…] Timothy Chow of MIT has proposed a new Polymath project: resolve Rota’s basis conjecture. […]
Pingback by The 12th Polymath project has started: resolve Rota’s basis conjecture | The Aperiodical — February 26, 2017 @ 11:52 am |
Related to Idea 3, suppose that we are given collections of
collections of  vectors,
vectors,  , in an
, in an  -dimensional space. What are necessary and sufficient conditions that allow us to pick $k$ transversal bases? I expect this to be NP-hard already for constant
-dimensional space. What are necessary and sufficient conditions that allow us to pick $k$ transversal bases? I expect this to be NP-hard already for constant  , but some strong enough sufficient condition would be, well, sufficient. For example, it seems to me that in Rota’s original conjecture, no matter how we pick a first transversal basis, we can always extend it into a system of
, but some strong enough sufficient condition would be, well, sufficient. For example, it seems to me that in Rota’s original conjecture, no matter how we pick a first transversal basis, we can always extend it into a system of  transversal bases. But what is the condition that we have to maintain when we pick the second basis?
transversal bases. But what is the condition that we have to maintain when we pick the second basis?
Comment by domotorp — February 26, 2017 @ 12:09 pm |
I think you mean “Idea 2” rather than “Idea 3.” It is not true that you can pick the first transversal basis however you want. This is probably a good moment to introduce one of the basic counterexamples in the subject, namely , the complete graph on four vertices. This graph has six edges, which I wll call 12, 13, 14, 23, 24, and 34, in honor of their endvertices. As Tim Gowers explained above, you can associate a vector to each of these edges in such a way that a subset of the vectors is linearly independent if and only if the corresponding edges do not contain a cycle. So now consider the following 3 sets of 2 edges/vectors: {12,34}, {13,24}, {23,14}. It is easy to check that there is no way to pick 2 disjoint transversal bases. So if you have a 3×3 instance of Rota’s basis conjecture and you pick your first basis in such a way as to leave a copy of
, the complete graph on four vertices. This graph has six edges, which I wll call 12, 13, 14, 23, 24, and 34, in honor of their endvertices. As Tim Gowers explained above, you can associate a vector to each of these edges in such a way that a subset of the vectors is linearly independent if and only if the corresponding edges do not contain a cycle. So now consider the following 3 sets of 2 edges/vectors: {12,34}, {13,24}, {23,14}. It is easy to check that there is no way to pick 2 disjoint transversal bases. So if you have a 3×3 instance of Rota’s basis conjecture and you pick your first basis in such a way as to leave a copy of  in this way, then you’re stuck.
in this way, then you’re stuck.
Comment by tchow8 — February 26, 2017 @ 9:42 pm |
[…] Chow launched polymath12 devoted to the Rota Basis conjecture on the polymathblog. A classic paper on the subject is the 1989 paper by Rosa Huang and Gian […]
Pingback by Timothy Chow Launched Polymath12 on Rota Basis Conjecture and Other News | Combinatorics and more — February 26, 2017 @ 2:54 pm |
I remember that a certain combinatorial result of the form “given several bases of , we may choose an element from each basis so that…” is proved in our paper with Roman Karasev (Israel Journal of Mathematics 2012) using some sophisticated algebraic topology. This part of a paper is entirely Roman’s, and I do not know how to do the same with polynomial tools.
, we may choose an element from each basis so that…” is proved in our paper with Roman Karasev (Israel Journal of Mathematics 2012) using some sophisticated algebraic topology. This part of a paper is entirely Roman’s, and I do not know how to do the same with polynomial tools.
We may try to modify the method.
Comment by Fedor Petrov — February 26, 2017 @ 9:48 pm |
This sounds very interesting. For the benefit of others let me restate your theorem here. Let be an odd prime, and let
be an odd prime, and let  be the
be the 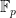 -vector space of dimension
-vector space of dimension  . Denote
. Denote 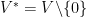 and put
and put 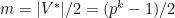 . Suppose we are given
. Suppose we are given  linear bases of the vector space
linear bases of the vector space 
Then there exist pairwise distinct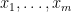 ,
, 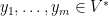 and a map
and a map ![g:[m] \to [k]](https://s0.wp.com/latex.php?latex=g%3A%5Bm%5D+%5Cto+%5Bk%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that for every
such that for every  we have
we have 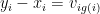 .
.
It is intriguing to me that topological methods are used in the proof since topology is also used by Aharoni-Berger.
Comment by tchow8 — February 27, 2017 @ 3:53 pm |
In “Ten Mathematics Problems I Will Never Solve,” Professor Rota refers to proofs by Marini for n=2,3,4,6,8. Can someone please post links to these proofs?
Comment by Anonymous — February 27, 2017 @ 7:28 am |
I didn’t leave my details. (I am new to this.)
Comment by Jonathan Farley — February 27, 2017 @ 7:31 am |
I am pretty sure that Marini never published anything, and also that for n=4,6,8, it was just a computational verification of what we now call the Alon-Tarsi conjecture (and so, strictly speaking, was not a proof that worked over an arbitrary field). For n=2,3 it is not hard to put together a case-by-case proof.
Comment by tchow8 — February 27, 2017 @ 3:43 pm |
Regarding the case k=2 and n=5 in Idea 2, I have done a computer search for matroid counterexamples and I believe every case either has one of the two following forms (subject to rearrangement of individual pairs and the ordering of the pairs):
Case 1: Two pairs are (a1, a2), (b1, b2), there is some element from the other three pairs that forms a circuit with a1 and b1, and with a2 and b2 and there is some other element from the other three pairs that forms a circuit with a1 and b2 and with a2 and b1.
Example: (e1-e2,e3-e4), (e2-e3,e1-e4), (e1-e3,??), (e2-e4,??), (??,??)
Proof that there aren’t two disjoint independent transversals: If e1-e2 is paired with e2-e3 and e3-e4 with e1-e4 then neither independent transversal can contain e1-e3. If, on the other hand, e1-e2 is paired with e1-e4 and e2-e3 with e3-e4 then neither independent transversal can contain e2-e4.
Case 2: Three pairs are (a1, a2), (b1, x2), (x1, b2) (hopefully reason for bizarre labelling will be obvious), x1 and x2 form a circuit, there is some element from the other two pairs that forms a circuit with a1 and b1, and with a2 and b2 and there is some other element from the other two pairs that forms a circuit with a1 and b2 and with a2 and b1.
Example: (e1-e2,e3-e4), (e2-e3,x), (x,e1-e4), (e1-e3,??), (e2-e4,??)
Proof that there aren’t two disjoint independent transversals: Since e4 can’t be paired with e4, e1+e3 and e2+e3 must be in different transversals, so one is paired with e1 and one is paired with e2 and the argument follows as in Case 1.
—
So basically every counterexample I have found comes down to a K4.
It would seem a bit hasty to conjecture that every counterexample for k=2 is of the form (a1, x1), (x1, x2), (x2, x3), …, (x(n-1), xn), (xn, a2), (b1, y1), (y1, y2), …, (yn, b2), with some remaining elements c1 and c2 such that circuits are formed by a1,b1,c1, by a2,b2,c1, by a1,b2,c1 and by a2,b2,c1.
You mentioned that you found 2 examples for k=2 and Harvey, Kiraly and Lau found a family of counterexamples. Do they all fit this pattern?
Comment by Luke Pebody — February 28, 2017 @ 6:20 am |
The conjecture above was indeed hasty, as it is definitely not true: (a1, e1), (a2, e2), (e1+e2, e1-e2), (b1, e3), (b2, e4), (e3+e4, e3-e4), (c1, x), (c2, y).
Clearly as in the previous examples, a1 and a2 need to be in different transversals, as do b1 and b2, so the argument above shows you can’t have two disjoint independent transversals.
But, we could ask the question ‘Does every counterexample for k=2 contain 6 elements that form a K4 matroid?’
Comment by Luke Pebody — February 28, 2017 @ 6:27 am |
Back pedalling entirely on this for now, as a second computer search has found some cases the first computer search missed. I must have made some unnecessary assumptions the first time around.
Comment by Luke Pebody — February 28, 2017 @ 8:48 am |
The k=2, n=4 example that I found is a matroid called J in Oxley’s book on Matroid Theory. In Euclidean 4-space we may for example take I1 = {(-2,3,0,1), (0,0,1,1)}, I2 = {(0,2,0,1), (1,0,3,1)}, I3 = {(1,0,0,1), (0,1,2,1)}, I4 = {(0,1,0,1), (4,0,0,1)}. Note that J is not representable over the field with two elements.
The Harvey-Kiraly-Lau counterexamples for larger k are based on a class of graphs mentioned in my paper. A “wheel” is a cycle (the “rim”) together with another vertex (the “center”) that is adjacent to every vertex on the cycle; the edges coming off the center are called “spokes.” Now create multiple copies (parallel edges) of each spoke. This doesn’t immediately yield a counterexample for larger k (some additional work is needed, and I think it is best if I refer you to the Harvey-Kiraly-Lau paper at this point) but wheels with multiple spokes are the fundamental combinatorial object underlying the counterexamples.
Comment by tchow8 — February 28, 2017 @ 7:25 pm |
A note that for matroids, and (I think) over infinite fields, the generalization of the Basis Conjecture you mention in Item 3 is equivalent to the Basis Conjecture.
For matroids, just take your matroid and throw away all independent sets of size greater than n.
Over infinite fields (I think) no vector space of dimension >=2 is the union of finitely many strict subspaces. As such, while the dimension is greater than n, the subspaces generated by I_1, I_2, …, I_n will be strict subspaces, and so there is a vector v that is not in any of those subspaces. Then if you form a basis containing v, and then remove the v coordinate, each of the sets I_j will still be independent, and any subset of the points that is independent afterwards would have been independent before.
Comment by Luke Pebody — February 28, 2017 @ 6:47 am |
The starting point of Alon-Tarsi’s theorem is the coloring polynomial of a graph with vertex set
with vertex set  ,
,  and connections with coloring and choosability.
and connections with coloring and choosability. .where the lambdas are weights associated to the edges. More broadly, perhaps we can replace the polynomials we use by a larger class of polynomials?
.where the lambdas are weights associated to the edges. More broadly, perhaps we can replace the polynomials we use by a larger class of polynomials?
Is there something similar that we can say if we consider the polynomial
Comment by Gil Kalai — February 28, 2017 @ 10:14 am |
Here is an angle from which I like to view Rota’s conjecture: the uncannily nice behavior of the intersection of two matroids.
This has at least three aspects. To discuss them I need some notation: , where
, where  is any hypergraph, is the minimal number of edges needed to cover
is any hypergraph, is the minimal number of edges needed to cover  (sometimes the notation
(sometimes the notation 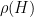 is used for that, but this is a bit confusing when matroids are discussed, where
is used for that, but this is a bit confusing when matroids are discussed, where 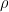 usually denotes rank).
usually denotes rank).
I. covering number. There is a conjecture of Eli Berger and myself, that if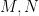 are two matroids on the same ground set, then
are two matroids on the same ground set, then  . That is, the intersection behaves almost as nicely as the worse of the two matroids. Konig’s edge coloring theorem yields the case of partition matroids, even without the
. That is, the intersection behaves almost as nicely as the worse of the two matroids. Konig’s edge coloring theorem yields the case of partition matroids, even without the 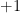 . The conjecture has been around for a while, and as yet there is no counterexample.
. The conjecture has been around for a while, and as yet there is no counterexample.  follows using topological methods. The conjecture is known when
follows using topological methods. The conjecture is known when 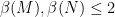 .
.
In the Rota context, this means that even if you take your bases and scramble them – so you no longer have bases, but a collection of n sets of size n, whose union is decomposable into n independent sets, you can cover their union by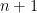 rainbow independent sets. There are examples showing that
rainbow independent sets. There are examples showing that 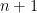 are indeed required in this general case.
are indeed required in this general case.
II. Fair representation. Given a partition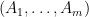 of a set
of a set  , a subset
, a subset  of
of  represents the partition {\em
represents the partition {\em  -fairly} if
-fairly} if 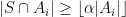 for all
for all 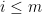 , and {\em almost
, and {\em almost  -fairly} if
-fairly} if 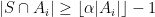 for all
for all 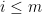 .
. contains an independent set that represents the partition
contains an independent set that represents the partition  -fairly.
-fairly.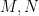 are matroids on the same ground set, then any partition can be represented by an edge of
are matroids on the same ground set, then any partition can be represented by an edge of 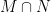 almost
almost  -fairly.
-fairly. – and even this rudimentary case is hard, the proof uses topology. It is known (with a slight weakening) for partitions into two sets.
– and even this rudimentary case is hard, the proof uses topology. It is known (with a slight weakening) for partitions into two sets.
For every partition, a single matroid
A (very bold, I must admit) conjecture is that this is true (well, again almost true) for the intersection of two matroids. Namey, if
This is known (even in a slightly stronger form) for partition matroids with parts of size
III. Rainbow matching: another conjecture of Eli Berger and myself is that given sets of size
sets of size 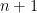 each, all belonging to the intersection
each, all belonging to the intersection 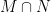 of two matroids
of two matroids  and
and  , then there exists a rainbow set belonging to
, then there exists a rainbow set belonging to 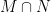 (a rainbow set chooses one element from each of the sets). The special case of
(a rainbow set chooses one element from each of the sets). The special case of 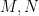 being partition matroids (and then
being partition matroids (and then 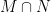 is the matching complex of a bipartite graph) has been studied extensively, with many partial results.
is the matching complex of a bipartite graph) has been studied extensively, with many partial results.
Perhaps some of all this is too daring (in particular, I will not be surprised if II is given a simple counterexample – I haven’t really thought about it for too long). But the phenomenon is intriguing. In particular – is there any connection between these phenomena? Note that in all of them there is a price of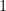 for going from one matroid to the intersection of two matroids. This is reminiscent of Vizing’s theorem, and of the famous Goldberg-Seymour conjecture (and indeed, there is a common generalization of the latter and “I” above).
for going from one matroid to the intersection of two matroids. This is reminiscent of Vizing’s theorem, and of the famous Goldberg-Seymour conjecture (and indeed, there is a common generalization of the latter and “I” above).
Comment by רון אהרוני — February 28, 2017 @ 11:59 am |
Thank you for this enlightening summary. I have a couple of questions about part I. For Rota’s basis conjecture, you say you can prove by topological methods, but conjecture that
by topological methods, but conjecture that  for very general reasons. Why do your current methods fail to do better than
for very general reasons. Why do your current methods fail to do better than  ? Is it because the topological concepts that you are using (connectivity being the main one that I am aware of) are intrinsically too weak to yield a better bound? Or is it that you conjecture that the true values of certain topological invariants are big/small enough to imply
? Is it because the topological concepts that you are using (connectivity being the main one that I am aware of) are intrinsically too weak to yield a better bound? Or is it that you conjecture that the true values of certain topological invariants are big/small enough to imply  , but you are unable to prove that the topological invariants attain the conjectured values?
, but you are unable to prove that the topological invariants attain the conjectured values?
Also, Luke Pebody seems to have given a counterexample to a claim that Eli Berger made above, inside comment #4. Can you comment on that? Does the claim need to be corrected or are we misunderstanding the claim?
Comment by tchow8 — February 28, 2017 @ 9:36 pm |
Ron Aharoni (=רון אהרוני) is giving a lecture about this fascinating topic in Tel Aviv 11 hours from now http://www.math.tau.ac.il/~pelegm/fubtau2017/index.html.
Comment by Gil Kalai — March 4, 2017 @ 9:09 pm |
[…] Polymath 12关注的依旧是一个组合问题:Rota基猜想。和许多组合猜想一样,它的叙述非常、非常简单,只用到一点点的线性代数。 通常我对组合问题的兴趣不大,不过也有例外。早在月旦 I中我们就曾提到,拟阵(matroid)这一概念虽然是组合的,却也容许一个代数几何诠释。近两年颇为热门的「组合(代数)几何」将复代数几何中的正定性定理、Lefschetz-Hodge理论等工具类比地应用于此类组合问题的研究,取得了不少成果。例如,组合几何版的强Lefschetz定理和Hodge-Riemann关系可以用来证明Rota的另一个关于拟阵的猜想: Adiprasito, Huh, Katz Hodge Theory for Combinatorial Geometries 我相信用类似的思路可以解决Rota基猜想。或者说只有这种解答才是「有趣」的。 […]
Pingback by 月旦 XII | Fight with Infinity — February 28, 2017 @ 1:32 pm |
Am I understanding the problem correctly?
We are working in real numbers,
we have a cube of numbers, in depth (front to back) we have representation of a basis vector. Row (left to right) represents basis, meaning every 2D matrix obtained by slicing specific row in depth is a full rank. different basis are stacked vertically (top to bottom). The conjecture states that moving columns, going in depth direction, to left or right we can always obtain a full rank matrix when slicing the cub vertically and in depth (left-most 2D slice is a full rank matrix).
Is this is equivalent?
Comment by mkatkov — February 28, 2017 @ 10:52 pm |
Yes, that is correct. It does not have to be real numbers; the conjecture is that it is true for an arbitrary field. However, it would extremely interesting to prove the conjecture for the reals or for any particular field.
Comment by tchow8 — March 1, 2017 @ 12:16 am |
Just throwing out an idea: a stronger reformulation of this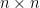 grid might be as a set of
grid might be as a set of  endomorphisms
endomorphisms 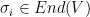 , such that each endomorphism is an isomorphism, and (using
, such that each endomorphism is an isomorphism, and (using  to represent applying
to represent applying  n times) such that each
n times) such that each 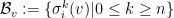 is a basis for every
is a basis for every  . So, the question then becomes proving a statement of there being the desired elements in the endomorphism group. My thought is that if we can find a suitable group
. So, the question then becomes proving a statement of there being the desired elements in the endomorphism group. My thought is that if we can find a suitable group  for which there exists a representation of
for which there exists a representation of  by
by  , then there might be some element of
, then there might be some element of  which “factor into”
which “factor into”  elements which correspond to the transformation desired. I’m not sure under what hypothesis these sorts of things happen, though…
elements which correspond to the transformation desired. I’m not sure under what hypothesis these sorts of things happen, though…
Comment by Juan Sebastian Lozano — March 1, 2017 @ 5:35 am |
Typo: I meant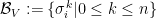
Comment by Juan Sebastian Lozano — March 1, 2017 @ 5:41 am |
This is the wrong notion, the correct notion would be letting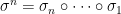 , and then letting
, and then letting  .
.
Comment by Juan Sebastian Lozano — March 1, 2017 @ 5:55 am |
Okay, here is what I think is an equivalent formulation:
Prop: Rota’s conjecture is true if and only if there exists a group such that
such that  is a representation of
is a representation of  and there exists
and there exists 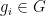 such that
such that 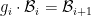 , and for every vector
, and for every vector  $
$ $ where
$ where  and
and  is the identity.
is the identity.
Proof: ( ) The grid will be
) The grid will be 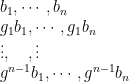
(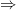 ) Let
) Let 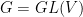 . Let
. Let 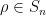 , then
, then 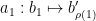 , where
, where  , for every
, for every  , extended linearly. Specifically, we take
, extended linearly. Specifically, we take 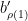 to be the member of
to be the member of 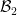 directly below
directly below 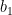 in the grid we know exits according to Rota’s conjecture. Repeating this process for each pair
in the grid we know exits according to Rota’s conjecture. Repeating this process for each pair  we get a set of members of
we get a set of members of  , specifically
, specifically  . Now, letting
. Now, letting 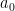 be the identity, we define
be the identity, we define  , which we see means that
, which we see means that 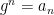 , as desired.
, as desired.
Thanks to Ofir for helping me with formulating this idea: http://math.stackexchange.com/questions/2166516/representations-of-a-group-with-a-set-linearly-independent-factors/2166603#2166603
Comment by Juan Sebastian Lozano — March 1, 2017 @ 2:45 pm |
[…] a completely separate note, here is a new Polymath project that seeks to prove a problem in linear algebra. This is accessible to first-year undergraduates, […]
Pingback by Groups and Group Actions: Lecture 5 | Theorem of the week — March 1, 2017 @ 11:04 am |
Regarding Stone’s formula:
Is there hope to find nice closed formulas (or good asymptotics) for expressions of the form where
where  is small bounded number? especially
is small bounded number? especially  and
and  (maybe
(maybe  ?
?
Comment by Gil Kalai — March 2, 2017 @ 7:10 pm |
I think if k is less than n this sum is 0. Express det(A) in the standard way as a sum of multiples of elements of A and fully expand det(A) ^k. Each term omits some element Aij and so changing the value of that element will keep the term the same and negate the multiplier.
Comment by Luke Pebody — March 2, 2017 @ 8:03 pm |
Since, I think, for every integer p less than n there exists k less than n such that x^n-x^k is always divisible by p, it follows that the Alon-Tarsi difference is divisible by all integers less than n.
Comment by Luke Pebody — March 2, 2017 @ 8:10 pm |
I don’t understand this argument. Suppose for example that k=1. Then det(A) is a sum of n! “monomials” in the Aij, and certainly each individual monomial omits some (in fact, all but n) Aij. But what is “that element” whose value you are changing? Each monomial omits different Aij, and collectively they cover all Aij, so there is no Aij that works uniformly for all monomials. Are you trying to pick a different Aij for each monomial? But then, for each A, you’re pairing it off with n! different matrices, and it’s not obvious to me how to ensure that you’re covering all (matrix,monomial) pairs exactly once.
Comment by tchow8 — March 3, 2017 @ 3:18 am |
is
which is
Now my claim is that for each individual in
in  , this inner sum
, this inner sum 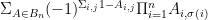 is zero.
is zero. , choose an
, choose an 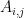 for which
for which 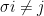 . Then if you change the value of
. Then if you change the value of  , you negate the value of
, you negate the value of
 without changing the value of
without changing the value of 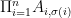 .
.
For this specific
For the more general case of , for each monomial (seen as a function from the elements of A to the integers), you pick an unneeded element
, for each monomial (seen as a function from the elements of A to the integers), you pick an unneeded element 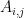 and pair up the matrices that differ only in that
and pair up the matrices that differ only in that 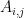 . For this monomial and for each such pair, the product of
. For this monomial and for each such pair, the product of  and the monomial sum to 0. Therefore,
and the monomial sum to 0. Therefore, and the monomial is 0.
and the monomial is 0.
for this monomial and for all matrices, the sum of the product of
Thus the sum over all monomials of the sum over all matrices of this product is 0.
Comment by Luke Pebody — March 3, 2017 @ 3:54 am |
Can we say something about the quantities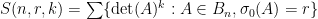 when
when  is an integer
is an integer 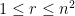 (and
(and  )?
)? are odd is
are odd is  ? And does the negation of Alon Tarski’s conjecture for some even
? And does the negation of Alon Tarski’s conjecture for some even  implies that for every
implies that for every  , and odd $k$ already
, and odd $k$ already  ?
?
In particular, when
Comment by Gil Kalai — March 3, 2017 @ 6:49 am |
When k is odd, S(n, r, k)=0 since swapping the first two rows negates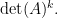
When k is even, S(n, r, k) is the sum of non-negative stuff, so is 0 only when all 0,1 n x n matrices with r 0’s have determinant 0. Probably when r is small or large.
Comment by Luke Pebody — March 3, 2017 @ 7:30 am |
Note that since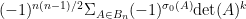 is 0 for all odd
is 0 for all odd  and for all
and for all  , we can replace
, we can replace 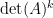 with any degree k+1 polynomial of
with any degree k+1 polynomial of 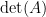 with a non-zero
with a non-zero 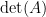 coefficient, if it helps.
coefficient, if it helps.
Comment by Luke Pebody — March 4, 2017 @ 8:06 am |
Several comments related to Rebecca Stones’ formula
The formula identifies the difference as the top Fourier-Walsh coefficient of the function . Since
. Since 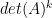 is a polynomial of degree
is a polynomial of degree 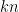 it indeed seems to follow that the top Fourier-Walsh coefficients is o when
it indeed seems to follow that the top Fourier-Walsh coefficients is o when  . Acrually this works also when you replace
. Acrually this works also when you replace 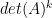 with
with 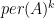 . When
. When 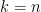 you can compute the top Fourier-Walsh coefficient by adding the contributions of each monomial. Eaxh monomial for $det(A)^n$ corresponds to a generalized diagonal define by a certain permutation. The only monomials that matters are those that involve all the variables and therefore those where the $n$ permutations involved form a Latin square. (If I am not mistaken the contribution is the product of signs of the
you can compute the top Fourier-Walsh coefficient by adding the contributions of each monomial. Eaxh monomial for $det(A)^n$ corresponds to a generalized diagonal define by a certain permutation. The only monomials that matters are those that involve all the variables and therefore those where the $n$ permutations involved form a Latin square. (If I am not mistaken the contribution is the product of signs of the  permutations and I presume (but did not check) that it will give back Rebecca's formula. (Maybe it shows that the corresponding alternating sum for
permutations and I presume (but did not check) that it will give back Rebecca's formula. (Maybe it shows that the corresponding alternating sum for  is non zero but perhaps I missed some signs.)
is non zero but perhaps I missed some signs.)
The second comment is that we have here a question about random Boolean matrices. We would like to understand the behavior of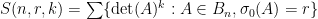 when
when  is even and especially when
is even and especially when  . The obvious conjecture is that the middle term (
. The obvious conjecture is that the middle term (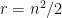 ) dominates the alternating sum. Maybe it is even true (at least for a large
) dominates the alternating sum. Maybe it is even true (at least for a large  ) that the middle term is larger than the sum of all other terms (without the alternating sum).
) that the middle term is larger than the sum of all other terms (without the alternating sum).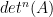 behaves for matrices with
behaves for matrices with  .
.
It would be interesting to guess (even based on a heuristic argument) of the distribution of
The last remark is that perhaps analogs of these questions for random Gaussian matrices are easier (and perhaps even useful). E.g. if we want to understand the spherical harmonics expansion of when
when  is a Gaussian
is a Gaussian  by n matrix.
by n matrix.
Comment by Gil Kalai — March 4, 2017 @ 5:05 pm |
To expand on the last sentence the situation is as follows. We consider a Gaussian random matrix, and the function
matrix, and the function 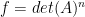 . We can describe this function via the Hermite transform.
. We can describe this function via the Hermite transform.
Let be the normalized Hermite polynomial of degree
be the normalized Hermite polynomial of degree 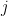 . For
. For 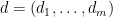 we can define a multivariate Hermite polynomial
we can define a multivariate Hermite polynomial 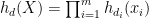 , and the set of such polynomials is an orthonormal basis for
, and the set of such polynomials is an orthonormal basis for  . We can consider the expansion of
. We can consider the expansion of  in terms of Hermite polynomials
in terms of Hermite polynomials 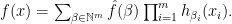 (
(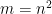 .)
.)
The values are called the Hermite coefficients of
are called the Hermite coefficients of  . The Gaussian analog to Alon-Tarsi’s conjecture is that the Hermite coefficients that correspond to positive vectors of integers are not all zero. (Equivalently, (I think) that the coefficient corresponding to the all 1 vector is non zero.)
. The Gaussian analog to Alon-Tarsi’s conjecture is that the Hermite coefficients that correspond to positive vectors of integers are not all zero. (Equivalently, (I think) that the coefficient corresponding to the all 1 vector is non zero.)
Gaussian random matrices are usually much easier than random Bernoulli (0-1) matrices so maybe the Hermite expansion can be computed precisely. A longer shot would be to try to reduce the Bernoulli case to the Gaussian case via some sort of averaging.
Comment by Gil Kalai — March 4, 2017 @ 9:02 pm |
If we are considering different ways to think about the Alon–Tarsi number, then I think that it is worth studying Theorem 1.9 of Kumar and Landsberg, which gives several reformulations, notably some in terms of an integral over the special unitary group.
Comment by tchow8 — March 5, 2017 @ 10:08 pm |
Yes, indeed there is some similarity with Kumar and Landsberg’s analytical equivalent formulations of the Alon-Tarsi conjecture.
Again, here is my conjecture:
Let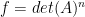 , (
, ( even) then The Hermite coefficient
even) then The Hermite coefficient  for
for  is non zero. (
is non zero. ( is the all one vector.)
is the all one vector.)
Perhaps it would be possible to move between this conjecture and Stones’s Walsh-Fourier formulation of Alon-Tarsi by replacing one by one Boolean rows with Gaussian rows. (But I am not sure at all). Usually Gaussian random matrices are easier compared to Boolean matrices, e.g. we know the joint distribution of eigenvalues (and is the
is the  th power of their product).
th power of their product).
Comment by Gil Kalai — March 6, 2017 @ 6:25 am |
It’s clear we can write down nxn arrays of vectors which “fail Rota” if we drop the hypothesis that each row of the array forms a basis of V; for instance, we could take one of the vectors to be 0. On the other hand, the condition that each row forms a basis is perhaps too strong; e.g. if each row B_i consists of nonzero multiples of a single vector v_i, and the v_1, … v_n are all independent, then the columns form a basis automatically. What is the “right” linear-algebraic/combinatorial condition on the n bases?
Comment by JSE — March 5, 2017 @ 5:32 pm |
Conjecture: For ever , every
, every  -dimensional subspace contains at most
-dimensional subspace contains at most 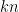 of the
of the 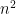 vectors. If true, this would mean that it doesn’t matter how the vectors are arranged. This condition is obviously necessary and for
vectors. If true, this would mean that it doesn’t matter how the vectors are arranged. This condition is obviously necessary and for  also sufficient.
also sufficient.
Comment by domotorp — March 5, 2017 @ 9:01 pm |
This line of thinking is the background behind my “Idea 2.” I believe that Colin McDiarmid’s counterexample works for your conjecture too. Let’s take again but create two copies of the spokes, so the edges are
again but create two copies of the spokes, so the edges are 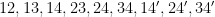 . Then take the rows to be
. Then take the rows to be 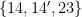 ,
,  , and
, and  . This nine-element matroid is the disjoint union of three bases but you can’t get the columns to all be bases if you are limited to permuting within a row.
. This nine-element matroid is the disjoint union of three bases but you can’t get the columns to all be bases if you are limited to permuting within a row.
Comment by tchow8 — March 5, 2017 @ 9:59 pm |
Right…
Comment by domotorp — March 6, 2017 @ 5:05 am |
Hi all, This is my first post here on RBC and I have been looking up my old work on this which slightly extend my published paper in that SIAM Journal solving the case of n = prime – 1 for characteristics that do not divide n! or n_e-n_0 (number of (reduced) Latin squares of even or odd types respectively). Now I have seen in my notes that it actually also proves, using Cayley’s first hyperdeterminant (I call it det_0) of n^n hypercubes, another result that takes the permanents of the transversals instead of the determinants, but possibly more in a later post.
It has been mentioned that RBC for fields of characteristic two is not solved in many cases yet.
Here is some relation I have with G-C Rota. It was he (and a few others) who first introduced me to matroid theory by giving lectures on it at a conference at Villa Monastero, Lake Como, Northern Italy (early 1980’s). At the time matroid theory was very little known and practised by a few diverse and eccentric people in far out places such as Tasmania and maybe New Zealand (although started by H. Whitney and then W.T. Tutte). Actually Rota was born very close to there in NW Italy. I happen to know that his favourite wine was Asti spumante, which is a speciality of that region in Piemonte, a light and sparkly white wine. He died in 1999 at a young age, but here is a obit from an Italian source that I happen to have translated. It doesn’t mentioned the sometimes controversial books (e.g. Indiscrete Thoughts) and book reviews (in journals that he founded). But here it is:
From the Notices of the Unione Matematica Italiana
(Italian Mathematical Society)
The Death of Prof. Gian-Carlo-Rota
Gian-Carlo-Rota died at the age of 67 years in his house at
Cambridge (Massachussetts). He was the unique lecturer of the
Massachussetts Institute of Technology (MIT) who was Prof. of
Applied Mathematics and also of Philosophy.
He graduated at the University of Princeton and was awarded the
doctorate at Yale under the guidance of Jacob T. Schwartz.
From 1966 up to his death he was a consultant for the Los
Alamos Scientific Laboratory. He was given the title of
Doctor Honoris Causa by the University of Strassburg, France,
in 1984, by the University of Bologna, Italy (1996), and by
Brooklyn Polytechnical University, USA (1997). In 1982 he
was elected member of the National Academy of Sciences and from
1995 to 1997 was vice-president of the American Mathematical
Society (AMS). In 1998 he was “invited presenter” at the
American Mathematical Society Colloquium Lectures: a series of
three talks of increasing complexity presented each year by
more eminent mathematicians in the world. In 1998 he was given
the title of Wiener Professor by MIT.
His research was initially in the direction of operator theory,
differential equations and probability. In the sixties his
interests redirected towards combinatorics and in 1964 he published
“On the Foundations of Combinatorial Theory I: Theory of Moebius
Functions” for which in 1988 he received the prestigious
Steele Prize of the AMS. He was founder of three of the more
prestigious mathematical publications: Journal of Combinatorial
Theory (1966), Advances in Mathematics (1967) and Advances in
Applied Mathematics (1979) and of various series of books such
as Mathematicians of our Time (MIT Press), Contemporary Mathematicians
(Birkhauser Boston) and Encyclopedia of Mathematics (Cambridge
University Press).
Gian-Carlo-Rota is universally held to be the person behind the
transformation of discrete mathematics from a set of unrelated
technical details, each constructed in order to resolve a specific
problem, to a true and proper organic theory, that reveals deep
connections with classical sectors of mathematics and with other
fields of research to which it is traditionally related. In these
last decades, the specialization demanded by research has rendered
more and more arduous the task of whoever wants to establish
connections between various disciplines and even between diverse
sectors of the same discipline. Rota has been one of the rare
people of science who, for the vastness of interests and of his
culture, has known how to move himself with ease and with depth
of thought in fields, even those extremely distant, being able
with that to collect deep analogies between results that are
apparently different.
His premature death is an inestimable loss for comtemporary
mathematics.
D. Senato, M. Barnabei, G.C. Barozzi
Translated by David Glynn
Comment by David Glynn — March 6, 2017 @ 2:47 am |
[…] er lige sat et nyt projekt i søen. Om Rotas basisformodning, som siger følgende: Hvis man har n baser B1,…,Bn for et […]
Pingback by Polymath – matematik i fællesskab online – åbent for alle. | Matematikbloggen på AAU — March 6, 2017 @ 2:50 pm |
I have created a second blog post on this topic. In most cases, further comments should be posted there rather than here. https://polymathprojects.org/2017/03/06/rotas-basis-conjecture-polymath-12-2/
Comment by tchow8 — March 6, 2017 @ 11:22 pm |
[…] conjecture. A similar slightly weaker form of the conclusion of Rota’s basis conjecture is conjectured by Ron Aharoni and Eli Berger in much much greater […]
Pingback by Test Your Intuition about the Alon-Tarsi Conjecture | Combinatorics and more — March 15, 2017 @ 10:29 am |
Hi! are there any news or updates on this project??
Comment by Andreas — April 27, 2017 @ 1:03 pm |
Not much, but the new thread is https://polymathprojects.org/2017/03/06/rotas-basis-conjecture-polymath-12-2/.
Comment by domotorp — April 27, 2017 @ 4:12 pm |
[…] and even then I usually regard it as a positive contribution to the discussion. When I made this remark on poymath12, which turned out to be quite silly a few minutes later, I somehow lost my confidence […]
Pingback by Where were we? | Combinatorics and more — August 24, 2017 @ 5:49 pm |
[…] 12) to solve it. (Here is my post on the project with various variants of the conjecture, the first post on the polymath blog, and the wiki). See this post for several famous conjectures by Rota, and this post about the […]
Pingback by To cheer you up in difficult times 9: Alexey Pokrovskiy proved that Rota’s Basis Conjecture holds asymptotically | Combinatorics and more — August 14, 2020 @ 10:09 am |