I am posting this proposal on behalf of Dinesh Thakur.
Let be the ring of polynomials over the finite field
of two elements, and let
be the set of irreducible polynomials in this ring. Then infinite series such as
and
can be expanded as formal infinite power series in the variable .
It was numerically observed in http://arxiv.org/abs/1512.02685 that one appears to have the remarkable cancellation
and
For instance, one has
and all other terms in are of order
or higher, so this shows that
has
-valuation at least 3. Similarly, if one expands the first sum for all primes of degree (in
) up to 37, one obtains
(the calculation took about a month on one computer), implying that the
-valuation of the infinite sum is at least 38; in fact a bit of theory can improve this to 42. (But we do not know whether this 42 is the answer to everything!).
For the second sum, calculation for degrees up to 28 shows that the difference between the two sides has -valuation at least 88.
The polymath proposal is to investigate this phenomenon further (perhaps by more extensive numerical calculations) and supply a theoretical explanation for it.
Background links:
- The paper http://arxiv.org/abs/1512.02685 where these (and many more guesses of this type) are given with some background on zeta deformation etc, and
- http://www.math.rochester.edu/people/faculty/dthakur2/primesymmetryrev.pdf where the updated version is and will be maintained.
Below the fold is some more technical information regarding the above calculations.
To show how complicated the cancellations are we record triples with degree , then
-power for the first sum for degree
primes followed by the
-valuation
[…] on the polymath blog, I’ve posted (on behalf of Dinesh Thakur) a new polymath proposal, which is to explain some numerically observed identities involving the irreducible polynomials in […]
Pingback by A new polymath proposal: explaining identities for irreducible polynomials | What's new — December 28, 2015 @ 7:40 pm |
What happens for other characteristics?
Comment by Joshua Zelinsky — December 28, 2015 @ 10:56 pm |
What’s the fastest way to find irreducible polynomials over F_2? Presumably there’s something smarter than the sieve of Eratosthenes…?
Comment by Dustin G. Mixon — December 28, 2015 @ 11:43 pm |
Just factor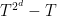 using Berlekamp’s algorithm.
using Berlekamp’s algorithm.
Comment by Ofir Gorodetsky — December 29, 2015 @ 5:26 am |
As mentioned above, it’s not clear that this is the best method for reasons of space. Enumerating polynomials one at a time takes space O(d), whereas to write down the full factorization of t^(2^d)-t will require something more like O(2^d) space. It would be better to have a fast irreducibility = primality test.
Comment by John Voight — December 29, 2015 @ 8:57 pm |
I believe the fastest way to find irreducible polynomials, factor, or do modular composition over F_2 would be in the recent Kedlaya-Umans work: http://users.cms.caltech.edu/~umans/papers/KU08-final.pdf
This might lend itself to some additional efficiencies over and above finding the irreducible polynomials.
Comment by John Nicol — December 30, 2015 @ 12:59 am |
I believe I understand why the three lines of TeX which do not currently parse are not currently parsing. There are additional spaces in the TeX (which of course compile perfectly fine in LaTeX but which the WordPress Plugin cannot handle). For one particular example, I believe there is an additional space after the comma after the first paren-group (9, 12, 10) in the first formula which does not compile. [Please forgive me if I’m wrong — there is some guesswork as I don’t see the actual source].
[That seemed to fix the parsing errors for those three lines, though I’m still having trouble getting some other LaTeX code to parse at all. Will keep trying – T.]
Comment by David Lowry-Duda — December 29, 2015 @ 4:20 am |
I intend to check later the following sum – sum_(P monic irreducible in F_q[T]) 1/(1-P^(q-1)). The summand can also be written as sum(a in F_q*) 1/(1-aP), which generalizes the F2 case (but might be completely wrong generalization…). I’ll have time only a day from now, so if someone wants to do it, that would be great.
Comment by Ofir Gorodetsky — December 29, 2015 @ 5:33 am |
https://s0.wp.com/latex.php?latex=%28%5Csum_%7BP+%5Cin+%7B%5Cmathcal+P%7D%3A+%5Chbox%7Bdeg%7D%28P%29+%5Chbox%7B+odd%7D%7D+%5Cfrac%7B1%7D%7B1%2BP%7D%29+%28%5Csum_%7BQ+%5Cin+F_2%5Bt%5D%3A+Q+%5Cneq+0%7D+%5Cfrac%7B1%7D%7BQ%7D%29+%3D+%5Csum_%7BQ+%5Cin+F_2%5Bt%5D%3A+Q+%5Cneq+0%2C+%5Chbox%7Bdeg%7D%28Q%29+%5Chbox%7B+odd%7D%7D+%5Cfrac%7B1%7D%7BQ%7D&bg=ffffff&fg=000000&s=0
Comment by sdsd — January 21, 2019 @ 12:45 pm |
This doesn’t seem to directly help much with the original problem, but there is the identity
arising from the fact that the number of odd-degree irreducible polynomials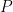 dividing a given non-zero polynomial
dividing a given non-zero polynomial 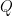 (counting multiplicity) will have the same parity as the degree of that polynomial, thanks to the fundamental theorem of arithmetic in
(counting multiplicity) will have the same parity as the degree of that polynomial, thanks to the fundamental theorem of arithmetic in ![F_2[t]](https://s0.wp.com/latex.php?latex=F_2%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) . In principle this should let one compute the odd-degree component of
. In principle this should let one compute the odd-degree component of  . I don’t know how to deal with the even-degree component though.
. I don’t know how to deal with the even-degree component though.
Comment by Terence Tao — December 29, 2015 @ 5:35 am |
This looks like a very nice project! If turned into a full project this will be (I think) the first time that we have more than one polymath project running in parallel and this is very welcomed! Right now polymath10 devoted to the Erdos-Rado sunflower conjecture is running in my blog; Here is the link to the first post. It is possible that yet another polymath project will take place over a third blog in the coming months.
Comment by Gil Kalai — December 29, 2015 @ 6:00 am |
This seems like a nice project. It also seems amenable to some early direct computation, which I think has served past polymath projects well.
I wonder if there is a nice way to parallelize construction of irreducible polynomials up to degree d. Or more simply, is there a good way to construct irreducible polynomials of degree d+1 without constructing irreducible polynomials of degree d? One conceivable answer might be to run Berlekamp’s Algorithm (as mentioned by Ofir above) on . I do not know the implementation or running time of Berlekamp’s Algorithm to know whether or not this would save time or merely add to it.
. I do not know the implementation or running time of Berlekamp’s Algorithm to know whether or not this would save time or merely add to it.
Comment by David Lowry-Duda — December 29, 2015 @ 6:58 am |
The triple for d=14 is missing. Judging by d=13 and 15, it ought to be (14,14,16).
Comment by Dustin G. Mixon — December 29, 2015 @ 11:30 am |
Yes, the missing triple is (14,14,16).
Comment by John Voight — December 29, 2015 @ 8:53 pm |
I vaguely remember that there are some nice formulas and nice related combinatorics for the product of all irreducible polynomials of a given degree (namely you can derive it by either using a little more Galois theory, or a little more generating functions machinery).
Comment by Gil Kalai — December 29, 2015 @ 6:42 pm |
Gil, you remember correctly. If you denote by P_n the product of the monic irreducibles of degree n in F_q[T], then the product of P_d over d dividing n is T^(q^n)-T (consequence of F_(q^n) being a field containing exactly the roots of all these polynomials, and of Lagrange’s Theorem). Now apply Mobius inversion and get: P_n = prod(d | n) (T^(q^n)-T)^(mobius(n/d)). This can be simplified further (for instance, once can replace T^(q^n)-T with T^(q^n – 1)-1 ).
Comment by Ofir Gorodetsky — December 29, 2015 @ 7:51 pm |
Consider the generating function where
where  runs over all monic polynomials over
runs over all monic polynomials over 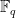 and
and  denotes the number of irreducible factors (with multiplicity) of
denotes the number of irreducible factors (with multiplicity) of  (not the degree). It has an Euler product factorization
(not the degree). It has an Euler product factorization
where the product runs over monic irreducible polynomials over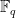 . Taking the logarithmic derivative with respect to
. Taking the logarithmic derivative with respect to  gives
gives
Maybe someone can do something with this.
Comment by Qiaochu Yuan — December 29, 2015 @ 9:48 pm |
This is certainly an interesting manipulation, but the logarithmic derivative seems to be missing a factor of P(t) in the numerator. Also, if one tries to calculate the coefficient of z in the generating function zeta, one encounters an infinite sum of irreducible polynomials, and I don’t see any straightforward way to make sense of that sum.
Comment by Partha Solapurkar — December 29, 2015 @ 11:40 pm |
Nuts, you’re right. Fortunately, the two expressions differ by a constant, namely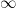 ! And yes, this is an entirely formal manipulation; I haven’t thought about what kind of convergence even in the sense of formal power series we have.
! And yes, this is an entirely formal manipulation; I haven’t thought about what kind of convergence even in the sense of formal power series we have.
Comment by Qiaochu Yuan — December 30, 2015 @ 1:03 am |
It’s OK if we use instead, because there are finitely many
instead, because there are finitely many 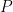 of any given (positive) degree, and we’re working with power series in
of any given (positive) degree, and we’re working with power series in  . Actually, this is (essentially) the approach discussed at the beginning of the original article (http://arxiv.org/pdf/1512.02685v1.pdf).
. Actually, this is (essentially) the approach discussed at the beginning of the original article (http://arxiv.org/pdf/1512.02685v1.pdf).
Comment by Victor Wang — December 30, 2015 @ 1:15 am |
My first thought is to rearrange the sum as

 is the set of perfect powers of irreducible polynomials. Then I might group the latter sum by the degree of
is the set of perfect powers of irreducible polynomials. Then I might group the latter sum by the degree of 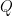 . Does this go anywhere?
. Does this go anywhere?
where
Comment by David Speyer — December 29, 2015 @ 10:07 pm |
Talking with John Voight, here’s a brief description of his computation (the results that Terry Tao summarized above):
He uses Magma to test each polynomial of degree n for irreducibility, and then if the polynomial is irreducible, he computes the corresponding power series to precision 45 (ignoring u^46 and above) and adds it to the running total. Overall, this takes 2^(n-1) iterations, and testing irreducibility costs soft-O(n^2) operations (presumably, this is the bottleneck of each iteration).
For reference, it took 19 days to perform these iterations for degree n=37. At this rate, we can expect the degree-38 calculation to take well over a month. By the “prime number theorem” for F_2, there are about 2^(n-1) irreducible polynomials of degree n, and so we’re stuck with exponential time unless we can avoid listing all irreducible polynomials.
Comment by Dustin G. Mixon — December 30, 2015 @ 12:47 am |
Correction: There are about (2^n)/n irreducible polynomials of degree n.
Comment by Dustin G. Mixon — December 30, 2015 @ 12:55 am |
Yep, it seems this could be optimized via Kudlaya-Umans. Their algorithm indicates improving irreducibility testing (via Rabin’s test) to more like O~(n log n) operations, for small fixed characteristic.
Comment by John Nicol — December 30, 2015 @ 1:39 am |
Is there an existing implementation of Kudlaya-Umans? I wonder how big the hidden constant is. (They improve upon an alternative whose time complexity involves the omega from matrix multiplication, so that’s a red flag…)
Comment by Dustin G. Mixon — December 30, 2015 @ 1:47 am |
I can’t find one online. According to some comments I’ve found in other papers, the constant probably swamps the algorithm with degrees this low.
Not sure what the Magma application is doing under the covers for finite-field-polynomial irreducibility testing, as it’s closed-source — is it known to be efficient, even O(N^2), for this particular operation?
Comment by John Nicol — December 30, 2015 @ 2:33 am |
The obvious test is to run IsIrreducible(f) for random polynomials f of various degrees and observe how the runtime scales. Perhaps an existing Magma-user will run the experiment? If not, I’ll download Magma and run it myself.
Comment by Dustin G. Mixon — December 30, 2015 @ 3:15 am |
I’m trying to figure out if the product formula for the Carlitz exponential is useful. (I usually would think about this sort of thing longer before posting it, but my understanding is that the etiquette of Polymath’s is to post half baked ideas.) A good reference is the book chapter here. In particular, see Theorem 3.2.8 and the material before it. I’ll summarize:
Let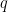 be a prime power. Put
be a prime power. Put ![[i] = T^{q^i}-T](https://s0.wp.com/latex.php?latex=%5Bi%5D+%3D+T%5E%7Bq%5Ei%7D-T&bg=ffffff&fg=000000&s=0&c=20201002) and
and ![D_i = [i] [i-1]^q [i-2]^{q^2} \cdots [1]^{q^{i-1}}](https://s0.wp.com/latex.php?latex=D_i+%3D+%5Bi%5D+%5Bi-1%5D%5Eq+%5Bi-2%5D%5E%7Bq%5E2%7D+%5Ccdots+%5B1%5D%5E%7Bq%5E%7Bi-1%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Put
. Put  . This is
. This is 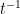 -adically convergent for any
-adically convergent for any  in
in 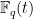 . Then we have
. Then we have
where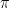 is a certain transcendent power series in
is a certain transcendent power series in 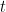 , which can be found by comparing powers of
, which can be found by comparing powers of 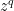 .
.
The problem, of course, is that the product is over all nonzero polynomials, not just the irreducible ones. Comparing coefficients of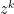 on both sides gives some interesting identities though. For example, taking
on both sides gives some interesting identities though. For example, taking 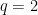 and comparing powers of
and comparing powers of  , we get
, we get
where the sum is over unordered pairs of distinct nonzero polynomials in
of distinct nonzero polynomials in ![\mathbb{F}_2[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Putting
. Putting  , we can rewrite this as
, we can rewrite this as
where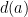 is the number of divisors of
is the number of divisors of  .
.
Now,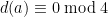 unless
unless  is a square or a prime times a square. So this sum isn’t so far from being a sum over primes …
is a square or a prime times a square. So this sum isn’t so far from being a sum over primes …
That’s how far I’ve gotten so far.
Comment by David Speyer — December 30, 2015 @ 1:28 am |
I believe I have a proof. Let be the set of nonzero polynomials in
be the set of nonzero polynomials in ![\mathbb{F}_2[x]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) . For any set
. For any set  , let
, let  be the set of unordered pairs of distinct elements of
be the set of unordered pairs of distinct elements of  . As explained above, looking at the coefficient of
. As explained above, looking at the coefficient of  in the product term for the Carlitz exponential shows that
in the product term for the Carlitz exponential shows that
We can factor this as
Computing the first term up to order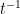 shows that it is nonzero, so
shows that it is nonzero, so
Let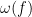 be the number of distinct irreducible factors of
be the number of distinct irreducible factors of  . Then the number of ways to factor
. Then the number of ways to factor  as
as 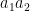 with
with  is
is 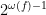 (or
(or  if
if  .) Since we are working modulo
.) Since we are working modulo  , the only terms which contribute to the sum are powers of irreducible polynomials. We obtain
, the only terms which contribute to the sum are powers of irreducible polynomials. We obtain
The inner sum is a geometric series, and we have
as desired.
Comment by David Speyer — December 30, 2015 @ 10:40 am |
Dear David, This is very nice!
Comment by Gil Kalai — December 30, 2015 @ 11:23 am |
I was rather confused by the phrase “Computing the first term up to order t^(-1)”. I get it now: By “term” you mean “factor”.
Comment by Dustin G. Mixon — December 30, 2015 @ 4:22 pm |
Wow, this is very nice! So it seems the general strategy is (a) to express sums over irreducible polynomials in terms of sums over all polynomials, by a finite characteristic version of “multiplicative number theory”, and then (b) to use the Carlitz product formula (or related machinery) to evaluate the resulting sums over all polynomials. The Carlitz stuff is new to me, this is something I will definitely try to learn more about (though not immediately, due to various holiday activities).
Looks like this Polymath project is almost wrapping up before it even officially started… but I guess that’s a good “problem” to have.
Comment by Terence Tao — December 31, 2015 @ 3:56 pm |
Building on the ideas in my previous post, I can show that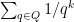 is in
is in 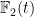 for any positive integer
for any positive integer  , where
, where 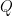 is the set of powers of irreducible polynomials in
is the set of powers of irreducible polynomials in ![\mathbb{F}_2[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Once again, let
. Once again, let  be the set of nonzero polynomials in
be the set of nonzero polynomials in ![\mathbb{F}_2[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
. be the fraction field
be the fraction field 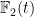 ,
,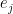 be the
be the 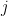 -th elementary symmetric polynomial and let
-th elementary symmetric polynomial and let  .
.
Let
let
Lemma 1: For any positive integer , we have
, we have 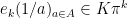 .
.
Proof: Look at the coefficient of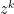 in
in  , where
, where  is the Carlitz exponential.
is the Carlitz exponential.
Lemma 2: Let be any symmetric polynomial of degree
be any symmetric polynomial of degree  with integer coefficients. Then
with integer coefficients. Then 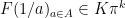 .
.
Proof: The ring of symmetric polynomials is generated by the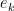 .
.
Lemma 3: The fraction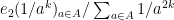 is in
is in  .
.
Proof: By Lemma 2, the numerator and denominator are in . (And the denominator is nonzero, as every term except
. (And the denominator is nonzero, as every term except  has no constant term.)
has no constant term.)
The fraction in Lemma 3 is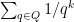 by the same argument I used in the
by the same argument I used in the  case. QED
case. QED
If we replace![\mathbb{F}_2[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_2%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) by
by ![\mathbb{F}_{2^j}[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_%7B2%5Ej%7D%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) , the same method should work if
, the same method should work if  ,
, 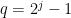 . Without this condition, the ratio in Lemma 3 is
. Without this condition, the ratio in Lemma 3 is 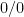 .
.
No ideas about odd characteristic yet.
I’m going to take a break from this for the rest of the day. Others are welcome to join in!
Comment by David Speyer — December 30, 2015 @ 6:07 pm |
The above should read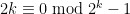 , which is, of course, equivalent to
, which is, of course, equivalent to  . [Corrected, – T.]
. [Corrected, – T.]
Also, I am not taking a break, because I just figured out how to attack odd characteristic.
Comment by David Speyer — December 30, 2015 @ 7:02 pm |
Let be a prime,
be a prime,  a power of
a power of  . Let
. Let  be the nonzero polynomials in
be the nonzero polynomials in ![\mathbb{F}_r[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_r%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) , and let
, and let 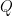 be the powers of the irreducible ones (not assumed monic). The point of this post is to discuss computing
be the powers of the irreducible ones (not assumed monic). The point of this post is to discuss computing 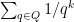 is in
is in  . If
. If 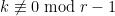 , the sum is
, the sum is 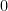 by grouping together scalar multiples of the same polynomial, so we may and do henceforth assume
by grouping together scalar multiples of the same polynomial, so we may and do henceforth assume  .
.
As before, let be the nonzero polynomials in
be the nonzero polynomials in ![\mathbb{F}_r[t]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_r%5Bt%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Let
. Let 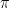 be a
be a  -st root of
-st root of  in
in 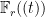 . Let
. Let  .
.
Lemma 1: If is a degree
is a degree  symmetric polynomial with integer coefficients, then
symmetric polynomial with integer coefficients, then  is in
is in  .
.
Proof: As before.
Lemma 2: With our assumption that , we have
, we have  .
.
Proof: The only summands with constant terms are from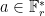 , and that sum is
, and that sum is  .
.
Let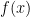 be the symmetric polynomial
be the symmetric polynomial  . Note that
. Note that  has integer coefficients. So, by the lemmas,
has integer coefficients. So, by the lemmas, 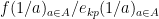 makes sense and is in
makes sense and is in  .
.
Expanding this out and factoring out GCD’s, this ratio is
where the sum is over ordered -tuples with
-tuples with  and the
and the 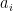 not all equal, and the division by
not all equal, and the division by  must be interpreted as grouping together terms which are rotations of each other. (The condition that the
must be interpreted as grouping together terms which are rotations of each other. (The condition that the 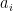 are not all equal just discards
are not all equal just discards 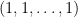 .)
.)
This is , where
, where  is the number of ways to factor
is the number of ways to factor  as
as  with
with  . Again, we must compute
. Again, we must compute  as an integer before reducing it to characteristic
as an integer before reducing it to characteristic  .
.
Up to a nuisance power of , we can easily see that
, we can easily see that  is a multiplicative function of
is a multiplicative function of  . If
. If 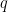 is irreducible, then
is irreducible, then  is the number of ways to write
is the number of ways to write 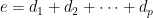 , with the
, with the 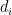 nonnegative integers and
nonnegative integers and  . This set has a free action of the cyclic group of order
. This set has a free action of the cyclic group of order  by rotating the
by rotating the 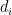 , so
, so  is divisible by
is divisible by  . Thus, if
. Thus, if  is not a prime power, then
is not a prime power, then  and doesn’t contribute to the sum
and doesn’t contribute to the sum
Thus, as before, we are left just summing over prime powers, although this time the sum depends on the exponent in the prime power in a more complicated way.
I’ve promised my daughter to read her a story now, so I’m stopping here.
Comment by David Speyer — December 30, 2015 @ 7:38 pm |
To finish up this note — Let be the number of ways to write
be the number of ways to write  with all
with all  and
and 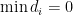 . I believe the argument above shows that
. I believe the argument above shows that
is in . If I did the combinatorics right, I get two simpler formulas: I think this is also
. If I did the combinatorics right, I get two simpler formulas: I think this is also
and
where
So, where does this go? Are there people besides me who want to think about this? What is left to be done?
Comment by David Speyer — December 31, 2015 @ 12:00 am |
Because of the zeta connection, I expected `something’ for any q.For odd characteristic, when the same thing did not seem to work numerically, I had tried a few simple linear
combinations (one very close to the second displayed formula in this note), but it did not work
without the proper circle of ideas that David has introduced!
Comment by Dinesh S Thakur — December 31, 2015 @ 12:43 am |
Excellent David! Your proofs generalize to class number one higher genus A’s with rational infinite
place and p=2 immediately (there are 4 of them without char. restriction, at least 2 or 3 in char. 2) and probably even more, with more work! May be somebody will see how to put characters and get algebraic things in more generality still.
These were the most interesting conjectures to me personally, but the preprint link has many more guesses/numerical observations at finite level which are still open and will need different methods to attack. Polymath community hopefully will settle them soon too. Thanks!
I just traveled to India, so unfortunately cannot edit and update (till 13th Jan) my webpage link as promised.
Sorry.
Comment by Dinesh S Thakur — December 31, 2015 @ 12:16 am |
Minor additional comments: Settling `vanishing’ part of conjectures (for example, the
simplest case is vanishing for q=2^n, k=q-1, which follows easily by David’s proof in 14 applied to the
product of scalar multiples (q-1 of them) of a monic polynomial), characterization of vanishing,
explicit formulae for rationality, various conjectural or unknown results on prime power sums valuations
and vanishing (many examples in preprint) are some areas where polymath talent can help in many ways.
(I should say that I have not done thorough checks on these parts of conjectures and some are
wild speculations, so it might be good to test them numerically much better to see whether they survive before serious attempt to prove!).
There are also transcendence proving aspects when rationality or algebraically is not seen. (See preprint).
Most exciting would be discovering some rationality/algebraicity in number fields prime sums of certain kind,
by taking some clues from here. I only want to say that when I tried this numerically, I did get some surprising `close encounters’ (but not exact) and it might still be just possible!
Comment by Dinesh S Thakur — December 31, 2015 @ 2:11 am |
Congratulations to David Speyer for proving a big chunk of Dinesh’s conjecture!
In case there’s still a need to efficiently sum over degree- irreducibles
irreducibles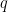 -element field
-element field  :
:
over a
Fix a convenient model of a degree- extension
extension  of
of  , and a generator
, and a generator
 of
of 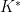 . (We don’t mind spending a good amount of time finding this
. (We don’t mind spending a good amount of time finding this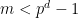 such that for each
such that for each 
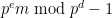 strictly exceeds
strictly exceeds  : such
: such 
 , namely
, namely
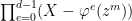 where
where 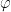 is the
is the
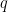 -power Frobenius. This should also be reasonably straightforward
-power Frobenius. This should also be reasonably straightforward
data because we need do it only once.) Then the irreducibles are in 1:1
correspondence with positive
the remainder of
corresponds to the minimal polynomial of
to parallellize.
Comment by Noam D. Elkies — December 31, 2015 @ 5:11 am |
[…] Anna continues her investigation of irreducible polynomials over the finite field with 2 elements. In this installment, she works out the roots of all the irreducible polynomials of degrees 4 and 5. Anna’s entire investigation traces back to an exercise suggested by Prof. Judy Walker in her interview from Volume 8, Number 6. Do you think you can see where Anna might be headed? If you do, follow your thoughts and see where they lead. You’re invited to tell us about it; we’d love to hear from you. If you’re falling in love with polynomials over , check out this proposal for a new PolyMath project and the comments that follow. […]
Pingback by Girls’ Angle Bulletin, Volume 9, Number 2 | Girls' Angle — December 31, 2015 @ 5:06 pm |
Just a remark: one only needs a small portion of the theory of the Carlitz exponential to run David’s argument in 14, one just needs to play with Moore matrices. For any degree , observe from the linearity of the Frobenius map
, observe from the linearity of the Frobenius map 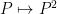 that the vector
that the vector 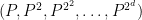 is a linear combination of the vectors
is a linear combination of the vectors 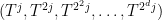 for
for  whenever
whenever 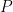 is a polynomial in
is a polynomial in ![F_2[T]](https://s0.wp.com/latex.php?latex=F_2%5BT%5D&bg=ffffff&fg=000000&s=0&c=20201002) of degree at most
of degree at most 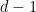 (we include the case
(we include the case  here). Therefore, the Moore determinant
here). Therefore, the Moore determinant
vanishes whenever is a polynomial of degree at most
is a polynomial of degree at most 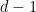 , giving
, giving  distinct roots to this determinant. On the other hand, this determinant is clearly a polynomial in
distinct roots to this determinant. On the other hand, this determinant is clearly a polynomial in  (with coefficients in
(with coefficients in ![F_2[T]](https://s0.wp.com/latex.php?latex=F_2%5BT%5D&bg=ffffff&fg=000000&s=0&c=20201002) ) of degree
) of degree  . Thus, by the factor theorem, this determinant must equal a non-zero scalar multiple of
. Thus, by the factor theorem, this determinant must equal a non-zero scalar multiple of 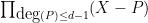 . On the other hand, the
. On the other hand, the 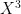 coefficient of the determinant is clearly zero. Therefore the
coefficient of the determinant is clearly zero. Therefore the 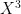 coefficient of
coefficient of 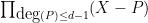 vanishes, and hence the
vanishes, and hence the  coefficient of
coefficient of 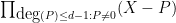 vanishes. Dividing by the non-zero quantity
vanishes. Dividing by the non-zero quantity 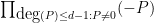 , we conclude that
, we conclude that
where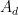 is the set of non-zero polynomials of degree less than or equal to
is the set of non-zero polynomials of degree less than or equal to 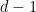 . Sending
. Sending  , we obtain the identity
, we obtain the identity
that David used to prove the identity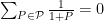 .
.
Comment by Terence Tao — January 1, 2016 @ 7:25 pm |
This gives a nice proof that for some sequence
for some sequence 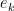 . The further fact which I need in the later parts is that there is a series
. The further fact which I need in the later parts is that there is a series 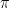 such that
such that 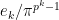 is in
is in  . Can you get that out of this?
. Can you get that out of this?
Comment by David Speyer — January 1, 2016 @ 10:37 pm |
Yes, 14 needs only F_q linearity, and both that and the general fact needed with explicit pi (needs just a little more manipulation) as you mentioned were derived by Carlitz in his 1935 paper using exactly this
Moore determinant technology and independently (without explicit formulas but in great generality) was achieved similarly again in Drinfeld’s 1974 paper. (There are expositions and variants
in Goss’ and my books.)
Not relevant here, but historically interesting fact is that
some of the `higher rank Drinfeld modules theory was also developed by
Carlitz (unpublished) and those `lecture notes’ were published by his student Hayes in Finite Fields and their applications special issue on carlitz.
Comment by Dinesh S Thakur — January 2, 2016 @ 12:07 pm |
Hi,
Very interested outsider here! Feel free to moderate out this comment if it is inappropriate, but this result seems incredible and raises many questions, including:
1) What are the implications of finding this structure among the irreducible polynomials over F2? Are the implications limited because of being over F2 and because of being polynomials?
2) Is there likely to be any structure at all among the interaction terms? If so/not, what are the implications?
3) The prime numbers are often treated as if they are distributed randomly. Is there any sense in which the terms in this problem are considered to be distributed randomly, and if so, what does the “vanishing” mean in this context?
4) Are there any immediate or indirect consequences for sums over the integers (in particular over the prime numbers)? I’m guessing not, but is there possibly a field and a formula for which the primes vanish?
5) Again back to the randomness question, and still not quite understanding how the distribution of irreducible polynomials would be represented, does a result like this have any implications for separating pseudo-random sequences from truly random sequences?
Comment by Ian Finn — January 2, 2016 @ 4:04 am |
This sounds like an interesting discussion. I wish I had gotten to it a little earlier, so I could follow along better. The main thought I had was that some irreducible polynomials might be equivalent under different primes.
Comment by Jesse — January 4, 2016 @ 2:18 pm |
At this point, I could either imagine this becoming a short project or a much longer one. The short version contains the proofs above, and also explicitly computes many of the sums. I would imagine the scope of that paper being![\mathbb{F}_q[T]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_q%5BT%5D&bg=ffffff&fg=000000&s=0&c=20201002) for an arbitrary
for an arbitrary 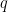 .
.
If it were to become much longer, here are two things which might be worth trying, and that I don’t intend to think about:
(1) Prof: Thakur points out to me via e-mail that the proofs also work for class number one higher genus A’s with one rational infinite place. That doesn’t seem like an interesting enough generalization to me to be worth putting as more than a remark. More interesting would be to get to higher genus A’s with one rational infinite place. The problem is that we want to sum over all maximal ideals, and some of them are not principal. But, we could look for formulas for sums like . Here
. Here  is the maximal ideals of
is the maximal ideals of  and
and  is a rational function and
is a rational function and 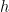 is the class number. We interpret
is the class number. We interpret  as meaning any generator of the principal ideal
as meaning any generator of the principal ideal  . Any two such generators differ by an element of
. Any two such generators differ by an element of  , so
, so  is well defined.
is well defined.
(2) It would be worth checking whether there are more rational identities to be found, which are not obvious consequences of the above. For example, set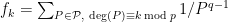 . Are any
. Are any 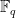 -linear combinations of the
-linear combinations of the  rational, other than
rational, other than 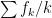 ? (We could search for this using continued fractions.) More generally, we could look for a linear relation
? (We could search for this using continued fractions.) More generally, we could look for a linear relation  with
with 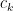 in
in  . (Is there some sort of LLL algorithm for
. (Is there some sort of LLL algorithm for ![\mathbb{F}_q[T]](https://s0.wp.com/latex.php?latex=%5Cmathbb%7BF%7D_q%5BT%5D&bg=ffffff&fg=000000&s=0&c=20201002) ?)
?)
After all, I just came up with the first symmetric function I could think of to extract the irreducible polynomials; there may be many others.
Comment by David Speyer — January 5, 2016 @ 9:07 pm |
(3) We might as well check that nothing happens if you sum over just the monic representatives of the irreducible polynomials. That’s what I’d expect, based on the analogy to the function, but I wouldn’t have guessed these formulas if I hadn’t seen them either.
function, but I wouldn’t have guessed these formulas if I hadn’t seen them either.
Comment by David Speyer — January 6, 2016 @ 1:49 am |
(1) Getting more relations of this type showing new symmetries in prime distribution sounds like the top priority and most suitable for polymath, as different people can check different things (I had tried some linear combinations without success, and meant such things when `putting in characters’ was mentioned!). (2) Characterization of vanishing (rather than
only rationality) and explicit formula families (as in k=2^n-1 part of conj. B) would be very interesting. Again diffferent
people can work on different parts (different q’s for example, checking last part of conjecture C, which is a little
wild, but very effective. If true, proving it would be very nice! Cleaner combinatiorial characterization for that part
would also be very nice. ). (3) As for class no. 1, it is a remark since David’s beautiful proofs work straight (I had numerical evidence, but not solid), without which it was unclear whether it was rational function field phenomena or more.
Comment by Dinesh S. Thakur — January 6, 2016 @ 4:09 am |
I’ve put up a draft paper explaining the results I sketched above at http://www.math.lsa.umich.edu/~speyer/PolymathIdentities.pdf . Comments, large and small, are very welcome.
Obviously, it still needs some editing to be arXiv ready (and shortly thereafter, submission ready), but I mostly want to get this off of my to-do list soon. This paper also shows how far I want to go with this as a research project. If someone out there has cool ideas beyond what I’ve written, they are very welcome to pursue them, and I won’t compete with them.
As you can see, I am planning to make this a solo paper (with Terry and Dinesh’s permission). I hope no one will feel cheated by that, it seems reasonable to me.
Comment by David Speyer — January 11, 2016 @ 7:30 pm |
I just looked at this. Can you write down the derivation of anyway? Even though you have proven something more general. What are some examples of
anyway? Even though you have proven something more general. What are some examples of 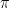 in your function field? It just says all coefficients “match”
in your function field? It just says all coefficients “match”
Comment by John Mangual — January 18, 2016 @ 2:54 pm |
I didn’t think the paper was interesting enough to be worth writing up the p=2 case separately, but you can see it as my December 30, 2015 @ 10:40 am post above. Comparing coefficients of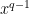 , we have
, we have 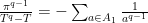 , where
, where 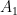 is the monic polynomials. (This is analogous to defining the archimedean
is the monic polynomials. (This is analogous to defining the archimedean 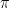 by
by 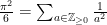 .
.
Comment by David Speyer — January 19, 2016 @ 2:41 pm |
Interesting to whom? Certainly we are all here because we found this problem (kind of) interesting. Personally I find lots of things interesting and fall into the trap of assuming other people will be interested as well.
Actually… not in any rush here. For now, I am content reading your comments and just knowing that p=2 case is true.
Comment by John Mangual — January 19, 2016 @ 6:20 pm |
I think it should be a solo paper. You have already included an appropriate acknowledgement section. I would try to avoid the unfortunate alliteration/homophones “Some sums” though…
Comment by sdf — January 13, 2016 @ 12:42 pm |
[…] on the polymath blog, I’ve posted (on behalf of Dinesh Thakur) a new polymath proposal, which is to explain some numerically observed identities involving the irreducible polynomials in […]
Pingback by A new polymath proposal: explaining identities for irreducible polynomials | TRIFORCE STUDIO — January 20, 2016 @ 5:23 am |
[…] very nice polymath proposal by Dinesh Thakur was posted by Terry Tao on the polymath blog. The task was to explain some […]
Pingback by News (mainly polymath related) | Combinatorics and more — January 20, 2016 @ 6:22 am |
[…] question of whether to call it Polymath11 (the first unclaimed number) or Polymath12 (regarding the polynomial-identities project as Polymath11). In the end I’ve gone for Polymath11, since the polynomial-identities project […]
Pingback by FUNC1 — strengthenings, variants, potential counterexamples | Gowers's Weblog — January 29, 2016 @ 2:41 pm |
[…] beautiful polymath proposal by Dinesh Thakur was posted by Terry Tao on the this blog. The task was to explain some […]
Pingback by Explaining Polynomials Identities – Success! | The polymath blog — February 7, 2016 @ 3:03 am |
The last update is nearly two months old. I wonder whether David’s paper is already on arxiv or submitted? I couldn’t find anything on arxiv. thanks!
Comment by Timmon Spear — April 4, 2016 @ 9:15 pm |
Thakur updated his article on this with Speyer’s argument: http://arxiv.org/abs/1512.02685
Comment by Terence Tao — April 4, 2016 @ 9:51 pm |
Further updates are and will be at my webpage at the link mentioned in the arxive version. Anybody who knows of or makes further progress is
requested to let me know. Thanks! —Dinesh
Comment by Dinesh S Thakur — April 5, 2016 @ 1:16 pm |
Thanks! Does that mean that David Speyer won’t publish an article on that anymore, if Thakur has used his arguments in his paper?
Comment by Timmon Spear — April 10, 2016 @ 2:03 pm |
Ah ok, i thought it’s a two-author paper now. just saw it doesnt give the proof by speyer, but continues working useing that new technique. Is there still work in progress in Speyers paper or is it already submitted?
Comment by Timmon Spear — April 10, 2016 @ 2:09 pm |