Polymath proposal: bounded gaps between primes

June 4, 2013

Polymath proposal: bounded gaps between primes

Filed under: planning,polymath proposals — Terence Tao @ 4:31 am

Two weeks ago, Yitang Zhang announced his result establishing that bounded gaps between primes occur infinitely often, with the explicit upper bound of 70,000,000 given for this gap. Since then there has been a flurry of activity in reducing this bound, with the current record being 4,802,222 (but likely to improve at least by a little bit in the near future).

It seems that this naturally suggests a Polymath project with two interrelated goals:

Further improving the numerical upper bound on gaps between primes; and
Understanding and clarifying Zhang’s argument (and other related literature, e.g. the work of Bombieri, Fouvry, Friedlander, and Iwaniec on variants of the Elliott-Halberstam conjecture).

Part 1 of this project splits off into somewhat independent sub-projects:

Finding narrow ~~prime~~ admissible tuples of a given cardinality (or, dually, finding large ~~prime~~ admissible tuples in a given interval). This part of the project would be relatively elementary in nature, relying on combinatorics, elementary number theory, computer search, and perhaps some clever algorithm design. (Scott Morrison has already been hosting a de facto project of this form at this page, and is happy to continue doing so).
Solving a calculus of variations problem associated with the Goldston-Yildirim-Pintz argument (discussed at this blog post, or in this older survey of Soundararajan) [in particular, this could lead to an improvement of a certain key parameter $k_0$ , currently at 341,640, even without any improvement in the parameter $\varpi$ mentioned in part 3. below.]
Delving through the “hard” part of Zhang’s paper in order to improve the value of a certain key parameter $\varpi$ (which Zhang sets at 1/1168, but is likely to be enlargeable).

Part 2 of this project could be run as an online reading seminar, similar to the online reading seminar of the Furstenberg-Katznelson paper that was part of the Polymath1 project. It would likely focus on the second half of Zhang’s paper and would fit well with part 1.3. I could run this on my blog, and this existing blog post of mine could be used for part 1.2.

As with other polymath projects, it is conceivable that enough results are obtained to justify publishing one or more articles (which, traditionally, we would publish under the D.H.J. Polymath pseudonym). But it is perhaps premature to discuss this possibility at this early stage of the process.

Anyway, I would be interested to gauge the level of interest and likely participation in these projects, together with any suggestions for improving the proposal or other feedback.

Comments (82)

82 Comments »

Sounds fun! I’ll start writing a blog post about simulated annealing of almost-admissible sequences!

Since this proposal is on a ‘current topic’, we should perhaps be careful about people already working in private on these matters. We don’t want the existence of a public project to disincentivize people working in the traditional manner if they choose. I’m not really sure if there’s anything concrete to do in this regard, however.

Comment by Scott Morrison — June 4, 2013 @ 4:39 am | Reply
- But since it is a “very hot current topic,” I would assume that all those working in private are well aware that a lot of people are doing the same. The existence of a polymath project on this won’t make the “problem” any worse.
  
  Comment by François G. Dorais — June 4, 2013 @ 5:06 am | Reply
  - Well, in principle it could cause all blue-eyed analytic number theorists to commit suicide a hundred days from now…
    
    Seriously, though, it may perhaps make some sense to define the scope of the project a bit; I don’t think the project could try to cover every single possible way to develop Zhang’s breakthrough, and there should still be plenty of room for more traditional research in this area. One small precedent here is this preprint of Tim Austin on a new proof of the density Hales-Jewett theorem that benefited from the Polymath1 project on a very closely related topic that was going on at the time, but was still sufficiently different that it could be published separately (in J. Theoret. Prob.). So this is at least an existence proof that Polymath projects and traditional research projects can coexist in the same area. Note also that Pintz has just written an article building on Zhang’s work that is also orthogonal to the current project.
    
    Comment by Terence Tao — June 4, 2013 @ 5:17 am | Reply
    - There is now another Zhang-related paper on the arXiv: http://arxiv.org/abs/1306.0948 So I don’t think that the Polymath8 project is “crowding out” all other Zhang-related research completely. In fact, it may be reducing some duplication of effort, as other researchers in the area will likely choose to focus on the (many) other directions to pursue here than the task of numerical optimisation (which, in many ways, is the direction best suited for a polymath approach), and also may be benefiting from following the Polymath discussions.
      
      Comment by Terence Tao — June 6, 2013 @ 3:34 pm | Reply
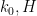      - And now we have the first Zhang-related paper that has seriously overlapped and interacted with our own project: Pintz’s paper http://arxiv.org/abs/1306.1497 which gave for the first time a new value of $\varpi$ (and also values of $k_0, H$ , but Polymath had already passed those by that stage). But thanks to Pintz we were able to improve our own values of 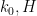$k_0,H$ by a factor of seven or so, and have accelerated our reading program, so it looks like so far there is an at least partly positive relationship between Polymath and traditional research.
        
        Comment by Terence Tao — June 7, 2013 @ 3:04 pm | Reply
Because of this comment “If this sequence has an infinite number of terms in which a(n) = 3, then the twin prime conjecture can be proved.” at http://oeis.org/A165959 I am wondering if there might be interest in seeing what this topic involves with Ramanujan primes?

Comment by John Nicholson — June 4, 2013 @ 5:14 am | Reply
Perhaps a wiki page would be a reasonable place to start for 3. above (tracking down $\varpi$ ). I tried looking through a bit, but there seem to be an awful lot of places where he uses some inequality on $\varpi$ without really saying what it is (because the inequality holds for $\varpi=1/1168$ ).

Comment by Scott Morrison — June 4, 2013 @ 7:01 am | Reply
There seems to be yet another paper on that topic today on the arXiv: http://arxiv.org/abs/1306.0511

Comment by Thomas Sauvaget — June 4, 2013 @ 7:27 am | Reply
I’m certainly interested in 3 (delving into the hard part) as long as the pace is not too much for me. I suspect there is something to be gained from messing around with the decomposition coming from Heath-Brown’s identity. Working out what is optimal here might be a little challenging. Working out the optimal value of $\varpi$ in the rest of the argument as it currently stands (or in any modification of it) should be a routine calculation: I’m not sure whether Zhang actually did this exactly, or whether $\varpi = 1/1168$ was just a convenient value for him. Anyway, that seems to be relatively easily checkable. Beyond that one would be getting to the point of having to find significant new twists on the argument.

Comment by bengreen — June 4, 2013 @ 8:14 am | Reply
- 1/1168 was certainly convenient, not optimal. From my reading, he actually takes the *smallest* $r$ that works in the decomposition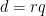 $d=rq$ rather than the largest. Since you win by $\sqrt r$ at that part, you should take $r$ bigger, and then (fingers crossed) the $\omega$ -limitation drops out of Sections 13 and 14, largely leaving it in the decompostion of Sec 6, where you mention H-B can be used. 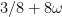I get $\omega<1/320$ from the last display there as $3/8+8\omega<1/2-32\omega$ , but I don't see why exactly there is an "8" in his $3/8+8\omega$ definition of $x_1$ to pass a barrier (32 here is also 4 times that 8). This seems more deeply embedded in the paper somewhere. Given what I have seen so far in Zhang's use of $\omega$ at other junctures, it could well be something like: that 8 is twice 4, where 4 was to beat 3 by epsilon, and 3 was in turn to beat 2 by epsilon, so really 8 could be 4+epsilon, just speculation I don't really know. 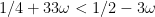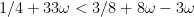There are minor uses of $\omega$ variously appearing, like on pages 43/44 he conveniently wants to merge error bounds, so $1/4+33\omega<1/2-3\omega$ and/or $1/4+33\omega<3/8+8\omega-3\omega$ are used. 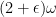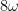Again the " $3\omega$ " here is probably really $(2+\epsilon)\omega$ and the $33\omega$ probably is induced from the $8\omega$ choice somehow.
  
  Comment by v08ltu — June 4, 2013 @ 6:57 pm | Reply
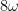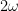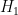  - Why does it not Tex for me? Anyway, on middle page 41 is one place where “8” in $8\omega$ is used. See 11.5 in particular. But the whole thing is loaded, as Zhang wants to win by $2\omega$ here so that he wins by $\omega$ in 11.6 after Cauchy, but as I say, he only needs to win by $\epsilon$ in 11.16 (see 10.15 and above). The “8” here is essentially to beat the “5” in $H_1$ in 10.17 plus “2” from the 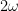$2\omega$ that he takes $d$ past the sqrt-barrier ( 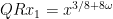$QRx_1=x^{3/8+8\omega}$ , while Lemma 4 is phrased to allow it as low as 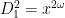$D_1^2=x^{2\omega}$ . NOTE: This “R” and “r” are NOT related to that appearing in 13 and 14 (those sections are independent).
    
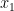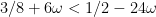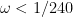    So maybe 6 of the “8” are necessary in $x_1$ , this being thrice the “2” that $d$ exceeds the sqrt-barrier. This then reduces the bound in decomposition from section 6, to $3/8+6\omega<1/2-24\omega$ or $\omega<1/240$ . I would tentatively state this as a "goal" for the lower-fruit $\omega$ -reduction crowd, as I did not see anything much worse if at all (other than 13 and 14 which I perceive has rectification), and to improve it might require a lot more work.
    
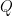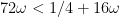    There is also the issue of splitting Type I vs II, as Zhang takes Type I as large as possible (see middle page 40) that still allows to bound "diagonal" terms, but the overlap of where the arguments work could provide a gain. 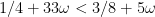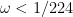One actually has higher powers of $Q$ in Sect 12 (Type II) than 11, so maybe his choice is best, though I think it still has $\omega$ -wiggleroom (in S12 he has $72\omega<1/4+16\omega$ and $1/4+33\omega<3/8+5\omega$ both for $\omega<1/224$ , but as I say I don't trust the constants to be mandatory).
    
    [To use LaTeX in comments, see https://polymathprojects.org/how-to-use-latex-in-comments/ -T]
    
    Comment by v08ltu — June 4, 2013 @ 8:05 pm | Reply
    - Did you type “latex” and a blank after the opening “$”? Example: $8\omega$
      
      Comment by Américo Tavares — June 4, 2013 @ 8:35 pm | Reply
    - Dear v08ltu,
      
      Thanks for the analysis! It may take a while for the rest of us to catch up to you to the point where we can confirm your calculations, but we have just launched the reading seminar for Zhang’s paper at http://terrytao.wordpress.com/2013/06/04/online-reading-seminar-for-zhangs-bounded-gaps-between-primes/ where this discussion is going to take place. 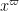As noted in that post, one natural place for optimisation is to decouple the two different uses of the parameter $\varpi$ in Zhang’s argument, both as the upper bound $x^{1/2+2\varpi}$ for the residue class q, and also as the upper bound $x^\varpi$ for the primes dividing that residue class. 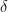In my post, I changed the latter upper bound to $x^\delta$ as the sieve-theoretic step suggests that it can be beneficial to reduce $\delta$ if this helps increase $\varpi$ . 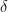So it may be a good idea to go through Zhang’s paper and separate which of the $\varpi$ ‘s in his arguments are actually $\delta$ ‘s.
      
      Comment by Terence Tao — June 4, 2013 @ 8:50 pm | Reply
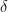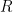      - Admittedly I have not drawn a leitfaden of the paper, but I think the main (maybe only) place your $\delta$ is actually used apart from computations of 4&5 is in Lemma 4. This allows Zhang to specify a range of $r$ in Section 14 though as I say I don’t think it has overriding value there, and also this Lemma rigs 7.4 for the range of $R$ . This latter has various middling import throughout 7-12, but again Zhang has situated its range-ratio as $\omega$ for convenience I find.
        
        Comment by v08ltu — June 4, 2013 @ 10:52 pm | Reply
    - Not sure where to put this, so maybe here with “goals” for $\varpi$ .
      
      In the discussion at Terry’s new analysis obtains a value for $k_0$ from a given value of $\varpi$ which is ‘optimal’, in the sense that one obtains the same values (in the parameter range we’re interested in) as one would get if the parameter $\kappa$ were actually zero.
      
      If you pretend $\kappa$ really is zero, you can simply solve for $k_0$ as a function of $\varpi$ . For the sake of recording that, it’s
      
      $k_0 = \lceil \frac{1+2\varpi + \sqrt{1+4\varpi}}{8 \varpi^2} \rceil.$
      
      Comment by Scott Morrison — June 5, 2013 @ 12:43 am | Reply
      - Thanks Scott!
        
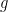        The argument that converts a value of $\varpi$ to a value of $k_0$ actually has as a parameter a certain test function $g: [0,1] \to {\bf R}$ , For convenience, and following Goldston-Pintz.Yildirim, we only consider functions $g$ of a specific form, namely monomials 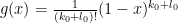$g(x) = \frac{1}{(k_0+l_0)!} (1-x)^{k_0+l_0}$ so that one is only left with a scalar parameter 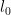$l_0$ to optimise over rather than an infinite-dimensional parameter 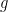$g$ . Once one does that, your formula represents the optimal value of $k_0$ one could extract from a given value of $\varpi$ assuming that $\kappa$ is negligible (which it appears to be in practice). 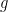But there is some scope to choose more clever functions $g$ that give better results. If you look at the original GPY paper at http://arxiv.org/abs/math/0508185 you will see two tables. 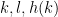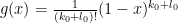Table 1 on page 9 gives the values of $k_0, l_0, H$ (there called $k,l,h(k)$ ) for a given value of $\theta$ (which corresponds in our notation to $1/2 + 2\varpi$ ), using the monomial ansatz $g(x) = \frac{1}{(k_0+l_0)!} (1-x)^{k_0+l_0}$ . 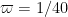Table 2 on page 12 gives the results when one optimises over polynomials of a certain degree rather than monomials, and for instance when $\theta =0.55$ (which corresponds in our notation to $\varpi = 1/40$ ) they get a two-fold improvement in the value of $k_0$ . I don’t know yet how this scales to our value of $\varpi$ but there is certainly some potential for improvement on this score. I guess my blog post at http://terrytao.wordpress.com/2013/06/03/the-prime-tuples-conjecture-sieve-theory-and-the-work-of-goldston-pintz-yildirim-motohashi-pintz-and-zhang/ is the place for further discussion of this direction.
        
        Comment by Terence Tao — June 5, 2013 @ 1:32 am | Reply
[…] work and related questions and results can be found now in Terry Tao’s blog. Terry Tao also proposed a new polymath project aimed to reading Zhang’s paper and attempting to improve the […]

Pingback by Why is mathematics possible? | Combinatorics and more — June 4, 2013 @ 8:55 am | Reply
Emmanuel Kowalski just posted at http://blogs.ethz.ch/kowalski/2013/06/04/bounded-gaps-between-primes-some-grittier-details/ on what would be part 2 of the polymath project, which should be a valuable resource.

I’ve just started a wiki page at http://michaelnielsen.org/polymath1/index.php?title=Bounded_gaps_between_primes to collect a bunch of relevant links for the project. More contributions welcome of course.

Comment by Terence Tao — June 4, 2013 @ 4:35 pm | Reply
- Hi Terry,
  
  thanks for the amazing wiki page! I think it’s a little strange to list all of the improvements to k_0 as being due to me — I did nothing but type in some formulas you derived, and run a bisection search for optimal values of some parameters. Would you object if I edited these to either Tao or Morrison/Tao?
  
  Comment by Scott Morrison — June 4, 2013 @ 11:39 pm | Reply
  - Sure, this is fine with me :)
    
    Comment by Terence Tao — June 5, 2013 @ 1:24 am | Reply
I’m in. I’m especially looking forward to the reading-seminar look at the paper. Gotta love the polymaths –

Comment by mixedmath — June 4, 2013 @ 7:48 pm | Reply
[…] obtained the explicit value of for . A polymath project has been proposed to lower this value and also to improve the understanding of Zhang’s results; as of this time […]

Pingback by Online reading seminar for Zhang’s “bounded gaps between primes” | What's new — June 4, 2013 @ 8:44 pm | Reply
Given the level of interest, I’ve decided to go ahead and “officially” open the Polymath8 project, with the reading seminar being launched at http://terrytao.wordpress.com/2013/06/04/online-reading-seminar-for-zhangs-bounded-gaps-between-primes/ . The post here can be used as the “discussion” thread for all metacomments about the organisation of the project, with the other posts (the reading seminar, the sieve theory post, and Scott’s post on admissible tuples being the “research” threads for the three different aspects of the Polymath project.

Comment by Terence Tao — June 4, 2013 @ 8:47 pm | Reply
I’ve just been pointed towards some online annotation software at http://nb.mit.edu/welcome which might be useful for the reading seminar. I do not have any experience with using these sorts of things, does anyone have any opinion on these sorts of tools? One thing I worry about is that if we use any form of technology more complicated than a blog comment box, we might lose some of the participants who might be turned off by the learning curve required.

Comment by Terence Tao — June 4, 2013 @ 9:57 pm | Reply
- I’m not 100% sure of what your needs are for sharing but the Open Knowledge Foundation has a project meant to do something similar in a blog-post context (or with any piece of text on a web page): http://okfnlabs.org/annotator/
  
  There is a WordPress plugin for it as well: https://github.com/okfn/annotator-wordpress
  
  Comment by tbartels (@tbartels) — June 4, 2013 @ 10:50 pm | Reply
Is there an accessible copy of the Zhang paper, for those of us without access to Annals of Mathematics?

Comment by John — June 5, 2013 @ 3:06 am | Reply
- There’s a dropbox link on this mathoverflow thread if you dig through the comments.
  
  http://mathoverflow.net/questions/131185/philosophy-behind-yitang-zhangs-work-on-the-twin-primes-conjecture/131354#131354
  
  Comment by keepgrabbing.py — June 5, 2013 @ 5:33 am | Reply
  - Thanks, that’s great!
    
    Comment by John — June 7, 2013 @ 7:10 pm | Reply
[…] Polymath proposal: bounded gaps between primes (polymathprojects.org) […]

Pingback by Yitang Zhang latest… | cartesian product — June 5, 2013 @ 9:47 pm | Reply
[…] the meantime, an official polymath8 project has started. The wiki page is a good place to get started. Work to understand and improve the […]

Pingback by More narrow admissible sets | Secret Blogging Seminar — June 6, 2013 @ 3:50 am | Reply
Provided that Tao’s new observation k_0=11018 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 116386 since

1, -1, p(386), -p(386), p(387), -p(387), …, p(5893), -p(5893)

form an admissible set with diameter 116386, where p(n) denotes the n-th prime.

Below is my Mathematica program for checking the admissibility.

rMod[m_,n_]:=Mod[m,n,-n/2]
R[m_,n_]:=R[m,n]=Length[Union[{1,-1},Table[rMod[Prime[m+k],Prime[n]],{k,1,5508}],
Table[rMod[-Prime[m+k],Prime[n]],{k,1,5508}]]]
Do[Do[If[R[m,n]==Prime[n],Goto[aa]],{n,2,m+5508}];
Print[m,” “,OK];Label[aa];Print[m];Continue,{m,385,385}]

Comment by Anonymous — June 7, 2013 @ 1:47 pm | Reply
- Thanks! I’ve added this to the wiki at http://michaelnielsen.org/polymath1/index.php?title=Bounded_gaps_between_primes#World_records . Incidentally the disucssion on improving the diameter given k_0 is ongoing at http://sbseminar.wordpress.com/2013/06/05/more-narrow-admissible-sets ; with the most recent value of 10,719 for k_0, we currently have a value of 108,990 for H; looks like we’re going to get into five digits shortly!
  
  Comment by Terence Tao — June 7, 2013 @ 2:50 pm | Reply
Sorry, I forgot my signature. The last message (concerning the new bound 116386) was posted by me. —-Zhi-Wei Sun (Nanjing Univ., China)

Comment by Anonymous — June 7, 2013 @ 1:49 pm | Reply
[…] bound quickly tumbled much further than that, and Terry Tao initiated a new Polymath project to coordinate efforts. Participants are trying to optimise three […]

Pingback by Bound on prime gaps bound decreasing by leaps and bounds | The Aperiodical — June 8, 2013 @ 1:43 pm | Reply
[…] bound quickly tumbled much further than that, and Terry Tao initiated a new Polymath project to coordinate efforts. Participants are trying to optimise three […]

Pingback by List of Misconceptions and Prime Gap Checkin | Pink Iguana — June 8, 2013 @ 3:00 pm | Reply
[…] bound for the gaps. Here are links for three posts (I, II, III) on Terry Tao’s blog and for a post on the polymath blog. And here is the table for the world records so […]

Pingback by Polymath8: Bounded Gaps Between Primes | Combinatorics and more — June 10, 2013 @ 10:27 pm | Reply
Provided that k_0=5937 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 58866 since

1, -1, p(232), -p(232), p(233), -p(233), …, p(3198), -p(3198), p(3199)

form an admissible set with diameter 58866, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 5:22 am | Reply
Provided that k_0=5459 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53898 since

1, -1, p(228), -p(228), p(229), -p(229), …, p(2955), -p(2955), p(2956)

form an admissible set with diameter 53898, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 6:20 am | Reply
21.Provided that k_0=5454 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53842 since

1, -1, p(228), -p(228), p(229), -p(229), …, p(2953), -p(2953)

form an admissible set with diameter 53842, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 6:32 am | Reply
Provided that k_0=5453 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53824 since

1, -1, p(228), -p(228), p(229), -p(229), …, p(2952), -p(2952), p(2953)

form an admissible set with diameter 53824, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 6:39 am | Reply
Provided that k_0=5453 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53814 since

1, -1, p(236), p(237), … , p(2961), -p(218), -p(219), …, -p(2942)

form an admissible set with diameter 53814, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 7:14 am | Reply
Provided that k_0=5453 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53802 since

1, -1, p(234), p(235), … , p(2959), -p(218), -p(219), …, -p(2942)

form an admissible set with diameter 53802, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 7:28 am | Reply
Provided that k_0=5453 is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53774 since

1, -1, p(232), p(233), … , p(2957), -p(218), -p(219), …, -p(2942)

form an admissible set with diameter 53774, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 19, 2013 @ 7:40 am | Reply
- I have posted the admissible set (in iterm 26) of cardinality k_0=5453 with diameter H=53774 to my homepage with the website
  http://math.nju.edu.cn/~zwsun/admissible_5453_53774.txt
  
  Comment by Anonymous — June 19, 2013 @ 8:27 am | Reply
- I have posted the admissible set (in iterm 26) of cardinality k_0=5453 with diameter H=53774 to my homepage with the website
  http://math.nju.edu.cn/~zwsun/admissible_5453_53774.txt
  
  — Zhi-Wei Sun (Nanjing Univ., China)
  
  Comment by Anonymous — June 19, 2013 @ 8:30 am | Reply
Provided that k_0=5455 (suggested by v08ltu) is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53672 since

1, -1, p(218), -p(218), … , p(2943), -p(2943), p(2944)

form an admissible set with diameter 53672, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

—Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 20, 2013 @ 5:12 am | Reply
Provided that k_0=5452 (suggested by v08ltu) is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53606 since

1, p(218), p(219), …, p(2974), -1, -p(218), -p(219), …, -p(2910)

form an admissible set with diameter 53606, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

Comment by Zhi-Wei Sun — June 20, 2013 @ 5:44 am | Reply
Provided that k_0=5452 (suggested by v08ltu) is correct, I have obtained that Zhang’s bound (Tao’s H) can be improved to 53548 since

1, p(218), p(219), …, p(3196), -1, -p(218), -p(219), …, -p(2688)

form an admissible set with diameter 53548, where p(n) denotes the n-th prime.

It is easy to check the admissibility of this set via Mathematica.

Comment by Zhi-Wei Sun — June 20, 2013 @ 5:56 am | Reply
We have found an admissible set of cardinality k_0=5452 with diameter 51520, which is available from the website
http://math.nju.edu.cn/~zwsun/admissible_5452_51520.txt
Thus, provided that k_0 can be taken as 5452 as suggested by v08ltu, then we improve Zhang’s bound (Tao’s H) to 51520.
It is easy to check the admissibility of this set via Mathematica.

—Qing-Hu Hou (Nankai Univ., China) and Zhi-Wei Sun (Nanjing Univ., China)

Comment by Zhi-Wei Sun — June 20, 2013 @ 6:48 am | Reply
- After comparison we find that our admissible set is a slight variant of Sutherland’s admissible set of cardinality 5453 with diameter 51526.
  
  — Qing-Hu Hou and Zhi-Wei Sun (June 20, 2013)
  
  Comment by Anonymous — June 20, 2013 @ 7:36 am | Reply
[…] a la conjetura de los números primos gemelos, y por otra, todo el revuelo que había generado en polymath encabezado por el mismísimo Tao a la […]

Pingback by El avance de la ciencia hoy en día y como contribuir. | Adsu's Blog — June 25, 2013 @ 6:43 am | Reply
For any integer k>1, define H(k) as the least possible diameter of an admissible set of k distinct integers. I conjecture that H(k)>k*H_k for all k>4, where H_k denotes the harmonic number 1+1/2+…+1/k. This conjecture can be further strengthened, for example, H(k)>k*H_{k+2} for all k>6.

— Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 28, 2013 @ 3:35 pm | Reply
In addition to item 32, I also conjecture that H(k) 1.

— Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 28, 2013 @ 3:54 pm | Reply
- I don’t know why the formula cannot appear correctly. I mean that I also conjecture that H(k) with k>1 is smaller than k*(1+1/2+1/3+…+1/(2k)).
  
  –Zhi-Wei Sun (Nanjing University, China)
  
  Comment by Zhi-Wei Sun — June 28, 2013 @ 3:57 pm | Reply
Moreover, I conjecture that H(k)/k – log(k) has a finite limit s>0. It seems that s lies in the interval (0.6,0.8).

— Zhi-Wei Sun (Nanjing Univ., China)

Comment by Zhi-Wei Sun — June 28, 2013 @ 4:43 pm | Reply
After certain computation, here I propose a new reasonable conjecture to replace the one stated in item 34.

CONJECTURE. For any integer k>1, define H(k) as the least possible diameter of an admissible set of k distinct integers, and let H_k be the harmonic number 1+1/2+…+1/k. Then

H(k) / k = H_k +O(1/(log k)) as k tends to the infinity.

— Zhi-Wei Sun (Nanjing Univ., China)

Comment by Zhi-Wei Sun — June 28, 2013 @ 5:46 pm | Reply
Here I state my formal conjecture on admissible sets (in final form).

CONJECTURE (June 28, 2013). For any integer k>1, define H(k) as the least possible diameter of an admissible set of k distinct integers, and let H_k be the harmonic number 1+1/2+…+1/k. Then
we have 0 < H(k) / k – H_k 4, where gamma denotes to the Euler constant 0.5772…

I have verified this conjecture for k up to 5000. See also my comments available from http://oeis.org/A008407 .

— Zhi-Wei Sun (Nanjing University, China)

Comment by Anonymous — June 29, 2013 @ 2:14 am | Reply
- As the formula in iterm 36 did not appear correctly (due to htm problem), “we have 0 < H(k) / k – H_k 4" should be " H(k) / k – H_k is positive and smaller than (gamma+2) / (log k). "
  
  Comment by Zhi-Wei Sun — June 29, 2013 @ 2:23 am | Reply
Here I propose a new Goldbach-type conjecture concerning minimal diameters of admissible sets.

CONJECTURE (June 30, 2013). For any integer k>1 let H(k) be the least possible diameter of an admissible set of k distinct integers. Then, every n=5,6,… can be written in the form H(j) + H(k)/2, where j and k are integers greater than one.

For example, 25 = T(5)+T(8)/2 = 12 + 26/2. For numbers of such representations, the reader may visit http://oeis.org/A227083 .

— Zhi-Wei Sun (Nanjing University, China)

Comment by Zhi-Wei Sun — June 30, 2013 @ 6:41 pm | Reply
- In the example, T(5) and T(8) should be H(5) and H(8) respectively. By the way, the reader may visit http://oeis.org/A008407 to see my other conjectures involving H(k).
  
  Comment by Zhi-Wei Sun — June 30, 2013 @ 6:45 pm | Reply
Here I pose a new conjecture concerning minimal diameters of admissible sets.

CONJECTURE (July 2, 2013). For any integer k>1 let H(k) be the least possible diameter of an admissible set of k distinct integers. Then, every positive integer different from 23 can be written in the form x^2 + H(k)/2, where x and k>1 are integers.

For example, 378 = 64 + 314 = 8^2 + H(110)/2. For numbers of such representations, the reader may visit http://oeis.org/A227156 .

Comment by Zhi-Wei Sun — July 3, 2013 @ 4:16 am | Reply
What happened on July 3rd, 2012

In his work on the twin prime numbers, people all read that he had a breakthrough on July 3, 2012. The big idea he got on July 3 last year was that he realized that the problem could be reduced to several cases. He felt that he could handle them, especially one case was simple to be proved. But he was not completely right. The simplest case turned out to the most complicated. This is the place where the Weil conjecture was used. But he quickly learned the relevant theories and patched up the arguments. He is very happy with this.

http://blog.sina.com.cn/s/blog_c24597bf0101cf89.html

Comment by z — July 19, 2013 @ 7:15 pm | Reply
maybe some new tips for this problem. My research area is symbolic dynamics theory. I find primes gap pattern may be described by the chaos orbit of Logistic mapping X(k+1)=1-uX(k)^2, u=1.5437. A very preliminary work could be found at http://arxiv.org/abs/1306.3626. wish it’s useful :)

Comment by Wang Liang — July 20, 2013 @ 7:29 am | Reply
[…] main objectives of the polymath8 project, initiated back in June, were “to understand the recent breakthrough paper of Yitang Zhang establishing an infinite […]

Pingback by Polymath8 – A Success ! | The polymath blog — September 20, 2013 @ 7:09 pm | Reply
[…] 6. Polymath proposal: bounded gaps between primes | The polymath blog […]

Pingback by zhang twin prime breakthru vs academic track/grind | Turing Machine — October 4, 2013 @ 9:53 pm | Reply
[…] most recent polymath success – improving the bound between gaps of primes from 70,000,000 to 4,680 – has me […]

Pingback by Is neuroscience mature enough for a #polybrain project to exist? | neuroecology — November 21, 2013 @ 3:57 pm | Reply
[…] Los Angeles, a winner of the Fields Medal, mathematics’ highest honor, had created a “Polymath project,” an open, online collaboration to improve the bound that attracted dozens of […]

Pingback by NFTF » Sudden Progress on Prime Number Problem Has Mathematicians Buzzing — November 22, 2013 @ 12:47 pm | Reply
Take any twin prime (n,m). n mod 3 = 2 , m mod 3 = 1. The first prime number of the pair will always be 2 and the second prime will always be 1.

Comment by Luiz Roberto Meier — November 23, 2013 @ 12:33 pm | Reply
[…] Los Angeles, a winner of the Fields Medal, mathematics’ highest honor, had created a “Polymath project,” an open, online collaboration to improve the bound that attracted dozens of […]

Pingback by Sudden Progress on Prime Number Problem Has Mathematicians Buzzing | Learn How to be Prepared — November 23, 2013 @ 8:43 pm | Reply
[…] Los Angeles, a winner of the Fields Medal, mathematics’ highest honor, had created a “Polymath project,” an open, online collaboration to improve the bound that attracted dozens of […]

Pingback by Crowd-sourcing shrinking the prime gap | Later On — November 30, 2013 @ 6:54 pm | Reply
I thought of this when I thought of the problem, I go into more detail in the link I provide. But first you can prove that a number is the second of a pair of twin primes if and only if it divides no prime up to the square root of the number with a remainder of 2 or 0. Then I use this estimate for the number of pairs of twin primes: up to N=(p+1)^2-1 for a prime p. N*(1/2)*(3/5)*(5/7)*…*(p-2)/p, this follows from the statistical notion that of all the numbers up to N, (3/5) for example will not divide 5 by 0 or 2. so (p-2)/p is the fraction of numbers up to N that does not divide p with a remainder of 0 or 2 and these are multiplied for every prime up to the square root of N to give an estimate of the number of pairs of twin primes less than N. Then I show that this estimate tends towards infinity with increasing N, thus I conclude that there are an infinite number of twin primes. Maybe someone could explain why this doesn’t work?
http://benpaulthurstonblog.blogspot.com/2013/11/even-simpler-idea-for-proof-of-twin.html

Comment by Ben Thurston — December 4, 2013 @ 10:19 am | Reply
[…] as we move along the number line. A bunch of mathematicians including Terrance tao worked further (polymath project on this) and improved that gap to as a few thousands. The latest result from Maynard brings in an […]

Pingback by The new Prime gap | On the learning curve... — December 4, 2013 @ 12:13 pm | Reply
[…] améliorations des arguments de Y. Zhang. Le 4 juin, T. Tao a créé dans le cadre du « projet Polymath », une collaboration ouverte et en ligne qui a attiré des dizaines de mathématiciens. Le […]

Pingback by Conjecture des nombres premiers jumeaux : l'étau se resserre | Sciences-Campus Info — December 15, 2013 @ 3:45 pm | Reply
[…] Tao с группой коллег организовал коллективный проект polymath8a, целью которого было снижение доказанной верхней […]

Pingback by Коллективный разум в теории простых чисел « Домик Миа — February 23, 2014 @ 4:21 pm | Reply
j’ai trouvé une démonstration de la Conjecture des nombres premiers jumeaux. il consiste a ….. contact moi cyber_hmza@hotmail.fr

Comment by sadaoui hamza — March 15, 2014 @ 8:07 pm | Reply
. I began to wonder if more columns of elimination like 5 and the even numbers could be found.

I started off by finding the possible prime numbers by making a row consisting of a series of numbers derived from multiples of 6 + or- 1. I also wanted the “5” column to line up. So, by multiplying 5 by 6 (30) I was able to determine where my rows would begin. I started the first column with the prime number,5 and then added 30 to each row to determine where next row on possible prime numbers would start. This created the column of elimination I was looking for.

The square of prime numbers that do not fall within the first column follow in a sequence of 6: 5, 11, 17, and 23. These create addition columns of Elimination.

5 6 7 11 12 13 17 18 19 23 24 25 29 30 31
35 36 37 41 42 43 47 48 49 53 54 55 59 60 61
65 66 67 71 72 73 77 78 79 83 84 85 89 90 91
95 96 97 103 104 105 107 108 109 113 114 115 119 120 121
125 126 127 133 134 135 137 138 139 143 144 145 149 150 151

I would follow this process for each following prime number.
7 x 6: 42 added to each row
7 11 13 17 19 23 29 31 37 43 47
49 53 59 61 67 71 73 77 79 83 89
91 97 103 107 109 113 115 119 121 127 131
133 137 143 149 151

11 x 6: 66 added to each row
11 13 17 19 23 29 31 37 43 47 49 53 59 61 67 71 73
77 79 83 89 97 103 107 109 113 115 119 121 127 131 137 139
143 149 151 187
253
13 x 6: 78 added to each row
13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 79 83 89
91 97 103 107 109 113 115 119 121 127 131 137 139 149 151
169

17 x 6: 102
17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 79 83 89
119 127 131 137 139 149 151
221 287
398

Comment by Mr. Spud Getty — December 4, 2018 @ 1:10 pm | Reply
[…] Благодаря последовавшему за этим открытому проекту Polymath нам известно, что существует бесконечное количество […]

Pingback by [Перевод] Там, где сходятся доказательства, факты и воображение — iT ОБОЗРЕВАТЕЛЬ — April 15, 2019 @ 12:36 pm | Reply
[…] Благодаря последовавшему за этим открытому проекту Polymath нам известно, что существует бесконечное количество […]

Pingback by [Перевод] Там, где сходятся доказательства, факты и воображение – CHEPA website — April 15, 2019 @ 1:03 pm | Reply
[…] della Fields Medal nel 2006 (equivalente del Nobel nel campo della matematica), diede il via al Progetto Polymath, una collaborazione online e aperta per diminuire sempre più il limite. Con ottimi […]

Pingback by I numeri primi non sono poi così soli - Galileo — June 24, 2019 @ 4:29 pm | Reply
[…] Professor Maynard joined Professor Tao’s collaborative polymath project, and the gap was down to 246, were progress has since […]

Pingback by Where do ideas come from? A mathematician ponders eureka moments and solving complex problems – Science News – Australia News and Jobs — August 28, 2019 @ 1:43 pm | Reply
Can anyone contribute to bounded gaps between primes project? I have some ideas, not in Zhang’s line though. I’m a physicist but have an interest in number theory. How can I share my calculation?

Comment by Monologist — November 17, 2019 @ 9:47 pm | Reply
Here I prove the twin prime conjecture. Please give feedback if I’m right or wrong
https://www.researchgate.net/publication/337468915_A_Simple_Proof_of_Twin_Prime_Conjecture

Comment by Monologist — November 23, 2019 @ 12:29 pm | Reply

RSS feed for comments on this post. TrackBack URI

	Anonymous on Rota’s Basis Conjecture:…
	Cherrypick India on Polymath projects 2021
	tanner808 on Polymath projects 2021
	Anonymous on Polymath 11 is Now Open
	Chenxiao Tian on Polymath 11 is Now Open
	ryeguy10 on Polymath 11 is Now Open
	ndnnnd on Polymath projects 2021
	Prime time on Two polymath (of a sort) propo…
	What comes after exp… on Minipolymath2 project: IMO 201…
	Will AI Replace Math… on Spontaneous Polymath 14…
	gui7575 on A new polymath proposal (relat…
	Thomas Vu on Polymath projects 2021
	Mary Megrant on Polymath projects 2021
	h0sane on A sort of Polymath on a famous…
	Thomas Vu on Polymath projects 2021

The polymath blog

June 4, 2013