Let us have a little discussion about it.
We may also discuss both general and specific open research mathematical projects which are of different flavor/rules.
Proposals for polymath projects appeared on this blog, in this post on Gowers’s blog, and in several other places.
RSS feed for comments on this post. TrackBack URI
 | Anonymous on Polymath10 is now open |
| Anonymous on Draft version of polymath4… |
| Anonymous on Rota’s Basis Conjecture:… |
| Anonymous on Rota’s Basis Conjecture:… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Non-transitive Dice over Gower… |
| Anonymous on Two polymath (of a sort) propo… |
| Anonymous on Two polymath (of a sort) propo… |
Polymath Wiki – most recent changes
The polymath blog 
Here is a bit of data on the Theme One Program that I worked on all through the 1980s. The aim was to develop fundamental algorithms and data structures to support an integrated learning and reasoning interface. I wrote up a pilot version of the program well enough to get a Master’s degree out of it, but still haven’t gotten around to writing up the complete documentation. Below are some links to what I’ve put on the web so far.
• Theme One Program
Comment by Jon Awbrey — February 14, 2013 @ 6:04 pm |
In a way, I see this project as being related to Tim Gowers’ Proposal on the Mathematics of the Origin of Life, since one of my reasons for doing this work was to get what information I could about the threshold of systems-theoretic complexity necessary to support a capacity for inquiry.
More discussion to follow as I get time, either here or on my blog …
Comment by Jon Awbrey — February 14, 2013 @ 10:30 pm |
Thank you, Jon, for your suggestion.
Comment by Gil Kalai — February 15, 2013 @ 2:53 pm |
[…] Re: Next Polymath Project • What, When, Where? […]
Pingback by Theme One • A Program Of Inquiry : 4 | Inquiry Into Inquiry — February 14, 2013 @ 8:50 pm |
For some time I’ve wondered if locking a few knot theorists and model theorists in a room together would be productive. These questions seem like they would be within reach of low-budget techniques, but as far as I can tell they haven’t been addressed (except in a couple of MathOverflow questions from, um, me):
1) Is there a bog-standard metamathematics of skein relations? The Reidemeister moves kind of look like they are playing the role of axioms in a theory. Is there a way to make this honest? E.g., can we integrate skein relations from knot theory into a first-order logical language, so that the Reidemeister moves become the axioms for models of a first-order theory of ambient isotopy, where
* “strands” are the elements of the structures;
* knots and links are the models;
* linking plays the role of logical embedding?
2) if 1 can be carried out, there should be a Fraisse limit of links. Fraisse limits are universal for embedding finitely-generated first-order structures. But any 1-d curve is already homeomorphic to a subset of the Menger sponge. Is the Menger sponge exactly the Fraisse limit of links in the language of skein relations?
Attacking a concrete, solid conjecture has been a pretty successful model for Polymath so far. This idea doesn’t quite fit into that mold, since explicitly phrasing the question in a mathematically meaningful way is part of the work.
Comment by Scott McKuen — February 15, 2013 @ 5:07 pm |
I’m not sure how this is supposed to work, so I’ll just free associate a little and look for intersecting spheres.
I know many people have looked into connections between knot theory and logic. Lou Kauffman comes to mind. Lou makes use of ideas about loopy logic going back to George Spencer Brown, who makes use of ideas about logical graphs going back to Charles Sanders Peirce.
I don’t have much insight into the knotty side of this, but I have explored the less involved logical graphs that work for plain old boolean functions, using a species of cactus graphs to represent propositional formulas and implementing them as graph-theoretic data structures in the computer. This is what I used in the project I linked above.
Comment by Jon Awbrey — February 16, 2013 @ 3:25 pm |
Thanks, Scott, for your suggestion. I suppose the relevant MO question you refer to is http://mathoverflow.net/questions/87002/what-is-the-metamathematical-interpretation-of-knot-diagrams .
Comment by Gil Kalai — February 17, 2013 @ 4:06 pm |
Yes, and also this for part 2: http://mathoverflow.net/questions/53839/what-is-known-about-links-with-a-countably-infinite-number-of-tame-components, which has some points by Bill Thurston and Sergei Melikhov that kill the easiest version of this idea – I don’t know what, if anything, is salvageable.
Comment by Scott McKuen — February 17, 2013 @ 8:37 pm |
Thank you for your proposal to discuss open research projects of different flavors.
I started one such project under working name “Math Research Trends Wiki”: http://researchtrends.wikia.com/ with the motto “research in the middle”.
This my project is now in a rudimentary stage of development but is promising to grow in a big useful scientific endeavor.
The biggest problem with this project right now is that the site which hosts it (Wikia.com) has a trouble with displaying math formulas because it uses an old MediaWiki version, see for example red error messages on this page: http://researchtrends.wikia.com/wiki/Multifuncoid_has_atomic_arguments
I don’t want to host this project myself (without Wikia.com) for two reasons: 1. it would be expensive to pay for a Web hosting for me a poor person; 2. Wikia seems to have better default settings for a site and to reach the same degree of usability I would need to do much configuration and installation myself, what I don’t want to do.
Nevertheless, if somebody may give away his hosting account for this project, I may consider to move to an other hosting.
As I’ve already said this project is rudimentary and it may be not yet clear for others (excluding me, or even including me) what it should grow to.
I am going to post there an example network of related problems (about a specific class of problems in my current research of objects which I call “multifuncoids” and “staroids”) as soon as math formulas will work. Note that I’ve asked Wikia to upgrade their software or at least to say when they are going to upgrade but received no response.
Comment by porton — February 18, 2013 @ 6:49 pm |
Thank you, Porton, for your suggestion.
Comment by Gil Kalai — February 19, 2013 @ 12:57 pm |
[…] at the Polymath blog, Gil Kalai recently proposed a discussion about possible future Polymath projects. This post is partly to direct you to that discussion in […]
Pingback by Whither Polymath? | Gowers's Weblog — February 28, 2013 @ 1:19 pm |
Well, as long as no one else has anything to suggest right at the moment, I might as well indulge in some Meta-Poly-Mathic observations that have occurred to me in this connection.
I have noticed over the years — especially in light of how my own inclinations have shifted — a wide distribution of perspectives toward problem-solving, ranging from those that keep a tight focus on particular problems to those that aim to develop the resource environments, social and technological, in which we try to solve more general classes of problems.
Speaking just from my current point of view, I think it might further the long-terms aims of the project to address the environmental questions a little more directly.
Comment by Jon Awbrey — February 28, 2013 @ 9:16 pm |
There are a few problems that seem like they might admit an elementary, mathcrowd-sourceable solution, or that builds off of other work in a relatively approachable way. Or perhaps they’re easily stated but impossible. It’s hard to say. Nonetheless, I’d like to share them.
In particular, I think the Erdos-Strauss Conjecture, which essentially says that the integer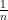
can be written as a sum of three Egyptian fractions; Martin Gardner’s question about whether or not there exists a Magic Square, each of whose entries is a square; and a conjectured extension of the paper [S. A. Burr, “On Moduli for Which the Fibonacci Sequence Contains a Complete System of Residue”, Fibonacci Quarterly, December 1971, pp. 497-504] stating that the sequence 
, where $L(n)$ are the Lucas numbers, contains a complete residue system modulo $m$ if and only if $m$ is one of the following: $2, 4, 6, 7, 14, 3^k, k \geq 1$.
Do any of these seem interesting and/or approachable and/or appropriate? I understand that I have a certain love for number theory – I accept that.
Comment by mixedmath — March 19, 2013 @ 10:45 am |
I always manage to forget to do the things wordpress requires for math to be displayed properly, even if I remembered halfway through.
Comment by mixedmath — March 19, 2013 @ 10:46 am |
Consider also this (informal) problem: We should define “math” in such a way that arbitrary inventions of men (for example, chess game) are not to be considered math, but math is only such things which are related by numerous links with the rest of mathematics. Could we define a numeric measure characterizing how much a specific setting is math? For example, this measure would be low for chess but high for group theory. No idea how to formulate this exactly, but get my rough idea.
Comment by porton — March 19, 2013 @ 11:11 am |
I received permission from PlanetMath staff to post there incomplete research proofs (marked as “Research” major section). I posted there some preliminary materials related with my research: http://planetmath.org/backgroundofseveralopenproblemsistumbledupon – the most important of these is this conjecture: http://planetmath.org/crosscompositionproductofanindexedfamilyoffuncoidsisapointfreefuncoid
Please participate in my research together with me.
I also suggest you to post more research topics at PlanetMath.
I’ve abandoned my project http://researchtrends.wikia.com because we can do it on PlanetMath instead.
Please post more your research projects on PlanetMath.
Comment by porton — March 23, 2013 @ 1:26 pm |
some new ideas on P vs NP. am recently thinking it can be reduced to a particular counting problem that has a basic structure similar to razborov approximation proof(s). would like to engage in dialogue with experts in monotone circuit theory or extremal combinatorics. & also think that stackexchange chat would be an interesting new venue that hasnt been tried or fully exercised yet. anyone interested plz reply on my blog.
Comment by vznvzn — March 31, 2013 @ 4:57 pm |
Sveitsiss? 12:00 paikallista aikaa, UEFA Champions League ja Europa League v?lieriin tasapeliin UEFA p??majassa Nyonissa Sveitsiss? seremoniassa. Kaksi La Liga ja kaksi Bundesliigan joukkueet joutua sis?llissotaan. Barcelona pumpataan Bayern, Real Madrid Zaiyu lohkovaiheessa kilpailijat Dortmund.
Mestarien liigan v?lieriin erityisi? ??nestyksell? tulokset Pelipaidat Suomi ovat seuraavat (lueteltu entinen ensimm?inen osuma koti):
Bayern Munchen vs Barcelona
Dortmund vs Real Madrid
UEFAn p??sihteeri Jos Tarantino FC barcelona pelipaidat puheenjohtajana lippu??nestys, ura pahoillani Ruud van Nistelrooy j?i Mestarien liigan pokaalin vieraana.V?lier?ss? piirt?? on kauden alkua lis?t? linkin.Lippu??nestys ottaa sattumanvaraisesti, ei kylvet??n, ei v?ltt?? saman liigan joukkue.
La Liga (Barcelona ja Real Madrid) ja Bundesliigan (Bayern ja Dortmund) paloitella v?lieriss?. Real Madrid enn?tys 24 osaksi Top 4 voittava numero on juuri summa kolme muuta joukkuetta voittaa numero.
Bundesliigan ensimm?ist? kertaa kaksi joukkuetta Jalkapallo Pelipaidat sai nelj? vahvaa kotona viime kaudella Bayern menetti mestaruuden eliminoidaan lohkovaiheessa Valencia. Dortmund on vain ly?m?t?n t?ll? kaudella finalistit v?lieriin ensimm?ist? kertaa 15 vuoteen, oli jo tavannut kaksi kertaa La Liga joukkue lohkovaiheessa voittaa Real Madrid voitti etunimi, 1/4 finaalissa trilleri pois Malaga.
V?lieriin kaksi kierrosta huhtikuun 23/24 ja 30. huhtikuuta / 1. toukokuuta j?rjestet??n lopullinen Keski-Euroopan aikaa klo 20:45 25. toukokuuta Wembley Stadium Lontoossa.
Comment by barcelonapt3 — April 14, 2013 @ 2:24 am |
some new thinking/results/algorithms on the collatz conjecture based on FSM transducers (new code not yet on that page as of this moment). found a remarkable, apparently breakthrough enumeration/induction/near-fractal pattern yesterday, eager to share/chat about it with any driven experts or amateurs.
Comment by vznvzn — May 24, 2013 @ 4:42 pm |
[…] at the Polymath blog, Gil Kalai recently proposed a discussion about possible future Polymath projects. This post is partly to direct you to that discussion in […]
Pingback by Whither Polymath? | Studywell — June 2, 2013 @ 6:13 pm |