Polymath7 research thread 5: the hot spots conjecture

August 9, 2013

Polymath7 research thread 5: the hot spots conjecture

Filed under: hot spots,research — Terence Tao @ 7:22 pm
Tags: Polymath7

This post is the new research thread for the Polymath7 project to solve the hot spots conjecture for acute-angled triangles, superseding the previous thread; this project had experienced a period of low activity for many months, but has recently picked up again, due both to renewed discussion of the numerical approach to the problem, and also some theoretical advances due to Miyamoto and Siudeja.

On the numerical side, we have decided to focus first on the problem of obtaining validated upper and lower bounds for the second Neumann eigenvalue ${\mu_2}$ of a triangle ${\Omega=ABC}$ . Good upper bounds are relatively easy to obtain, simply by computing the Rayleigh quotient of numerically obtained approximate eigenfunctions, but lower bounds are trickier. This paper of Liu and Oshii has some promising approaches.

After we get good bounds on the eigenvalue, the next step is to get good control on the eigenfunction; some approaches are summarised in this note of Lior Silberman, mainly based on gluing together exact solutions to the eigenfunction equation in various sectors or disks. Some recent papers of Kwasnicki-Kulczycki, Melenk-Babuska, and Driscoll employ similar methods and may be worth studying further. However, in view of the theoretical advances, the precise control on the eigenfunction that we need may be different from what we had previously been contemplating.

These two papers of Miyamoto introduced a promising new method to theoretically control the behaviour of the second Neumann eigenfunction ${u_2}$ , by taking linear combinations of that eigenfunction with other, more explicit, solutions to the eigenfunction equation ${\Delta u = - \mu_2 u}$ , restricting that combination to nodal domains, and then computing the Dirichlet energy on each domain. Among other things, these methods can be used to exclude critical points occurring anywhere in the interior or on the edges of the triangle except for those points that are close to one of the vertices; and in this recent preprint of Siudeja, two further partial results on the hot spots conjecture are obtained by a variant of the method:

The hot spots conjecture is established unconditionally for any acute-angled triangle which has one angle less than or equal to ${\pi/6}$ (actually a slightly larger region than this is obtained). In particular, the case of very narrow triangles have been resolved (the dark green region in the area below).
The hot spots conjecture is also established for any acute-angled triangle with the property that the second eigenfunction ${u_2}$ has no critical points on two of the three edges (excluding vertices).

So if we can develop more techniques to rule out critical points occuring on edges (i.e. to keep eigenfunctions monotone on the edges on which they change sign), we may be able to establish the hot spots conjecture for a further range of triangles. In particular, some hybrid of the Miyamoto method and the numerical techniques we are beginning to discuss may be a promising approach to fully resolve the conjecture. (For instance, the Miyamoto method relies on upper bounds on ${\mu_2}$ , and these can be obtained numerically.)

The arguments of Miyamoto also allow one to rule out critical points occuring for most of the interior points of a given triangle; it is only the points that are very close to one of the three vertices which we cannot yet rule out by Miyamoto’s methods. (But perhaps they can be ruled out by the numerical methods we are also developing, thus giving a hybrid solution to the conjecture.)

Below the fold I’ll describe some of the theoretical tools used in the above arguments.

Let ${\Omega}$ be an acute-angled triangle that is not equilateral, and let ${\mu_2}$ be the second Neumann eigenvalue; as discussed in previous posts, we know that this eigenvalue is simple. The method of Miyamoto allows one to control the structure of the second eigenfunction ${u_2}$ through an analysis of the quadratic form

$\displaystyle {\mathcal H}_{\mu_2}[u] := \int_\Omega |\nabla u|^2 - \mu_2 |u|^2$

for ${u \in H^1(\Omega)}$ (we restrict attention here to real-valued functions). From the spectral theorem, we know that this quadratic form is non-negative when ${u}$ has mean zero, with equality if and only if ${u}$ is a multiple of ${u_2}$ . This leads to the following consequence:

Lemma 1 Let ${v_1,\ldots,v_k \in H^1(\Omega)}$ have disjoint supports. Then ${{\mathcal H}_{\mu_2}[v_i]}$ is non-negative for all but at most one of the ${v_1,\ldots,v_k}$ . If ${k \geq 3}$ and none of the ${v_1,\ldots,v_k}$ vanish identically, we may upgrade “non-negative” in the previous assertion to “strictly positive”.

\bein{proof} Suppose for contradiction that ${{\mathcal H}_{\mu_2}[v_i]}$ and ${{\mathcal H}_{\mu_2}[v_j]}$ are negative for some distinct ${i,j}$ . If we take ${u}$ to be a linear non-trivial combination of ${v_1,v_2}$ which has mean zero, then we see from the disjoint supports of ${v_i,v_j}$ that ${{\mathcal H}_{\mu_2}[u]}$ is also negative, contradicting the non-negativity of ${{\mathcal H}_{\mu_2}}$ on mean-zero functions.

Now suppose that ${{\mathcal H}_{\mu_2}[v_i]}$ and ${{\mathcal H}_{\mu_2}[v_j]}$ are merely non-positive instead of non-negative. Then the above argument shows that there is a non-trivial linear combination of ${v_i,v_j}$ that is a non-zero multiple of ${u_2}$ . On the other hand, if ${k \geq 3}$ and none of the ${v_1,\ldots,v_k}$ vanishing identically, then this linear combination of ${v_i,v_j}$ will be zero on a set of positive measure, which is impossible for a non-zero multiple of the eigenfunction ${u_2}$ (which is real analytic). $\Box$

We have a further non-negativity property of ${{\mathcal H}_{\mu_2}}$ :

Lemma 2 Let ${u \in H^1(\Omega)}$ vanish on two of the three sides of ${\Omega}$ . Then ${{\mathcal H}_{\mu_2}[u] \geq 0}$ , with equality occuring if only if ${u}$ solves the eigenfunction equation ${\Delta u = - \mu_2 u}$ and obeys Neumann conditions on the remaining side of ${\Omega}$ .

Proof: Write ${\Omega =ABC}$ . If ${u}$ vanishes on ${AB}$ and ${BC}$ with ${{\mathcal H}_{\mu_2}[u] < 0}$ , we reflect ${u}$ across ${AC}$ and obtain a function ${\tilde u \in H^1(\tilde \Omega)}$ on the kite ${ABCB'}$ formed by reflecting ${ABC}$ across ${AC}$ , with

$\displaystyle \int_{ABCB'} |\nabla \tilde u|^2 < \mu_2 \int_{ABCB'} |\tilde u|^2$

and so the first Dirichlet eigenvalue ${\lambda_1(ABCB')}$ of ${ABCB'}$ is less than ${\mu_2}$ . But by a result of Friedlander, the first Dirichlet eigenvalue of the convex planar domain ${ABCB'}$ is at least as large as the third Neumann eigenvalue ${\mu_3(ABCB')}$ of that domain. Hence, the symmetric reflection of ${u_2}$ across ${AC}$ cannot be the second or third Neumann eigenfunction for ${ABCB'}$ , and so these functions must both be anti-symmetric instead of symmetric across ${AC}$ . But at least one of these anti-symmetric eigenfunctions must change sign on ${ABC}$ (as they are orthogonal to each other), and will then have at least four nodal domains, contradicting the Courant nodal line theorem. The second claim of the lemma follows by similar arguments and is omitted. $\Box$

This lemma turns out to be particularly useful when applied to the nodal components of a solution to the eigenfunction equation ${\Delta u = - \mu_2 u}$ :

Corollary 3 Let ${u \in H^3(\Omega)}$ be a solution to the eigenfunction equation ${\Delta u = - \mu_2 u}$ , not necessarily obeying the Neumann boundary condition. Let ${\Omega_1,\ldots,\Omega_k}$ be the nodal domains of ${u}$ (i.e. the connected components of ${\{ u \neq 0 \}}$ in ${\Omega}$ ). Then

$\displaystyle \int_{\partial \Omega_i \cap \partial \Omega} u \partial_n u \geq 0 \ \ \ \ \ (1)$

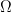
for all but at most one ${i=1,\ldots,k}$ , where ${\partial_n}$ is the derivative in the outward normal direction. If ${k \geq 3}$ , then we can make the inequality (1) strict. Finally, (1) holds (with strict inequality) whenever ${\partial \Omega_i \cap \partial \Omega}$ is contained in one of the three sides of ${\Omega}$

Proof: We apply the previous lemmas with ${v_i := u 1_{\Omega_i}}$ , and observe from integration by parts that

$\displaystyle {\mathcal H}_{\mu_2}[v_i] = \int_{\partial \Omega_i \cap \partial \Omega} u \partial_n u.$

$\Box$

As worked out in previous polymath7 threads, applying this corollary to the Neumann eigenfunction ${u_2}$ yields that the nodal curve is simple and connects two distinct sides of the triangle ${\Omega}$ . However, the new advances of Miyamoto and Siudeja have come from applying this corollary to other solutions to the eigenfunction equation. For instance:

Corollary 4 Let ${u \in H^3(\Omega)}$ be a non-trivial solution to the eigenfunction equation ${\Delta u = - \mu_2 u}$ , not necessarily obeying the Neumann boundary condition. Then the nodal curve ${\{u=0\}}$ does not contain any loops.

This leads to a variant of the maximum principle:

Corollary 5 Let ${u \in H^3(\Omega)}$ be a solution to the eigenfunction equation ${\Delta u = - \mu_2 u}$ , not necessarily obeying the Neumann boundary condition. If ${u \geq 0}$ on ${\partial \Omega}$ , then ${u \geq 0}$ on ${\Omega}$ .

One particularly nice solution ${u}$ to use in the above corollary is a directional derivative of ${u_2}$ , yielding the following result of Siudeja:

Corollary 6 Suppose that ${u_2}$ has no critical points on the interior of two of the three sides of the triangle ${\Omega}$ . Then ${u_2}$ has no critical points in the interior of ${\Omega}$ either. In particular, the hot spots conjecture is true for this triangle.

Proof: Apply the previous corollary to the derivative of ${u_2}$ in the direction normal to the third side, to conclude that that derivative does not change sign in the interior of the triangle. But this is incompatible with a critical point in the interior (as can be seen for instance by a Bessel expansion around that point). $\Box$

Another fruitful solution ${u}$ to use is some linear combination of ${u_2}$ and another solution ${v}$ designed to create a degenerate critical point ${u(p)=\nabla u(p)=0}$ . This gives the following criterion of Miyamoto for excluding critical points at certain locations:

Corollary 7 Let ${p}$ be an interior point of ${\Omega}$ , and let ${v \in H^3(\Omega)}$ be a solution to the eigenfunction equation ${\Delta v = -\mu_2 v}$ with ${v(p)>0}$ , ${\nabla v(p)=0}$ , and ${\partial_n v(x) \leq 0}$ for all ${x \in \partial \Omega}$ (excluding vertices), but ${\partial_n v}$ is not identically zero on ${\partial \Omega}$ . Then ${u_2}$ does not have a critical point at at ${p}$ .

Proof: Suppose for contradiction that ${\nabla u_2(p)=0}$ . We first eliminate a degenerate case when ${u_2(p)=0}$ . In this case the nodal curve of ${u_2}$ crosses itself at ${p}$ , which by Corollary 4 creates at least four nodal domains, contradicting the Courant nodal line theorem. Thus we may assume without loss of generality that ${u_2(p)>0}$ . If we subtract a suitable multiple of ${v}$ from ${u_2}$ we then get another solution ${u}$ to the eigenfunction equation ${\Delta u = - \mu_2 u}$ with ${u(p)=\nabla u(p)=0}$ , and ${\partial_n u(x) \geq 0}$ on ${\partial \Omega}$ . Again, from Corollary 4 ${u}$ has at least four nodal domains, including at least two in which ${u}$ is negative. But this contradicts Corollary 3. $\Box$

Miyamoto uses this corollary with ${v}$ being a radial solution to the eigenfunction equation centered at ${p}$ to establish the hot spots conjecture for sufficiently round domains, but perhaps one can adapt the method to other solutions to also cover many cases of critical points inside various triangles.

Comments (6)

6 Comments »

Here is a computation building upon Siudeja’s arguments (Corollary 6 in the above post) that may possibly be helpful in strengthening that result.

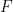Consider an acute triangle ABC, and let $\omega$ be the inward normal from AB towards C. Then the directional derivative $\partial_\omega u_2 = \omega \cdot \nabla u_2$ vanishes at AB and at C, as well as at any other critical point of $u_2$ , and solves the eigenfunction equation. Let $F$ be a nodal domain of $\partial_\omega u_2$ , and consider the quantity

${\mathcal H}_{\mu_2}( \partial_\omega u_2 1_F ).$ (*)

This is non-negative for all but at most one of the nodal domains (Lemma 1). On F, this quantity is equal to

$\int_{\partial F \cap \partial \Omega} \partial_\omega u_2 \cdot \partial_n \partial_\omega u_2$

(Corollary 3). The set $\partial F \cap \partial \Omega$ is the union of various intervals in AB, BC, AC, whose endpoints are boundary critical points of $u_2$ . The portion on AB vanishes because $\partial_\omega u_2$ vanishes here. Now consider an interval PQ on AC (with P closer to A than Q) of this set:

$\int_{PQ} \partial_\omega u_2 \partial_n \partial_\omega u_2$ .

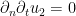We may write $\partial_\omega = \sin \alpha \partial_n + \cos \alpha \partial_t$ , where $\partial_t$ is the tangential derivative in the direction from A to C, and $\alpha$ is the angle $\alpha = \angle BAC$ . Using the Neumann condition $\partial_n u_2 = 0$ (which implies $\partial_n \partial_t u_2 = 0$ ), the above integral becomes

$\sin \alpha \cos \alpha \int_{PQ} \partial_t u_2 \partial_{nn} u_2$ .

On the other hand, from the eigenfunction equation we have $\partial_{nn} u_2 = - \partial_{tt} u_2 - \mu_2 u_2$ , so this integrates to

$-\frac{1}{2} \sin \alpha \cos \alpha ( \partial_t u_2^2 + u_2^2 )|^Q_P.$

As $P,Q$ are critical points of $u_2$ , $\partial_t u_2$ vanishes there, and so

$\int_{PQ} \partial_\omega u_2 \cdot \partial_n \partial_\omega u_2 = \frac{1}{2} \sin \alpha \cos \alpha ( u_2(P)^2 - u_2(Q)^2 ).$

We thus have a relatively simple formula for the quantity (*):

$(*) = \frac{1}{2} \sin \alpha \cos \alpha \sum_i (u_2(P_i)^2 - u_2(Q_i)^2) + \frac{1}{2} \sin \beta \cos \beta \sum_j (u_2(R_j)^2 - u_2(S_j)^2)$

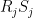where $P_i Q_i$ are the intervals of AC on the boundary of F, and $R_j S_j$ are the intervals of BC on the boundary of F.

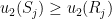If we consider a nodal domain on which $\partial_\omega u_2$ is positive, then we have $u_2(Q_i) \geq u_2(P_i)$ and $u_2(S_j) \geq u_2(R_j)$ . Unfortunately this doesn’t quite give a sign for (*) because $u_2$ can be both positive and negative. But perhaps we can control how the nodal curve of $\partial_\omega u_2$ interacts with the nodal curve of $u_2$ using this sort of analysis.

Note also that if u changes sign on, say, AC, then it must have an even number of critical points on the interior of AC, since it is a local maximum on A and a local minimum on C or vice versa. So if the hypotheses of Corollary 6 break down, then there are quite a few critical points on the boundary and so there should be quite a few nodal domains for $\partial_\omega u_2$ , which one can hopefully use to one’s advantage.

Comment by Terence Tao — August 9, 2013 @ 8:36 pm | Reply
Another thought that just occurred to me is that degree theory should be able to relate the number (or at least the parity) of the critical points in the interior with the critical points on the boundary, basically by trying to see how the gradient $\nabla u_2$ winds around the origin. If the hot spots conjecture is true, then if one traverses a loop in the triangle ABC that is very close but not quite touching the boundary (so as to avoid all the critical points at vertices and edges), the gradient of the eigenfunction should have a total winding number of zero, because there are no critical points in the interior. This should be equivalent to some assertion about the number of critical points on the boundary at points where the eigenfunction is positive or negative; I’ll try to work this out now (note that we can eliminate the degenerate critical points where the second derivative vanishes or where the solution vanishes).

Comment by Terence Tao — August 9, 2013 @ 11:00 pm | Reply
- OK, here is what degree theory tells us: assuming that critical points are always non-degenerate in the sense that the Hessian has non-zero determinant, the number of local extrema plus the number of saddle points in the triangle ABC must equal zero, where a critical point on an edge only counts for half, and a critical point at a vertex of angle $\alpha$ only counts for $\alpha/2\pi$ . In particular, for a second eigenfunction that is non-zero at the three vertices, all three vertices contribute a net of half of a local extremum, which must therefore be balanced by a net of half of a saddle point. Numerically, this comes from half of a saddle point on the edge connecting the two vertices where the eigenfunction does not change sign, and no other critical points. A local extremum in the interior of the triangle must then be balanced either by a saddle point in the interior, or two half-saddle points on the edges in addition to the half-saddle point that already must necessarily occur on the edge where the eigenfunction does not change sign.
  
  Unfortunately, it’s a bit tricky to figure out which critical points are local extrema and which are saddles; the former occurs when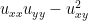 $u_{xx} u_{yy} - u_{xy}^2$ is positive and the latter when it is negative, and the eigenfunction equation 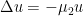$\Delta u = - \mu_2 u$ isn’t of much use in simplifying this constraint. (But on an edge, any positive local minimum or negative local maximum is necessarily a half-saddle point.)
  
  Comment by Terence Tao — August 9, 2013 @ 11:48 pm | Reply
Not much progress to report, unfortunately, but two small additional thoughts:

(a) now that narrow triangles have been dealt with, the other troublesome region of the configuration space is the nearly equilateral triangles (the region near the point H in the above diagram), mainly due to the fact that the second and third Neumann eigenvalue are very close to each other here (so that our previous numerical strategies would break down). Abstractly we know that there is an open region around H where the hot spots conjecture holds, but it may now be worthwhile to try to see how explicitly large of a region we can make here. One nice thing here is that for the perfectly equilateral triangle, all the spectral statistics (e.g. the Neumann eigenvalues, the Dirichlet eigenvalues, the mixed Neumann-Dirichlet eigenvalues when some sides are Neumann and others are Dirichlet) are all explicitly computable through reflection arguments and Fourier analysis, and through Rayleigh quotient arguments one can then get approximate control on these same statistics for nearly equilateral triangles.

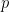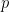(b) Miyamoto’s method proceeds by starting with the second eigenfunction $u_2$ with a critical point at $p$ , and subtracting off of it some multiple of an explicit solution $v$ to the eigenfunction equation with a critical point at $p$ with a definite sign on the normal derivative, to obtain a new solution with a degenerate critical point and a definite sign on the normal derivative, which can then be used to lead to a contradiction. But it might be possible to get additional information on $u_2$ by finding other ways to line up $u_2$ and $v$ to create a degenerate critical point. For instance, instead of getting the critical points of $u_2$ and $v$ to line up, one could ask instead for the nodal lines of $u_2$ and $v$ to be tangent to each other, as this would also mean that some linear combination of $u_2, v$ have a degenerate critical point (cf. the Lagrange multiplier method). Similarly if $u_2/v$ has a critical point at some point other than the nodal line of $v$ . By playing around with various choices for $v$ (e.g. radial examples, whose nodal line is a circle, or cosine examples, whose nodal line is a line) this may provide some geometric constraints on the nodal line which could potentially be useful. (For instance we had a conjecture that the nodal line was convex, which might potentially be attackable by this sort of method.) In conjunction with point (b), we might try all this first for the equilateral triangle, where the nodal lines are explicitly computable and the geometry is all explicit and symmetric.

Comment by Terence Tao — August 13, 2013 @ 8:41 pm | Reply
- Sorry, I’ve been bogged down by assorted other things and hope to return to posting some code+results within a few weeks.
  
  Your comment (a) reminds me: computing the spectral gap in the neighbourhood of the equilateral triangles, I recall observing that there was a striking difference (in terms of symmetries) between the variation of the second (ie, first non-zero) eigenvalue with triangle angles, and the variation of the third eigenvalue angles. Perhaps this is a well-known fact in spectral analysis? Here are (coarse grid) figures of what I mean:
  
  Figure of the second Neumann eigenvalue as a function of triangle angles:
  
  Figure of the third Neumann eigenvalue as a function of triangle angles (sorry, figure title has a typo.)
  
  I wondered if this observation could somehow be used in trying to establish (a)? I used this informally to help me decide how to refine grids in parameter space.
  
  Comment by nilimanigam — September 9, 2013 @ 7:55 pm | Reply
The following new arXiv preprint by Judge and Mondal appears to affirmatively resolve the hot spots conjecture for triangles: https://arxiv.org/abs/1802.01800

Comment by Terence Tao — February 8, 2018 @ 12:05 am | Reply

RSS feed for comments on this post. TrackBack URI

	Cherrypick India on Polymath projects 2021
	tanner808 on Polymath projects 2021
	Anonymous on Polymath 11 is Now Open
	Chenxiao Tian on Polymath 11 is Now Open
	ryeguy10 on Polymath 11 is Now Open
	ndnnnd on Polymath projects 2021
	Prime time on Two polymath (of a sort) propo…
	What comes after exp… on Minipolymath2 project: IMO 201…
	Will AI Replace Math… on Spontaneous Polymath 14…
	gui7575 on A new polymath proposal (relat…
	Thomas Vu on Polymath projects 2021
	Mary Megrant on Polymath projects 2021
	h0sane on A sort of Polymath on a famous…
	Thomas Vu on Polymath projects 2021
	Hyun seok on A sort of Polymath on a famous…

The polymath blog

August 9, 2013