This post marks the official opening of the mini-polymath2 project to solve a problem from the 2010 IMO. I have selected the fifth question (which appears to be slightly more challenging than the sixth, for a change) as the problem to focus on:
Problem. In each of six boxesthere is initially one coin. There are two types of operation allowed:
- Type 1: Choose a nonempty box
with
. Remove one coin from
and add two coins to
.
- Type 2: Choose a nonempty box
with
. Remove one coin from
and exchange the contents of (possibly empty) boxes
and
.
Determine whether there is a finite sequence of such operations that results in boxesbeing empty and box
containing exactly
coins. (Note that
.)
The comments to this post shall serve as the research thread for the project, in which participants are encouraged to post their thoughts and comments on the problem, even if (or especially if) they are only partially conclusive. Participants are also encouraged to visit the discussion thread for this project, and also to visit and work on the wiki page to organise the progress made so far.
This project will follow the general polymath rules. In particular:
- All are welcome. Everyone (regardless of mathematical level) is welcome to participate. Even very simple or “obvious” comments, or comments that help clarify a previous observation, can be valuable.
- No spoilers! It is inevitable that solutions to this problem will become available on the internet very shortly. If you are intending to participate in this project, I ask that you refrain from looking up these solutions, and that those of you have already seen a solution to the problem refrain from giving out spoilers, until at least one solution has already been obtained organically from the project.
- Not a race. This is not intended to be a race between individuals; the purpose of the polymath experiment is to solve problems collaboratively rather than individually, by proceeding via a multitude of small observations and steps shared between all participants. If you find yourself tempted to work out the entire problem by yourself in isolation, I would request that you refrain from revealing any solutions you obtain in this manner until after the main project has reached at least one solution on its own.
- Update the wiki. Once the number of comments here becomes too large to easily digest at once, participants are encouraged to work on the wiki page to summarise the progress made so far, to help others get up to speed on the status of the project.
- Metacomments go in the discussion thread. Any non-research discussions regarding the project (e.g. organisational suggestions, or commentary on the current progress) should be made at the discussion thread.
- Be polite and constructive, and make your comments as easy to understand as possible. Bear in mind that the mathematical level and background of participants may vary widely.
Have fun!
[…] July, 2010 in admin, polymath | by Terence Tao I’ve just opened the Mini-polymath2 project over at the polymath blog. I decided to use Q5 from the 2010 IMO in the end, rather than Q6, as […]
Pingback by Mini-polymath2 discussion thread « What’s new — July 8, 2010 @ 3:56 pm |
[…] collaboratively but have been intimidated by the difficulty of the problems, I recommend the Minipolymath2 project which has just started and involves an intriguing puzzle with coins and boxes. All ability levels […]
Pingback by Mini-polymath project #2 « The Number Warrior — July 8, 2010 @ 4:10 pm |
By the first rule we can say that a coin in B_6 is worth 1, a coin in B_5 is worth 2, …, a coin in B_1 is worth 32. By applying the second rule in certain situations the total worth of the boxes may go up (when B_(j+2) has four more coins than B_j). It seems plausible, then, that we might be able to get an arbitrarily high “total worth.”
Comment by Aaron Hill — July 8, 2010 @ 4:13 pm |
– more precisely, the total worth goes up when .
.
Comment by Greg — July 8, 2010 @ 4:19 pm |
Trivial observation:
whenever the left-most box becomes empty, it cannot be filled again
Comment by oz — July 8, 2010 @ 4:14 pm |
This seems to imply that we cannot get arbitrarily high “total worth.” If I use the coin in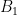 then this box will never have another coin in it. If I have already used the coin in
then this box will never have another coin in it. If I have already used the coin in 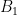 (or decide to “save” this coin for further use, then the same should apply to the coin in
(or decide to “save” this coin for further use, then the same should apply to the coin in 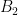 (I can only use it once). This seems to go on (I’m not sure exactly how it goes) to show that we can’t get an arbitrarily high “total worth.” Can we find a specific bound?
(I can only use it once). This seems to go on (I’m not sure exactly how it goes) to show that we can’t get an arbitrarily high “total worth.” Can we find a specific bound?
Comment by Aaron Hill — July 8, 2010 @ 4:35 pm |
We can probably construct some sort of recursive formula for maximal # of coins in a given box. For example, we can use the coin in B_1 obtain B_2 with 3 coins, or use just boxes B_2,…,B_6 (i.e. a five-box variant of our problem) to get as many coins as possible in B_3 and then exchange B_2 and B_3.
Comment by Alexandr Kazda — July 8, 2010 @ 4:45 pm |
Another trivial observation: The first box will always contain at most one coin (there is no way to fill it).
It might be useful to calculate the maximal number of coins we can put in boxes two through six.
Comment by Alexandr Kazda — July 8, 2010 @ 4:37 pm |
I think the first three numbers here are 1, 3, 7. Can we do better than 22 in B_4?
Comment by Aaron Hill — July 8, 2010 @ 4:44 pm |
Yes, it seems to me that the numbers grow ‘too slow’, but maybe something radically different
happens at the fifth or sixth box. How can you get 22 in B_4? (the best I could find was 19)
Comment by oz — July 8, 2010 @ 4:51 pm |
With some uses of rule 1 (R) we get to [0,1,0,11] Then using rule 2 (S) we get [0,0,11,0]. Then with some uses of R we get [0,0,0,22]
Comment by Aaron Hill — July 8, 2010 @ 5:15 pm |
It might be worth building simple primitive procedures/functions (in the software sense). For example:
![[1, X, Y] \mapsto [0, 0, X+2Y]](https://s0.wp.com/latex.php?latex=%5B1%2C+X%2C+Y%5D+%5Cmapsto+%5B0%2C+0%2C+X%2B2Y%5D&bg=ffffff&fg=000000&s=0&c=20201002) (apply the first rule once and then the second rule Y times)
(apply the first rule once and then the second rule Y times)
Comment by oz — July 8, 2010 @ 4:18 pm |
Minor correction: one applies the Type 2 rule once and then Type 1 rule Y times.
It seems worthwhile to have a systematic notation for these sorts of moves, for instance Type 1 is![[X,Y] \to [X-1,Y+2]](https://s0.wp.com/latex.php?latex=%5BX%2CY%5D+%5Cto+%5BX-1%2CY%2B2%5D&bg=ffffff&fg=000000&s=0&c=20201002) and Type 2 is
and Type 2 is ![[X,Y,Z] \to [X-1,Z,Y]](https://s0.wp.com/latex.php?latex=%5BX%2CY%2CZ%5D+%5Cto+%5BX-1%2CZ%2CY%5D&bg=ffffff&fg=000000&s=0&c=20201002) (bearing in mind, of course, that one is not allowed to have a negative number of coins).
(bearing in mind, of course, that one is not allowed to have a negative number of coins).
Comment by Terence Tao — July 8, 2010 @ 4:33 pm |
Can we first get one thing out of the way and prove that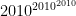 is not “too large”, i.e. some value greater than or equal to it can be attained?
is not “too large”, i.e. some value greater than or equal to it can be attained?
(This may not be much help in proving that the exact value can be attained, but it would overcome the most surprising-at-first-sight thing about the question, which is that we may be able to get so large a value starting with just 6 coins.)
Comment by svat — July 8, 2010 @ 4:33 pm |
Yes, we can. See comment thread 13 below: it seems to shows that we can do
![[1, 1, 1, 1, 1, 1] \to [0, 0, 7, 1, 1, 1] \to [0, 0, 7, 1, 0, 3] \to [0, 0, 6, 1, 0, 2^3] \to [0, 0, 5, 1, 0, 2^{2^3}] \to \dots \to [0, 0, 0, 1, 0, 2^{2^{2^{2^{2^{2^{2^3}}}}}}].](https://s0.wp.com/latex.php?latex=%5B1%2C+1%2C+1%2C+1%2C+1%2C+1%5D+%5Cto+%5B0%2C+0%2C+7%2C+1%2C+1%2C+1%5D+%5Cto+%5B0%2C+0%2C+7%2C+1%2C+0%2C+3%5D+%5Cto+%5B0%2C+0%2C+6%2C+1%2C+0%2C+2%5E3%5D+%5Cto+%5B0%2C+0%2C+5%2C+1%2C+0%2C+2%5E%7B2%5E3%7D%5D+%5Cto+%5Cdots+%5Cto+%5B0%2C+0%2C+0%2C+1%2C+0%2C+2%5E%7B2%5E%7B2%5E%7B2%5E%7B2%5E%7B2%5E%7B2%5E3%7D%7D%7D%7D%7D%7D%5D.&bg=ffffff&fg=000000&s=0&c=20201002) And the next thread has ideas on reducing the number of coins once we have enough.
And the next thread has ideas on reducing the number of coins once we have enough.
Comment by svat — July 8, 2010 @ 6:37 pm |
Could the following approach work? Get a number larger than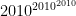 which I will call
which I will call  in one of the first
in one of the first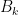 then then exchange the contents of
then then exchange the contents of 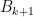 and
and 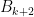 till there are the right number of coins in
till there are the right number of coins in 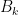 . Note to do this we must also get the other boxes empty. That leaves the question of constructing an arbitrarily large number.
. Note to do this we must also get the other boxes empty. That leaves the question of constructing an arbitrarily large number.
four cans
Comment by Kristal Cantwell — July 8, 2010 @ 4:37 pm |
Yes, it looks like it is relatively easy to remove coins from the system, but difficult to add coins to the system. This suggests splitting the problem into two subproblems if one wants to solve the problem affirmatively:
Subproblem 1: Show that one can have arbitrarily many coins in the system.
Subproblem 2: Given that one can find a state with arbitrarily many coins, obtain a state in which the first five boxes are empty and the last box contains coins.
coins.
To solve the problem negatively, it does seem the best approach would be to give a negative answer to Subproblem 1 in a sufficiently quantitative fashion.
Comment by Terence Tao — July 8, 2010 @ 4:47 pm |
First thought on solving Subproblem 1 was to find a loop in the system; some set of operations that returns boxes 1..k to their initial position, but increases k+1. However, that seems impossible to me, given the nature of the operations. There is no way to increase a later box without decreasing an earlier one.
Is that obvious enough that we can state it as fact? And if so, is there any route left by which we could possibly create an arbitrary number of coins in the system?
Comment by josh g. — July 8, 2010 @ 5:16 pm |
I suppose my imagination may simply be failing me … we could have an infinite sequence which does not return earlier boxes to their exact state, but still increases the system arbitrarily high.
Comment by josh g. — July 8, 2010 @ 5:31 pm |
Is it easy to see how to get a number larger than ? Another direction is maybe to look at obstacles in obtaining ‘certain’ numbers.
? Another direction is maybe to look at obstacles in obtaining ‘certain’ numbers.
Comment by Yu — July 8, 2010 @ 4:49 pm |
Some obvious points:
1) Slot one will never have more than one coin.
2) Slot two will never have more coins that slot three can have (since it can get the most coins through a swap with three).
Comment by Mike — July 8, 2010 @ 5:05 pm |
Could the operations be referred to by something like 1n for rule one applied to box n and 2m for rule two applied to box m?
That would seem to simplify things.
Comment by Kristal Cantwell — July 8, 2010 @ 4:44 pm |
Maybe R1n and R2m?
Comment by Aaron Hill — July 8, 2010 @ 4:46 pm |
Notation-wise, because the box numbers are also integers, it may be clearer to call the rules A and B. :-)
Comment by soho — July 8, 2010 @ 5:05 pm |
So “A3” means apply rule number 1 to B_3 and “B1” means apply rule number 1 to B_1? Uh oh, two different B’s. Maybe “R” for Rule number 1 and “S” for rule number 2?
Comment by Aaron Hill — July 8, 2010 @ 5:11 pm |
I can get![[1,1,1] \to [0,0,7]](https://s0.wp.com/latex.php?latex=%5B1%2C1%2C1%5D+%5Cto+%5B0%2C0%2C7%5D&bg=ffffff&fg=000000&s=0&c=20201002) , using just Rule 1.
, using just Rule 1.
Or![[N,0,0] \to [N-1,0,4] \to [N-2,0,8] \to \to [0,0,2^{N+1}]](https://s0.wp.com/latex.php?latex=%5BN%2C0%2C0%5D+%5Cto+%5BN-1%2C0%2C4%5D+%5Cto+%5BN-2%2C0%2C8%5D+%5Cto+%5Cto+%5B0%2C0%2C2%5E%7BN%2B1%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Then![[28,1,1] \to [27,0,7] \to [0,0,7*2^{27}]](https://s0.wp.com/latex.php?latex=%5B28%2C1%2C1%5D+%5Cto+%5B27%2C0%2C7%5D+%5Cto+%5B0%2C0%2C7%2A2%5E%7B27%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , which is way below what is needed.
, which is way below what is needed.
Comment by Michael — July 8, 2010 @ 4:50 pm |
Can you please use commas to separate the amounts in different boxes? [Fixed – T.] It would make your text easier to read. Also, I think that![[27,0,7] \mapsto [0,0,7+4*27]](https://s0.wp.com/latex.php?latex=%5B27%2C0%2C7%5D+%5Cmapsto+%5B0%2C0%2C7%2B4%2A27%5D&bg=ffffff&fg=000000&s=0&c=20201002) , which is a lot less than
, which is a lot less than  .
.
Comment by Alexandr Kazda — July 8, 2010 @ 4:55 pm |
Sorry, I meant![[27,0,7] \to [26,7,0] \to [26,0,14] \to [25,14,0] \to [25,0,28]](https://s0.wp.com/latex.php?latex=%5B27%2C0%2C7%5D+%5Cto+%5B26%2C7%2C0%5D+%5Cto+%5B26%2C0%2C14%5D+%5Cto+%5B25%2C14%2C0%5D+%5Cto+%5B25%2C0%2C28%5D&bg=ffffff&fg=000000&s=0&c=20201002) and so on. Use a single coin from
and so on. Use a single coin from 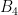 to shift
to shift 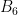 coins into
coins into 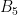 , then double them all back into
, then double them all back into 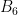 .
.
Comment by Michael — July 8, 2010 @ 5:04 pm |
How does one get to![[0,0,2^{N+1}]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C2%5E%7BN%2B1%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) in the second line? to me it seems you get to
in the second line? to me it seems you get to ![[0,0,4*N]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C4%2AN%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Comment by oz — July 8, 2010 @ 5:01 pm |
Oh sorry, I got it now (you could use just rule 1 to get 4 and 8, but for 16 you need rule 2)
Comment by oz — July 8, 2010 @ 5:07 pm |
I think I understood Michael’s first line: In the place where there are two arrows at the end, we go by [N-2,0,8] -> [N-3,8,0] -> [N-3,0,16] -> etc. Using the coin from the first box to effectively double the amount in the third box.
We can probably do even better with four boxes (something like 2^{2^N} maybe?).
Comment by Alexandr Kazda — July 8, 2010 @ 5:10 pm |
With four boxes, we can go (using Michael’s special move):
![[N,0,0,0]\to [1,0,2^N,0]\to [1,0,2^N-1,2]\to[0,2^N-1,0,2]\to[0,0,2^{2^N}]](https://s0.wp.com/latex.php?latex=%5BN%2C0%2C0%2C0%5D%5Cto+%5B1%2C0%2C2%5EN%2C0%5D%5Cto+%5B1%2C0%2C2%5EN-1%2C2%5D%5Cto%5B0%2C2%5EN-1%2C0%2C2%5D%5Cto%5B0%2C0%2C2%5E%7B2%5EN%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Comment by Alexandr Kazda — July 8, 2010 @ 5:27 pm |
Or, to simplify, we can have the following basic move: [N,0,0]->[1,0,2^N]->[0,2^N,0],
so essentially the move is [N,0]->[0,2^N], except it cannot be used on the last boxes [B_5,B_6]
Comment by oz — July 8, 2010 @ 5:49 pm |
Well, that’s already moderately large, which gives us hope…
I’ve started a section on the wiki for “World records” on how large one can get various boxes, and added the above.
I’ve also started a section on “advanced moves” that are compositions of the two basic moves. It does seem worthwhile to have some sort of library of useful moves, particularly those that grow the number of coins rapidly. I encourage others to add to these lists.
Comment by Terence Tao — July 8, 2010 @ 5:04 pm |
Polya says if you can’t answer a question, try to find an easier question you might(!) be able to answer. I don’t know what strategy to use if there are 6 boxes (with some initial number of coins in each box) and I want to maximize total worth. Maybe I can find out what strategy to use if there are only 3 boxes that start with A, B, and C, coins respectively.
Comment by Aaron Hill — July 8, 2010 @ 4:56 pm |
Yes, isn’t it equivalent to trying to maximize the number of coins in B_1, B_2 etc.?
for this you gave 1, 3, 7 and for B_4 the above comment by Michael gives 28
Comment by oz — July 8, 2010 @ 5:03 pm |
Not sure if this helps yet, but at some point we might think about working backwards: steps. Then the next-to-last step,
steps. Then the next-to-last step,  , would either have to be:
, would either have to be:
Let’s say there is a solution and it takes
(Rule 1) 1 coin in B5, in B6, and 0 elsewhere; or
in B6, and 0 elsewhere; or
(Rule 2) 1 coin in B4,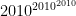 in B5, and 0 elsewhere.
in B5, and 0 elsewhere.
If it’s Rule 2, then the step before *that*, i.e. (M-2), would have to have been one of the two options above but shifted once to the left… so it’d be just like solving the same puzzle but with only 5 boxes.
So it seems unlikely that the last few steps of the solution could be using Rule 2 several times in a row; otherwise we could solve the puzzle with fewer boxes, which doesn’t look promising.
Comment by Jerzy Wieczorek — July 8, 2010 @ 5:00 pm |
The “total worth” of the boxes remains unchanges by rule number one. It is less than doubled by rule number two. So, as the total worth of the desired result is so large, any way to get their would take an enormous number of steps. PS how do I do latex in here? [See https://polymathprojects.org/how-to-use-latex-in-comments/ – T.]
Comment by Aaron Hill — July 8, 2010 @ 5:06 pm |
Whoops—actually, if the (M-1) step was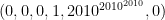 , that’s not actually equivalent to solving the problem with just 5 boxes. Here we do have 1 coin in B6 to start with, so we couldn’t just solve this with the first 5 boxes alone and then use Rule 2 on B4—that would leave us with 1 coin in B5. My bad. So just to get to the state
, that’s not actually equivalent to solving the problem with just 5 boxes. Here we do have 1 coin in B6 to start with, so we couldn’t just solve this with the first 5 boxes alone and then use Rule 2 on B4—that would leave us with 1 coin in B5. My bad. So just to get to the state 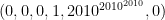 we’d have to have somehow used B6 previously.
we’d have to have somehow used B6 previously.
Comment by Jerzy Wieczorek — July 8, 2010 @ 5:16 pm |
As another simplification of the problem that might be instructive, try starting ith just one coin in B1 and none in the other boxes. What can be done then?
Comment by PhilG — July 8, 2010 @ 5:18 pm |
Let’s see: from [1, 0, 0, 0, 0, 0]: you can empty the system entirely via Rule 2 (getting to [0,0,0,0,0,0])
or you can use Rule 1 to give us
[0, 2, 0, 0, 0, 0].
Assuming that we want to make things as large as possible (i.e. no emptying the system), our natural best guess would be to use Rule 1 again, yielding
[0, 1, 2, 0, 0, 0]. From there we could use Rule 1 twice and then Rule 2 once to get [0, 0, 4, 0, 0, 0].
After that: [0, 0, 3, 0, 4, 0] –> [0, 0, 2, 4, 0, 0] –> [0, 0, 1, 8, 0, 0] –> [0, 0, 0, 16, 0, 0]… which, by previous arguments, can get us to 2^17 = 131072 in Box 6 – but no larger!
Comment by mmailliw/william — July 8, 2010 @ 6:16 pm |
Five starter coins give me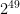 coins this way:
coins this way:
Comment by Michael — July 8, 2010 @ 5:20 pm |
You make the choice to immediately use the leftmost 1 (which I think is a good choice). What can be said about the general situation [a, b, c, d]? What are the strategies or useful move sequences when we have four boxes?
Comment by Aaron Hill — July 8, 2010 @ 5:25 pm |
Clearly you can get even more by moving all of these to the sixth spot, so you’ll get 2^2^49.
Comment by Mike — July 8, 2010 @ 5:29 pm |
Wait, I’m sorry, that’s not right.
Comment by Mike — July 8, 2010 @ 5:38 pm |
For example, the strategy you (Michael) used at the end is [A, 0, 0] goes to [0, 0, 2^(A+1)].
Comment by Aaron Hill — July 8, 2010 @ 5:30 pm |
Strategy for starting with [A, 0, 0, 0] for A not two small: Apply rule number 1 (a few times) to get [A-2, 1, 0, 12]. Apply rule number 2 (a few times) to get [A-3, 12, 0, 0]. Apply rule 1 to get [A-3, 1, 0, 2^12]. Apply rule 2 to get [A-4, 2^12, 0, 0]. Apply rule 1 to get [A-4, 1, 0, 2^(2^12)]. Continue. The final result is [0, 1, 0, 2^2^2^… 2^12], where there are A-2 twos in the tower.
Comment by Aaron Hill — July 8, 2010 @ 5:44 pm |
If I am not mistaken this allows (in the original problem with 6 box) to get 2^2^2^2^2^2^2^3 number of coins in box B_6. It goes like this:
![[1, 1, 1, 1, 1, 1] \rightarrow [0,0,7,1,1,1] \rightarrow [0,0,7,1,0,3] \rightarrow [0,0,6,1,0,2^3]](https://s0.wp.com/latex.php?latex=%5B1%2C+1%2C+1%2C+1%2C+1%2C+1%5D+%5Crightarrow+%5B0%2C0%2C7%2C1%2C1%2C1%5D+%5Crightarrow+%5B0%2C0%2C7%2C1%2C0%2C3%5D+%5Crightarrow+%5B0%2C0%2C6%2C1%2C0%2C2%5E3%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Comment by Aaron Hill — July 8, 2010 @ 5:55 pm |
Sorry about this: [1, 1, 1, 1, 1, 1] goes to [0, 0, 7, 1, 1, 1] goes to [0, 0, 7, 1, 0, 3] goes to [0, 0, 6, 1, 0, 2^3] goes to [0, 0, 5, 1, 0, 2^2^3] goes to … goes to [0, 0, 0, 1, 0, 2^2^2^2^2^2^2^3].
Comment by Aaron Hill — July 8, 2010 @ 5:59 pm |
Aaron, I didn’t check your logic thoroughly, but if it’s right, then bounding is not going to be a problem since 2010^2010^2010 is bounded by 2^2^2^2^4.
2010^2010^2010 = 2^(log2(2010)*2010^2010)
= 2^2^(2010*log2(2010)+log2(log2(2010)))
< 2^2^(2010*11+log2(11))
< 2^2^(22114)
< 2^2^2^15
< 2^2^2^2^4
So if you’re right, that means we can get [0, 1, 0, 2^2^2^2^4] starting with [2, 0, 0, 0] which is certainly possible here.
So now it just becomes a question of whether we can get exactly the desired number.
Comment by Jerzy Wieczorek — July 8, 2010 @ 6:05 pm |
Lets make sure that this checks out (so if you read this please double check it): Lemma: If we have something like [A, 1, 0, n] then we can get [A-1, 1, 0, 2^n].
Proof: S2 (switch using a coin from box 2) gives [A, 0, n, 0]. S1 gives [A-1, n, 0, 0]. Some D2’s and D3’s (doubles) gives [A-1, n-2,0 8 ]. S2 gives [A-1, n-3, 8, 0]. Some D3’s give [A-1, n-3, 0, 16]. S2 gives [A-1, n-4, 16, 0]. Some D3’s give [A-1, n-4, 0, 32]. Continue and you will get [A-1, 1, 0, 2^n].
Comment by Aaron Hill — July 8, 2010 @ 6:37 pm |
Now lets use the Lemma repeatedly:
We start with [1, 1, 1, 1, 1, 1]. A D1 and three D2’s gives [0, 0, 7, 1, 1, 1], which we will write as [7, 1, 1, 1]. D3 (which corresponds to the original D5) gives [7, 1, 0, 3]. Use the lemma 7 times and we get [0, 1, 0, 2^2^2^2^2^2^2^3]. Then with a D2 and two D3s we get [0, 0, 0, 4 + 2^2^…2^3].
Comment by Aaron Hill — July 8, 2010 @ 6:49 pm |
So instead of using the lemma 7 times, only use it 6 times. Then you have [1, 1, 0, 2^2^2^2^2^2^3]. Swap, and you get [1, 0, 2^2^2^2^2^2^3, 0] Swap again, and you get [0, 2^2^2^2^2^2^3, 0, 0]. Swap as many times as needed until you get (2010^2010^2010)/4, then push it to slot 6.
The only thing to check is that 2^2^2^2^2^2^2^3 is greater than 2010^2010^2010, which was checked above for 2^2^2^2^4.
Comment by Mike — July 8, 2010 @ 7:19 pm |
If we want to try to prove that the task is not possible, it might be worthwhile to give a value to a coin in box i as something larger than , for example,
, for example,  . This way, move 1 decreases the value, and it becomes much harder to increase the value using move 2. It may then be possible to then show that, if the value is below some critical level, it will always remain below that critical level.
. This way, move 1 decreases the value, and it becomes much harder to increase the value using move 2. It may then be possible to then show that, if the value is below some critical level, it will always remain below that critical level.
Comment by Aaron — July 8, 2010 @ 5:26 pm |
Could this work as a solution?
Step One.
Move everything to box 5.
Step 2.
add one coin from box 5 to box 6.
interchange box 5 and 4.
Step 3
add one coin from box 4 to box 5.
interchange box 3 and 4.
Step 4
add one coin from box 3 to box 4.
interchange box 2 and 3.
Step 5
add one coin from box 2 to box 3.
interchange box 1 and 2.
Go back to step 1. Repeat until we have a number greater than 2010^{2010^{2010}}
Then move everything to box 6.
Then interchange the empty boxes 4 and 5 until box 6
has the desired number of coins.
Comment by Kristal Cantwell — July 8, 2010 @ 5:27 pm |
No I don’t think this works. I think I have rule 2 wrong.
Comment by Kristal Cantwell — July 8, 2010 @ 5:32 pm |
Once everything is in box 5, you can no longer do Step 2. You’d need a coin left in box 3 to be allowed to interchange boxes 4 and 5.
Comment by josh g. — July 8, 2010 @ 5:35 pm |
Dear all,
I suggest the following “maximal” approach to show that the total number of coins in the system is bounded.
0. Let us call operations that consume a coin in box k
of type 1: “D_k” (for “double”)
of type 2: “S_k” (for “swap”)
and let n_k the number of coins in the box k
1. Define a partial ordering on the possible configurations comparing the number of coins box by box.
2. “S_k” and “D_k” are monotone with respect to this ordering, i.e. they map comparable configurations in comparable ones and preserve order.
3. Both “S_k” and “D_k” are bounded by the “maximal” operation “M_k” that decreases n_k by one and
for k<=4: sets n_{k+1} to n_{k+2} + 2 n_{k+1} + 2 and sets n_{k+2} to 0
for k=5: increases n_6 by 2.
Clearly, M_k followed by some instances of D_{k+1} majorizes both D_k and S_k. By descending induction on k, we see that D_{k+1} may be replaced by M_{k+1} in the former statement. Therefore, any combination of Ds and Ss is majorized by some combination of Ms.
4. Call the number of boxes N and the initial sum of numbers in them "Sigma". By ascending induction on N we will obtain an upper bound on the sum of numbers in the boxes in terms of N and Sigma, say f(N,Sigma).
A. f(2,Sigma) = 2 Sigma
B. One potentially obtains the greatest sum if all of Sigma is concentrated in the first box.
C. At some points in time, one will use M_1. By B, assume that, at this points, the numbers in boxes 3,4,… are zero (this is probably the crudest estimate in the argument!). Then, until the next use of M_1, the number in box 2 will rise at most to f(N-1, n_2).
D. Combining this with the definition of M_1, we have
f(N, Sigma) \leq f(N-1, 2+2*f(N-1, … +2*f(N-1, 2) … ),
with Sigma occurences of f(N-1, \cdot ). This gives a (horrible) explicit bound on f(6,6), which is the maximal sum obtainable in the problem.
Comment by pavel zorin — July 8, 2010 @ 5:30 pm |
It seems to me that the left-hand boxes are the most valuable ones to keep, and that working rhs first, keeping boxes 1 and 2 as long as possible could work well.
Comment by Mark Bennet — July 8, 2010 @ 5:37 pm |
There is a “soft” argument that shows that the number of possible coins is bounded, based ultimately on the fact that the lexicographical ordering in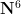 is a well-ordering. Jargon aside, it works like this:
is a well-ordering. Jargon aside, it works like this:
suppose that there was an infinite sequence of moves. Then the number of coins in the first box can only decrease, and must therefore eventually be constant. Once it is constant, the number of coins in the second box can only decrease, and must therefore eventually be constant. Iterating this we see that eventually all boxes must stay constant, i.e. there are no more moves available. So an infinite sequence of moves cannot occur. By Konig’s lemma, this implies that the total number of possible move sequences is finite, and so the total number of coins available is bounded.
Unfortunately this argument does not easily give any useful bound…
Comment by Terence Tao — July 8, 2010 @ 5:41 pm |
It looks like this can be generalized to give any finite number of coins in a finite number of boxes
has the total number of coins bounded.
Comment by Kristal Cantwell — July 13, 2010 @ 4:02 am |
I have a feeling the maximum number which can be achieved will be higher than c:=2010^2010^2010.
Can we use number theory to show that it is not possible? I.e. look at the binary expansion of c!?
On a different note, this problem begs for the introduction of a potential (just like as in Conway’s Angels and Demons).
Comment by JB Grenouille — July 8, 2010 @ 5:42 pm |
I wonder if there is an inductive way of setting an upper bound by showing that a function aN1 + bN2 + cN3 + dN4 + eN5 + fN6 always decreases assuming a maximum bound on each number N1, N2, N3, N4, N5, N6, here we pick the numbers a,b,c,d,e,f with each number much bigger than the following one
Comment by PhilG — July 8, 2010 @ 5:42 pm |
With six boxes, we can get (i.e.
(i.e.  ) coins in this way:
) coins in this way:
![[1,1,1,1,1,1]\to\to [0,0,7,1,1,1]\to [0,0,7,0,3,1]\to\to [0,0,1,0,3*2^6,1]\to [0,0,0,3*2^6,0,1]\to [0,0,0,0,0,2^{3*2^6}]](https://s0.wp.com/latex.php?latex=%5B1%2C1%2C1%2C1%2C1%2C1%5D%5Cto%5Cto+%5B0%2C0%2C7%2C1%2C1%2C1%5D%5Cto+%5B0%2C0%2C7%2C0%2C3%2C1%5D%5Cto%5Cto+%5B0%2C0%2C1%2C0%2C3%2A2%5E6%2C1%5D%5Cto+%5B0%2C0%2C0%2C3%2A2%5E6%2C0%2C1%5D%5Cto+%5B0%2C0%2C0%2C0%2C0%2C2%5E%7B3%2A2%5E6%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) where
where  are the special moves.
are the special moves.
Comment by Alexandr Kazda — July 8, 2010 @ 5:45 pm |
I think the answer to the problem is that we can get the desired number of coins in Box 6. It looks like we need a function that dominates the tower function in the Ackermann hierarchy. We just have to find the right recursion and prove that it works. Then the problem becomes more like a programming problem in trying to find functions that blow up quickly from small initial values.
Comment by Kristal Cantwell — July 8, 2010 @ 5:47 pm |
I think it is a great idea to work backwards, some sort of cyclic approach taking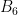 subtracting two coins, adding one to the previous box. The idea seems to have been left.
subtracting two coins, adding one to the previous box. The idea seems to have been left.
Comment by DA — July 8, 2010 @ 5:48 pm |
Random note: A strategy might be to end up with more than enough coins and then remove coins until you have the right amount in Slot 6. But if you end up stuck in spot 6 with more than enough stuff in the slot but zeroes everywhere else you’re stuck, since you have no moves to reduce it.
You’re likewise stuck if you end up with piles in slots 5 and 6, unless 6 is missing the correct amount of coins by precisely 2^n (where there are n coins in 5).
Comment by Mike — July 8, 2010 @ 5:54 pm |
I’m wondering whether the answer to the question might be no.
Might there be some invariant of the system that cannot possibly hold if Box 6 has 2010^2010^2010 coins?
Comment by mmailliw/william — July 8, 2010 @ 5:54 pm |
Just a reminder: we are now generating quite a few new world records and useful-looking advanced moves, together with other strategies and partial results; if you have the time, please put them on the wiki
http://michaelnielsen.org/polymath1/index.php?title=Imo_2010
so that they don’t get lost in the flood of comments!
Comment by Terence Tao — July 8, 2010 @ 5:57 pm |
Just throwing in another move:
And we can get [0,0, 140, 0, 0 ,0] as follows:
Comment by SM — July 8, 2010 @ 6:03 pm |
Sorry, how do I use LaTeX? [See https://polymathprojects.org/how-to-use-latex-in-comments/ – T.]
Comment by SM — July 8, 2010 @ 6:05 pm |
Let
So we can go at least as high as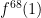 , that should be way above
, that should be way above 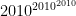 , right?
, right?
Comment by SM — July 8, 2010 @ 6:14 pm |
For 3 boxes (1,1,1) we can get to (0,0,7)
For 4 boxes (1,1,1,1) we can get to (0,0,0,28)
For 5 boxes (1,1,1,1,1) we can get to (1,0,0,0,28) using the right-hand-first rule
then A1 (0,2,0,0,28); A2 (0,1,2,0,28); B3 (0,1,1,28,0); A3?best (0,1,0,30,0); B2 (0,0,30,0,0)
Then A3 (0,0,29,2,0) A4 twice (0,0,29,0,4)
then repeats of (B3, followed by chunks of A4) take us to (0,0,0,0,4x[2^29])=(0,0,0,0,2^31)
And incidentally from (n,0,0) we can get to (0,0,2^(n+1))
Comment by Mark Bennet — July 8, 2010 @ 6:05 pm |
Still on 5
Where A3?best is try A4x28 (0,1,1,0,56); B3 (0,1,0,56,0); B2 (0,0,56,0,0)
then as before proceed to get (0,0,0,0,2^57)
Comment by Mark Bennet — July 8, 2010 @ 6:11 pm |
So we can get to at least [1,0,0,0,0,2^57]
and [1,0,0,0,n] gets us to [0,0,0,0,2^(2n+1)] at least (rule M, let’s say)
From [1,0,0,0,0,n] we get to [0,2,0,0,0,n]
Apply rule M once we get [0,1,0,0,0,2^(2n+1)]
And again [0,1,0,0,0,2^(1+2^(2n+2))] and we can have n = 2^57
But we can do better than that … with n=2^57
[1,0,0,0,0,n]; [0,2,0,0,0,n]; [0,1,2,0,0,n]; [0,1,1,2,0,n];[0,1,1,1,n,0]; [0,1,1,1,0,2n];[0,1,1,0,2n,0];[0,1,0,2n,0,0];
[0,0,2n,0,0,0]
so we get to [0,0,2^58,0,0,0] and I think that following this through gives a higher bound than so far.
Comment by Mark Bennet — July 8, 2010 @ 8:37 pm |
These are based on an attempt to do a greedy right-first algorithm. It looks as though Terry may have done better than this (comment 40) – but I think the ideas for [1,1,1,1,1] might lead to a higher bound for the 6-case.
Comment by Mark Bennet — July 8, 2010 @ 9:06 pm |
Could one look at the simpler problems with less boxes and the same rules? Then try to find a function that from all possible distributions and then obtain an upper bound? For instance if there is one box we are done, we just have the number of coins in the box. For two the best we can do is twice the first box plus the second box. For three I think the upper bound is exponential.
Comment by Kristal Cantwell — July 8, 2010 @ 6:05 pm |
For three I think the best that can be done is [0,0,7]
Comment by DA — July 8, 2010 @ 6:23 pm |
It is looking like some combination of the methods in Comment thread 13 and Comment thread 7 is going to work: it seems that the 13 thread has generated far more than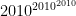 coins in the system, and the 7 thread provides a way to cut the coins back down in size. I think we’re in the home stretch here…
coins in the system, and the 7 thread provides a way to cut the coins back down in size. I think we’re in the home stretch here…
Comment by Terence Tao — July 8, 2010 @ 6:13 pm |
If we evaluate a coin at box 1 as 64 and a coin at box 2 as 32 etc then rule one preserves the value and rule two at most doubles it. So we need to apply rule 2 at least {2010^{2010} times log_2 2010 – log_2 127. This varies by a rounding error. The point is we can only apply rule 2 in slots one through four
so the total number of coins in the history of all states of the problem must total more than this enormous number in the first four slots. Based on this I now think this can be used to prove that the desired number cannot be reached.
Comment by Kristal Cantwell — July 8, 2010 @ 6:18 pm |
As others have observed, once you use the coin in box 1, it’s gone, and you are reduced to a 5-box problem.
So perhaps proceed by induction, adding a one-coin box to the left for each step of the induction?
Break it into three steps “Towers of Hanoi” style:
1) What do you do with boxes 2-5 before you use box 1?
2) Then what do you with box 1?
3) Then what do you do with boxes 2-5 after you use box 1?
(1) and (3) are a reduced problem on 5 boxes so maybe easier to analyze?
To get the biggest “bang for your buck” on step (2) — when you use that precious coin in box 1 — you want the contents of box 3 to be as large as possible and use your coin to pay for a swap. So I think an interesting question is how large you can make box 3 without using box 1… That is, how large can you make box 2 in the reduced “5-box problem”.
And similarly recursively. I think “how big can you make box 2 of the N-box case” is an interesting and relevant question…
Comment by Nemo — July 8, 2010 @ 6:18 pm |
Crud, I meant:
1) What do you do with boxes 2-6 before you use box 1?
2) Then what do you with box 1?
3) Then what do you do with boxes 2-6 after you use box 1?
Comment by Nemo — July 8, 2010 @ 6:19 pm |
If you’ve got enough stuff in box 6, it’s just a matter of littering a couple of coins in slots 3 and 4 to allow you to move the pile of coins from slot 6 to slot 4. Once you’ve done that, you can move as many coins as you like (since our target number is even) and then burn the rest away on idle shuffles.
Comment by Mike — July 8, 2010 @ 6:24 pm |
(1)![[N,M,0,0] \to [N-1, 1, 0, 2^{M+1}] \to [N-2,2^{M+1}, 0, 0 ]](https://s0.wp.com/latex.php?latex=%5BN%2CM%2C0%2C0%5D+%5Cto+%5BN-1%2C+1%2C+0%2C+2%5E%7BM%2B1%7D%5D+%5Cto+%5BN-2%2C2%5E%7BM%2B1%7D%2C+0%2C+0+%5D&bg=ffffff&fg=000000&s=0&c=20201002)
And we can get (2)![[0,0, 140, 0, 0 ,0]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C+140%2C+0%2C+0+%2C0%5D&bg=ffffff&fg=000000&s=0&c=20201002) as follows:
as follows:
By (1) combined with (2) we can get some number that is greater than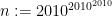 in the 4th spot
in the 4th spot
And swapping 5 with 6 enough times, we can adjust this number to have the value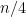 . Moving everything to the right will give us the desired result.
. Moving everything to the right will give us the desired result.
Comment by SM — July 8, 2010 @ 6:24 pm |
I think this is a correct solution!
I think it would be an interesting question to get some idea of what the largest number of coins one can have in the system is. The above argument gives something like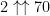 , where I am using the Knuth arrow notation. For comparison,
, where I am using the Knuth arrow notation. For comparison, 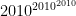 is about
is about 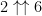 as discussed in comment thread 13.
as discussed in comment thread 13.
What upper bounds are possible? It seems that the argument in Comment 16 is giving a bound that is something like , which is huge. Can we get a bound of tower-exponential type (only two
, which is huge. Can we get a bound of tower-exponential type (only two 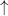 s?)
s?)
Comment by Terence Tao — July 8, 2010 @ 7:01 pm |
I also think this is a collect solution. Perhaps the approach used in 31 can give a tower exponential type bound. The idea would be to show that there is an exponential bound on the sum of all coins that
occupy box 4 throughout the history of the problem and then this would give the desired tower exponential bound.
Comment by Kristal Cantwell — July 8, 2010 @ 7:18 pm |
Another possibility for proving that we can’t get 2010^2010^2010 is a parity argument. Perhaps it’s impossible to get a number in that last bucket that is equivalent to 2010^2010^2010 mod q, for some q? This is a fleeting thought – so apologies if it’s patently wrong :).
Comment by Grant — July 8, 2010 @ 6:27 pm |
Well, you can get 0 in the last bucket in two moves:
[1, 1, 1, 1, 1, 1] –> (move 1) [1, 1, 1, 1, 0, 3] –> (move 2) [1, 1, 1, 0, 3, 0] so for this to work, q cannot be a factor of 2010^2010^2010…
Comment by mmailliw/william — July 8, 2010 @ 6:41 pm |
The coin in box 6 is completely useless. In fact, it’s a liability.
Comment by Nemo — July 8, 2010 @ 6:35 pm |
If the info in the last few replies of comment 13 are correct, then we can get well over 2010^2010^2010 in the last box. If anyone wants to check those replies for accuracy, that would be good.
What we now need is strategies for reducing the number of coins. Any ideas?
Comment by Aaron Hill — July 8, 2010 @ 6:54 pm |
You need to get the “big” number to box 4 so you can cut it down to size.
There is no mechanism for reducing a number in box 5 or 6.
Comment by Nemo — July 8, 2010 @ 6:56 pm |
what if we took the method from comment 13 and didn’t take it all the way to the end…
[7,1,1,1]
[7,1,0,3]
[6,1,0,2^3]
[5,1,0,2^2^3]
[1,1,0,2^2^2^2^2^2^3]
[1,0,2^2^2^2^2^2^3,0]
[0,2^2^2^2^2^2^3,0,0]
this dumps the big number in box 4
Comment by emily — July 8, 2010 @ 7:55 pm |
Maybe from [7, 1, 0, 3], don’t use up the whole 7? Just apply the “big rule” 6 times to get:
[1, 1, 0, 2^2^2^2^2^2^3]
(Have I got that right?)
If that’s big enough, do S4 and S3 to get
[0, 2^2^2^2^2^2^3, 0, 0]
Then use the ideas from thread 9 (apply S4 until the number is (1/4)*2010^2010^2010)
Then double it twice
Comment by Nemo — July 8, 2010 @ 7:02 pm |
One of the earlier comments showed 2010^2010^2010 < 2^2^2^2^4, this is definitely big enough to work.
Comment by mmailliw/william — July 8, 2010 @ 7:06 pm |
I think a way of doing this is given in comment 34: if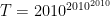 is the number we’re aiming for, then from
is the number we’re aiming for, then from ![[0,0,0,T/4,0,0]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C0%2CT%2F4%2C0%2C0%5D&bg=ffffff&fg=000000&s=0&c=20201002) one can get
one can get ![[0,0,0,0,0,T]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C0%2C0%2C0%2CT%5D&bg=ffffff&fg=000000&s=0&c=20201002) by two type 1 moves. Furthermore, one can get
by two type 1 moves. Furthermore, one can get ![[0,0,0,T/4,0,0]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C0%2CT%2F4%2C0%2C0%5D&bg=ffffff&fg=000000&s=0&c=20201002) if one can get
if one can get ![[0,0,0,X,0,0]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C0%2CX%2C0%2C0%5D&bg=ffffff&fg=000000&s=0&c=20201002) for any
for any  . And one can get
. And one can get ![[0,0,0,X,0,0]](https://s0.wp.com/latex.php?latex=%5B0%2C0%2C0%2CX%2C0%2C0%5D&bg=ffffff&fg=000000&s=0&c=20201002) for a massive
for a massive  by using the compound-compound move
by using the compound-compound move ![[a,b,0,0] \to [a-2, 2^{b+2}, 0, 0]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%2C0%2C0%5D+%5Cto+%5Ba-2%2C+2%5E%7Bb%2B2%7D%2C+0%2C+0%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Comment by Olof — July 8, 2010 @ 7:06 pm |
Special move,![[a,0,b]\rightarrow [0,0,b \times 2^a]](https://s0.wp.com/latex.php?latex=%5Ba%2C0%2Cb%5D%5Crightarrow+%5B0%2C0%2Cb+%5Ctimes+2%5Ea%5D&bg=ffffff&fg=000000&s=0&c=20201002)
Comment by DA — July 8, 2010 @ 7:03 pm |
To sum up the solution:
comment 34: [1,1,1,1,1,1] -> [0,0,140,0,0,0] is possible
using comment thread 13 we get [0,0,0,2^2^…^2,0,0] where the forth box is a tower of 140 floors, lets call this huge number x.
Using rule 1, we get [0,0,0,x-1,0,4], swapping box5 and box6 2k times: [0,0,0,x-2k-1,0,4]. Using rule 1 to move box4 to box6: [0,0,0,0,0,4*(x-2k)].
The remaining question is: can 2010^2010^2010 be written as 4*(x-2k)?
Clearly, by solving for k, we get k = x/2 – (2010^2010^2010)/8, which are integers, so the answer is affirmative.
Comment by Richárd Molnár-Szipai — July 8, 2010 @ 7:10 pm |
forgot to add, that k is positive of course
Comment by Richárd Molnár-Szipai — July 8, 2010 @ 7:12 pm |
Instead of using rule 1 after getting [0,0,0,X,0,0] for an absolutely huge X, use type 2 moves till it becomes the number one wants divided by 4, and then shift it along using type 1 moves.
Comment by Olof — July 8, 2010 @ 7:13 pm |
I wonder what the largest number you could make with N boxes is…
Comment by Nemo — July 8, 2010 @ 7:15 pm |
“The remaining question is: can 2010^2010^2010 be written as 4*(x-2k)?
Clearly, by solving for k, we get k = x/2 – (2010^2010^2010)/8, which are integers, so the answer is affirmative.”
This is actually not needed, since we can simple swap enought times to adjust the content of
enought times to adjust the content of 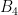 .
.
Comment by SM — July 8, 2010 @ 7:16 pm |
I think I can get somewhat larger number of coins in the system. We move as in Comment 34 until we reach
[0,1,19,0,0,0]
but then we use move (1) from Comment 34 nine times to end up with something like
(actually we get a little bit more than this, but we can burn off the excess if we wish), and then by Rule 2
which by many many applications of move (1) from comment 34 gives something like
and then by Michael’s move I get something like coins in the sixth box. That’s somewhere between
coins in the sixth box. That’s somewhere between 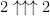 and
and 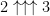 . I wonder if one can do much better than this…
. I wonder if one can do much better than this…
Comment by Terence Tao — July 8, 2010 @ 7:14 pm |
Following Michael idea:
Let F1 = […, N, P, …] -> […, N-1, P+2, …]
Let F2 = […, N, P,Q, …] -> […, N-1, Q,P, …]
Let F3 = […, N, 1, 1, …] -> […, N-1, 0, 7, …]
Let F4_k = […,N,0,Q,…] -> […,N-k,0,Q*2^k]
Let F5_k = […,N,0,0,…] -> […,N-k,0,2^(k+1)]
I think the following sequence of operation is working:
[0, 2, 0, 7, 1, 1] –(F3)–> [0, 2, 0, 6, 0, 7] –(F4_4)–> [0, 2, 0, 2, 0, 7*16] –(F2)–>
[0, 2, 0, 1, 112, 0] –(F2)–> [0, 1, 1, 0, 112, 0] –(F2)–> [0, 1, 0, 112, 0, 0] –(F5_108)–>
[0, 1, 0, 4, 0, 2^109] –(F2)–> [0, 1, 0, 3, 2^109, 0] –(F2)–> [0, 0, 3, 0, 2^109, 0] –(F2)–>
[0, 0, 2, 2^109, 0, 0] –(F5_(2^109-1))–> [0, 0, 2, 1, 0, 2^(2^109-1)] –(F2)–>
[0, 0, 2, 0,2^(2^109-1), 0] –(F2)–> [0, 0, 1, 2^(2^109-1), 0, 0] –(F5_(2^(2^109-1)-1)–>
[0, 0, 1, 1, 0, 2^(2^(2^109-1)-1)] –(F2)–> [0, 0, 1, 0, 2^(2^(2^109-1)-1), 0] –(F2)–>
[0, 0, 0, 2^(2^(2^109-1)-1), 0, 0]
Now 2^(2^(2^109-1)-1) > 2010^(2010^2010)
Applying F2 until the fourth number equal 0.5*2010^(2010^2010)+1
And applying F1 a number of time equal to 0.5*2010^(2010^2010) gives
[0,0,0,1,2010^(2010^2010),0] –(F2)–> [0,0,0,0,0,2010^(2010^2010)]
This solution requires a lof of F1 and F2 steps at the end, I wonder if we could use significantly less of them?
Comment by Mathieu Bouchard — July 8, 2010 @ 7:25 pm |
Oups the time to write this up I miss post 34
Comment by Mathieu Bouchard — July 8, 2010 @ 7:34 pm |
Our solution relies on the fact that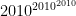 is even. Do we have a way of putting
is even. Do we have a way of putting  coins in the sixth box (with all other boxes empty?)
coins in the sixth box (with all other boxes empty?)
Regarding upper bounds, I think I can prove by induction on the number of boxes that B2 is always at most 3, and (when B1=1) B_2 is at most 1. Indeed, if we never touch B1, then we are effectively in the 5 box scenario, and B2 can never increase beyond 1. If we ever do touch B1, then just before we do so, by the induction hypothesis, either B2=1 (and so B3 is at most 1), or B2=0 (and so B3 is at most 3). Applying either Rule 1 or Rule 2 to B1 we conclude that B2 becomes at most 3, while B1 gets sent to zero. Any further moves can only serve to decrease B2.
Because of this, we can only apply Rule 1 or Rule 2 to B2 at most 3 times. This should help in giving a good upper bound on how many coins one can generate with six boxes.
Comment by Terence Tao — July 8, 2010 @ 8:07 pm |
To obtain an odd number: [0,0,0,N,0,0] -> [0,0,0,1,2N-2,0] -> [0,0,0,1,2N-3,2] -> [0,0,0,0,2,2N-3] -> [0,0,0,0,0,2N+1]
Comment by Mathieu Bouchard — July 8, 2010 @ 8:23 pm |
It’s interesting to see that we did need all 6 boxes, at least by the given approaches of [n, 0, 0] -> [0, 0, 2^n] and [A, n, 0, 0] -> [A-1, 0, 0, 2^2^n]. and so we need A=6.
and so we need A=6.
If I understood the notation correctly, we can get up to something like
So with 6 boxes, we could get A=7 which was enough… but with only 5 boxes, we’d be stuck at A=3 which would be have been too small. Good to know!
Comment by Jerzy Wieczorek — July 8, 2010 @ 8:09 pm |
For some suggestions on records, see 28 above.
I can get from [1,1,1,1,1] to [0,0,0,0,2^57]
And from [1,1,1,1,1,1] to [0,0,2^58,0,0,0] compared with the [0,0,140,0,0,0] required at comment 34 to solve the problem.
Comment by Mark Bennet — July 8, 2010 @ 8:45 pm |
I think the ideas at 40 might be combined with the ideas for the 5 case.
What is the highest n for which we can get from [1,1,1,1,1,1] to [0,1,n,?,?,?] ?
Greedy right-first algorithm looks at the 6th position rather than the third, and gets to [0,0,n,0,0,0] with a large n.
Comment by Mark Bennet — July 8, 2010 @ 9:10 pm |
If we do [1,1,1,1,1,1] becomes [0,3,0,3,0,3]
then [0,3,0,2,0,7]; [0,2,2,2,0,7];[0,2,2,1,0,14];[0,2,2,0,14,0];[0,2,1,14,0,0];[0,2,0,2^14,0,0]
then [0,1,2^14,0,0,0]
Comment by Mark Bennet — July 9, 2010 @ 8:33 am |
Now that the project is winding down a bit, I hope you can share your impressions of how it went, and what could be done to improve the process, over at the discussion thread:
Comment by Terence Tao — July 8, 2010 @ 10:38 pm |
[…] 关于Mini-polymath2 昨夜Terry Tao组织讨论2010年IMO的第五题。以mini-polymath的形式,整个过程可以说迅雷不及掩耳。我本来在想一些问题,大概仅仅2个半小时左右,这次讨论基本接近了尾声。这个计划结束时差不多已经凌晨三点。这里是这个活动的讨论贴。而这里是整个讨论过程。和去年的情形相比,今年效率大大提高。一方面参与者做好了准备,另一方面Tao的组织更有力。去年时候讨论了差不多三天。而且长时间处于无人组织的状态。另外,尽管有各种方法希望让后参与者更容易加入讨论,但是本次似乎所有主要参与者都是从那个头到尾一直在场的。还有一个问题就是,到目前为止似乎polymath的活动都是构造性的证明。我想,这是因为构造性的证明更容易总结。 […]
Pingback by 关于Mini-polymath2 « Xiaochuan Liu's Weblog — July 9, 2010 @ 1:39 am |
On Bounds
Let’s look at the functions which take a position with n in the first place and take this to the maximum possible number in the last place.
I think we have:
[n] gives the function f(n)=n
[n,0] gives f(n)=2n and [a,b] goes to b+2a
[n,0,0] goes to [n-1,2,0];[n-1,0,4];[n-2,4,0] … [0,2^n,0]; [0,0,2*2^n] so f(n)=2*2^n (n>0)
There is a reason for writing it this way.
[n,0,0,0] goes to [n-1,2,0,0] to [n-1,0,2^2,0] to [n-2,2^2,0,0] to [n-2,0,2^2^2,0] and (using ^ for an up-arrow cos I’m still getting LaTex sorted out) this looks like:
[n,0,0,0] goes to [0,2^^n,0,0] goes to [0,0,2^(2^^n),0] goes to [0,0,0,2*2^(2^^n)]
so that in the 4-place-case f(n) = 2*2^(2^^n)
And i think there are associated patterns for [a,b,c,d] etc
Similarly the five place case gives – if my arrow notation is correct f(n)=2*2^(2^^(2^^^n))
Six places is f(n) = 2*2^(2^^(2^^^(2^^^^n)))
Now we can take [2,0,0,0,0,0] to [1,1,1,1,1,2] which gives a greater value than [1,1,1,1,1,1]
So I reckon we have a bound of 2*2^(2^^(2^^^(2^^^^2))) and I think that exploring the patterns for [a], [a,b], [a,b,c] etc might give an exact maximum.
Comment by Mark Bennet — July 9, 2010 @ 12:13 pm |
Some special moves (which are the best=highest moves except when the numbers in the brackets are too small)
[a,b,0] goes to [a-1,2b,0] to … [0,b*2^a,0] to [0,0,2*b*2^a]
[a,b,c] goes to [a,0,c+2b]
goes to [a-1,c+2b,0]
goes to [0,0,2*(c+2b)*2^(a-1)]
(so this isn’t the best for [1,1,1] where it gives 2*2*(2^0)=4
[a,0,0] goes to [0,2^a,0]
[a,b,0,0] goes to [a,0,2^b,0] to [a-1,2^b,0,0] … to a tower of 2s “a” high with a “b” above it.
And here we start getting tied up in not having an adequate notation.
Comment by Mark Bennet — July 12, 2010 @ 12:57 pm |
If we generalize this to n boxes each one with one coin in it and the same rules and let f(n) be the maximum number of coins that we can get in the last box. What does f(n) look like? Is it primitive recursive?
Comment by Kristal Cantwell — July 9, 2010 @ 6:57 pm |
I think not, because we can take [1,1,1,1,1, … 1] to [0,3,1,1,1, … 1] and this gives a greater max value in the last place than
[0,3,0,0,0, … 0] for which see 47, which gives a result which I believe is not primitive recursive (subject to checking).
Comment by Mark Bennet — July 11, 2010 @ 9:38 pm |
So there are crude limits (with obvious notation)
[2,0,0,0, … 0] > [1,1,1,1 … 1] > [0,3,0,0, … 0]
Comment by Mark Bennet — July 11, 2010 @ 9:40 pm |
Special moves include
[n,0] to [0,2n]
[n,0,0] to [0,2^n,0]
[n,0,0,0] to [0,2^^n,0,0]
as at 47 above
The function f seems to go like this
[1] goes to 1
[1,1] goes to 3
[1,1,1] goes to 7
[1,1,1,1] goes to 28 (=2*14)
I reckon we have:
[1,1,1,1,1] to [1,1,0,0,7] to [1,0,2,0,7] to [1,0,1,0,14] to [1,0,0,14,0] (pull the 14 left rather than increasing it to 28)
to [0,2,0,14,0] to [0,1,14,0,0] to [0,1,0,2^14,0] to [0,0,2^14,0,0]
to [0,0,0,2^(2^14),0]
to [0,0,0,0,2*2^(2^14)]
so [1,1,1,1,1] goes to 2*2^(2^14)
Comment by Mark Bennet — July 12, 2010 @ 12:44 pm |
I think I can see the pattern here.
[1,1,1,1,1,1] goes to [1,0,0,2^14,0,0]
(nb the 7 is special at the tail – doesn’t quite fit the pattern)
(note 2^14 = 2^(2*7) which brings out the roles of 2 and 7 separately
and 2*2^(2^(2*7)) – two multiplications by 2, two powers
– the powers in between the multiplications in a chiastic structure)
[1,0,0,2^(2*7),0,0] goes to [0,2,0,2^(2*7),0,0]
The 2 in the second place is the source of two operations of the highest kind which appear in the answer.
The zeros at the end give space to repeat the power and multiplication operation in reverse.
This goes to [0,1,2^(2*7),0,0,0]
Which goes to [0,1,0,2^^(2^(2*7)),0,0]
Which goes to [0,0,2^^(2^(2*7)),0,0,0]
Which goes to [0,0,2^^(2^^(2^(2*7)),0,0]
… and eventually the result is 2*2^(2^^(2^^(2^(2*7)))
Comment by Mark Bennet — July 12, 2010 @ 4:42 pm |
Maybe there’s a a way to solve using conserved quantities?
Comment by John — July 11, 2010 @ 2:01 am |
Every extra place to the left adds an extra level of Knuth up-arrows to the maximum outcome of [n,0,0 … ,0] provided that n is at least 2 – this is the function of the second type of move (see 47 above).
BUT with [1,?,?, … ?] there can be advantages in using the first type of move more often, and the numbers in the left-hand places may not create the full value.
This creates constraints on how useful conserved quantities might be computed.
Comment by Mark Bennet — July 12, 2010 @ 10:02 pm |
[…] Problema Decorreu recentemente no The polymath blog e sob a organização de Terence Tao, a resolução conjunta do Problema 5 das Olimpíadas Internacionais de Matemática deste ano. Em vez do Problema 6, […]
Pingback by Problema 5 de IMO 2010 resolvido colaborativamente no projecto Mini-Polymath2 « problemas | teoremas — July 14, 2010 @ 10:22 pm |
There are various ways of getting a recursion formula going.
For n>1, let f(k,n,m) be the maximum value of d which can be obtained starting with
[n,m,0 … 0] (with k-2 zeros)
and ending with
[0,d,0 … 0]
Define f(1,n,0)=n (equivalent to [n] goes to [n])
Then (except perhaps for some marginal cases where m=1, which never arise staring with [n,0 … 0]
for k>1 f(k,n,0)=f(k,n-1,2)
(for n>0) f(k,n,m) = f(k,n-1,f(k-1,m,0))
and f(k,0,m) = f(k-1,m,0)
Comment by Mark Bennet — July 16, 2010 @ 5:16 pm |
I’ve been working on the biggest numbers you can get – based on what others have found.
I wonder – what is the most efficient solution – fewest number of moves?
Comment by Mark Bennet — July 16, 2010 @ 9:13 pm |
[…] you can see in the above link, Tao started a mini-polymath project about problem 5. So here you can see how a group of mathematicians worked together to solve that problem (and see the problem […]
Pingback by IMO 2010 « Absolutely useless — July 23, 2010 @ 8:34 pm |
[…] just opened the Mini-polymath2 project over at the polymath blog. I decided to use Q5 from the 2010 IMO in the end, rather than Q6, as […]
Pingback by Mini-polymath2 discussion thread « mathTHÍCHinTOÁNmyHỌCbrain — December 16, 2010 @ 12:43 pm |
[…] The format of the last year’s mini-polymath project seemed to work well, so I am inclined to simply repeat that format without much modification this time around, in order to collect a consistent set of data about these projects. Thus, the project will start at a pre-arranged time and date, with plenty of advance notice, and be run simultaneously on three different sites: a “research thread” over at the polymath blog for the problem solving process, a “discussion thread” over at this blog for any meta-discussion about the project, and a wiki page at the polymath wiki to record the progress already made at the research thread. (Incidentally, there is a current discussion at the wiki about the logo for that site; please feel free to chip in your opinion on the various proposed icons.) The project will follow the usual polymath rules (as summarised for instance in the 2010 mini-polymath thread). […]
Pingback by Mini-polymath 3: 2011 IMO question « What’s new — June 10, 2011 @ 12:49 am |
[…] and the spirit behind it. Personally, I had a blast trying to contribute (if only a tiny bit) to the 2010 event. Dang, I almost had comment […]
Pingback by Polymath project: social problem-solving | Civil Statistician — July 12, 2012 @ 6:31 pm |
[…] with Ackermann type bounds, though sometimes better bounds are available by trickier methods). Here is a discussion of an apparently simple problem from the 2010 IMO which generates beyond exponential rates of growth. You might want to try it first before reading […]
Pingback by What comes after exponents? – Math Solution — March 10, 2022 @ 1:22 pm |