This is a mock-up of what a research thread for a polymath project would look like. The thread would begin with a statement of the research problem, e.g.
Problem (Boundedness of the trilinear Hilbert transform). Show that the trilinear Hilbert transform
is bounded from
for some
(e.g.
and
).
Some discussion of the precise objective (are we aiming for an actual proof, or would we be happy with understanding why the problem is difficult?) would go here. [Note: while the above problem is an important open problem in harmonic analysis, I am not actually proposing to solve it by polymath here; it is only being used as an example for the purposes of this mock-up.]
A brief discussion of prior results would also be appropriate here, though an extended bibliography might be better placed on the wiki.
A reminder of the polymath rules might also be placed here, together with a link to the discussion thread for issues relating to exposition, strategy, and other meta-comments. The initiator of the project should also put some effort into laying down preliminary thoughts of the project as clearly as possible.
All threads in a polymath project would have a dedicated category; in this case, the category is mock-up.
Finally, one should put a list of moderators of the project, who would be able to respond to technical issues, such as fixing up a mangled comment. For this mock-up project, the moderators are:
- Terence Tao (tao@math.ucla.edu)
This is a test comment: “What would the trilinear Hilbert transform look like in terms of the Fourier transform ?”
?”
Note that comment numbering is automatic.
Comment by Terence Tao — July 26, 2009 @ 8:10 pm |
This is a test of comment nesting: a response to Comment #1. “It looks like the Fourier representation of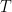 is of the form
is of the form
for some absolute constant C, where the integral is over the plane . Note that if one dropped the signum factor (and the constant C), this would be the formula for the Fourier transform for the pointwise product fgh, so perhaps it is good to think of
. Note that if one dropped the signum factor (and the constant C), this would be the formula for the Fourier transform for the pointwise product fgh, so perhaps it is good to think of 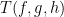 as a variant of the product fgh.”
as a variant of the product fgh.”
Note that responses are not automatically numbered.
Comment by Terence Tao — July 26, 2009 @ 8:18 pm |
Here is a second comment, not directly related to comment #1. “What if we try a dyadic model first, for instance replacing the real line by the p-adics for some small p, e.g. p=5? One could hope to then do some sort of induction on scales argument, perhaps using Bellman functions.”
Comment by Terence Tao — July 26, 2009 @ 8:19 pm |
[…] the ball rolling on this blog with some proposed rules for running a polymath, a mock-up of what a research thread and a discussion thread for a project would look like, two new proposals for the next polymath […]
Pingback by New polymath blog, and comment ratings « What’s new — July 28, 2009 @ 7:20 pm |