It’s probably time to refresh the previous thread for the “finding primes” project, and to summarise the current state of affairs.
The current goal is to find a deterministic way to locate a prime in an interval in time that breaks the “square root barrier” of
(or more precisely,
). Currently, we have two ways to reach that barrier:
- Assuming the Riemann hypothesis, the largest prime gap in
is of size
. So one can simply test consecutive numbers for primality until one gets a hit (using, say, the AKS algorithm, any number of size z can be tested for primality in time
.
- The second method is due to Odlyzko, and does not require the Riemann hypothesis. There is a contour integration formula that allows one to write the prime counting function
up to error
in terms of an integral involving the Riemann zeta function over an interval of length
, for any
. The latter integral can be computed to the required accuracy in time about
. With this and a binary search it is not difficult to locate an interval of width
that is guaranteed to contain a prime in time
. Optimising by choosing
and using a sieve (or by testing the elements for primality one by one), one can then locate that prime in time
.
Currently we have one promising approach to break the square root barrier, based on the polynomial method, but while individual components of this approach fall underneath the square root barrier, we have not yet been able to get the whole thing below (or even matching) the square root. I will sketch the approach (as far as I understand it) below; right now we are needing some shortcuts (e.g. FFT, fast matrix multiplication, that sort of thing) that can cut the run time further.
— The polynomial method —
The polynomial method begins with the following observation: in order to quickly find a prime in , it suffices to be able to quickly solve the prime decision problem: given a subinterval
of
, decide whether such an interval contains a prime or not. If one can solve this problem in, say,
time, then one can find a prime in this time also by binary search.
Actually, using Odlyzko’s method we can already narrow down to an interval of length with a lot of primes in it in
time, so we only need to break the square root barrier for the decision problem for intervals
of length
or less.
The decision problem is equivalent to determining whether the prime polynomial
(1)
is non-trivial or not, where ranges over primes in the interval
.
Now, the prime polynomial, as it stands, has a high complexity; the only obvious way to compute it is to enumerate all the primes from to
, which could take
time in the worst case. But we can improve matters by working modulo 2; note that as the coefficients of
are either 1 or 0, it suffices to decide whether
is non-trivial modulo 2.
The reason we do this is the observation that if is a natural number, then the number of solutions to the diophantine equation
with
is odd when n is prime, and usually even when n is composite. (There are some rare exceptions to this latter fact, when n contains square factors, but it seems likely that one can deal with these latter cases by Möbius inversion, exploiting the convergence of the sum
.) So, the prime polynomial f modulo 2 is morally equal to the variant polynomial
(2)
So a toy problem would be to decide whether (2) was non-zero modulo 2 or not in time or better.
The reason that (2) is more appealing than (1) is that the primes have disappeared from the problem. Instead, one is computing a sum over a fairly simple region bounded by two hyperbolae and two lines.
The point is now this: if vanishes modulo 2, then it also vanishes modulo
for any low-degree polynomial g (degree
or better), and more generally $\tilde f(x^n)$ vanishes modulo
. Conversely (if one is lucky), if
vanishes modulo
for sufficiently many
, then it should be that
vanishes. So this leads to the following strategy:
- Goal 1: Find a collection of
such that if
vanishes modulo
for all the pairs
, then
vanishes modulo 2.
- Goal 2: Find a way to decide whether
vanishes modulo
for all the required
in time
or better.
One way to achieve Goal 1 is to forget about , and choose the
so that the least common multiple of all the
(modulo 2) cannot divide
. Since
is basically a polynomial of degree
shifted by a monomial, one obvious way to proceed would be to pick more than
polynomials g. But then it looks unlikely that one can beat the square root barrier in Goal 2. Similarly if one varies n as well as g.
On the other hand, we have a partial result in Goal 2: for any fixed n and g, we can compute in time below the square root barrier, e.g. in time
. For instance, setting n=1 and
, we can compute
in this time. Unfortunately a single n,g is not nearly enough to solve Goal 2 yet, so we either need a further advance on Goal 1, or some very efficient way to test non-vanishing of
modulo (2,g) for many pairs (n,g) at a time (e.g. by an FFT type approach).
The partial result is based on the fact that has an arithmetic circuit complexity below the square root level, i.e. it can be expressed in terms of
(say) arithmetic operations. As such, for any low-degree g (say degree
),
can be computed in
time (using fast multiplication for mod g arithmetic if necessary).
Let’s sketch how the circuit complexity result works. Recall that (2) is a sum over the geometric region . Using the geometric series formula, one can convert this sum over
to a sum over what is basically the boundary of
. This boundary has
points, so this shows that
has an arithmetic circuit complexity of
already. But one can do better by using the Farey sequence to represent the discrete hyperbolae that bound
by line segments. The sum over each line segment is basically a quadratic sum of the form
for various coefficients
. It seems that one can factorise this sum as a matrix product and use ideas from the Strassen fast multiplication algorithm to give this a slightly better circuit complexity than the crude bound of
; see these notes; there may also be other approaches to computing this quickly (e.g. FFT).
Where we’re still stuck right now is scaling up this single case of Goal 2 to the more general case we need. Alternatively, we need to strengthen Goal 1 by cutting down substantially the number of pairs (n,g) we need to test…
[…] https://polymathprojects.org/2009/10/27/research-thread-v-determinstic-way-to-find-primes/ Possibly related posts: (automatically generated)You’ll Always Find Your Way Back Home New ClipSOME BEST WAYS 2 FIND NEW MUSICRavelry Finds ~ New Ways to Warm UpNo Way Home: The Rules […]
Pingback by New thread for deterministic way to find primes « Euclidean Ramsey Theory — October 28, 2009 @ 5:08 pm |
Regarding writing the prime generating function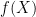 as a sum
as a sum  , where the
, where the  and
and 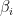 are sparse polynomials (say,
are sparse polynomials (say,  terms each): I had a conversation with a friend of mine this past weekend who is an expert on real algebraic geometry, and who was in town for the FOCS conference here at Georgia Tech. He said that in the
terms each): I had a conversation with a friend of mine this past weekend who is an expert on real algebraic geometry, and who was in town for the FOCS conference here at Georgia Tech. He said that in the ![R[x]](https://s0.wp.com/latex.php?latex=R%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) context (the
context (the 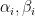 are polynomials with real coefficients) this problem is a well-studied in terms of trying to generalize Descarte’s Rule of Sign. If a single polynomial has only
are polynomials with real coefficients) this problem is a well-studied in terms of trying to generalize Descarte’s Rule of Sign. If a single polynomial has only  terms, Descarte’s rule implies that it can have at most
terms, Descarte’s rule implies that it can have at most  non-zero real roots, and apparently it is a studied open problem to extend this to a sum of products of two sparse polynomials like we have (but in
non-zero real roots, and apparently it is a studied open problem to extend this to a sum of products of two sparse polynomials like we have (but in ![R[x]](https://s0.wp.com/latex.php?latex=R%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) ). Perhaps there are some techniques that algebraic geometers have developed that would be useful in bounding the number of roots of our analogous polynomials in
). Perhaps there are some techniques that algebraic geometers have developed that would be useful in bounding the number of roots of our analogous polynomials in ![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) , or at least good conjectures. I didn’t get the chance to ask him what is known on this problem, but I will soon, and report back if I discover anything on it…
, or at least good conjectures. I didn’t get the chance to ask him what is known on this problem, but I will soon, and report back if I discover anything on it…
Incidentally, *he* initiated the discussion of this problem — not me — as it pertained to one of the FOCS talks on arithmetic circuit complexity.
Comment by Ernie Croot — October 28, 2009 @ 6:40 pm |
Oops… I meant to say “bounding the number of roots… among in
in ![F_2[x]/(2,g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%282%2Cg%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) ”.
”.
Comment by Ernie Croot — October 28, 2009 @ 7:01 pm |
It seems that the result on Descartes Rule uses special properties of the reals, and probably won’t extend to the complex (or finite field) setting. Here is the problem I asked my friend:
—-
Problem. Suppose that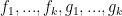 are all polynomials
are all polynomials![F_2[X]](https://s0.wp.com/latex.php?latex=F_2%5BX%5D&bg=ffffff&fg=000000&s=0&c=20201002) having
having  terms each. Let
terms each. Let 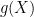 be an irreducible polynomial,
be an irreducible polynomial,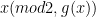 is at least
is at least  , say. Let
, say. Let
in
such that the order of
Show that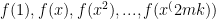 can’t all be
can’t all be  in
in ![F_2[X]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5BX%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) .
.
—-
And here was his response:
One remark about the problem. The fact that there exists any bound at all in terms of m and k in the real case has to do with the fact that we are bounding the number of real roots. Of course, no such bounds exist for complex roots — this makes me suspect that standard tools of algebraic geometry are probably not very useful in this context.
An exponential bound (in m as well as k) in the real case follows from Khovansky’s theory Pfaffian functions (you might want to look at the book “Fewnomials” by Khovansky).
But I do not think it can have applications in the finite field case where an exponential bound is probably obvious.
Comment by Ernie Croot — October 29, 2009 @ 10:19 pm |
I am not sure of this would help but would an approach on de randomizing a probabilistic algorithm for finding primes help? I attended midwest theory day and it seemed it may apply.
Click to access KvMS_full_manuscript.pdf
Comment by Joshua Herman — December 17, 2009 @ 4:01 am |
[…] then we had Polymath2 related to Tsirelson spaces in Banach space theory , an intensive Polymath4 devoted to deterministically finding primes that took place on a special polymathblog, a […]
Pingback by Polymath Reflections « Combinatorics and more — March 17, 2010 @ 7:34 pm |
I’ve discussed this problem briefly with Noam Elkies (on the train) and Hendrik Lenstra. Basically, if I understood correctly, Elkies thinks that the sort of combinatorial argument I gave for evaluating \sum_{n<=N} tau(n) quickly is essentially familiar to some experts (especially Lenstra), but Lenstra isn't sure that it isn't new as such.
—
This project seems to be dead now, or at least in a coma. What shall we do?
Comment by Harald — April 23, 2010 @ 8:15 am |
Hmm, good question. The project has certainly made definite progress, by identifying the right question (namely, breaking the square root barrier) and identifying a promising approach (to determine whether pi(b)-pi(a) is non-zero). And we are able to compute the mod 2 residue of this quantity pi(b)-pi(a) below the square root barrier, thanks to your observation and Ernie’s manipulations, and it is tempting to push this F_2 calculation up to F_2[x], but at that point we seem to require a miraculous identity which we do not currently possess.
One possibility is to pass the torch by writing up the parity calculation and some of its variants (as well as some of the counterexamples and other auxiliary results achieved along the way), and speculate on a future strategy. This of course is less satisfying than a full solution, but this is the nature of the game, of course…
Comment by Terence Tao — April 23, 2010 @ 4:52 pm |
Harald, sorry but I don’t check the polymath blog all that often (about once every week or two now). I think the problem of quickly evaluating sum of tau(n) is probably _not that_ new, in the sense that it is the -type of thing- known to experts… but I’m always hearing that from people about this or that idea I tell them, and then at the end of the day, it turns out to really be new… so, I would be skeptical of what Elkies says. In any case, that is only _one part_ of our overall algorithms for locating primes quickly — the totality of all our ideas are certainly new, and should probably be written up
Certainly, our ideas applied to the F_2[x] case (quickly evaluate the generating function) are fairly complex, and should be written up, even if we don’t produce a fast algorithm to find primes (I, however, am very bad at writing up ideas — it takes me _forever_ to write things up, and even then they are not easy for people to understand me. If we decide to write up the ideas, I would prefer not to be the person doing the actual writing… I will, however, help out by reading the draft, etc.)
…
I am still hopeful that we can make progress on the problem, and I have delayed working on it to focus on other things (principally writing up papers with Olof Sisask). I plan to work on it with some REU students this summer — actually maybe starting next week.
As I told you in an email, one extension of the ideas we have so far is to go to matrix rings, instead of F_2[x]: Basically, fix an n x n matrix A with entries in F_2[x], and then compute the prime generating function f at A — i.e. f(A) (mod 2, g(x)), for some low-degree g. Whereas it may take lots of evaluations in order to guarantee non-vanishing of f(x^j) (mod 2, g(x)), it may not take all that many when we use A — i.e. might only need f(A^j) (mod 2, g(x)) for a small number of j. I suppose one could diagonalize A (or put it into Jordan form) and convert the problem to polynomials, but perhaps if A has some special symmetry we can speed up the computations somewhat. That is one of the ideas I haven’t mentioned on the blog yet that I would like to explore.
Might there be some other structures we could use, besides matrix rings, where we can be guaranteed a huge speedup?
Comment by Ernie — April 27, 2010 @ 6:30 pm |
“other structures” e.g.: Use a Lie Algebra. I suppose the Lie bracket isn’t associative in general, so maybe that won’t work. What about endomorphism rings of elliptic curves?
Comment by Ernie — April 27, 2010 @ 7:06 pm |
These are interesting ideas, and would improve the “Goal 2” side of things.
In my opinion, though, the bigger stumbling block right now is “Goal 1”, which I don’t see how to make good progress on. A good toy problem is this: suppose we have a polynomial f of degree (say), and we want to know whether f mod 2 is non-zero or not. Let’s suppose that f has fairly small circuit complexity, e.g.
(say), and we want to know whether f mod 2 is non-zero or not. Let’s suppose that f has fairly small circuit complexity, e.g.  (to be very optimistic). This allows us to evaluate
(to be very optimistic). This allows us to evaluate 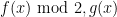 or
or  reasonably quickly for any fixed
reasonably quickly for any fixed 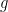 or
or  of low degree (e.g. degree at most
of low degree (e.g. degree at most  ). But I don’t see how to block the possibility that f is non-vanishing, but just happens to be divisible by all the g’s (and all the minimal polynomials of A’s) that we happen to test against, unless we use more than
). But I don’t see how to block the possibility that f is non-vanishing, but just happens to be divisible by all the g’s (and all the minimal polynomials of A’s) that we happen to test against, unless we use more than 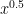 time or memory.
time or memory.
One amusing possibility here is to use P=BPP as a hypothesis. We figured out several months ago that P=BPP and a primality oracle were not sufficient, by themselves, to solve the problem; but P=BPP does allow for quick polynomial identity testing, which is basically the situation we’re in now…
Comment by Terence Tao — April 27, 2010 @ 8:46 pm |
Ah, my last comment was rubbish: we have a BPP algorithm to decide whether an interval contains a prime or not that runs in time , but to convert that algorithm into a P algorithm may well push one back over the square root barrier again.
, but to convert that algorithm into a P algorithm may well push one back over the square root barrier again.
Comment by Terence Tao — April 27, 2010 @ 9:17 pm |
First, let me say I don’t have time to comment much right now… maybe in a few days. But about Goal 1: I think if one could show that f(x^j) (mod 2, g(x)) doesn’t vanish for _some_ j up to n^(0.51), then one can produce a k x k matrix A so that some f(A^j) doesn’t vanish where j < n^(0.51)/k. So, you can get a reduction by a factor of k, but at the expense of having to work with matrices, instead of polynomials. Maybe something will come of that.
And about circuit complexity: The particular circuits we use aren't just of “low complexity'', but they are also of “low depth''. That might make a huge difference. As I have stated in comment 2. above, there might be a way to represent our prime generating function efficiently as a sum of products of sparse polynomials. If so, then maybe there are some algebraic-geometric tricks that can be used to get a handle on the non-vanishing (as in Saugata Basu's comments about Pfaffians).
Comment by Ernie — April 28, 2010 @ 4:22 pm |
Ernie,
I think you would be everybody a great service by writing up a quick, clear explanation of what you have (or don’t have) on F_2[x]. Let’s leave matrix rings for later. The details can then be written up by other people (= us), provided that we can bug you.
Comment by Harald — April 30, 2010 @ 12:24 pm |
There is a start on this at
http://michaelnielsen.org/polymath1/index.php?title=Polynomial_strategy
and see also
Click to access fast_strassen.pdf
I don’t know if things have advanced much beyond the stage when these notes were written.
Comment by Terence Tao — April 30, 2010 @ 3:52 pm |
Here’s one idea that occurred to me some time ago (in fact, it was inspired by this mathoverflow comment: http://mathoverflow.net/questions/3820/how-hard-is-it-to-compute-the-number-of-prime-factors-of-a-given-integer/10062#10062).
We now know how to compute the parity of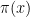 in time
in time 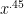 . We would be done (by binary search) if we could quickly find an interval
. We would be done (by binary search) if we could quickly find an interval ![[x,2x]](https://s0.wp.com/latex.php?latex=%5Bx%2C2x%5D&bg=ffffff&fg=000000&s=0&c=20201002) that contain an odd number of primes. Of course, this seems difficult.
that contain an odd number of primes. Of course, this seems difficult.
It seems, although I haven’t attempted to work this out, that we should be able to run a twisted version of the above algorithm to compute $\pi(x,a,q)$ also in time around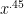 (with some reasonable dependence on $q$.) If this works, it then suffices to find some arithmetic progression with small modulus (say
(with some reasonable dependence on $q$.) If this works, it then suffices to find some arithmetic progression with small modulus (say 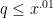 ) such that its intersection with the interval $[x,2x]$ contains an odd number of primes.
) such that its intersection with the interval $[x,2x]$ contains an odd number of primes.
It seems that this problem might be amenable to sieve theory. Specifically, it should suffice to show something like:
Now I'm not sure how to go about dealing with the sum on the left. One idea is to expand out the square and try to rewrite the terms involving using twisted divisor sum (as used in the algorithm above) and then hope that finite Fourier analysis and the large sieve could be used.
using twisted divisor sum (as used in the algorithm above) and then hope that finite Fourier analysis and the large sieve could be used.
Comment by Mark Lewko — April 28, 2010 @ 9:56 pm |
The sieve inequality I suggested above is nonsense since we should expect the summand on the left to be 1 or 0 about half the time. Although, it may still be useful to try to show that some AP with small modulus has an odd number of primes.
Comment by Mark Lewko — April 28, 2010 @ 11:34 pm |
Well, Ernie’s showed that the prime counting polynomial can be computed in subquadratic time if the gap between
can be computed in subquadratic time if the gap between 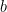 and
and  is say at most
is say at most 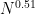 and g has degree at most
and g has degree at most 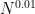 . In particular, setting
. In particular, setting 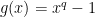 we get the residue counting functions
we get the residue counting functions 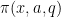 as coefficients.
as coefficients.
Unfortunately, probabilistic heuristics suggest that it is indeed possible to have a dense subset of (say)![[N, N+N^{0.51}]](https://s0.wp.com/latex.php?latex=%5BN%2C+N%2BN%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) which has an even number of elements in every residue class
which has an even number of elements in every residue class 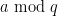 with
with  , since a random set will satisfy each of the
, since a random set will satisfy each of the  conditions with probability about 1/2, and there are
conditions with probability about 1/2, and there are 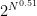 possibilities. Of course, the primes themselves only occupy an extremely small portion of the configuration space, and heuristically the above scenario should not actually occur for the prime counting function, but I have no idea how to formally prove this.
possibilities. Of course, the primes themselves only occupy an extremely small portion of the configuration space, and heuristically the above scenario should not actually occur for the prime counting function, but I have no idea how to formally prove this.
Comment by Terence Tao — April 30, 2010 @ 3:58 pm |
I have found 3 algorithms which determine primes without knowledge of previous
primes. Try these with an efficient program with which you are comfortable. I
use Fortran , a 1990 compiler, and run from DOS(the command promt). Very fast.
Comment by Tom Chenault — May 5, 2010 @ 7:56 pm |
Things seem to have ground to a halt. I do think that what we’ve got is interesting and deserves to be recorded, though; it should all be made into a short paper. Given that it will presumably be a collective work, wouldn’t it make sense for a third person (with the help of fourth or fifth persons…) to take care of some of the writing and the final editing?
I do sense Ernie has several interesting things to say that aren’t entirely clear to me yet, though. Anything cleanly stated coming from that direction would be deeply appreciated.
Comment by Harald Helfgott — June 10, 2010 @ 2:33 pm |
I think I’m inclined to agree that it may indeed be best to publish what we have. I wrote up a tentative outline of what the short paper could contain at
http://michaelnielsen.org/polymath1/index.php?title=Finding_primes#Outline_of_possible_paper
I think we could have an appendix doing Odlyzko’s method to localise pi(x) to accuracy O(x^{0.501}) in a bit more detail, as the references are not so well known. I was thinking of starting with the more elementary discussion of computing the parity of pi(b)-pi(a), and then moving to the more general discussion of the circuit complexity of sum_{a < p < b} t^p mod 2; strictly speaking the latter subsumes the former but I think for pedagogical reasons it would be good to discuss the former first (and this is how we found this approach historically).
As you know, I've got a number of other writing obligations to deal with in the near future, but I might be able to get a quick skeleton of such a paper in the near future. I was thinking to use Subversion to manage the task of editing the paper collectively; the previous approach of putting the raw LaTeX files on the wiki for Polymath1 was very clunky, and my experience so far with Subversion has been quite positive. It does require a small amount of software setup on each contributor's end, though.
Comment by Terence Tao — June 11, 2010 @ 12:25 am |
OK, I started writing an outline of a possible paper. Right now it has an introduction and several of the easier observations, and begins to touch the parity of pi(x) stuff, but I didn’t write anything on the more recent stuff on the prime polynomial mod 2, g. The LaTeX files can be found at
http://www2.xp-dev.com/sc/browse/86755/
If any of you are interested in working on the paper, if you can get an (free) xp-dev account and email me then I can add you to the list of editors on the project (though you’ll need to download subversion in order to check out a local copy of the paper and edit it on your own computer, see
). Or else we can improvise by email or something.
Comment by Terence Tao — June 12, 2010 @ 5:34 am |
I signed up for a Subversion account and sent you an email.
Comment by Kristal Cantwell — June 13, 2010 @ 7:38 pm |
I have not had the chance to meet with my REU students yet to discuss polymath4. That should happen this week (one of my students was away in Hungary, so we agreed not to meet until June). I did type up a short note explaining in a little more detail how the polynomial approach works; unfortunately, I cannot put it on my website just now, as my password expired (I need to go in to the dept. and change it from my office — I am away from my office right now). Too bad wordpress doesn’t allow file attachments. Let me instead try to write it out here… perhaps you can cut-and-paste-and-latex it:
\documentclass[12pt]{article}
\usepackage{amssymb}
\newcommand{\F}{{\mathbb F}}
\newcommand{\eps}{\varepsilon}
\title{The generating function of primes mod 2}
\begin{document}
\maketitle
\section{Introduction}
Fix a polynomial $f(x) \in \F_2[x]$ of degree $d$. We wish to compute
$$
\sum_{p \leq N} x^p \pmod{2,f(x)}
$$
quickly. We will explain how to do this (actually, a related problem — we confine to short intervals)
using at most $N^{1/2-\eps}$ or so bit operations.
\bigskip
Using the obvious generalization of our work for computing the parity of $\pi(x)$, it suffices to
show that we can compute
$$
\sum_{n \leq N} \tau(n) x^n \pmod{2,f(x)}
$$
in time $N^{1/2-\delta}$, for some $\delta > 0$. The larger $\delta > 0$ is in our algorithm, the larger
$\eps > 0$ will be.
\bigskip
Now what’s the idea? Well, let’s first think about the idea for the parity of $\pi(x)$: Recall that
what we essentially had to do was compute
\begin{equation} \label{squareroot_sum}
\sum_{n \leq \sqrt{N}} \lfloor N/n \rfloor
\end{equation}
substantially faster than the trivial algorithm, which takes time $N^{1/2 + o(1)}$. The key observation
was that we can compute the sum of fractional parts
$$
\sum_{x \leq n \leq x+q} \{N/x \},
$$
to within an error of $1/2$, for certain $x$ and $q$, very quickly — essentially time $O(1)$, which is faster by a factor of $q$
over the trivial algorithm. What allows us to do this is the fact that $N/n$ can be “linearized”, in the sense that
$$
|\{ N/n\} – \{N/x – at/q\}|\ <\ 1/2q,
$$
where $n = x+t$, and where $N/x^2 \sim a/q$.
So really all we need to compute is
$$
\sum_{x \leq n \leq x+q} \{N/x – at/q\}.
$$
(And, we need to fuss over certain exceptional cases.) And this is easily handled.
The analogue of the sum (\ref{squareroot_sum}) in the polynomial context is
\begin{equation} \label{insteadof}
\sum_{d \leq \sqrt{N}} \sum_{m \leq N/d} x^{dm}\ \pmod{2,f(x)}.
\end{equation}
Now of course we can use the geometric series formula (or other identities) to compute this in time
$N^{1/2+o(1)}$, so as in non-polynomial case that is the bound to beat.
Of course evaluating {\it that} sum quickly would be overkill as far as locating primes quickly.
Remember that upon using Odlyzko's algorithm, all we {\it really} need to be able to do is
to locate a prime quickly inside an interval $[N – N^{0.51}, N]$, since we can always localize
to some interval like that containing primes, using only $N^{0.49}$ operations. The sort of sum
we would need to evaluate in order to compute this “short interval'' generating function is
\begin{equation} \label{dN}
\sum_{d \leq \sqrt{N}} \sum_{(N – N^{0.51})/d \leq m \leq N/d} x^{dm} \pmod{2,f(x)},
\end{equation}
since it's not hard to imagine that computing sums such as this can be used to compute
$$
\sum_{N-N^{0.51} < n \leq N} \tau(n) x^n \pmod{2,f(x)}
$$
efficiently, which can be used to compute
$$
\sum_{N-N^{0.51} < p \leq N \atop p\ {\rm prime}} x^p \pmod{2,f(x)}
$$
efficiently.
And as a bonus, it turns out that upon confining ourselves to such short intervals (width $N^{0.51}$) we can beat
the trivial algorithm!
\bigskip
But now how do we do this — how do we beat the trivial bound of $N^{1/2+o(1)}$ for computing (\ref{dN})
efficiently (using the geometric series formula)? Well, the first thing to do is to split off the small $d$'s from the rest; that is,
we just compute
$$
\sum_{d \leq N^{1/2-\delta}} \sum_{(N-N^{0.51})/d \leq N/d} x^{dm} \pmod{2,f(x)}
$$
using the geometric series formula. So far, we have only consumed $N^{1/2-\delta+o(1)}$ operations
(OK, we lost a $N^{o(1)}$ — not important… we can just change $\delta$ to compensate). What remains, then, is
\begin{equation} \label{dm51}
\sum_{N^{1/2-\delta} < d \leq N^{1/2}} \sum_{(N-N^{0.51})/d \leq N/d} x^{dm} \pmod{2,f(x)}.
\end{equation}
Now of course we don't have a function like $\lfloor N/n \rfloor$ to play with that we can linearize. But we {\it can}
linearize {\it something} here: The first thing to note is that even if we just added every term together, and didn't
use the geometric series formula, we would get an upper bound of
$$
N^{1/2+o(1)} \cdot (N^{0.51}/N^{1/2-\delta})\ =\ N^{0.51+\delta+o(1)}
$$
for the running time. So, all we have to do is to improve this by a factor $N^{0.1 +\delta+o(1)}$, and we are in business.
Now we need an observation: Notice that if
$$
m/d\ =\ a/q + O(1/q^2),
$$
then
$$
|dm – (d-tq)(m+ta)|\ \ll\ t(d/q) + t^2 aq,
$$
which is quite a bit smaller than $dm$, provided that $q$ is much smaller than $d$, and provided that $t$ isn't
“too big''. So, if $dm$ were not too near the endpoints of the interval $[N-N^{0.51}, N]$, then we would expect that
for “$t$ not too big'', $(d-tq)(m+ta)$ is also in that interval.
What this allows us to do is to take the sum in (\ref{dm51}), and decompose it into a bunch of sums that look like
\begin{equation} \label{t0t1}
\sum_{t_0 \leq t \leq t_1} x^{(d-tq)(m+ta)} \pmod{2,f(x)}.
\end{equation}
Okay…. but how does this help? Well, that's where another trick comes in: It turns out that there is a way to convert
the problem of evaluating sums such as this one into a polynomial interpolation problem, and then one can apply
Strassen's algorithm. Once the dust has settled, one arrives at an algorithm to evaluate (\ref{t0t1}) in time at
most $(t_1 – t_0)^{0.9 + o(1)}$ — so, there is a saving by a factor $(t_1 – t_0)^{0.1}$, which is all we need.
What about this polynomial interpolation algorithm? Well, you can find it by going to the following note:
\begin{verbatim}
Click to access fast_strassen.pdf
\end{verbatim}
The vast majority of what makes my algorithm “technical and complex'' is that there are lots of little cases to
consider. e.g. What happens if $dm$ really is “near the endpoints''… how do we show that can't happen too often
to hurt us?
\end{document}
Comment by Ernie Croot — June 14, 2010 @ 5:16 am |
There is a small detail that should be corrected in the above: The fraction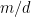 should come within
should come within  of the fraction
of the fraction 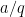 , where
, where 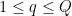 , and
, and 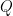 is to be carefully chosen — it will be some small power of
is to be carefully chosen — it will be some small power of  .
.
Comment by Ernie Croot — June 14, 2010 @ 2:43 pm |
I’ve converted this to a LaTeX file on the subversion repository at
http://www2.xp-dev.com/sc/browse/86755/
and also took the liberty of adding the fast Strassen file too for ease of reference.
Comment by Terence Tao — June 16, 2010 @ 1:10 am |
Terry, the note that I listed below is better — it took account of some other typos (and the 1/qQ issue). It is here:
http://www.math.gatech.edu/~ecroot/prime_generate.tex
Comment by Ernie Croot — June 16, 2010 @ 6:29 am |
[…] By kristalcantwell The results of Polymath4 are being written up. See this post. The latex files for the paper are […]
Pingback by Polymath4 « Euclidean Ramsey Theory — June 14, 2010 @ 6:12 pm |
I just had another thought on the “polynomial approach” to the problem: Instead of computing
I think it might be possible to ALSO give a quick-running algorithm for
(And then also replace polynomials rings with matrix rings, or other sorts of rings.)
The idea is that the “linearization steps'' in the algorithm for handling (1) should also apply to (2), though I have not checked this carefully yet — the “linearization'' is basically just Weyl-differencing, so it should work. In fact, perhaps one can replace the here with ANY BOUNDED DEGREE INTEGER POLYNOMIAL. Why would that be useful? Well, maybe it will help with Goal 1. Certainly, it would give a new way to approach it, because now we not only get to try to locate
here with ANY BOUNDED DEGREE INTEGER POLYNOMIAL. Why would that be useful? Well, maybe it will help with Goal 1. Certainly, it would give a new way to approach it, because now we not only get to try to locate  and
and  such that
such that  doesn't vanish mod
doesn't vanish mod 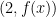 , but we also get to CHOOSE the polynomial in the exponent.
, but we also get to CHOOSE the polynomial in the exponent.
Perhaps one can go even further here, and replace polynomials in the exponent with sums of exponential functions like , say (I forget whether Weyl-differencing works with exponentials like that. I know sum-product estimates can be used to replace Weyl differencing in such a context, so maybe they can also be used here somehow…)
, say (I forget whether Weyl-differencing works with exponentials like that. I know sum-product estimates can be used to replace Weyl differencing in such a context, so maybe they can also be used here somehow…)
Ok, I sense nobody is seriously working on polynomath4 anymore… so I will save this for my REU students…
Comment by Ernie Croot — June 14, 2010 @ 11:05 pm |
I have put up a revised, pdf version of the “short note” above on the polynomial algorithm. To see this note, go here:
Click to access prime_generate.pdf
Comment by Ernie Croot — June 15, 2010 @ 11:11 pm |
Thanks! I will try to incorporate it into the short article that was already being drafted. If nothing else, it should serve as a good introduction to the REU project.
Comment by Terence Tao — June 16, 2010 @ 3:37 pm |
In the end, are we using Subversion, or are we improvising things over email. I would like to go on contributing, but, since I am traveling, installing new software seems non-trivial.
Comment by Harald — June 18, 2010 @ 5:39 pm |
Well, I’ve set up a Subversion repository for the project at
http://www2.xp-dev.com/sc/browse/86755/
so you can _download_ the files at any time whenever you have internet access, but to upload anything you either need to install the Subversion software, or email me with any modified files etc. Either way should work fine, though the former way would of course be more direct.
Comment by Terence Tao — June 18, 2010 @ 6:28 pm |
My first “.” should have been a “?”.
Comment by Harald — June 18, 2010 @ 5:44 pm |
We never got around to figuring out whether the method in Vinogradov’s exercises is original to Vinogradov, or whether it appeared before somewhere. (Vinogradov never gives references in his textbook, not even to his own work.) Has anybody got some sort of sense of what is the case here?
Comment by Harald Helfgott — July 17, 2010 @ 6:08 pm |
Hi there,
I did plot a graph for prime number against whole number on y axis. The graph was initially exponential and had became bit linear to the X-axis more and more as we had moved away from origin and parallel to X-axis.
There fore i am sure one point will cone after which we can’t come up with any prime number and that point would be the very intresting as well because at that point we can understand the spliting of a digit into two.
Thanking you
Shail
Comment by Shailendra — May 14, 2011 @ 9:10 am |
Спонсор ищет девушку
для настоящих
отношений, параметрыкретерии: от 18 до 20 лет рост
до 175 см. волосы светлые, модельное телосложение. личный помощник т.79262036777 Руслан
теги:
объявления знакомства
знакомства через интернет
Comment by Sponsers — May 18, 2011 @ 6:20 pm |
Познакомься на Love Znakomstva.tk – это сайт знакомств для тех, кто находится в поиске. Тех, кто ищет романтических отношений, дружеской привязанности или просто ни к чему не обязывающей болтовни. Зарегистрируйтесь, разместите свою фотографию и уже через несколько минут к вам в почту посыпятся десятки, а может и сотни писем с предложениями знакомиться, дружить или любить.
Comment by ZOJoseph — July 14, 2011 @ 2:09 am |
I have found a similar question that might help a bit? Let K be given and S the set of polynomials with positive coefficients. Find a polynomial of degree k which is irreducible in S adjoin [x] (which is fairly simplistic because you only need to show is that the coefficients add up to a prime number strictly greater than K and all coefficients must be 1 or greater). I don’t know if my proof is original but it certainly works. Suppose by way of contradiction, f(x) has degree K and all coefficients are 1 or greater where p is prime and f(1) = p > K. Suppose f(x) = g(x)h(x) where both g(x) and h(x) have positive coefficients. Then f(1) = g(1)h(1). But this is impossible unless [g(1) = 1 and h(1) = p] or [h(1) = 1 and g(1) = p]. Since the sum of coefficients of h(1) = 1 or p, we will assume not p and prove h(1) is invalid. Clearly if h(1) = 1, h(x) = x^m And we could divide through to get a new f(x) to which we repeat this process of dividing by h(x) until h(x) is 1 and f(x) is irreducible.
(So the easy way to come up with a polynomial is to have x^n + bx^(n-1) + 2x^(n-2) + 2^(n-3) … +2 where b is even and 1 + 2*(n-2) + b is prime and so f(1) = a prime and f(x) is irreducible under Eisenstein’s Criterion).
Now suppose we have for each K at least one corresponding f(x). How do we know that for some constant m f(m) is prime for some not-so-general and very-integery m AND m does not change for each f(x)? Find the least prime number, q, which is greater than any coefficients for any of the f(x) AND q must also be greater than K. The coefficients of the f(x) when put together side by side should form a number base q that is at least pseudoprime.
Examples: x^2 + 2x + 2. f(1) = 5. 122 base 5 is 37. Also 122 base 3 is 17.
x^2 + 4x + 2. 142 base 5 is 47. 142 base 7 is 79.
x^10 + 4x^9 + 2x^8 + 2x^7 + 2x^6 + 2x^5 + 2x^4 + 2x^3 + 2x^2 + 2x + 2. Which according to Wolfram Alpha when x = 11 the expression is prime. 35840804903.
To summarize this problem has already been solved in the S adjoin x world if by prime we mean irreducible. For any K, f(x) = x^K + 3 works (with Eisenstein’s). I was hoping something really cool would pop out of the polynomials.
I apologize as this response was a bit fuzzy (as my brain was not feeling perfect). I have not checked what kind of numbers one would want to plug in for f(x) = x^K + p to spit out numeric primes.
Comment by Brian Chen — December 23, 2011 @ 10:17 am |
Howdy all!
Just thought I’d let you know that I’ve proven Andrica’s Conjecture by re-examining the Sieve of Eratosthenes:
Click to access AndricaConjectureTrue.pdf
The proof shows that, at the n-th step of the sieve, the largest gap generated is at most $2 p_{n-1}$, from which Andrica follows. I call the state of elimination at the n-th step $\kappa_n$.
So, right off the bat, you can find a prime in $N^{1/2}$, even without the Riemann Hypothesis. (Note that this isn’t an asymptotic result, like $N^{0.525}$; it holds for all primes.)
However, I believe we can do a better search in practice. A naive generation of $\kappa_n$ up to $N$ requires $O(log N)$ computation and $O(N)$ storage. At that point, the density of primes is around
$M_n = \Pi_{i=1}^{n} \frac{p_i -1}{p_i} ~ \frac{1}{e^\gamma \log{p_n}}$
But a more sophisticated search would pre-calculate where in $\kappa_n$ $N$ lay and only keep around the requisite intervals, namely those that lie around a Biggest Resolution of $p_B = p_n$. Check out Theorems 2.8 and 2.9 for more details.
Btw, I’m firmly convinced Cramer’s Conjecture is true. I have developed a conditional proof that shows if Cramer’s Conjecture were true, then all the constellation infinity conjectures must be true simultaneously. Were Cramer true, then primes are packed incredibly tight and with much more regularity than we can currently show. The side effect of the conditional proof is that we could not only find _a_ prime after $N$ in log time, we could find the _exact next prime_ in log time.
I hope this helps you in your quest for deterministic prime finding!
Comment by Kim E Lumbard — December 23, 2011 @ 2:31 pm |
Is the algorithm given by Ribenboim in “Selling Primes” (My Numbers, My Friends), which constructs arbitrarily large proven primes, not sufficient?
Comment by Anonymous — May 14, 2013 @ 10:36 pm |
If you are referring to the algorithm in http://www.math.sunysb.edu/~moira/mat331-spr10/papers/1995%20RibenboimSelling%20Primes.pdf , the problem is that one needs to find (for a given prime p), an integer k for which 2kp+1 is prime. Such integers should exist in relative abundance, but there is no known rapid deterministic way of actually getting one’s hands on such a k other than by trying different k one at a time. (The section on “Feasibility of the algorithm” discusses this point.)
Comment by Terence Tao — May 14, 2013 @ 10:49 pm |
It seems (naively perhaps) that our parity result For the task of finding the parity of the number of primes in an interval gets quite close to the task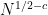 . The paper proposed a strategy of replacing “parity” by counting modulo other primes but
. The paper proposed a strategy of replacing “parity” by counting modulo other primes but
of finding a prime larger than N with running-time
it is also possible that one can use the parity result on its own. Once you find a single interval with an odd number of primes you can divide and conquer. I am not sure how hard it is to find a single interval with an odd number of primes. Here are a few related questions:
(1) Given n, what is the smallest t, such that for some one of the intervals [sn,(s+1)n] provably contains an odd number of primes?
one of the intervals [sn,(s+1)n] provably contains an odd number of primes?
(2) For the following sequences a_n is it provable that [a_n, 2a_n] contains an odd number of primes 2.1) infinitely many times, 2.2) half the times
a)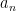 an arithmetic progression
an arithmetic progression
b)
c)
d)
So I am not sure if it is hopeless to demonstrate that there are infinitely many n’s so that there are odd number of n-digit primes
A sort of vaguely related question is if the variant of the zeta function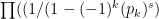 where
where  is the kth prime was considered.
is the kth prime was considered.
Comment by Gil Kalai — January 28, 2015 @ 3:47 pm |
Number Theory_Proofs_about strong (binary) Goldbach Conjecture & Riemann Hypothesis, Gaps of primes & quasi primes (semi primes) , perfect numbers etc.
Is Polymath Project interesting in Scientific Publication ?
(Let’s say: Published by Polymath Project, VSD (GR))
(at ArXiv.org, about 26 word pages, without figures, font Times New Roman 12, in greek language. I haven’t translated in english the document yet ).
Thank you in advance.
Proofs at “A new polymath proposal (related to the Riemann Hypothesis) over Tao’s blog”
Proofs at “(Research thread V) Deterministic way to find primes”
Proofs at “Polymath proposal: bounded gaps between primes”
(since 10/10/2024…)
1. The Riemann Hypothesis is TRUE (Proof).
(Mathematical society has already proved it. I simply combined a formula with Riemann harmonics and the Riemann converter. My contribution to the RH problem is no greater than 10%, maybe less.)
2. The strong (binary) Goldbach conjecture is TRUE (Proof)
As re-expressed by Euler, an equivalent form of this conjecture (called the “strong” or “binary” Goldbach conjecture) asserts that “all positive even integers ≥4 can be expressed as the sum of two primes.”
3. The “strongly weak” Levy’s Conjecture is TRUE (Proof)
“all odd numbers ≥7 are the sum of a prime plus twice a prime.” “an odd number can be written as a sum p+2q with p,q primes”
4. de Polignac’s Conjecture or Twin prime conjecture is TRUE (Proof)
Twin prime conjecture: “Every even number is the difference of two consecutive primes in infinitely many ways (Dickson 2005, p. 424). If true, taking the difference 2, this conjecture implies that there are infinitely many twin primes (Ball and Coxeter 1987).”
5. a) There is NOT odd perfect number (Proof)
b) Infinite number of Mersenne quasi primes or Mersenne primes. (Proof)
6. i) Brocard’s Conjecture is TRUE (Proof)
“π(p(n+1)^2) – π(p(n)^2) ≥ 4 , p(n), p(n+1) primes”
ii) Legendre Conjecture is TRUE (Proof)
“for every n there exists a prime p between n^2 and (n+1)^2”
iii) Waring’s Prime Number Conjecture is TRUE (Proof):
“every odd integer is a prime or the sum of three primes.”
7. a) square free Euclid Numbers Conjecture is TRUE (Proof),
En=p#n+1=p1p2p3…pn + 1
b) Infinite number of Fermat quasi primes or primes (Proof)
c) Infinite quasi primes or prime numbers of form N^2+1 (Proof)
d) Infinite number of Sophie Germain primes (Proof)
e) Infinite number of Fibonacci quasi primes or primes (Proof)
f) If GCD(a,d)=1 a,d:coprimes , n≥1 integer => a+nd=p, p prime
g) Upper limit at Bertrand’s Postulate (Proof)
8. Primes – quasi-primes Reciprocals Conjecture:
p: prime or quasi-prime, L: period of 1/p, Reciprocal’s Digital Root=9
m=10^x , x= L-log9-logp , x>0
Conclusion:
I think, we can not distinguish prime numbers & quasi numbers (semiprimes). Thus, integer factoring is a NP-complete problem. Thank God!
Feedback is desirable!
VSD, Chemical Engineer, MBA, MBIT
(Greece – GR)
Comment by Anonymous — November 23, 2024 @ 11:53 am |