Here is a proposal for a polymath project:
Problem. Find a deterministic algorithm which, when given an integer k, is guaranteed to find a prime of at least k digits in length of time polynomial in k. You may assume as many standard conjectures in number theory (e.g. the generalised Riemann hypothesis) as necessary, but avoid powerful conjectures in complexity theory (e.g. P=BPP) if possible.
The point here is that we have no explicit formulae which (even at a conjectural level) can quickly generate large prime numbers. On the other hand, given any specific large number n, we can test it for primality in a deterministic manner in a time polynomial in the number of digits (by the AKS primality test). This leads to a probabilistic algorithm to quickly find k-digit primes: simply select k-digit numbers at random, and test each one in turn for primality. From the prime number theorem, one is highly likely to eventually hit on a prime after about O(k) guesses, leading to a polynomial time algorithm. However, there appears to be no obvious way to derandomise this algorithm.
Now, given a sufficiently strong pseudo-random number generator – one which was computationally indistinguishable from a genuinely random number generator – one could derandomise this algorithm (or indeed, any algorithm) by substituting the random number generator with the pseudo-random one. So, given sufficiently strong conjectures in complexity theory (I don’t think P=BPP is quite sufficient, but there are stronger hypotheses than this which would work), one could solve the problem.
Cramer conjectured that the largest gap between primes in [N,2N] is of size . Assuming this conjecture, then the claim is easy: start at, say,
, and increment by 1 until one finds a prime, which will happen after
steps. But the only real justification for Cramer’s conjecture is that the primes behave “randomly”. Could there be another route to solving this problem which uses a more central conjecture in number theory, such as GRH? (Note that GRH only seems to give an upper bound of
or so on the largest prime gap.)
My guess is that it will be very unlikely that a polymath will be able to solve this problem unconditionally, but it might be reasonable to hope that it could map out a plausible strategy which would need to rely on a number of not too unreasonable or artificial number-theoretic claims (and perhaps some mild complexity-theory claims as well).
Note: this is only a proposal for a polymath, and is not yet a fully fledged polymath project. Thus, comments should be focused on such issues as the feasibility of the problem and its suitability for the next polymath experiment, rather than actually trying to solve the problem right now. [Update, Jul 28: It looks like this caution has become obsolete; the project is now moving forward, though it is not yet designated an official polymath project. However, because we have not yet fully assembled all the components and participants of the project, it is premature to start flooding this thread with a huge number of ideas and comments yet. If you have an immediate and solidly grounded thought which would be of clear interest to other participants, you are welcome to share it here; but please refrain from working too hard on the problem or filling this thread with overly speculative or diverting posts for now, until we have gotten the rest of the project in place.]
See also the discussion thread for this proposal, which will also contain some expository summaries of the comments below, as well as the wiki page for this proposal, which will summarise partial results, relevant terminology and literature, and other resources of interest.
This is certainly an interesting problem, from a pure mathematician’s perspective anyway. (From a practical point of view, one would be happy with a randomized algorithm, but there’s no denying that to find a deterministic algorithm for such a basic problem would be a great achievement if it could be done.)
My first reaction to the question of whether it is feasible was that it seems to be the kind of problem where what is needed is a clever idea that comes seemingly out of the blue and essentially cracks the problem in one go. Or alternatively, it might need a massive advance in number theory, such as a proof of Cramer’s conjecture. But on further reflection, I can see that there might be other avenues to explore, such as a clever use of GRH to show that there is some set (not necessarily an interval) that must contain a prime. Even so, it feels to me as though this project might not last all that long before it was time to give up. But you’ve probably thought about it a lot harder and may see a number of interesting angles that I don’t expect, so this thought is not necessarily to be taken all that seriously. And perhaps the magic of Polymath would lead to unexpected lines of thought — in a sense, that is the whole point of doing things collectively.
This raises another issue. It might be that a Polymath project dwindles after a while, but then someone has an idea that suddenly makes it seem feasible again. In such cases, it might be good to have a list that people could subscribe to, where a moderator for a given project could, at his or her discretion, decide to email everyone on the list to tell them that there was a potentially important comment.
Comment by gowers — July 27, 2009 @ 1:47 pm |
Dear Tim,
Actually I’ve only thought about this problem since Bremen, where I mentioned it in my talk. As I mentioned in my post, I doubt a polymath would be able to solve it unconditionally, but perhaps some partial result could be made – for instance, one could replace the primes by some other similarly dense set (almost primes is an obvious candidate, as sieve theory techniques become available, though the resolution of sieves seems too coarse still). Another question is whether this derandomisation result would be implied by P=BPP; I mistakenly thought this to be the case back in Bremen, but realised afterwards that P and BPP refer to decision problems rather than to search problems, and so I was not able to make the argument work properly.
Regarding notification: we already have RSS feeds that kind of do this job already. For instance, if one has a feed aggregator such as Google Reader, one can subscribe to the comments of a given post by following the appropriate link (in the case of this post, it is https://polymathprojects.wordpress.com/2009/07/27/proposal-deterministic-way-to-find-primes/feed/ ).
Comment by Terence Tao — July 27, 2009 @ 2:47 pm |
Amusingly, the problem occurred to me too when you were giving your talk (not as a polymath project, but just as an interesting question).
I’m trying to think whether there’s a way of using P=BPP to find primes with k digits. I find it easy to make stupid mistakes, so here’s an argument that could be rubbish but feels quite reasonable to me at the time of writing. I’d like to show that there’s a randomized algorithm for finding primes by solving decision problems. So here is the problem that this randomized algorithm solves.
GIVEN: an interval of integers that contains a reasonable number of primes and is partitioned into two subintervals.
WANTED: one of the subintervals that still contains a reasonable number of primes.
The randomized algorithm for solving this would be to take random samples from one of the subintervals in order to estimate, with a high probability of accuracy, the density of primes in that subinterval. That enables us to choose a good subinterval with only a small probability of failure, and in that way one should, it seems to me, be able to get more and more digits of a prime. (Late on in the procedure, one would be doing more random samples than there are points in the interval, because one would have to check all points in the interval. But by that time the size of the interval would be logarithmic.)
So then the hope would be that by derandomizing one could get a deterministic algorithm for working out more and more digits. There are clearly details to check there, but it feels as though it could work. Or maybe you’ve tried it and the numbers don’t obviously work out.
I thought of RSS feeds, but what I was wondering about was a way of notifying people not necessarily every time there was a new comment, but only when the comment was of a kind that could potentially get a project going again when it appeared to have stalled. But perhaps the frequency of comments would be small enough that RSS feeds would be a perfectly good way of doing this.
Comment by gowers — July 27, 2009 @ 3:52 pm |
I haven’t thought about the problem too deeply yet, but the problem I recall facing was that BPP requires a significant gap between the success rate when the answer is “yes” and when the answer is “no” (this is the “B” in “BPP”), whereas the transition between “lots of primes in an interval” and “few primes in an interval” is too vague to create such a sharp separation. (This is in contrast to, say, polynomial identity testing over finite fields, where there is a big gap between the identity holding all the time, and only holding a small fraction of the time.) But if there was a “locally testable” way of finding whether there were primes in an interval, then we might begin to be in business…
Regarding RSS, perhaps RSS for the discussion thread alone (rather than the research thread) may suffice. This, by the way, is one potential advantage of having a centralised location for polymath activity; anyone who follows this blog on a regular basis will learn about an exciting revival in a previously dormant project, without having to follow that project explicitly.
Comment by Terence Tao — July 27, 2009 @ 5:04 pm |
I’d be slightly (but possibly wrongly) surprised if that was the problem, simply because BPP could certainly detect a difference in density of say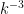 , where
, where  is the number of digits of
is the number of digits of  . You’d just have to take significantly more than
. You’d just have to take significantly more than 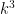 samples for the difference to show up. And a product of factors of size around
samples for the difference to show up. And a product of factors of size around 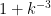 would not get big after
would not get big after  steps.
steps.
Comment by gowers — July 27, 2009 @ 6:39 pm |
I think that this would be a problem and is a well-known one with “semantically”-defined complexity classes. The problem is that in order to use the P=BPP assumption you must first convert the approximation problem into a decision problem which has a randomized algorithm with probability of correctness at least 1/2+1/poly. While you can randomly in polynomial time estimate the number of primes in the interval [x,y] to within 1/poly (and this precision should suffice for a binary search), in order to de-randomize it using the P=BPP assumption you will have to transform it to some boolean query such as: “is the number of primes in the interval [x,y] at least t” which is not (as far as we know) in BPP since a randomized algorithm will not have correctness probability >1/2+1/poly for t that is very close to the right number.
Comment by Noam — July 28, 2009 @ 11:56 am |
Ah — what I was hoping for was an argument like this. We know that the density in at least one interval is at least . So we use a randomized algorithm to identify an interval with density at least
. So we use a randomized algorithm to identify an interval with density at least 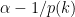 . We can design this so that if the density is less than
. We can design this so that if the density is less than  then with high probability it will not choose that interval, and if it is at least
then with high probability it will not choose that interval, and if it is at least  then it will choose the interval. And if the density is between
then it will choose the interval. And if the density is between  and
and  then we don’t care which it chooses. But it seems from what you say that a slightly stronger assumption that P=BPP is needed to derandomize this procedure. (Here is where I reveal my ignorance: it seems to me that one could just use pseudorandom bits rather than random bits in performing the above procedure. All that could go wrong is that either the density is less than
then we don’t care which it chooses. But it seems from what you say that a slightly stronger assumption that P=BPP is needed to derandomize this procedure. (Here is where I reveal my ignorance: it seems to me that one could just use pseudorandom bits rather than random bits in performing the above procedure. All that could go wrong is that either the density is less than  and it accepts the interval, or the density is at least
and it accepts the interval, or the density is at least  and it declines it. But in both cases it is behaving differently from a truly random source.)
and it declines it. But in both cases it is behaving differently from a truly random source.)
Comment by gowers — July 28, 2009 @ 1:11 pm |
yes, pseudorandom bits would suffice for this to work. However the existence of a PRG is a stronger assumption than P=BPP and even stronger than the condition that you are looking for (which is sometimes called P=promise-BPP which means that randomized algorithms that sometimes do not have a gap can still be de-randomized as long as the deterministic algorithm is allowed to give an arbitrary answer when the gap is too small.)
Comment by algorithmicgametheory — July 28, 2009 @ 2:09 pm |
Ah — now we’ve got to the heart of what I didn’t know. I had lazily thought that because the heuristic reason for expecting P to equal BPP is that pseudorandom generators probably exist, the two were equivalent.
Comment by gowers — July 28, 2009 @ 2:43 pm |
It looks that both the number theory version and the computational complexity problem are interesting and probably very difficult. Probably this is a problem I would first ask some experts in analytic number theory for some appropriate NT conjectures and some real expert in complexity. Probably there are known cases of search problems which admit randomized polynomial algorithm where even assuming P=BPP (namely that randomization does not help for decision problems) you cannot derandomize the algorithm. (But maybe this is nonsense Avi Wigderson is a person to ask.)
Now here is a silly question: If I grant you a polynomial time algorithm for factoring does this gives you a polynomial time deterministic algorithm for coming with a k digit prime number?
Comment by Gil Kalai — July 27, 2009 @ 6:13 pm |
Hmm, I like this question also; it relates to the proposal of finding almost primes rather than finding primes. So it looks like while the original problem is very hard, there are a large number of ways to “cheat” and make the problem easier. Hopefully there is some variant of the problem which lies in the interesting region between impossibly difficult and utterly trivial…
Hopefully, some experts in NT and/or complexity theory will chime in soon… but certainly the next time I bump into Avi or anyone other expert, I might ask this question (I actually learned about this problem from Avi, incidentally).
Comment by Terence Tao — July 27, 2009 @ 6:29 pm |
It is tempting to try to mix-and-match various number theory and complexity theory hypotheses to get the result. I would love to have a result that needed both GRH and P!=NP to prove!
Just as a joke, here is one potential approach to an unconditional resolution of the problem:
There are two cases, P=NP, or P!=NP.
1. If P=NP, then presumably the problem of finding a k-digit prime is close enough to being in NP, that it should be in P also (modulo the usual issue about decision problem versus search problem). Done!
2. If P != NP, then one should be able to use an NP-complete problem to generate some sort of really strong pseudorandom number generator (as in Wigderson’s ICM lecture), which could then be used to derandomise the prime search problem. Done!
This is no doubt too silly to actually work, but it would be amusing to have a proof along these lines…
Comment by Terence Tao — July 27, 2009 @ 7:15 pm |
Two small comments about that. If P=NP then finding a k-digit prime is certainly in P, since one can simply get the computer to say yes if there’s a k-digit prime with first digit 1 (a problem in NP), and then 2,3, etc. And then one can move on to the second digit, and so on.
Also, the assertion that there is a pseudorandom generator is generally regarded as stronger than P not equalling NP. You need a 1-way function for it. Often, such results are proved on the assumption that the discrete logarithm problem is hard, but that’s a stronger assumption because discrete log is (probably) not NP complete.
The only way I can think of of rescuing the approach is to find k-digit primes by showing that if you can’t, then you can build a pseudorandom generator. Not sure how that would go though!
Comment by gowers — July 27, 2009 @ 7:45 pm |
Ah, I knew it was too good to be true. But now I’ve learned something about computational complexity, which is great. And now we can assume P!=NP for free. Progress!
A world in which the answer to the above problem is “No” would be very strange – every large constructible integer would necessarily be composite (note that the set of all numbers constructible in poly(k) steps from an algorithm of length O(1) can be built (and tested for primality) in polynomial time). It could well be that one could use this strangeness to do something interesting (particularly if, as Gil suggests, we assume that factoring is in P, at which point in order for the answer to be “No”, all large constructible integers are not only composite, but must be smooth). It sounds from what you said that we might also be able to assume that discrete log is in P also. I’m not sure what we could do with all that, but it might well lead to some assertion that cryptographers widely believe to be false, and then that would be a reasonable “solution” to the problem.
Comment by Terence Tao — July 27, 2009 @ 7:53 pm |
Don’t all large constructable numbers have to not only be composite but also surrounded by large gaps free of prime numbers?
Comment by Kristal Cantwell — July 28, 2009 @ 11:22 pm |
I suggest to look at the question under the assumption that we have an oracle (or a subroutine)that can factor numbers (at a unit step). (We can also ask the problem under the assumption that factoring is in P but I am not sure this is equivalent to what I asked.) Since factoring looks so much harder than primality one can wonder if factoring will help in this problem: something like: you want to have a prime number with k digits? start looking one after the other in numbers with k^3 digitsfactor them all and you are guaranteed to find a prime factor with k digits.
It is sort of a nice game: we will give you strong oracles or strong unreasonable assumptions in computational complexity just that you can believe slighly less extreme conjecture in analytic number theory, all for the purpose of derandomization.
I think this is refer to as Pig-can-fly questions in CC but I am not sure if this is the right notion and what is its origin.
Comment by Gil Kalai — July 30, 2009 @ 12:33 pm |
That sounds quite plausible. After all, the Erdos-Kac theorem already tells us reasonably accurately how the number of prime factors of a random large number near n is distributed. How large an interval do we have to take around n for the theorem to hold? (I am not sufficiently well up on the proof to know the answer to this, but I’m sure there are people here who do.) And if it holds, we would expect not only that a typical number has about loglogn factors, but also that some of these factors are of size roughly . Does that follow from their argument?
. Does that follow from their argument?
The weak link in that is that one might have to look at far too many numbers near n for it to work. But somehow it feels as though proving that at least some number in a short interval near n has a typical arrangement of prime factors ought to be a lot easier than proving that at least some number in a short interval near n is prime. This could be quite an interesting problem in itself, though I suppose there’s a good chance that it is either known, or else that despite what I said above, it is in fact just as hard as Cramer’s conjecture.
If this idea has anything going for it, then a great first step would be for somebody to put on the wiki a sketch of a proof of Erdos-Kac, or at least of Turan’s simpler argument that the variance of the number of prime factors is about loglogn (if I remember correctly). Talking of which, Michael Nielsen and I have written a few short wiki pages about complexity classes. Any additions would be welcome.
Comment by gowers — July 30, 2009 @ 1:48 pm |
I can try to put some things on the Wiki about Erdös-Kàc during the week-end. I’m not sure what to expect from it, because the only knowledge about primes that goes in the proof even of the strongest version amounts to the standard zero-free region for the Riemann zeta function.
Comment by Emmanuel Kowalski — July 30, 2009 @ 3:27 pm |
This types of questions/results are described by the phrase “If pigs could whistle then horses could fly” and apparently the use in computational complexity goes back to Mike Sipser who wrote me:
“When I taught advanced complexity theory in the 1980s, I used that phrase to describe theorems likeIf there is a sparse NP-complete set then P=NP, and If some NP-complete set has poly size circuits then PH = \Sigma_2.
I may have heard it myself somewhere before, not sure.
It appeared I think in my complexity lecture notes from that period, but not to my memory in any of my papers. But lots of good people took my class, so maybe one of them wrote something with it? (My 1986 class was especially remarkable: Steven Rudich,Russell Impagliazzo, Noam Nisan, Ronitt Rubinfeld,Moni Naor, Lance Fortnow, John Rompel, Lisa Hellerstein, Sampath Kannan, Rajeev Motwani, Roman Smolensky,
Danny Soroker, Valerie King, Mark Gross,and others I’m forgetting were in it)”
We somehow add also number theory conjectures into it, so we are looking at something like “If pigs could whistle assuming RH then horses could fly assuming Cramer’s conjecture.”
(Added Oct 2015) Rubinfeld’s reflections on this mythological class are recorded here: https://www.dropbox.com/s/abmq168qoqriztv/2014-10-27%2000.38.04.mp4?dl=0
Comment by Gil Kalai — July 30, 2009 @ 3:37 pm |
A thought that ended up going round in circles: I was wondering if we could reduce to the case where factoring was in P, by assuming factoring was hard and obtaining a pseudorandom number generator. It was tempting to just run RSA iteratively to generate this… but realised that for RSA to work, one first has to generate large primes. Argh! [Note: the same argument also renders discrete log useless, since we can’t find large primes to run discrete log on.]
Comment by Terence Tao — July 27, 2009 @ 8:09 pm |
I think that there might be a complexity-theory de-randomization angle of attack here.
One-way functions are not needed for the PRGs here, and a sufficient assumption is that DTIME(2^n) does not have sub-exponential size circuits (this is the Impagliazzo-Wigderson PRG). There may be several strategies of getting a PRG-like entity for this problem with no (or with less) complexity assumptions either by getting rid of the “non-uniformity” replacing it by diagonalization (e.g. something like http://www.math.ias.edu/~avi/PUBLICATIONS/MYPAPERS/GW02/gw02.pdf ) or by considering a weaker set of tests.
A partial result in this direction (from a de-randomization point of view) would be to reduce the number of random bits needed for finding an n-bit prime. (O(n^2) would be trivial since you expect to find a prime after O(n) random probes, getting to O(n) bits is a nice exercise, and o(n) would be interesting, I think.)
Comment by Noam — July 28, 2009 @ 12:16 pm |
I like having a continuum between trivial and completely solved; it greatly increases the chance of an interesting partial result.
Presumably one can get O(n) simply by choosing one random n-bit number and then incrementing it until one finds a prime? The first moment method tells us that this works in polynomial time with high probability (and if one assumes some standard number theory conjectures, such as the k-tuples conjecture, one can make the success probability 1-o(1), see Emmanuel’s comment #6).
Comment by Terence Tao — July 28, 2009 @ 2:45 pm |
I don’t know whether there is a theorem/conjecture that Pr[there is a prime in the range [x, x+poly(n)]]>1/2 where x is chosen to be a random n bit integer (which is weaker than Cramer’s conjecture that states that the probability is 1).
The way to reduce the number of bits simply is to use what’s called “deterministic amplification”: There are ways to use O(n) random bits to create m=poly(n) random n-bit strings with the probability that one of them will hit any set of density 1/poly(n) (such as the primes) with very high probability.
The easiest way in this setting is to choose O(n) n-bit integers in a way that is pairwise independent — this requires only O(n) bits. An O(n)-step walk on a constant degree expander labeled with n-bit integers will also do the trick as shown in AKS.
Comment by Noam — July 28, 2009 @ 6:16 pm |
Thanks for the explanation! Regarding primes in short intervals, if we choose x to be a random n-bit integer and let X be the number of primes in [x, x+n], then the expectation of X is comparable to 1 (prime number theorem) and the second moment of X is O(1) (this can be seen from a bit of sieve theory, in fact all moments are bounded). This shows that X is positive with probability >> 1, which is enough for the naive algorithm I mentioned earlier to work.
Comment by Terence Tao — July 31, 2009 @ 5:21 am |
I may be completely off-base, but wouldn’t Ajtai-Komlos-Szemeredi help reducing the number of bits required? The idea is to lay out an (arbitrary) d-regular expander structure on the integers in the interval [n,n+m] and take a random walk on this graph. The probability of all steps of the walk avoiding the primes (a fairly large subset) should be very small.
Comment by Lior — July 28, 2009 @ 5:19 pm |
I don’t follow that suggestion. If you take a random walk until it mixes, then in particular you must be able to visit any vertex, so the walk must contain at least enough information to specify that vertex, which seems to suggest that the number of bits is at least log m. If the random walk doesn’t get to all vertices, then how do you know that the arbitary structure doesn’t happen to end just at composite numbers?
Comment by gowers — July 28, 2009 @ 5:35 pm |
If you are trying to hit a large set, you don’t need to wait for the walk to mix. The probability of all k steps of an expander walk avoiding a set of density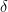 is bounded above by
is bounded above by 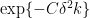 . For comparison, the probability of k uniformly chosen points avoiding the set is
. For comparison, the probability of k uniformly chosen points avoiding the set is 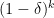 . In other words, if
. In other words, if 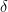 is fixed and generating a single uniform point costs
is fixed and generating a single uniform point costs  random bits then
random bits then  random bits give the same hitting probability as
random bits give the same hitting probability as 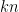 bits.
bits.
Now that I’m doing the calculation I can see that this bound by itself isn’t sufficient: in the interval [N,N+M] the density is of primes 1/log N, so we end up needing O(n^2) bits (n=log N) just for constant hitting probability. Noam’s comment (6:16) invokes more sophisticated technology I am not familiar with that can deal with sets of polylog density such as the primes.
Comment by Lior — July 28, 2009 @ 10:21 pm |
I still don’t quite follow. Let’s suppose you run the walk for a much smaller time k than it takes to mix. Then the proportion of vertices within k of your starting point will be small, and since the expander graph is arbitrary (your word) then there may simply be no primes within that radius. Or do you make the start point random? That might make things OK. (Or I could just be talking nonsense.)
Comment by gowers — July 28, 2009 @ 10:34 pm |
Sorry — yes, the starting point is chosen uniformly at random, and after that you walk on edges of the expander. Thus k steps cost you n+O(k) random bits — n for the initial point and O(1) for each further step.
Comment by Lior — July 28, 2009 @ 10:52 pm |
O(n) random bits actually suffices to obtain an almost uniform n-bit prime. This is a corollary of my unconditional pseudorandom generator with Nisan, because the algorithm to choose a random n-bit prime uses space O(n). Our PRG uses a random O(S) bit seed and outputs poly(S) bits which appear random to any space(S) machine (S>log n).
http://www.cs.utexas.edu/~diz/pubs/space.ps
Comment by David Zuckerman — July 29, 2009 @ 3:08 pm |
A similar idea that probably works in practice but is also hard to make deterministic is to take some integer n larger than 2, some set of generators of SL(n,Z), and do a random walk of length about k on SL(n,Z) with these generators, and then take the absolute value of the trace (or some other linear combination of coefficients) of the resulting matrix. One can expect this to be prime (and of size exponential in k) with probability about 1-1/k; using sieve, one can prove it to be “almost prime” (for certain sense of almost) with similar probability.
Comment by Emmanuel Kowalski — July 30, 2009 @ 3:20 pm |
Just a thought: If any primality test can be expressed as a constant-degree polynomial over a finite field from the digits of the number-under-test to {0,1}, then the known unconditional pseudorandom generators for polynomials can be used to derandomize finding primes the same way as under the full P=BPP derandomization assumption. So, instead of requiring a general PRG, the proposal is trying to put the primality test into a fully derandomizable subclass of P.
Comment by Martin Schwarz — August 2, 2009 @ 6:29 am |
Wow, it’s hard to resist the temptation to keep on thinking about this problem… fortunately (or not), I do have plenty of other things I need to do…
It occurs to me that if all large constructible numbers are smooth, then we may end up violating the ABC conjecture. Taking contrapositives, it is plausible (assuming factoring is easy) that if ABC is true, then we can find moderately large prime numbers in reasonable time (e.g. find primes of at least k digits in subexponential time, which as far as I know is still not known deterministically even on GRH).
Comment by Terence Tao — July 27, 2009 @ 8:46 pm |
This problem is sort of cute but it looks a better idea would be to discuss it first as “an open problem of the week” and get feedback from people in analytic number theory (and computational complexity if we allow some assumptions regarding derandomization.) Or discuss it privately with more experts in ANT/CC.
The advantage of this problem is that it is a sort of challenge to researcher in one area (analytic number theory) to respond to questions which naturally (well, sort of) arises in another area (you may claim that finding large primes was always on the table but this specific derandomization and computational complexity formulation wasn’t).
OK you can claim that if the challange to derandomize the primality algorithm was posed to number theorists early enough (say in 1940), this could have led to the results that the AKS primality testing was based on. But reversing the table seems like a long shot.
Comment by Gil Kalai — July 27, 2009 @ 9:47 pm |
That’s a good point. I’ll ask around.
It occurs to me that a problem which spans multiple fields may well be a perfect candidate for polymath; witness the confluence of ergodic theorists and combinatoralists for polymath1, for instance. Such projects are almost guaranteed to teach something, even if they don’t succeed in their ostensible goal.
Comment by Terence Tao — July 27, 2009 @ 10:00 pm |
Gil’s comment and this comment were very thought-provoking (to me).
Just to point what I think everyone knows instinctively, every polymath projects (that I have seen proposed) has an objective that is in complexity class NP.
This leads us to a mathematically natural question: what would a polymath-type project look like whose objective was in P? In other words, a project that was guaranteed to succeed … given commitment and competence on the part of the participants?
We can ask, does the class of P-Poly Projects have any interesting members?
My strong feeling is “yes” … in fact it seems plausible (to me) that P-Poly Projects are an exceptionally interesting and consequential subset of NP-Poly … but I wonder if anyone else is thinking along these lines?
Comment by John Sidles — July 28, 2009 @ 6:08 pm |
I never thought about this type of question(s) myself but I would think that the people in algorithmic/computational number theory (e.g., H. Cohen, K. Belabas, Lenstra, etc) would be the ones who have tried hardest to understand the problem — though presumably the standard software packages use fairly brute force techniques (that seems to be what Pari/GP does, with a “sieve” mod 210).
The question of what number theoretic conjecture are permitted makes the problem a bit fuzzy. For instance, how much of “primes in sequences” would be allowed? It’s known that, conditional on uniform versions of the k-tuple conjecture of Hardy-Littlewood, the number of primes between n and n+c(log n), where c is fixed, becomes asymptotically Poisson as n grows. This is independent of the Cramer model, and it is probably quite a solid conjecture. It doesn’t trivially solve the problem, as far as I can see, but it seems to be a strong tool to use.
Comment by Emmanuel Kowalski — July 27, 2009 @ 10:57 pm |
If we take c fixed and let n increase wouldn’t there be some point where the number of primes would be nonzero then we could just go through the interval n to n+c(logn) and test each one and that would take a polynomial amount of time in terms of the number of the digits which is roughly log n for the cases before the point we could just look at everything and add a large coefficient and the result is a polynomial algorithm.
Comment by Kristal Cantwell — July 31, 2009 @ 6:22 pm |
[…] Filed under: discussion, finding primes — Terence Tao @ 3:09 pm The proposal “deterministic way to find primes” is not officially a polymath yet, but is beginning to acquire the features of one, as we […]
Pingback by Deterministic way to find primes: discussion thread « The polymath blog — July 28, 2009 @ 3:09 pm |
Would P = BQP be a sufficient condition for an algorithm? Quantum computers don’t provide exponential speedup for search problems, but they have the advantage that factoring and discrete log are easy, and there is a polynomial-time speedup.
P = BQP is of course unlikely to hold in the “real world,” but it would imply lots of nice things: P = BPP, discrete log and factoring in P, without being as strong as P = NP or (I believe) P = promise-BPP. In addition, we can obtain some speedup on search problems and counting, although it’s only quadratic in general.
The other nice thing is that without assuming anything stronger, complexity-wise, than P = BQP, it seems impossible to abstract away the number-theoretic details. General search problems have a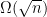 lower bound, as does approximate quantum counting — so in particular, the subinterval-density approach wouldn’t work without some number-theoretic trickery. This isn’t true for, e.g., P = NP, where general search problems are easy.
lower bound, as does approximate quantum counting — so in particular, the subinterval-density approach wouldn’t work without some number-theoretic trickery. This isn’t true for, e.g., P = NP, where general search problems are easy.
As much as I like complexity, it’s fiendishly hard (quantum doubly so), so take everything I just said with a grain of salt, and please correct me if I’m wrong.
Comment by Harrison — July 28, 2009 @ 6:17 pm |
R. C. Baker and G. Harman, “The difference between consecutive primes,” Proc. Lond. Math. Soc., series 3, 72 (1996) 261–280. MR 96k:11111
Abstract: The main result of the paper is that for all large x, the interval A=[x-x^0.535,x] contains prime numbers.
This is from the abstract at
http://primes.utm.edu/references/refs.cgi?long=BH96
and On the other hand, given any specific large number n, we can test it for primality in a deterministic manner in a time polynomial in the number of digits (by the AKS primality test).
It looks like this enough to get the desired result.
Comment by Kristal Cantwell — July 28, 2009 @ 6:45 pm |
This won’t work without more tricks because one would need to test exponentially many integers (with respect to the number of digits) before being sure to find a prime.
From the purely number-theoretic point of view, the question seems to be roughly as follows: can one describe (deterministically), for all large X, a set of integers of size polynomial in log(X), each of them roughly of size X, such that this set is sure to contain a prime?
I think the best (number-theoretic, i.e., not Cramer-model based or similar) known results about this are in the paper “Primes in short intervals” of H. Montgomery and K. Soundararajan (Communications in Math. Phys. 252, 589–617, 2004). They give strong evidence for what the number of primes between X and X+H should look like when H is a function of X of various type, and X grows. Again, the results are convincing conjectures, but the number-theoretic assumptions are very strong.
Comment by Emmanuel Kowalski — July 28, 2009 @ 8:53 pm |
In a paper of Impagliazzo,
http://www.cs.ucsd.edu/users/russell/average.ps
five worlds (Algorithmica, Heuristica, Pessiland, Minicrypt, Cryptomania) were identified in complexity theory… perhaps we can determine now whether deterministic primality finding is easy in some of these worlds?
Comment by Terence Tao — July 28, 2009 @ 7:33 pm |
(Here is a post reviewing these five worlds . )
Comment by Gil Kalai — July 28, 2009 @ 8:22 pm |
If P = NP, we’re done. (If we’re assuming P = BPP, this covers most if not all of Algorithmica; the situation where P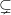 NP
NP 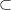 BPP is sad and confusing.)
BPP is sad and confusing.)
Is the Hastad-Impagliazzo-Levin-Luby PRNG strong enough to derandomize checking primes for us? I think it is, but I can’t seem to find the paper. If so, Minicrypt and Cryptomania have unconditional deterministic primality finding.
Heuristica seems approachable: Since factoring is “almost always easy,” and sufficiently large numbers will almost always have some large enough prime factor, a good strategy might be to pick a very large number and factor it. Of course, this is neither deterministic nor guaranteed to be in polynomial time. Can this be made rigorous, say under the assumption that P = BPP?
Pessiland looks like the hardest world; I’m not even sure I could start on a list of conditions under which we might have efficient primality finding.
Comment by Harrison — July 28, 2009 @ 9:01 pm |
Here’s a thesis in French by Pierre Dusart that is worth a nod in the bibliography:
Autour de la fonction qui compte le nombre de nombres premiers
It explicates previous results and includes a proof that for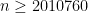 there is always a prime between
there is always a prime between  and
and 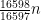 .
.
Comment by Jason Dyer — July 28, 2009 @ 7:52 pm |
My ICM paper has several pointers to the literature on pseudorandomness and derandomization:
http://arxiv.org/abs/cs.CC/0601100
The question of deterministically finding large primes is mentioned on page 4. (I didn’t come up with it, I heard it from either Avi Wigderson or Oded Goldreich.)
One remark is that this problem (like many “explicit construction” problems) is a special type of derandomization problem. If you think of it as the problem “given n, output an n-bit prime,” then this is a problem that can be solved, with high probability, in randomized exponential time (exponential because the input n has a log n bit representation, while the running time of the algorithm is polynomial in n), and we would like to solve it in deterministic exponential time.
“Derandomizing” exponential time randomized algorithms is an “easier” task than derandomizing polynomial time ones, in the sense that a universal method to derandomize polynomial time algorithms also implies a universal method to derandomize exponential time algorithms, but the reverse is not clear.
Comment by luca — July 28, 2009 @ 10:05 pm |
two quick thoughts,
1) Robin Pemantle and some other have a paper that touches on a related problem I think : http://www.math.upenn.edu/~pemantle/papers/Preprints/squares080204.pdf
2) On thing to help guide what is a realistic statement to prove re construct a k-bit prime in time poly(k) might be to look at how that procedure could then be used to factor n>k bit numbers via enumerating primes with <n bits. Or at the very least, it might help rule out statements that are potentially too strong.
Comment by cartazio — July 29, 2009 @ 1:44 am |
Before this project is fully launched, I think it would be good to get some idea of what people think they might be able to contribute to it, so we can see whether there would be a core of people, as there was for DHJ, who were ready to follow it closely and attempt seriously to push the discussion towards a solution of the problem.
My own personal feelings about this particular problem are that I find it quite easy to imagine making preliminary remarks of the kind that have already been made, but quite difficult to imagine getting my teeth into an approach that feels as though it could lead to a solution. (This is in contrast with DHJ, where there seemed to be a lot of avenues to explore right from the beginning, so we didn’t have to wait for someone to have an unexpected idea to get things going properly.) But this feeling could change very rapidly if, as seems quite possible, people started coming up with relevant questions that didn’t seem impossible to answer. For example, as Emmanuel mentioned above, one way of thinking of the problem is as a search for a set of at most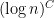 numbers near
numbers near  , at least one of which has to be prime. The most obvious thought is to take a sufficiently long interval, but we don’t know how to prove that it contains a prime, even with the help of GRH. Are there any other proposals? All I can think of is conjectures that seem impossible to prove (such as that if you find a suitably rich supply of very smooth numbers and add 1 to them, then at least one of the resulting numbers is prime) or not strong enough (such as that if you apply the “W-trick” and pass to an arithmetic progression with common difference the product of the first few primes, you’ll get a higher density of primes inside it). But if somebody came up with an idea, or better still, a class of ideas, for constructing such a set, then there would be a more specific and possibly easier problem to think about. Somehow, it doesn’t feel to me as though I’m going to be the one who has the clever idea that really gets things started, so after the initial activity I think I’d find myself waiting for somebody else to have it. So I think I’d be an occasional participator, unless something happened that turned the problem into one that I felt I had lots of ways to attack.
, at least one of which has to be prime. The most obvious thought is to take a sufficiently long interval, but we don’t know how to prove that it contains a prime, even with the help of GRH. Are there any other proposals? All I can think of is conjectures that seem impossible to prove (such as that if you find a suitably rich supply of very smooth numbers and add 1 to them, then at least one of the resulting numbers is prime) or not strong enough (such as that if you apply the “W-trick” and pass to an arithmetic progression with common difference the product of the first few primes, you’ll get a higher density of primes inside it). But if somebody came up with an idea, or better still, a class of ideas, for constructing such a set, then there would be a more specific and possibly easier problem to think about. Somehow, it doesn’t feel to me as though I’m going to be the one who has the clever idea that really gets things started, so after the initial activity I think I’d find myself waiting for somebody else to have it. So I think I’d be an occasional participator, unless something happened that turned the problem into one that I felt I had lots of ways to attack.
There’s also the possibility that it would go off in a direction that would require a better knowledge of analytic number theory than I have. In that case, I would become a passive (but interested) observer.
Comment by gowers — July 29, 2009 @ 10:22 pm |
On the analytic number theory side I’d be ready to participate as much as I can. I have no competence in complexity theory, although I will try to at least learn the terminology…
Comment by Emmanuel Kowalski — July 30, 2009 @ 12:51 am |
I agree with Tim, it seems all the approaches boil down to the same thing: find a sufficiently large interval (but not too large) and then prove that this interval contains a prime.
Unfortunately there do not as of yet seem to be any really promising new ideas on how exactly to do this (other than solving some long standing open conjectures).
I would love to be wrong of course and hope the experts can see some serious “cracks” that would allow progress to be made.
Otherwise I see people discussing it for 2-3 weeks and then putting it back on the shelf.
Comment by rweba — July 30, 2009 @ 1:44 am |
It occurred to me to wonder if the existence of an efficient algorithm to generate primes might imply (and thus be equivalent to) the existence of a pseudorandom generator? The intuition is simply that under sufficiently strong assumptions about the presumed randomness of the primes, it seems like a prime-generating algorithm might be useful as a source of randomness.
If this line of thought can be made to work, one might hope to prove that under some conjecture that implies randomness in the primes, the existence of pseudorandom generators is equivalent to being able to find primes deterministically.
Comment by Michael Nielsen — July 30, 2009 @ 12:03 pm |
This will imply that Cramer conjecture on the distributions of primes implies the existence of pseudorandom generator; Is it reasonable?
Comment by Gil Kalai — July 30, 2009 @ 12:38 pm |
The deterministically found primes might have special regularity properties (e.g., they might be congruent to 1 modulo a largish deterministically determined number, or satisfy more complicated algebraic conditions) that make them less random than the general primes. In fact, one may suspect that an algorithm to construct primes is likely to extract those with a particular property.
Comment by Emmanuel Kowalski — July 30, 2009 @ 3:16 pm |
Yes, I would think think this is asking rather too much…
Comment by Ryan O'Donnell — July 31, 2009 @ 7:20 am |
I wonder about the intuition itself here, and not just whether it can be converted into a solid argument. Suppose the primes are in some sense very random, and we have an algorithm that gives us a prime in![[n,n+m]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2Bm%5D&bg=ffffff&fg=000000&s=0&c=20201002) whenever
whenever  isn’t too small. The randomness of the primes alone will not make this a pseudorandom generator, because there is a polynomial-time algorithm for recognising primality. So whatever it is that makes it a pseudorandom generator needs to be some additional ingredient. (Of course, one could try to transform the output somehow, but then it seems that what would make it a PRG would come from the transformation.)
isn’t too small. The randomness of the primes alone will not make this a pseudorandom generator, because there is a polynomial-time algorithm for recognising primality. So whatever it is that makes it a pseudorandom generator needs to be some additional ingredient. (Of course, one could try to transform the output somehow, but then it seems that what would make it a PRG would come from the transformation.)
Comment by gowers — July 31, 2009 @ 8:33 am |
Is there any sequence which we can describe by a formula or a simple algorithm on which we can expect that the primes will behave “nicer” (larger density, smaller gaps etc.) than on the sequence of all integers? E.g. sequences like 2^n-1, n!+1
It would be nice if some sort of negative results hold (which would be a Direchlet type result); that any bounded-complexity attempt to produce a sequence of integers must yield a sequence with density of primes, gaps between primes, etc. upper bounded by the behavior on all the integers.
Comment by Gil Kalai — July 30, 2009 @ 3:53 pm |
It looks that I do not know how to phrase this question formally. I would like to distinguish complexity theoretically between a sequence of the form a(n)=3n+4 or a(n)=n^2+1 or a(n)=2^n+1 or a(n)=n!+1 or perhaps even a(n) = p_1 p_2…p_n +1 or perhaps even “we choose every integer with probability 1/2 and a(n) is the nth integer”
FROM
a(n) is described by running primality algorithm on the integers one by one and taking the nth prime.
Comment by Gil Kalai — July 30, 2009 @ 6:17 pm |
What about arithmetic progressions?
So this could be something like “Between p and 2p we can explicitly identify an arithmetic progression which is guaranteed to contain at least one prime within the first log(p) terms.”
This appears very unlikely (I didn’t find any results of that type in a quick search) but perhaps some other clever sequence can be found.
Comment by rweba — July 31, 2009 @ 1:18 am |
In fact, typically if a sequence is chosen so that it satisfies the “obvious” congruence restrictions to contain infinitely many primes, it is expected to contain more than what might be thought. E.g. for arithmetic progressions modulo q, the density of primes is 1/phi(q) (for permitted classes) against 1/q for integers themselves in the same class.
Comment by Emmanuel Kowalski — July 31, 2009 @ 2:03 am |
One possible conjecture would be that if a sequence a(n) is described by a bounded depth polynimial size (in log n) arithmetic circuit (even allowing randomization)then the density of primes in the sequence goes to zero.
Comment by Gil Kalai — July 31, 2009 @ 7:07 am |
Perhaps a finite field version would be easier? e.g., given a fixed finite field F, to deterministically find an irreducible polynomial P(t) of degree k (or more) in F[t]? Perhaps this is trivial though (are there explicit formulae to generate irreducible polynomials over finite fields?)
Comment by Terence Tao — July 31, 2009 @ 6:04 am |
…and what about polynomial with rational coefficients? in this case factoting is polynomial by a theorem of Lenstra, Lenstra and Lovasz. http://www.math.leidenuniv.nl/~hwl/PUBLICATIONS/1982f/art.pdf
Comment by Gil Kalai — July 31, 2009 @ 7:00 am |
Well, there is a paper by Adelman and Lenstra titled “Finding irreducible polynomials over finite fields” that does this. And there is a paper by Lenstra and Pomerance titled “Primality testing with Gaussian periods” that references it and is worth looking at (in fact, this paper is where I first learned of the Adelman-Lenstra result, as I heard Carl speak on it at a conference). Of course if you could find a irreducible polys of degree exactly k, then you could deterministically produce quadratic non-residues modulo primes, an open problem, using traces.
Comment by Ernie Croot — July 31, 2009 @ 3:13 pm |
This is in regard to the problem of finding irreducible polynomials. The best known deterministic algorithm for finding an irreducible polynomial of degree d over a given finite field of size p^r has running time poly(dpr). In particular, if the characteristic p is itself a part of the input then no deterministic polynomial-time algorithm is known. On the other hand, when the characteristic is fixed then the algorithm is efficient in the sense that it has running time poly(size of input + size of output). Over the rational numbers we have very explcit irreducible polynomials: x^m – 2 is irreducible for all m >= 1 (Eisentein’s irreducibilty criterion, http://en.wikipedia.org/wiki/Eisenstein's_criterion).
Comment by Neeraj Kayal — August 1, 2009 @ 4:26 pm |
There’s also a paper of Victor Shoup (“New algorithms for finding irreducible polynomials in finite fields”) which takes only (power of log p)*(power of n) to deterministically find an irreducible polynomial of degree n in F_p[t], GIVEN an oracle that supplies certain non-residues in certain extensions of F_p. I haven’t looked at this in any detail so don’t know whether the ideas are of any use for the present problem.
Comment by JSE — August 6, 2009 @ 4:10 am |
This is continuing a line of thought initiated by Gil, which I can no longer find (does that say something about me or about the organization of the comments?). The idea was to assume that we have an oracle that will factorize numbers instantly and to use that to find a polynomial-time algorithm for producing primes. (Ah, found it now. I suddenly had the idea of searching for “pigs”, which led me back to Gil’s comment 3 and one of his further comments in the replies to 3.)
The idea is that all we now have to do is find a small set that is guaranteed to have a number with a prime factor of k digits. We know that a “typical” number n has about prime factors, so it can reasonably be expected to have prime factors of size about
prime factors, so it can reasonably be expected to have prime factors of size about  . So to find a prime near
. So to find a prime near  it makes sense to factorize numbers of size about
it makes sense to factorize numbers of size about 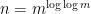 (this function approximately inverts the function
(this function approximately inverts the function  ). Note that if
). Note that if 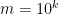 then
then  is about
is about 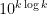 , so the number of digits has not gone up by much, which is good if we are looking for a polynomial-time algorithm.
, so the number of digits has not gone up by much, which is good if we are looking for a polynomial-time algorithm.
How might one go about proving that there are very small intervals of numbers that are guaranteed to contain numbers with prime factors of size about ? Here is a rough approach. Start with some interval
? Here is a rough approach. Start with some interval 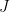 of numbers near
of numbers near  that’s guaranteed to contain plenty of primes, using the prime number theorem, say. We now want to prove that the iterated product set
that’s guaranteed to contain plenty of primes, using the prime number theorem, say. We now want to prove that the iterated product set  is very dense — so much so that it has to intersect every interval of width at least
is very dense — so much so that it has to intersect every interval of width at least 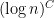 .
.
This is a problem with an additive-combinatorial flavour. We can make it even more so by taking logs. So now we have a set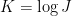 (by which I mean
(by which I mean 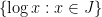 ) and we would like to prove that the iterated sumset
) and we would like to prove that the iterated sumset 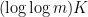 , or more accurately
, or more accurately 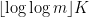 , is very dense. The sort of density we would like is such that it will definitely contain at least one element in the interval
, is very dense. The sort of density we would like is such that it will definitely contain at least one element in the interval ![[\log n,\log(n+(\log n)^C)]](https://s0.wp.com/latex.php?latex=%5B%5Clog+n%2C%5Clog%28n%2B%28%5Clog+n%29%5EC%29%5D&bg=ffffff&fg=000000&s=0&c=20201002) , which is roughly
, which is roughly ![[\log n,\log n+n^{-1}(\log n)^C]](https://s0.wp.com/latex.php?latex=%5B%5Clog+n%2C%5Clog+n%2Bn%5E%7B-1%7D%28%5Clog+n%29%5EC%5D&bg=ffffff&fg=000000&s=0&c=20201002) . This may look an alarmingly high density, but in
. This may look an alarmingly high density, but in  itself we have lots of pairs of elements that differ by at most
itself we have lots of pairs of elements that differ by at most  , so it doesn’t seem an unreasonable hope.
, so it doesn’t seem an unreasonable hope.
The kind of thing that could go wrong is that every prime near turns out to lie in some non-trivial multidimensional geometric progression, which then stops the iterated sumset spreading out in the expected way. But that seems so incredibly unlikely that there might be some hope of proving that it cannot happen, especially if one is allowed to use plausible conjectures. I’m reminded of results by Szeméredi and Vu connected with conjectures of Erdos about iterating sumsets of integers on the assumption that they don’t all lie in a non-trivial arithmetic progression. I can’t remember offhand what the exact statements are, but they seem to be in similar territory.
turns out to lie in some non-trivial multidimensional geometric progression, which then stops the iterated sumset spreading out in the expected way. But that seems so incredibly unlikely that there might be some hope of proving that it cannot happen, especially if one is allowed to use plausible conjectures. I’m reminded of results by Szeméredi and Vu connected with conjectures of Erdos about iterating sumsets of integers on the assumption that they don’t all lie in a non-trivial arithmetic progression. I can’t remember offhand what the exact statements are, but they seem to be in similar territory.
I realize that I am slightly jumping the gun by posting a comment like this. My defence is twofold. First, I will be in an almost entirely internet-free zone from tomorrow for a week. Secondly, this comment is indirectly a comment about the suitability of this problem to be a Polymath project, since it shows that there are subproblems that one can potentially get one’s teeth into (though it may be that someone can quickly see why this particular angle is not a fruitful one).
Comment by gowers — July 31, 2009 @ 9:02 am |
In connection with the above, does anyone know the work of Goldston, Pintz and Yildirim (without the dots on the i’s) well enough to know whether it says more than just that the difference between successive primes is often small? For example, must the difference often be very close to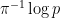 ? This would have some relevance to the additive-combinatorial structure of the set
? This would have some relevance to the additive-combinatorial structure of the set  above.
above.
Comment by gowers — July 31, 2009 @ 9:18 am |
I would have to check the precise details, but from my memory, the Goldston-Pintz-Yildirim results do not give any particular information on the location of the primes, except for giving intervals in which one is guaranteed to find two of them.
Comment by Emmanuel Kowalski — July 31, 2009 @ 3:32 pm |
This sounds like smooth numbers in short intervals, assuming I haven’t missed the precise dependence of parameters. There is an old result of Balog which says that intervals [x,x+x^(1/2 + epsilon)] contain numbers that are x^(epsilon)-smooth (i.e. all prime factors smaller than about x^epsilon), or thereabouts (so the interval width is quite large — of size x^(1/2)). There are refinements due to Granville, Friedlander, Pomerance, Lagarias, and many others (including myself). It’s a very hard problem. You might check out Andrew Granville’s webpage, as he has a few survey articles on smooth numbers (at least two that I know of).
Comment by Ernie Croot — July 31, 2009 @ 2:04 pm |
Presumably there are results of the type “for almost all x, the interval [x,x+h(x)[” contains
some type of smooth/friable number (the smoothness/friability depending on h(x)), with functions h(x) much smaller than x^{1/2}? (I don’t know a reference myself, but this type of variant of gaps of various types is quite standard).
Comment by Emmanuel Kowalski — July 31, 2009 @ 3:30 pm |
Yes, I think Friedlander has some results along those lines.
Comment by Ernie Croot — July 31, 2009 @ 3:35 pm |
In fact, there are two papers that are relevant: Friedlander and Lagarias “On the distribution in short intervals having no large prime factors”, and Hildebrand and Tenenbaum’s paper “Integers without large prime factors”. The intervals widths are still much larger than a power of log x, though.
Comment by Ernie Croot — July 31, 2009 @ 3:44 pm |
You may well be right that it’s a very hard problem, but if one weakened the aim to finding a prime with at least k digits (rather than exactly) then one wouldn’t care about large prime factors. Indeed, the aim would be more like to find a number that isn’t smooth. But also, we are looking for normal behaviour rather than atypical behaviour: the aim would be to show that in every short interval there is a number that has a prime factor of about the expected size, and for the weaker problem it would be enough to show that there is a number that has not too many prime factors. This is asking for something a lot weaker than smoothness.
smoothness.
Comment by gowers — July 31, 2009 @ 4:44 pm |
That sounds a lot more hopeful than the smooth numbers in short intervals approach. Though, since you still need to work with quite short intervals, of width (log x)^c, probably the usual “Dirichlet polynomial” methods of Balog and others won’t work.
However, some of the constructions of Lagarias and Friendlander might work, but I doubt it.
I would probably try to find primes with at least k digits by another method.
Comment by Ernie Croot — July 31, 2009 @ 6:07 pm |
Regarding Tim’s nice idea here, at first I had the following thought: Assuming factoring is in P is a very strong assumption (especially considering that the assumption’s negation is the basis of a lot of modern cryptography). Still, we actually *have* factoring algorithms that work on n-digit numbers in time 2^{n^{1/3}} or so. And finding n-digit primes deterministically in time 2^{n^{1/3}} would be pretty great (far better than the 2^{n/2} one gets out of ERH).
But then I realized that the fastish factoring algorithms are almost surely randomized :( And indeed, it seems from a 1-minute literature search that the fastest known *deterministic* factoring algorithms take time like 2^{cn} for some fraction c, even heuristically.
Comment by Ryan O'Donnell — July 31, 2009 @ 5:57 pm |
As far as I can see, the Quadratic Sieve isn’t randomized. Heuristics predict that it runs in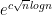 steps (where
steps (where  is the number of digits.)
is the number of digits.)
However, it is true that those heuristics are probably more difficult to make rigorous than the ones concerning primes in short intervals.
Comment by David Speyer — August 1, 2009 @ 1:54 pm |
Maybe, for start, we can ask to find (in a polynomial time deterministic algorithm) a prome number with at least k digits. Now coninuing Tim’s line of thought (based on taking factoring for free) maybe it is true (provable??) that among any 10 consecutive integers with k^3 digits (say) there is always one with a prime factor having at least k digits?
Comment by Gil Kalai — July 31, 2009 @ 7:14 pm |
From probabilistic reasoning alone that should probably be false, but if you replace 10 with, say, k^c, then probably what you say is true. My reasoning as to why what you say is false goes as follows: let x = 10^(k^3). We want to show that there is an integer of size about x such that x,x+1,…,x+9 are all (10^k)-smooth. The probably that a random n < x is (10^k)-smooth is something like (10^{-k^2}); so, we would certainly expect there to be 10 in a row that are (10^k)-smooth.
Of course you mean to allow 10 to be a power of k.
Comment by Ernie Croot — July 31, 2009 @ 7:26 pm |
Dear Ernie, I see (except that the probability you mention becomes smaller when k is larger so probably you meant something else). I suppose we go back to the question of showing that among polylog(k) consecutive integers with k^10 digits there is one which is not 10^k smooth. This looks like a Cramer’s type conjecture but as Tim said maybe it is easier.
Although it is getting further away from the original problem I am curious what could be a true statement of the form among T consecutive integers larger than U one must be B-smooth; and how far such a statement from the boundary of what can be proved.
Comment by Gil — July 31, 2009 @ 7:58 pm |
Dear Gil, first regarding your parenthetical comment, I was trying to work out in my head exactly what it is in terms of k. Let’s see if I got it right… the theorem I was thinking of says that the number of n < x that are exp( c (log x loglog x)^(1/2))-smooth is about x exp( -(1/2c) (log x loglog x)^(1/2)), and this holds, I believe, even when c is allowed to depend (weakly) on x. So, if you take c to be something like (log x)^(-1/6) times some loglog's, then you are looking at exp( (log x)^(1/3})-smooth numbers — in other words, the smoothness bound has the 1/3-root as many digits as x. And, the number of these exp((log x)^(1/3}) up to x should be something like x exp( -(1/2 (log x)^(-1/6)) (log x loglog x)^(1/2}), which is something like x exp(-(log x)^(2/3)). So, the probability of picking one of these smooths is something like exp(-(log x)^{2/3}). Now, if x = 10^(k^3), then this probability is something like 10^(-k^2), with some log k factors thrown into the exponent. So, it seems what I wrote is correct, modulo some lower order terms.
I think that Tim's question is a lot, lot easier than Cramer's conjecture, but both of them seem quite difficult.
As to your last question, probably it is true that if B is a power of log(U), then T is bounded. This is because, the number of (log x)^c -smooths up to x grows like a power of x; for example, the # of (log x)^(1/2) -smooths up to x is something like x^(1/2), so you wouldn't expect there to be more than 3 of them in a row up to x. Proving such a result is probably quite hard, though, again, nowhere *near* as hard as Cramer.
Comment by Ernie Croot — July 31, 2009 @ 8:15 pm |
Well, we can be less ambitious than getting a -digit prime in polynomial time, and be happy with getting a
-digit prime in polynomial time, and be happy with getting a 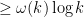 -digit prime in polynomial time, where
-digit prime in polynomial time, where  as
as 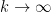 ; this is equivalent to finding a
; this is equivalent to finding a  -digit prime in subexponential time
-digit prime in subexponential time  . Note that brute force search (as in Klas’s comment below) gives all primes of
. Note that brute force search (as in Klas’s comment below) gives all primes of 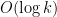 digits in size, so we only have to beat this by a little bit.
digits in size, so we only have to beat this by a little bit.
The task is now to exclude the scenario in which every integer in the interval![[10^k, 10^k + k]](https://s0.wp.com/latex.php?latex=%5B10%5Ek%2C+10%5Ek+%2B+k%5D&bg=ffffff&fg=000000&s=0&c=20201002) (say) is
(say) is 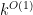 -smooth. It sounds like a sieve would be a promising strategy here.
-smooth. It sounds like a sieve would be a promising strategy here.
One can use the “W-trick” to give a small boost here, actually (again related to Klas’s comment). Let W be the product of all the primes less than , then W has size about
, then W has size about 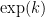 . Instead of working with an interval, we can work with the arithmetic progression
. Instead of working with an interval, we can work with the arithmetic progression 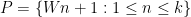 . The point is that these numbers are already coprime to all primes less than
. The point is that these numbers are already coprime to all primes less than  .
.
So the question is now: can one rule out the scenario in which all elements of P are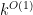 -smooth?
-smooth?
Comment by Terence Tao — August 1, 2009 @ 2:23 am |
This also seems like an immensely hard problem for sieves. One reason is that sieves are typically
insensitive to the starting point of the sieve interval, and in this case we know that [1,k] certainly
consists only of y := k^{O(1)}-smooth numbers.
Furthermore, it is hard to imagine such techniques as linear forms in logarithms working, as
here one has too many logs: if n, n+1, …, n+k are all y-smooth, then taking logs one has relations
like
log(n+1) – log(n) = O(1/n),
and then expressing log(n+1) and log(n) in terms of logs of their respective small prime factors, one gets
a linear form. In fact, one gets a system of linear forms (because there are k+1 smooth numbers), but
unfortunately the linear forms inequalities are too weak to tell you much, as you use ~ y/log(y) logs.
Still, there may be some way to amplify what the usual LLL inequalities give, because you have so many
different forms to work with.
There may be a way to use polynomials somehow. For example, if n is y-smooth, and is of size about 10^k,
then you can treat n as a special value of a smooth polynomial: for example, say
n = p_1 … p_t, p_i T – O(sqrt(T)) or so
in the case where the |a_i| <= T.
An F_p analogue of Mason's theorem might also be helpful here, since if we mod these polynomials out
by a small prime they typically are no longer square-free — they will be divisible by lots of linear
polynomials to large powers.
Even if we can't get sufficient control on the size of the coefficients, one might be able to use the
special form of these polynomials to conclude that there aren't too many integers n < 10^k where
n,n+1,…,n+k are all y-smooth; and furthermore, it might be possible to say just enough about the
structure of there exceptional n's to know how to avoid them (i.e. pick an n such that
n (n+1)…(n+k) is not y-smooth).
Also, we don't need to restrict ourselves to polynomials of just one variable x. Often one gets must better results
when one works with many variables, as in the proof of the Roth's theorem on diophantine approximation.
Comment by Anonymous — August 3, 2009 @ 4:31 pm |
Assuming that factoring is free here is another possibility which seems, some old computational work, to produce large primes.
1 Find the first k primes p_1….p_k. This can easliy be done by using a sieve.
2. Let a_k = 1+p_1p_2…p_k . The product can be computed is cheaply using Fourier transform. This is the “product plus one” from Euclid’s proof of the infinitude of primes, which is usually not a prime.
3. Find the largest prime factor of a_k. This number oscillates with k but on the average seems to have a number of bits which is, at least, linear in k.
I don’t know if one can prove that this actually produces a sequence of large primes, but trivially it does produce a sequence of numbers a_k which are not smooth.
Comment by Klas — July 31, 2009 @ 9:32 pm |
Dear Terry,
I have been working on this problem for sometime now. I found that there is an association between Mersenne numbers and prime numbers. That is each Mersenne is link to a particular prime/s. In such a way that for any given Mersenne the associated prime/s can be determined. The cramer’s conjecture of N and 2N as maximum distance between two adjacent primes reflects the relationship between two consecutive Mersennes which is M and 2M + 1. That is, in one instance two consecutive Mersennes primes has the cramer’s rule condition of distance of 2m + 1(this is fact may turn out to be the only condition).
I am currently working on the algorithm using combinatorial binary model.
Comment by jaime montuerto — July 31, 2009 @ 4:34 pm |
More on Mersenne connection, given a range x how many primes are there in that region? According to Gauss it would be about log2 x. If we rephrase the question to how many mersennes are there in that region? It would be really about log2 x. Unfortunately the primes that associated with those mersennes are not in that region but far below the region of x unless it’s a mersenne primes. But if we get all the primes associated with all the mersennes below x, we can use that to sieve out all the multiples in region x, for each mersennes primes cycles according to its mersenne.
So all the primes in the region their mersennes associates are far up the scale except the mersenne primes in the region. Although the ration of primes to its Mersennes behave randomly it averages out evenly and that reflects the distribution of log2 x and reflects the number of primes is the number of mersennes. It’s more tempting to say that the distribution of primes is the distribution of mersennes.
The subtle connection of randomness is not much the binary width of the prime numbers in relation to its mersenne and not the number of bits in prime but the subtle distribution of bits within the prime number itself. A number that has bits highly equidistant say like palindromic or cyclotomic in bits distribution is likely to be a composite while the more random or more unique distances to each other the more likely it would be prime numbers. My investigation is on this area of grammar like property.
On prime between mersennes is akin to conjecture that a prime exists between N and 2N.
Comment by jaime montuerto — July 31, 2009 @ 9:02 pm |
Not a reply to any specific comment, but another in the rapidly developing tradition of chasing round strange implications amongst all these conjectures. I’m not quite sure of my facts here, so this is an advance warning of possible stupid assertions to follow.
The idea is this. If factorizing is hard, then discrete log is hard. If discrete log is hard, then there is a PRG. If there’s a PRG, then we can use a pseudorandom search for primes with digits instead of a genuinely random search, and it is guaranteed to work. But this means that there is some set of size about
digits instead of a genuinely random search, and it is guaranteed to work. But this means that there is some set of size about  of numbers with
of numbers with  digits each, at least one of which is guaranteed to be prime. But if one thinks what the output of a PRG constructed using the hardness of discrete log is actually like, it is quite concrete (I think). So we have found a very small set of integers, at least one of which is guaranteed to be prime.
digits each, at least one of which is guaranteed to be prime. But if one thinks what the output of a PRG constructed using the hardness of discrete log is actually like, it is quite concrete (I think). So we have found a very small set of integers, at least one of which is guaranteed to be prime.
As Terry pointed out earlier, there are problems in using the hardness of discrete log because first you need some large primes. Otherwise one might have a programme for finding an indirect proof of existence of a deterministic algorithm: either factorizing is hard, in which case build a PRG, or it is easy, in which case try to find a non-smooth number somewhat bigger than and factorize it.
and factorize it.
Comment by gowers — July 31, 2009 @ 8:42 pm |
I believe the PRG you get from the hardness of discrete log (or RSA for that matter) does not have the right properties for this to work. Namely, if you only use a logarithmic length seed (in k) you only appear random to polylogarithmic (in k) time algorithms. In particular, using this generator to make k bit integers might always give you composites. I do not think there is any easy way around this difficulty, as people have grappled with it before when trying to derandomize BPP.
You could get a PRG with the same properties directly by using multiplication as a one way function, if factoring is actually hard on average, without having to deal with generating primes. I don’t have a reference for this, but I’m sure you could find one in the cryptography literature. As I said, I don’t think this will get you to logarithmically many random bits, but it may be able to get you to o(n) random bits.
Comment by Paul Christiano — August 1, 2009 @ 12:16 am |
Ah. Well in that case I have to make the rather less interesting observation that proving the existence of any PRG has startling number-theoretic consequences (in the form of very small sets that are guaranteed to contain primes). But (i) there are good Razborov-Rudichy reasons for thinking that proving the existence of a PRG is very hard, and (ii) if we’re afraid of those number-theoretic consequences then we should be afraid of this whole project …
Comment by gowers — August 1, 2009 @ 7:30 am |
A less ambitious goal might be to show an analog of Cramer’s conjecture for square-free numbers: say that there is always a squarefree number in the interval [n, n+log^2(n)].
This is less ambitious because the squarefree numbers have a constant density in the integers (as opposed to the primes whose density is inverse logarithmic). Is anything along these lines known? Also the analogous problem for finite fields – finding squarefree polynomials – is easy.
Comment by Neeraj Kayal — August 1, 2009 @ 4:46 pm |
There is a result due to Michael Filaseta and Ognion Trifinov, but the interval width is only a power of n, not a power of log n.
Comment by Ernie Croot — August 1, 2009 @ 6:19 pm |
And here also, in for almost all intervals, one can get a better result; in fact Bellman and Shapiro (“The distribution of squarefree integers in small intervals”, Duke Math. J. 21, (1954). 629–637) show — quite easily: no L-functions or real sieve is involved — that for any fixed function phi(n) which grows to infinity, it is true that for almost all n, the interval [n,n+phi(n)] contains a squarefree number.
I would say that there might be some chance indeed of finding an algorithm to construct squarefree numbers of arbitrary size in polynomial time, even if primes are not accessible.
Comment by Emmanuel Kowalski — August 2, 2009 @ 12:14 am |
Let me just point out that it is easy to construct square-free numbers of arbitrary size, as you just need to product together lots of very small primes.
Comment by Ernie Croot — August 2, 2009 @ 12:49 am |
Of course…
Comment by Emmanuel Kowalski — August 2, 2009 @ 1:57 am |
A pure probabilistic approach to identifying a prime number is tuned to using particular tools to show that success is likely after not-too-much time. However, testing one number after another chosen at random does throw away information – it will only be useful information if it can be used to make the next choice better-than-average: could this be possible?
Or alternatively, is there a slightly more expensive algorithm for checking primality which yIelds such useful information if a number is found to be composite?
Comment by Mark Bennet — August 1, 2009 @ 9:15 pm |
But wouldn’t such an approach apply to most other situations as well? In particular, how would such an approach get the result we want without proving P = RP?
Comment by Jacob Steinhardt — August 2, 2009 @ 4:59 am |
Well, of course, if there were an effective way of using “information” otherwise discarded, it might prove something – that was the point of my post. However, it may be that any gains would be so marginal as to make no difference to the complexity class, or indeed that there is no real information to be extracted.
The various algorithms and proofs have been optimised for other problems – in various places (smooth v non-smooth, for example) it seems clear that the current formulation is asking a different kind of question from that which has previously been addressed. I just wanted to point out that here, and perhaps in other places, there is a potential leakage of information – and where this is the case, there may be opportunities for optimisation or improvement of strategies to deal with slightly different problems.
It may come to nothing, but there are some points to be explored. And there may be some useful progress or insight, even if there is no full proof.
Comment by Mark Bennet — August 2, 2009 @ 9:16 pm |
I was thinking about the question of whether the finding primes problem can be solved purely by “soft” (or more precisely, relativisable) complexity theory techniques, using no number-theoretic information about the primes, other than that they are dense and lie in P (i.e. testing primality can be done in polynomial time). I think I almost have an argument that this is not possible (at least without additional complexity hypotheses), i.e. given the right oracle, there exist a set of “pseudoprimes” which are dense and in P (and thus can be easily located by probabilistic algorithms), but for which one cannot write down a deterministic algorithm that locates large pseudoprimes in polynomial time. But it needs a slight fix to work properly; perhaps some computational complexity expert will see how to fix it?
Here’s how it (almost) works. Let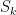 be the set of k-digit integers which have a Kolmogorov complexity of at least
be the set of k-digit integers which have a Kolmogorov complexity of at least 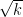 , i.e. they require a Turing machine program of at least
, i.e. they require a Turing machine program of at least 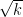 bits in length to construct. (Nothing special about
bits in length to construct. (Nothing special about 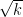 here; anything between
here; anything between 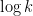 and k, basically, would suffice here.) Let S be the union of all the
and k, basically, would suffice here.) Let S be the union of all the 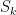 . An easy counting argument shows that S is extremely dense.
. An easy counting argument shows that S is extremely dense.
Now let A be an oracle that reports membership in S in unit time. Then we now have a very quick way to probabilistically exhibit k-digit elements of S; just select k-digit numbers at random and test them using A until we get a hit.
On the other hand, I want to say that it is not possible to find an deterministic algorithm that can locate a k-digit element of S in time polynomial in k, even with the use of oracle A. Heuristically, the reason for this is that any such algorithm will, in the course of its execution, only encounter integers with a Kolmogorov complexity of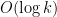 (since that integer can be described by running a O(1)-length Turing machine for a time polynomial in k (and this time can be stored as a
(since that integer can be described by running a O(1)-length Turing machine for a time polynomial in k (and this time can be stored as a 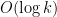 -bit integer)). In particular, one expects that the oracle A will return a negative answer to any query that that algorithm asks for, and so the oracle is effectively useless; as such, it should not be able to reach any high-complexity number, such as an element of S.
-bit integer)). In particular, one expects that the oracle A will return a negative answer to any query that that algorithm asks for, and so the oracle is effectively useless; as such, it should not be able to reach any high-complexity number, such as an element of S.
As stated, the argument doesn’t quite work, because integers of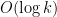 complexity can respond positively to A if they are very short (specifically, if they have
complexity can respond positively to A if they are very short (specifically, if they have  digits). Because of this, the oracle A is not completely useless, and can in principle provide new information to the algorithm that may let it reach numbers that previously had too high complexity to be reached. But it seems to me that there should be some way of fixing the above construction to avoid this problem (perhaps by constructing the
digits). Because of this, the oracle A is not completely useless, and can in principle provide new information to the algorithm that may let it reach numbers that previously had too high complexity to be reached. But it seems to me that there should be some way of fixing the above construction to avoid this problem (perhaps by constructing the 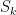 in some inductive manner?)
in some inductive manner?)
I also don’t know what the status of P=BPP is in this oracle model. After fixing the above oracle, an obvious next step would be to try to modify it further so that P=BPP is true (or false), to rule out the possibility of using P=BPP in a soft manner (as was suggested previously) to solve the problem conditionally.
It seems that the above arguments also suggest that soft methods only allow one to find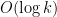 -digit primes in polynomial time, or equivalently to find k-digit primes in exponential primes. Thus finding superlogarithmic-digit primes in polynomial times, or k-digit primes in subexponential primes, would be a significant advance, and must necessarily use something nontrivial about primes beyond their density and testability.
-digit primes in polynomial time, or equivalently to find k-digit primes in exponential primes. Thus finding superlogarithmic-digit primes in polynomial times, or k-digit primes in subexponential primes, would be a significant advance, and must necessarily use something nontrivial about primes beyond their density and testability.
Perhaps it could also be possible to show that reducing the amount of random bits required to find a prime cannot be made o(k) by similarly soft methods.
Comment by Terence Tao — August 3, 2009 @ 11:43 am |
The question seems to be whether the ability to generate short (length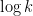 ) somewhat-random strings gives you the ability to easily generate long (length k) somewhat-random strings, where a string is somewhat random if it has Kolmogorov complexity at least the square root of its length. Playing Devil’s Advocate, one might guess that this is possible, simply by running through all strings of length
) somewhat-random strings gives you the ability to easily generate long (length k) somewhat-random strings, where a string is somewhat random if it has Kolmogorov complexity at least the square root of its length. Playing Devil’s Advocate, one might guess that this is possible, simply by running through all strings of length 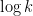 , and consecutively outputting those which are somewhat random. Not that I see how to prove this works.
, and consecutively outputting those which are somewhat random. Not that I see how to prove this works.
How might one imagine modifying $S$ to avoid this kind of difficulty?
Comment by Michael Nielsen — August 3, 2009 @ 6:30 pm |
With access to an oracle of Kolmogorov random strings, one can deterministically construct an n-bit Kolmogorov random string in time polynomial in n.
See for example Lemma 42 in this paper
Click to access KT.pdf
The idea is quite simple: one keeps adding O(log n) bit suffixes y to the (inductively) constructed random string z. One can argue that there is always a suffix y such that zy is random, as by counting many y are random relative to z and by symmetry of information
C(zy) >= C(z)+C(y|z) – 2log|zy|.
Comment by Troy Lee — August 4, 2009 @ 4:28 pm |
I am curious to what extent we have a genuine derandomization question or the problem is mainly a problem in number theory which is stated in terms of computational complexity (which is by itself welcome). To try to clarify what I mean here are a few analogs:
a) The possibility to find a detrministic polynomial algorithm for primality is a fairly clear prediction of computational complexity insights in the direction P=BPP.
On the other hand here are some problems where computational complexity is just a way to formulate a problem in NT:
b) Given an oracle which gives in unit time the nth digit of pi find a polynomial algorithm in k to find a digit ‘9’ in a place between 10^k and 10^{k+1}.
c) Given an oracle for factoring in unit time find a polynomial time algorithm in k to find a square free number with k digits with odd number of prime factors.
I think our problem is more similar to b) (and even more to c)) than to a); One difference is that primality is polynomial in the number of digits, but I am not sure if this property or some particular aspects of our problem are enough to make a difference in this respect.
Comment by Gil Kalai — August 4, 2009 @ 5:00 pm |
I think that the whole point of this oracle construction was showing that any algorithm for generating primes must use some special properties of the primes and not just their density. Question b would be similar and would need to use some special properties of the language “the n’th digit of pi is 9” in time that is polynomial in log(n). And so would question c (although in this case, I don’t see why we don’t just take the product of k/logk primes, each about logk bits long.)
Comment by algorithmicgametheory — August 4, 2009 @ 7:58 pm |
Regarding c) right, we can reformulate the question and ask to find two consecutive numbers with this property…
Comment by Gil — August 8, 2009 @ 10:01 am |
I think that this proof can be fixed by choosing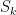 to the set of strings that have high Kolmogorov complexity even relative to the oracle containing
to the set of strings that have high Kolmogorov complexity even relative to the oracle containing 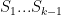 (i.e. that a TM with access to this oracle still needs large description). This way any oracle queries of length strictly less than n do not help in finding strings of length n.
(i.e. that a TM with access to this oracle still needs large description). This way any oracle queries of length strictly less than n do not help in finding strings of length n.
Comment by algorithmicgametheory — August 4, 2009 @ 7:49 pm |
I think this does indeed fix the argument, thanks! I wrote it up at
http://michaelnielsen.org/polymath1/index.php?title=Oracle_counterexample_to_finding_pseudoprimes
So, to solve the problem, we either need to use something special about primes, or to use an argument that is not relativisable.
I wonder if one can modify the oracle to obey or not obey P=BPP; this would show that P=BPP is not directly relevant to the problem.
Comment by Terence Tao — August 4, 2009 @ 10:00 pm |
Five years ago, Ralf Stephan from the OEIS put together 117 conjectures in this document: http://arxiv.org/PS_cache/math/pdf/0409/0409509v4.pdf
Most of them were elementary and were proved by a group effort, but some weren’t.
His Conjecture 28 was that, for any n>4, the n-bit binary numbers with four non-zero bits include a prime number.
Comment by Michael Peake — August 3, 2009 @ 1:20 pm |
This seems like a plausible conjecture; setting the first and final bit to equal 1 (to make the number odd) one has about k^2 k-bit numbers of this type, each of which one expects to have about a 1/k chance of being prime, so the failure rate should be exponentially small in k, and so by Borel-Cantelli one expects only a finite number of k for which the conjecture fails. But this is only a heuristic argument; there could be a very unlikely but (to our current knowledge) mathematically possible “conspiracy” in which all of these numbers defy the odds and end up being composite.
This is close to the existing strategy of trying to show that any interval of size (say) of k-digit integers contains a prime (cf. Cramer’s conjecture). I’m not sure whether using sets such as sparse sums of powers of two are better than intervals, though. It’s true that there are some specialised primality tests for such numbers (e.g. special number field sieve), but I don’t see how to use these (and they would also be available for, say, a shortish interval of numbers near
of k-digit integers contains a prime (cf. Cramer’s conjecture). I’m not sure whether using sets such as sparse sums of powers of two are better than intervals, though. It’s true that there are some specialised primality tests for such numbers (e.g. special number field sieve), but I don’t see how to use these (and they would also be available for, say, a shortish interval of numbers near 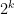 ).
).
Comment by Terence Tao — August 3, 2009 @ 3:08 pm |
Dear Michael,
Regarding conjecture 28 which has 4 binary bits the smallest bit is 1. If two of the other bits are ODD and one EVEN bit plus 1 it would be multiple of 3.
And given a k-bit binary width odd number irregardless of number of bits the probability of it to be composite is:
(1+2+..+k+1) / LCM(1,2,..,k).
This is the combined probabilities of smaller primes that might divide that number. They work synergetically together. For instance the probability of any prime as a factor is 1 / phi(p), but this is when a particular prime is independently analyze not in combination of other primes. But together these small primes in combination, now if you analyse the probability of a particular prime is 1 / J(p). I have to describe this new function. This new function is simply the order of Mersenne in which this prime divides. The relationship of this prime to this Mersenne is simply the J(p) = J(M_p) = order of M_p which is about the log of M_p. This is actually the specialized form of euler function phi and carmichael function and it is simply the Fermat’s Little Theorem in binary form.
So the above probability’s numerator is the sum of all these Mersennes logs. Using it this way we don’t need to know what prime/s divides the mersenne concern or the probable prime/s that might divide the number but knowing that their combine probabilities (synergic) is simply express by their mersennne associates. Let me elaborate further, the probabilities :
1/1 by 1, 1/2 by 3, 1/3 by 7, 1/4 by 5,,,2/x by the M_x/2.
If you look into the probability of 7 is 1/3 it should be 1/6 or 1 /phi(7) is 6. But because of probability of 1/2 by 3 affected all probabilities.
This is the same reason why carmichael function doesn’t use multiplication in ‘combining’ totient functions of products. e.g phi(a * b) = phi(a) * phi(b), while carmichael function let’s call it Y.
Y(a * b) = LCM(a,b). This J function also uses LCM i.e J(a * b) = LCM(a,b). BUT with proviso that only using with all other primes concerns. The major difference of J function to both phi and Y functions is that J function can have ODD values, e.g. the order of Mersenne 11 is 11 and the associated primes are 23 and 89.
Comment by jaime montuerto — August 5, 2009 @ 8:07 am |
I’ve reorganised the wiki page to specify some specific conjectures that are emerging from this project:
* Strong conjecture: one can find a -bit prime deterministically in polynomial time.
-bit prime deterministically in polynomial time. -bit prime probabilistically using
-bit prime probabilistically using 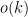 random bits in polynomial time.
random bits in polynomial time. -bit prime deterministically in
-bit prime deterministically in  time, or equivalently one can find a
time, or equivalently one can find a  -bit prime deterministically in polynomial time.
-bit prime deterministically in polynomial time.
* Semi-weak conjecture: One can find a
* Weak conjecture: One can find a
One can also pose any of these conjectures in the presence of a factoring oracle (or under the closely related assumption that factoring is in P), thus leading to six conjectures, of which “weak conjecture with factoring” is the easiest.
I’ve also added a section on “how could the conjecture(s) fail?”. Basically, several weird things have to happen in order for the any of the conjectures to fail, in particular all large constructible numbers have to be composite (or smooth, if factoring is allowed), and in fact sit inside large intervals of composite or smooth numbers. Also, no pseudorandom number generation is allowed. One also has the peculiar situation in which testing any given number for primality is in P, but testing an interval for the existence of primes cannot be in P (though it lies in NP).
I’ve also realised that most of the facts in number theory we know about primes are only average-case information rather than worst-case information, even with such strong conjectures as GRH, GUE, prime tuples, etc: they say a fair a bit about the distribution of primes near generic integers, but are not so effective for the “worst” integers, e.g. the ones inside the largest prime gaps. The whole problem here is that deterministic polynomial time algorithms can only reach the “constructible” k-digit integers, which (by a trivial counting argument) are an extremely sparse subset of the set of all k-digit integers (being only polynomial size in k rather than exponential). As such, there could be a massive “conspiracy” to place all the constructible numbers inside the rare set of “worst-case” integers in the statements of average-case number theory results, thus rendering such results useless. This conspiracy is incredibly unlikely, but we are now in the familiar position of not being able to disprove such a conspiracy. But if it were possible to somehow “amplify” the failure of average-case results for the constructible numbers to imply failure of the average-case results for a much larger set of numbers, then one might be able to get somewhere. For instance, pseudorandom number generators would accomplish this, but of course we would like to use less strong conjectures for this purpose. One reason I like Tim Gowers additive combinatorial approach (#18) is because it seems to be trying to achieve precisely this sort of amplification. (But the numerology of the approach will certainly have to be checked to ensure that it looks viable.)
Comment by Terence Tao — August 3, 2009 @ 3:01 pm |
I have a heuristic argument that “average case” results about the primes, such as that coming from GRH, GUE, the prime tuples conjecture, and the distribution of prime gaps, are effectively useless for this problem. The argument goes as follows: suppose one replaces the set of k-digit primes with the set of k-digit “generic” primes, defined as those k-digit primes with Kolmogorov complexity at least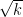 (say). Counting arguments show that almost all primes are generic, and thus any average-case statement that is true for primes, is also true for generic primes (unless the size of the exceptional set in the average case statement is extremely small). On the other hand, it is not possible to deterministically locate a k-digit generic prime in polynomial time, because any number obtained in such a fashion has a Kolmogorov complexity of O(log k).
(say). Counting arguments show that almost all primes are generic, and thus any average-case statement that is true for primes, is also true for generic primes (unless the size of the exceptional set in the average case statement is extremely small). On the other hand, it is not possible to deterministically locate a k-digit generic prime in polynomial time, because any number obtained in such a fashion has a Kolmogorov complexity of O(log k).
So one is going to have to rely on worst-case number-theory results rather than average-case ones. But now things are much weaker. For instance, the average prime gap between k-digit primes is of size O(k), but the best known upper bound on the largest prime gap is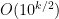 even assuming GRH. The one number-theoretic conjecture I know of (besides Cramer’s conjecture) which has significant worst-case content is the ABC conjecture, but unfortunately it seems the numbers we are dealing with are not quite smooth enough for this conjecture to be relevant…
even assuming GRH. The one number-theoretic conjecture I know of (besides Cramer’s conjecture) which has significant worst-case content is the ABC conjecture, but unfortunately it seems the numbers we are dealing with are not quite smooth enough for this conjecture to be relevant…
Comment by Terence Tao — August 4, 2009 @ 1:13 am |
In a similar light it is worth observing that most analytic results about existence of primes give more than one prime wherever they are looked for, even if they are often stated as simply existence results. E.g., universal gaps between primes are obtained by showing that pi(x+y)-pi(x) grows as a function of y, for suitable y=y(x), and even the theorem of Linnik on the smallest prime in an arithmetic progression actually finds an explicit lower bound for the number of primes in such a progression, and selects a suitably limit beyond which the main term dominates the error term. Even the Goldston-Pintz-Yildirim result has this feature. So, as in Terry’s comment, any such result is likely to hold also for “generic” primes in the sense he describes.
Comment by Emmanuel Kowalski — August 4, 2009 @ 9:10 pm |
Hmm, that’s a little discouraging. On the other hand, things seem to get better with a factoring oracle. One cannot simply now delete the non-generic primes, because one now has to supply a (non-existent) factoring of such non-generic primes into smaller integers, so the previous objections don’t obviously seem to apply.
On a slightly unrelated note, here is another proposal to find k-digit primes in exp(o(k)) time. There is a famous result of Friedlander and Iwaniec that there are infinitely many primes of the form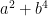 , and in fact for k large enough there exists a k-digit prime of this form. The number of k-digit numbers of this form is about
, and in fact for k large enough there exists a k-digit prime of this form. The number of k-digit numbers of this form is about 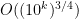 , so searching through this set beats the totally trivial bound of
, so searching through this set beats the totally trivial bound of 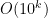 . Heath-Brown showed a similar result for numbers of the form
. Heath-Brown showed a similar result for numbers of the form 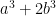 , which is a little thinner at
, which is a little thinner at 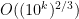 . So far, this doesn’t beat the algorithm of
. So far, this doesn’t beat the algorithm of 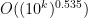 coming from Harman’s bound on prime gaps (see comment #9) but perhaps it is possible to detect primes in even thinner sets? If we can find primes in explicit sets of size
coming from Harman’s bound on prime gaps (see comment #9) but perhaps it is possible to detect primes in even thinner sets? If we can find primes in explicit sets of size 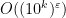 for arbitrarily small
for arbitrarily small  then we have resolved the weak (and semi-weak) conjecture.
then we have resolved the weak (and semi-weak) conjecture.
Comment by Terence Tao — August 4, 2009 @ 11:43 pm |
Heath-Brown’s result is still the one with the sparsest set of primes, as far as I know. Of course, conjectures on primes represented by irreducible polynomials of arbitrary degree would give the desired result. But that seems likely to be as hard or harder to prove than the Hardy-Littlewood conjecture (which is somewhat analogue but for reducible polynomials).
Comment by Emmanuel Kowalski — August 5, 2009 @ 1:31 am |
OK. I wonder if it would be too ambitious to try to push beyond Heath-Brown, or at least to identify some reasonable polynomial forms that were sparse but had some chance of breaking the parity barrier due to their special structure. Harold Helfgott managed to break the parity barrier for other cubic forms as well, but this presumably doesn’t lead to an increased density. (I know for sure that my results with Ben Green and Tamar Ziegler on arithmetic or polynomial progressions in primes don’t do this; they all have at least one global average in them, rather than averaging on sparse sets.)
It does seem though that (a sufficiently quantitative version of) Schinzel’s hypothesis H would establish the weak and semi-weak conjectures, by your comments, so I can add to the list of impossibly difficult conjectures which would imply some progress on this problem :-)
Comment by Terence Tao — August 5, 2009 @ 1:52 am |
This is a little off-the-cuff, so apologies in advance.
To get intuition, I was thinking about possible relaxations of the problem for which one could get partial results. For example, what about the set of numbers n which do not have prime factors smaller than n^{1/3} or polylog(n)? I’m not sure if we have efficient deterministic membership checkers for these sets, but in any case, it might be interesting to think about getting a deterministic algorithm to generate elements of such sets lying in a given interval.
Comment by Arnab Bhattacharyya — August 5, 2009 @ 2:45 am |
Can you please assist me with some background questions (probably I should have known the answers)(I did find some meterial on the internet but it is probably partial.)
1) Regarding Cramer conjecture: I recall that it is easy to demonstrate a gap of size (log n)/log log n by looking at a sequence n!+2,…,n!+n. are the longer gaps known (explicitely or not explicitly)
One direction that I find interesting would be to show that certain low-complexity devices cannot give us a way to obtain primes, and cannot even give us even a “richer in primes” environment compared to all natural numbers. Although I do not know how to define “low complexity devices”. I saw some material on primes as values of polynomials http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html (In particular, there is a result of Goldbach that there is no polynomial that always give you primes.) There are (I suppose famous) conjectures extending Direchlet’s theorem about infinitely many primes as values of polynomials (Bouniakowsky Conjecture).
2) Are there results of conjectures asserting that the density of primes values of polynomials(in one or more variables) is vanishing? (or even that there are at most n/logn primes <= n.)
(The n!+2,…n!+n gap construction extends easily to polynomials.)
3) (Most embarassing) What are the easiest ways to show that the density of primes on arithmetic progression is zero (reverse Direchlet sort of), and do they extend to polynomials?
Comment by Gil Kalai — August 5, 2009 @ 8:18 am |
Dear Gil,
A nice survey on prime gaps is Sound’s article at http://arxiv.org/abs/math/0605696 . The longest prime gap known between primes of size n has the somewhat amusing magnitude of , a result of Rankin.
, a result of Rankin.
Sieve theory can provide upper bounds on the number of primes in nice sets such as polynomial sequences which are only off by a constant factor from the expected count. In particular, the asymptotic density of primes of size n in a polynomial sequence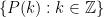 will be
will be 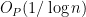 , with the implied constant depending on the polynomial P. Schintzel’s hypothesis H asserts that any polynomial P will capture infinitely many primes unless there is an obvious obstruction. By “obvious obstruction” I mean either (a) a modulus q such that P(k) is not coprime to q for all but finitely many k, (b) P(k) is negative for all but finitely many k, or (c) P factors into polynomials of lower degree. These are pretty much the only ways known to stop a sequence from containing any primes.
, with the implied constant depending on the polynomial P. Schintzel’s hypothesis H asserts that any polynomial P will capture infinitely many primes unless there is an obvious obstruction. By “obvious obstruction” I mean either (a) a modulus q such that P(k) is not coprime to q for all but finitely many k, (b) P(k) is negative for all but finitely many k, or (c) P factors into polynomials of lower degree. These are pretty much the only ways known to stop a sequence from containing any primes.
Comment by Terence Tao — August 5, 2009 @ 2:37 pm |
I was trying to look at the basic properties of primes to see how difficult it is to get integers with subsets of these properties.
The first type of properties that primes have is that they are not divisible by 2, not divisible by 3, etc. It is trivial to find an n-bit number that satisfies any given one of these conditions. How about satisfying a polynomial number of these? I.e. given a sequence of integers and a desired bit-length $n$, output an n-bit number that is not divisible by any of the
and a desired bit-length $n$, output an n-bit number that is not divisible by any of the  ‘s. (This should be done in time polynomial in the input size and in n.) This problem still seems easy since we just need to multiply a sufficient number of prime numbers that are not factors of any of the
‘s. (This should be done in time polynomial in the input size and in n.) This problem still seems easy since we just need to multiply a sufficient number of prime numbers that are not factors of any of the  ‘s, and such exist, each of length O(log n). However slight variants of this problem already seem to require something more:
‘s, and such exist, each of length O(log n). However slight variants of this problem already seem to require something more:
Problem 1: given m integers , with
, with  for all i, and a desired length $n$, output an n-bit number x such that neither x nor x+1 is divisible by any of the
for all i, and a desired length $n$, output an n-bit number x such that neither x nor x+1 is divisible by any of the  ‘s.
‘s.
Another class of properties that primes have (and are used in primality tests) is Fermat’s little theorem. While these tests don’t exactly characterize the primes (they also capture pseudo-primes), they have the advantage that (assuming ERH) only a polynomial number of them need to be checked. However it is not clear to me how to generate numbers that pass even a single such test:
Problem 2: Find an n-bit integer x such that .
.
Comment by Noam — August 5, 2009 @ 9:13 am |
Dear Noam,
In the above congruence if x is prime it will divide M_x-1(Mersenne whose order is x-1). I don’t know about its number of bits, but there is set of possible candidates (there’s more about this).
In general given a number an odd n, these conditions hold:
Say j = n – 1 = (j1 * j2 * j3,.., * ji), we get all its factor, say it has m factors. If we get the set of its Gauss Sum = m * (m+1) / 2, this will be the number of potential mersennes order that is associates of n. So we will have a set of Mersennes {M_j1,,M_j1j2,,..} m number Mersennes.
One of the three conditions should happen:
1) n | M_j, one of these Mersenne is a multiple of n AND none of the associated primes of any Mersenne divides n.
2) no Mersennes in the list is multiple of n AND two of the smaller mersennes associates primes divides n.
3) n | M_j one of the Mersenne is a multiple of n AND two of the primes of the Mersennes divides n.
The first condition n is Prime, the second n is composite and condition 3, n is carmichael number.
Let’s look at n = 341.
So j = 340 = (2 * 2 * 5 * 17), get all the combinations of Mersennes.
Mset => {M2, M4, M5, M10, M20, M17, M34, M68, M85, M170, M340}
I don’t know all the associated primes of all these mersennes, but I know these M2 => 3, M4 => 5, M5 = 31 => itself, M10 => 11, M20 => 41, M17 => itself, etc..
Now condition 1: 341 | M340, and condition 3) M5 = 31 | 341 are met so 341 is a carmichael number.
Gil Kalai mentioned Boniakovsky he discovered the congruence:
2^phi(n) congruent to 1 mod n.
Also the relationship is this J(n) | n – 1 and J(n) | phi(n). Where J(n) is a function which is the Fermat’s Little Theorem applied on odd binary numbers. If we changed the congruence above by Boniakovsky into
2^J(n) congruent 1 mod n, its obvious from here that the Mersenne whose order is J(n) is the multiple on n.
Comment by jaime montuerto — August 5, 2009 @ 12:50 pm |
I have to add about the function J(n) | n – 1, only if n is prime or pseudoprime.
Comment by jaime montuerto — August 5, 2009 @ 1:08 pm |
These are nice toy problems. For problem 1 (assuming all the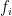 prime for simplicity), the Chinese remainder theorem can be used to solve the problem as long as the product of all the
prime for simplicity), the Chinese remainder theorem can be used to solve the problem as long as the product of all the 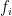 is less than
is less than 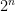 .
.
Another strategy is to pick an n-bit number (e.g.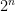 ) and advance it by 1, checking each of the numbers in turn for the desired property. Sieve theory techniques can bound the length one has to search before one is guaranteed a hit. For instance, if all the
) and advance it by 1, checking each of the numbers in turn for the desired property. Sieve theory techniques can bound the length one has to search before one is guaranteed a hit. For instance, if all the 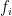 have magnitude greater than m, then searching 2m+1 consecutive integers will suffice since each modulus
have magnitude greater than m, then searching 2m+1 consecutive integers will suffice since each modulus 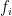 can only knock at most two of the candidates.
can only knock at most two of the candidates.
The difficulty with Problem 2 seems to be that there is no apparent relationship of much use between the residues as x varies, nor is there an obvious way to “control” this residue other than to control the prime factorisation of x (in which case one is done anyway). Given how rare pseudoprimes are compared to the primes, I would imagine this problem is essentially as difficult as the original problem.
as x varies, nor is there an obvious way to “control” this residue other than to control the prime factorisation of x (in which case one is done anyway). Given how rare pseudoprimes are compared to the primes, I would imagine this problem is essentially as difficult as the original problem.
Comment by Terence Tao — August 5, 2009 @ 2:58 pm |
Dear Terry,
Last night I made a pen and paper algolrithm I am talking about. I picked Mersenne100 because it’s the first 3 digit and 100 is a nice decimal number. Here are the associated primes:
101, 8101, 268501.
I also cheated to check that there really are primes in googles. All the talk so far strengthen and supports my algol. Picking Mersenne 100 is by whim, it could have been any other Mersennes but inline with your project slowing building up all the smaller Mersennes will help up the test later for sieving out potential composite. This Mersenne algol is similar to euclid prime production and has the non-trivial geometric series Tim Gower pointed out on Paul Erdos results. Mersennes has the other property other have not pointed out. It has the property of Fibonacci sequennce, I really don’t know the impact of Fibonacci sequence. Together the near geometric progression and Fibonacci like sequencing this has a good mix of properties your looking for.
Besides it is backed up by powerful theorems and conjectures. Fermat’s Little Theorem, Euler function, Carmichael function, Poclington’s theorem, Legendre’s theorem on Mersenne, Wilson’s primes, Wagstaff primes, Riesel composite numbers, Euclid prime production, Gause logarithmic prime connection, works of Maurer highlights aspects of this, Carl Pomerance is studying a logarithnmic function that has game theory aspect of it, I believe it has connection with my J function, Cramer’s conjecture and Bertrands Postulate I see them as two side of a coin in coining to my algol.
Comment by jaime montuerto — August 7, 2009 @ 7:49 am |
I am not a number theorist, but doesn’t a good algorithm already exist in the form of Maurer’s method[1] for generating provable prime numbers. Maurer seeks to generate random primes for cryptographic use and therefore uses a RNG in the algorithm, but this seems (to this naive reader) easy to replace.
[1] http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.26.2151
Comment by Damien Miller — August 6, 2009 @ 1:22 am |
As far as I can see, the analysis of the algorithm only provides an expected running time which is polynomial, no worse-case analysis (which is what the current project is looking for). Moreover, the running time is computed by using 1/log(2^k) as the probability that an integer is prime, and using this to compute how many iterations are required of a primality test. So this doesn’t seem to be a mathematically rigorous solution.
Comment by Emmanuel Kowalski — August 6, 2009 @ 3:35 pm |
Here is an article on Maurer’s method:
Click to access ProvablePrimes.pdf
It gives an expected running time of
O(k^4/log(k). See section 5.1 of the above paper.
Comment by Kristal Cantwell — August 6, 2009 @ 3:55 am |
Here is a link to an article by Maurer about generating prime numbers:
Fast generation of prime numbers and secure public-key cryptographic parameters at:
http://eprints.kfupm.edu.sa/40655/
Comment by Kristal Cantwell — August 6, 2009 @ 4:01 am |
Here’s a very simple strategy based on a factoring oracle and Euclid’s proof of the infinitude of primes (which is similar to Klas’s earlier suggestion and the W-trick). It isn’t immediately clear to me how to do the time analysis (maybe it is to someone else?):
1) Multiply the first ln(k) primes together and call this A.
2) Factor A. If there is a k-digit prime divisor your done. Otherwise multiply A by all of the prime factors of A+1.
3) Repeat until you find a k-digit prime.
The general idea is that if A doesn’t have a large prime factor, it must have a lot of small prime factors. Since every prime divisor of A+1 is distinct from the prime divisors of A, the list of primes you multiply together to get (the next) A should grow very quickly. I imagine this gives some kind of gain over a brute force search?
Comment by Anonymous — August 7, 2009 @ 1:11 am |
There are papers on the prime factors of products of consecutive integers; for instance Balog and Wooley show that, for any fixed positive , one can find arbitrarily long strings (starting at
, one can find arbitrarily long strings (starting at  ) consisting of
) consisting of 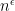 -smooth integers. The length of the string grows like
-smooth integers. The length of the string grows like  in their construction, and they observe that
in their construction, and they observe that  or $\latex (\log n)^2$ is likely to not be possible heuristically, which — if correct — would give a solution to the problem under the assumption that factoring is possible quickly.
or $\latex (\log n)^2$ is likely to not be possible heuristically, which — if correct — would give a solution to the problem under the assumption that factoring is possible quickly.
The paper is “On strings of consecutive integers with no large prime factors”, J. Austral. Math. Soc. Ser. A 64 (1998), no. 2, 266–276 (the length of the string grows like )…
)…
See here.
Comment by Emmanuel Kowalski — August 7, 2009 @ 3:19 pm |
I’m sure this algorithm would work well on the average (though I would not be able to prove this), and several other algorithms proposed here also have convincing heuristic arguments that they should succeed for most inputs k. But for the purposes of this particular project, it is the worst-case scenario which one needs to control – how bad would things get if Murphy’s law held and the primes were maximally unfriendly towards one’s algorithm?
The basic issue here is that at the k^th step of this algorithm, one has only excluded poly(k) primes from consideration. In the worst-case scenario, the next number generated by this algorithm could be generated by the first prime that has not already been excluded, which would be only of polynomial size in k rather than exponential. Admittedly, this is an unlikely scenario, but the trick is to figure out how to rule it out completely.
Currently, all of our algorithms, after k steps, are only capable of producing a prime of size as low as k^2 (modulo lower order terms) in the worst case (and this requires GRH). Even getting a prime of size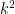 or greater in k steps unconditionally would be a breakthrough, I think.
or greater in k steps unconditionally would be a breakthrough, I think.
Comment by Terence Tao — August 7, 2009 @ 3:36 pm |
I thought I would mention an idea that occurred to me this past week, though maybe it is already implicit in some of the discussion on “soft methods” for finding large primes (I have been away for three days, so have not had the chance to read much about progress on the project).
Assuming that factoring is “easy”, I want to show that either we can find large primes quickly (say sub-exponential in k), or else such number theory conjectures as the “No Siegel Zeros” conjecture are true (and perhaps strong forms of the “Chebotarev’s density theorem”, and many other such conjectures, can be assumed to hold by similar ideas). The hope would be that having such a theorem be true can be used to boost the effectiveness of other potential methods to find large prime numbers (for one thing, if “No Siegel Zeros” holds, then we know that primes are “well-distributed in arithmetic progressions”, a powerful ingredient in potential sieve method approaches to locating primes).
My first suggestion is that if there are infinitely many (sufficiently bad) Seigel zeros, then we know, say, that there are infinitely many moduli M for which all the Jacobi symbols
(M/q) = -1, for primes $q < B := \exp(\sqrt{\log M})$, gcd(q,M)=1.
This means that the Jacobi symbol can be used to “approximate the Mobius function mu'', and since good bounds on “character sums'' are much easier to come by than analogous sums involving mu, it is can be used to improve the quality of results produced by sieve methods to find primes; indeed, Roger Heath-Brown used this idea to show that if there just enough Seigel zeros, then the Twin Prime Conjecture holds. Perhaps there are other important instances of the Hardy-Littlewood conjecture that can be attacked in a similar way.
My second suggestion is incomplete, but more direct: suppose that Siegel zeros exist (there are infinitely many of them, say). Then consider the form
$$
f(x,y) = x^2 – M y^2,
$$
where M is the modulus of a Siegel zero; and consider, for example, f(1,1) = 1 – M. This number cannot be divisible by any small prime q < B, else (M/q)= (1/q) = +1. So, all prime factors of f(1,1) lie in $[B,M^3]$, and therefore if factoring is “easy'', we will have found a large prime!
But how do we locate such a modulus M, assuming they exist? I'm not sure, but it seems like maybe we could use the fact that we have lots of different values of the form f to play around with — we would just need to choose xy coprime to M. Of course we could also try to build a sieve somehow, as numbers M satisfying (M/q)=-1 for primes q < B are quite rare!
Comment by Anonymous — August 9, 2009 @ 12:08 am |
[…] primes” as the massively collaborative research project Polymath4, and now supercedes the proposal thread for this project as the official “research” thread for this project, which has now become rather […]
Pingback by (Research thread II) Deterministic way to find primes « The polymath blog — August 9, 2009 @ 3:58 am |
This preliminary research thread (which was getting quite lengthy) has now been superseded by the new research thread at
All new research comments should now be made at that thread. Participants are of course welcome to summarise, review, or otherwise carry over existing comments from this thread at the next one; this would be a good time to recap any progress that has not been sufficiently emphasised already.
Comment by Terence Tao — August 9, 2009 @ 4:10 am |
[…] The exciting new Polymath Project, to find (under some number-theoretic assumption) a deterministic polynomial-time algorithm for […]
Pingback by Shtetl-Optimized » Blog Archive » Ask me (almost) anything — May 6, 2013 @ 2:31 pm |