This post will be somewhat abridged due to my traveling schedule.
The previous research thread for the “finding primes” project is now getting quite full, so I am opening up a fresh thread to continue the project.
Currently we are up against the “square root barrier”: the fastest time we know of to find a k-digit prime is about (up to
factors), even in the presence of a factoring oracle (though, thanks to a method of Odlyzko, we no longer need the Riemann hypothesis). We also have a “generic prime” razor that has eliminated (or severely limited) a number of potential approaches.
One promising approach, though, proceeds by transforming the “finding primes” problem into a “counting primes” problem. If we can compute prime counting function in substantially less than
time, then we have beaten the square root barrier.
Currently we have a way to compute the parity (least significant bit) of in time
, and there is hope to improve this (especially given the progress on the toy problem of counting square-frees less than x). There are some variants that also look promising, for instance to work in polynomial extensions of finite fields (in the spirit of the AKS algorithm) and to look at residues of
in other moduli, e.g.
, though currently we can’t break the
barrier for that particular problem.
[…] https://polymathprojects.org/2009/08/09/research-thread-ii-deterministic-way-to-find-primes/ […]
Pingback by Polymath4 « Euclidean Ramsey Theory — August 28, 2009 @ 3:20 am |
I worked out a way to leverage a power savings improvement (over the hyperbola method) in computing sums of divisors, to break the square-root barrier for computing the parity of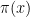 , assuming of course I haven’t made any errors. I have written a two page note on it, which can be found by going to my homepage at
, assuming of course I haven’t made any errors. I have written a two page note on it, which can be found by going to my homepage at
Click to access squarerootbarrier.pdf
(I wrote it in terms of the way I first explained how to compute parity of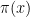 , not Terry’s cleaner version — I am sure the algorithm can be rephrased in terms of the cleaner approach.)
, not Terry’s cleaner version — I am sure the algorithm can be rephrased in terms of the cleaner approach.)
As to breaking to the square-root barrier for computing divisor sums, I think one can just use some linear approximations to curves , along with Pick’s Theorem to count lattice points in polygonal regions — if so, this would give a much more elegant approach than I wrote on before (the `crude method’). There are some issues with the approximating lines not having endpoints that are lattice points, and issues with points between the approximating lines and the curve, but I think these can perhaps be dealt with. I may write more on this in a day or two.
, along with Pick’s Theorem to count lattice points in polygonal regions — if so, this would give a much more elegant approach than I wrote on before (the `crude method’). There are some issues with the approximating lines not having endpoints that are lattice points, and issues with points between the approximating lines and the curve, but I think these can perhaps be dealt with. I may write more on this in a day or two.
Comment by Ernie Croot — August 28, 2009 @ 1:55 pm |
[[ Parity may be all we need! ]]
It occurred to me just now that computing the parity of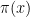 is almost sufficient to solve the “finding primes” problem by itself, without need for further bits of
is almost sufficient to solve the “finding primes” problem by itself, without need for further bits of 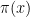 .
.
Indeed, suppose we have a parity oracle, and have somehow found an interval![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=000000&s=0&c=20201002) in which
in which  and
and  have different parity. Then for any c between a and b, the parity of \pi(c) must differ from either that of
have different parity. Then for any c between a and b, the parity of \pi(c) must differ from either that of  or that of
or that of  . So with one query to the parity oracle, we can pass to an interval of half the size in which the parities of the endpoints differ. Iterating this a logarithmic number of times, we end up at a prime.
. So with one query to the parity oracle, we can pass to an interval of half the size in which the parities of the endpoints differ. Iterating this a logarithmic number of times, we end up at a prime.
So, with a parity oracle, all we need to do to win is to find two k-digit numbers a,b in which the parities of \pi(a), \pi(b) differ. I’m stuck on how one is supposed to do precisely that deterministically (it’s trivial probabilistically, of course), but it does seem to be a reduction in difficulty in the problem…
Comment by Terence Tao — August 29, 2009 @ 5:01 am |
“(it’s trivial probabilistically, of course),”
why?
Comment by Gil Kalai — August 29, 2009 @ 9:48 am |
Huh. I thought it was obvious that the parity of pi(x) was equidistributed (i.e. approximately half of all numbers have an even number of primes less than them) but now that I think about it, I can’t get this without some conjectures on prime gaps on the level of GUE. I suppose the primes could conceivably come in pairs with small separation between them, so that one parity class overwhelms the other in size, though clearly this is not what actually happens.
Anyway, the only way things can go wrong with a parity oracle is of all the constructible k-digit numbers in the world have the same parity of pi(x), which really is bizarre but I can’t see how to rule it out yet.
Comment by Terence Tao — August 29, 2009 @ 9:52 am |
Actually, now that I think about it, for every prime p, p and p-1 have opposite pi-parity, so the probability of hitting a given pi-parity has to be at least 1/log x by the prime number theorem, so one can get two different parities in polynomial time probabilistically (but this is not so different from the probabilistic algorithm to find a prime in the first place).
Comment by Terence Tao — August 29, 2009 @ 9:53 pm |
That’s a nice idea, finding two numbers where the parity of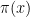 differs (though, I knew about it, and it was sort of implicit in one of the postings I wrote earlier, that if the parity of
differs (though, I knew about it, and it was sort of implicit in one of the postings I wrote earlier, that if the parity of 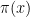 on some long interval [a,b] is odd, as provided by an oracle, then we are done). The same idea works for the
on some long interval [a,b] is odd, as provided by an oracle, then we are done). The same idea works for the ![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) approach — just find a long interval, say,
approach — just find a long interval, say, ![[a,2a]](https://s0.wp.com/latex.php?latex=%5Ba%2C2a%5D&bg=ffffff&fg=000000&s=0&c=20201002) , such that the the generating function for the primes in this interval is not divisible by a small-degree polynomial — then, some binary searching can be used to do the rest (you can just cut the interval in half, and mod the two generating functions out by the small degree polynomial, and one of these congruences must be non-zero, then iterate).
, such that the the generating function for the primes in this interval is not divisible by a small-degree polynomial — then, some binary searching can be used to do the rest (you can just cut the interval in half, and mod the two generating functions out by the small degree polynomial, and one of these congruences must be non-zero, then iterate).
The![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) approach is looking a lot more promising to me, especially since I think that the methods of breaking the square-root barrier for finding the parity of
approach is looking a lot more promising to me, especially since I think that the methods of breaking the square-root barrier for finding the parity of  can be transferred to the polynomial ring setting (I will need to look at Harald’s posting below carefully to see if this is the case). Just the other day, an idea occurred to me, and though it was wrong, it had an insight that I think might lead somewhere. The idea was this: not only can we compute the prime generating function
can be transferred to the polynomial ring setting (I will need to look at Harald’s posting below carefully to see if this is the case). Just the other day, an idea occurred to me, and though it was wrong, it had an insight that I think might lead somewhere. The idea was this: not only can we compute the prime generating function  —
— 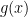 has low degree — very quickly, but we can likewise compute
has low degree — very quickly, but we can likewise compute  very quickly. THe fleeting thought that passed through my mind was that if both of these turned out to be
very quickly. THe fleeting thought that passed through my mind was that if both of these turned out to be  , then
, then  divides f(x), which is impossible for large q. Although I realized half a second later that this is nonsense, it led me to the following: not only can be compute
divides f(x), which is impossible for large q. Although I realized half a second later that this is nonsense, it led me to the following: not only can be compute  quickly, but we can compute any number of compositions
quickly, but we can compute any number of compositions  quickly, at least if the
quickly, at least if the  have very few terms (i.e. they are lacunary). It seems to me that one can somehow utilize this (as I had attempted with the `nonsense idea’), choosing the polynomials
have very few terms (i.e. they are lacunary). It seems to me that one can somehow utilize this (as I had attempted with the `nonsense idea’), choosing the polynomials 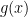 to mod out by, to gain control over an exponential explosion of roots of
to mod out by, to gain control over an exponential explosion of roots of 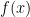 ; if so, then I can imagine that this can be used to obtain a fast algorithm (breaking the square-root barrier) to locate primes. I’ll think about it…
; if so, then I can imagine that this can be used to obtain a fast algorithm (breaking the square-root barrier) to locate primes. I’ll think about it…
I once wrote a note to Michael Filaseta (or maybe I just told it to him? can’t remember) that may have some useful ideas — I’ll have to dig it up from my computer account if it exists. As I recall, he had an algorithm to quickly determine whether certain lacunary polynomials are irreducible. Upon telling me about his method, I found a completely different approach, that worked by seeing how the ideal (2) splits in finite extensions of Z (and I have totally forgotten how the algorithm worked). By Kummer’s prime ideal factorization theorem, this is related to seeing how polynomials split in![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) — so, there may be some ideas in that note that are relevant to our problem. I’ll keep you posted if anything develops.
— so, there may be some ideas in that note that are relevant to our problem. I’ll keep you posted if anything develops.
Comment by Ernie Croot — August 30, 2009 @ 3:07 am |
Regarding our very basic problem let me point out that there are two variants:
1) (effective) find a constant A and a deterministic algorithm that find a k-digit prime wose running time is bounded above by .
.
2) (non effective) Prove that there is a deterministic time algorithm whose running time is bounded above by for some
for some  .
.
As far as I can see Cramer’s conjecture gives only a non effective algorithm (version 2).
Comment by Gil Kalai — August 29, 2009 @ 9:24 am |
Does the distinction between effective and non effective version of the problem make sense? What can we expect from complexity theoretic assumptions of hardness? (Or does the distinction extend to them.)What is the status of the existing (exponential) deterministic algorithms.
Comment by Gil Kalai — August 31, 2009 @ 6:16 am |
It seems to me that I can compute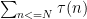 in time
in time  . The argument is similar to elementary proofs (such as the one waved at in the exercises to Chapter 3 of Vinogradov's Elements of Number Theory) of the fact that the number of points under the hyperbola equals
. The argument is similar to elementary proofs (such as the one waved at in the exercises to Chapter 3 of Vinogradov's Elements of Number Theory) of the fact that the number of points under the hyperbola equals  . Thanks to Ernie Croot for the inspiration – all mistakes below are my own.
. Thanks to Ernie Croot for the inspiration – all mistakes below are my own.
What we must do is compute in time
in time  . Assume that
. Assume that  . Assume furthermore that
. Assume furthermore that
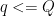 , where
, where  . Then the sum
. Then the sum
can be computed in time with an error term < 1/2.
with an error term < 1/2.
Before I prove this lemma, let me show why it is enough for attaining our goal (namely, computing with *no* error term). We know that
with *no* error term). We know that
We also know that is an integer. Thus,
is an integer. Thus, with an error term <1/2
with an error term <1/2 exactly.
exactly.
it is enough to compute
in order to compute
We now partition the range , into intervals of the form
, into intervals of the form  , where q is the denominator of a good approximation to N/x^2, that is to say, an approximation of the form
, where q is the denominator of a good approximation to N/x^2, that is to say, an approximation of the form  with an error term
with an error term 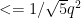 . Such good approximations are provided to us by Hurwitz's approximation theorem. Moreover, it shouldn't be hard to show that, as x varies, the q's will be fairly evenly distributed in [1,Q]. (Since Hurwitz's approximation is either one of the ends of the interval containing
. Such good approximations are provided to us by Hurwitz's approximation theorem. Moreover, it shouldn't be hard to show that, as x varies, the q's will be fairly evenly distributed in [1,Q]. (Since Hurwitz's approximation is either one of the ends of the interval containing  in the Farey series with upper bound Q/2 or the new Farey fraction produced within that interval, it is enough to show that Dirichlet's more familiar approximations have fairly evenly distributed denominators.) This means that
in the Farey series with upper bound Q/2 or the new Farey fraction produced within that interval, it is enough to show that Dirichlet's more familiar approximations have fairly evenly distributed denominators.) This means that 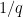 should be about
should be about  in the average.
in the average.
Thus, the number of intervals of the form x<=n<x+q into which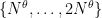 has been partitioned should be about
has been partitioned should be about  . Since the contribution of each interval to the sum
. Since the contribution of each interval to the sum  can (by Lemma 1 and the paragraph after its statement) be computed exactly in time O(\log x), we can compute the entire sum in
can (by Lemma 1 and the paragraph after its statement) be computed exactly in time O(\log x), we can compute the entire sum in 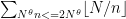 in time
in time  .
. .)
.)
(There are bits of the sum (at the end and the beginning) that belong to two truncated intervals, but those can be computed in time
We partition into O(\log N) intervals of the form
into O(\log N) intervals of the form 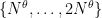 , and obtain a total running time of
, and obtain a total running time of  ,
,
as claimed.
The proof of Lemma 1 is in my next post.
Comment by H A Helfgott — August 29, 2009 @ 10:29 pm |
Harald, that’s fantastic! I will look at it very closely. It will certainly save me a lot of work trying to figure out how to use Pick’s theorem in just the right way, and in any case it or thereabouts is about the limit of how good I thought that my methods could possibly work.
or thereabouts is about the limit of how good I thought that my methods could possibly work.
Comment by Ernie Croot — August 30, 2009 @ 3:12 am |
Proof of Lemma 1.- We can write
where an integer,
an integer, 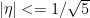 and
and 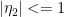 fs independent of n. Since
fs independent of n. Since 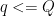 and
and  , we have
, we have
 . We also have
. We also have 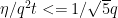 .
. . It follows that
. It follows that
Thus,
except when . That exception
. That exception (namely, when
(namely, when  is congruent mod q to
is congruent mod q to ) and we can easily find that t (and isolate it
) and we can easily find that t (and isolate it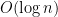 by taking the inverse of
by taking the inverse of 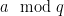 .
.
can happen for only one value of
the integer closest to
and compute its term exactly) in time
Thus, we get the sum in time
in time 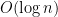 with an error term less than
with an error term less than 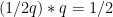 once we know the sum
once we know the sum
exactly. But this sum is equal to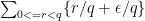 , where
, where
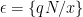 , and that sum is simply
, and that sum is simply  . Thus, we have
. Thus, we have in time
in time 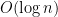 QED.
QED.
computed the sum
Comment by H A Helfgott — August 29, 2009 @ 10:49 pm |
Harald, I’ve put your argument on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=Prime_counting_function#Computing_the_parity_of_.5Cpi.28x.29
The LaTeX format on the wiki is somewhat ugly but it is readable. It is probably best to edit that page directly rather than work through the blog to clean up the argument further.
Inserting your argument into Ernie’s machine we obtain a parity oracle for pi(x) that runs in time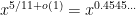 . Presumably further improvements are possible…
. Presumably further improvements are possible…
Comment by Terence Tao — August 30, 2009 @ 9:33 pm |
Obvious, unrelated and fairly empty remark: we do not really need to know pi(x) mod q – we need is a fast algorithm for determining whether q|(\pi(x+t)-\pi(x)) (a yes or no question, rather than a value mod q, though it really amounts to much the same). Since primes between x and 2x do exist, there is a q between 2 and log(x) that does not divide \pi(2x)-\pi(x). We fix that q, and start to refine the interval \pi(2x)-\pi(x)
in a binary fashion as Terry described.
Comment by H A Helfgott — August 30, 2009 @ 1:53 am |
According to Titchmarsh’s Theory of the Zeta Function, in the same paper that Vornoi obtains the error term for
error term for  he obtains a
he obtains a 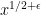 error term for
error term for  . There is actually a proof of this in Titchmarsh’s book (chapter 12), but the argument there is analytic and not combinatorial like Helfgott’s.
. There is actually a proof of this in Titchmarsh’s book (chapter 12), but the argument there is analytic and not combinatorial like Helfgott’s.
I haven’t taken a close look, but Vornoi’s 1903 (French) article is online at: http://www.digizeitschriften.de/index.php?id=loader&tx_jkDigiTools_pi1%5BIDDOC%5D=507751 .
Of course, the hope is that this could be modified to improve our current method for computing , which runs in
, which runs in  steps.
steps.
Comment by Mark Lewko — August 31, 2009 @ 7:32 am |
The link to Voronoi’s article seems to be broken; can you fix it?
Comment by H A Helfgott — August 31, 2009 @ 5:42 pm |
Sorry. There is a link to the article on the page: http://www.digizeitschriften.de/index.php?id=loader&tx_jkDigiTools_pi1%5BIDDOC%5D=507735
The article is: Voronoi, Sur un probleme du calcul des fonctions asymptotiques, J. reine angew. Math 126 (1903), 241-282
Comment by Mark Lewko — August 31, 2009 @ 6:03 pm |
Well that didn’t work… The article is supposed to be open access, but I can’t get a permanent link.
In any event, I uploaded a copy to http://lewko.wordpress.com/files/2009/08/voronoi.pdf
Comment by Mark Lewko — August 31, 2009 @ 6:13 pm |
Thanks!
Comment by H A Helfgott — August 31, 2009 @ 7:18 pm |
[…] the Polymath blog. But please be polite: read some background first, and take a look at some of the research threads to get a feel for how things work, and what’s already […]
Pingback by Michael Nielsen » Finding Primes: A Fun Subproblem — September 1, 2009 @ 9:12 pm |
I just typed up a short note this morning with an idea for how to push the F_2[x] idea forward (I did’t have to teach this morning because of a university convocation). I decided to write it up as a latex/pdf file, which can be accessed by going to
Click to access f2_idea.pdf
Comment by Ernie Croot — September 3, 2009 @ 3:31 pm |
Looks promising! Unfortunately I am swamped with my ongoing lecture series but I do like the idea of extending our current parity algorithm to a polynomial ring; polynomialisation worked for AKS, so we can hope it does so for our problem also…
Comment by Terence Tao — September 4, 2009 @ 1:53 pm |
It looks like it took a lot of time to put together those slides for your talks. They are very nicely done. I especially liked the Cosmic Distance Ladder slides.
I found a way to rewrite the generating function for the primes in![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) in terms of a sum of a small number of polynomials to high powers. That should make it much easier to attack my goal 1 in the note above, and probably also goals 2 and 3 (actually, thinking a little bit ahead, it seems to me that if goal 2 could be solved, quite likely goal 3 can be as well — the reasons are a little complicated, and maybe I will write about it later).
in terms of a sum of a small number of polynomials to high powers. That should make it much easier to attack my goal 1 in the note above, and probably also goals 2 and 3 (actually, thinking a little bit ahead, it seems to me that if goal 2 could be solved, quite likely goal 3 can be as well — the reasons are a little complicated, and maybe I will write about it later).
The new idea I had is based on the following observation: in![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) we have that
we have that
So, for example, we can write
In general, a geometric series can be written in this way using at most
can be written in this way using at most  terms — the number of terms is the number of 1’s in the base-2 expansion of
terms — the number of terms is the number of 1’s in the base-2 expansion of 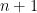 . So, replacing the
. So, replacing the  by the appropriate sums of these $x^c (1+x)^{2^k-1}$’s will only increase the number of terms in our formula for the generating function by a factor
by the appropriate sums of these $x^c (1+x)^{2^k-1}$’s will only increase the number of terms in our formula for the generating function by a factor 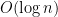 — quite small. And, of course, it gives us the flexibility of working with sparse polynomials. I haven’t tried yet to see if this makes Goal 1 tractable (perhaps now some kind of Vandermonde identity will polish it off), but it sure looks a lot easier to me now!
— quite small. And, of course, it gives us the flexibility of working with sparse polynomials. I haven’t tried yet to see if this makes Goal 1 tractable (perhaps now some kind of Vandermonde identity will polish it off), but it sure looks a lot easier to me now!
Comment by Ernie Croot — September 5, 2009 @ 2:24 pm |
And here is a further idea that builds on the new new way to write the generating function (that uses the identity), though I haven’t had time yet to try it out (maybe at the end of the week): we have reduced the generating function to a sparse sum of terms like
identity), though I haven’t had time yet to try it out (maybe at the end of the week): we have reduced the generating function to a sparse sum of terms like  , and we would like to show that as we successively replace
, and we would like to show that as we successively replace  with
with 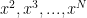 ,
, 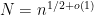 , say, that we must have at least one of these sums is non-zero
, say, that we must have at least one of these sums is non-zero  . If we just had sums of powers of
. If we just had sums of powers of  by themselves, or just sums of
by themselves, or just sums of  by themselves, then probably it would be much easier to show that one of these sums was non-zero. Well, it turns out that there is a way to combine together both of these types of sums in a nice way, and perhaps this will lead to the non-vanishing result we seek.
by themselves, then probably it would be much easier to show that one of these sums was non-zero. Well, it turns out that there is a way to combine together both of these types of sums in a nice way, and perhaps this will lead to the non-vanishing result we seek.
The idea is to use matrix tensors: first, suppose that is the matrix whose
is the matrix whose  th row is the vector
th row is the vector 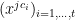 (where
(where  or so), where the
or so), where the 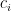 are the exponents appearing in the terms
are the exponents appearing in the terms  that we have; and let
that we have; and let  be the matrix whose
be the matrix whose  th row is the vector
th row is the vector 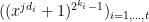 . Of course as it stands, these matrices will have 0 determinant, because some columns will be duplicated — never mind that, I know how to fix that, I think. Now, if we take the tensor
. Of course as it stands, these matrices will have 0 determinant, because some columns will be duplicated — never mind that, I know how to fix that, I think. Now, if we take the tensor 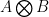 , within this
, within this 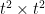 matrix will be a sub-matrix consisting of the terms
matrix will be a sub-matrix consisting of the terms 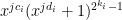 . There is some hope that this can be used to show that if the tensor is non-singular, then not all of our sums of
. There is some hope that this can be used to show that if the tensor is non-singular, then not all of our sums of  vanish
vanish  , especially since there are lots of other sub-matrices within the tensor that contain usable information about our generating function for the primes (and perhaps there is a way to relate the rank of sub-matrices of the tensor to ranks of sub-matrices of
, especially since there are lots of other sub-matrices within the tensor that contain usable information about our generating function for the primes (and perhaps there is a way to relate the rank of sub-matrices of the tensor to ranks of sub-matrices of  and
and  — I would need to brush up on my multilinear algebra).
— I would need to brush up on my multilinear algebra).
Let’s assume all this can be made to work somehow. Then how do we show that the tensor is non-singular? Well, that is where the beautiful fact that the determinant of the tensor of with
with  is a power of the determinant of
is a power of the determinant of  times a power of the determinant of
times a power of the determinant of  . In other words, if
. In other words, if  and
and  are non-singular, then so is the tensor. Now,
are non-singular, then so is the tensor. Now,  is a Vandermonde, so is well-understood, and
is a Vandermonde, so is well-understood, and  looks a lot simpler to analyze than the matrix having terms
looks a lot simpler to analyze than the matrix having terms 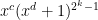 that corresponds to our prime generating function.
that corresponds to our prime generating function.
Well, all that’s just a thought… I’ll have to see if it can be made into something usable.
—-
On another front, it occurred to me how we might approach the problem of solving goal 2, of rapidly computing the generating function in![F_2[x]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) at several different powers of
at several different powers of  : what we could do is temporarily ascend out of the
: what we could do is temporarily ascend out of the ![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) context, and work in
context, and work in ![Z[x]/(g(x))](https://s0.wp.com/latex.php?latex=Z%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) instead (assume
instead (assume 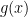 is monic). The advantage to doing this is that there is some hope of using Fourier analysis in the complex numbers, which gets around the problem of our finite field not having just the right kinds of roots of unity to apply discrete FFTs. Thinking ahead, I see that going to
is monic). The advantage to doing this is that there is some hope of using Fourier analysis in the complex numbers, which gets around the problem of our finite field not having just the right kinds of roots of unity to apply discrete FFTs. Thinking ahead, I see that going to ![Z[x]](https://s0.wp.com/latex.php?latex=Z%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) will have its own problems, however, due to the fact that when we mod out by
will have its own problems, however, due to the fact that when we mod out by 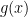 , unless
, unless 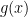 is a cyclotomic polynomial (or at least a monic polynomial with really low Mahler measure) the coefficients of the residue will be enormous, requiring very high precision to compute accurately enough for this to be viable. There may be some ways around this, though.
is a cyclotomic polynomial (or at least a monic polynomial with really low Mahler measure) the coefficients of the residue will be enormous, requiring very high precision to compute accurately enough for this to be viable. There may be some ways around this, though.
There are two other possibilities for attacking goal 2 that I know about: first, I think perhaps one can express it in terms of a matrix multiplication problem, though maybe I am mistaken — I haven’t had time to think about it. If this is the case, then there is Strassen’s algorithm, and various improvements that might work just well enough to give us a quick algorithm to locate primes (quicker than Odlyzko’s). And the other approach is one I remembered seeing in Knuth’s book “Semi-numerical Algorithms” (in my opinion, the best math and CS books that exists!) ages ago, in the section on fast multiplication of integers. As I recall, Knuth presents the standard FFT algorithm for this, but then also presents a simple recursive algorithm that requires no Fourier series at all, yet achieves a running time almost as good as what FFTs can deliver. Perhaps there are some ideas in that algorithm that can be transferred to our problem.
Comment by Ernie Croot — September 8, 2009 @ 2:26 am |
Actually, I guess that one can easily force large submatrices of a tensor to be singular (and one doesn’t need to use tensor matrices, but can just use tensor products — I don’t know why I didn’t think of that first). Still, I wonder whether the non-vanishing problem can be made into essentially a simple linear algebra problem somehow, that uses as input such data as the fact that Vandermondes are non-singular.
Comment by Ernie Croot — September 8, 2009 @ 2:10 pm |
Here I will discuss a new way that FFTs can be used to vastly speed up our algorithm for locating primes using the![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) prime generating functions: basically, we begin by applying Odlyzko’s algorithm to locate, in time
prime generating functions: basically, we begin by applying Odlyzko’s algorithm to locate, in time  , an interval
, an interval
that has at least one prime number. Recall that the![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) approach requires that we compute sums like
approach requires that we compute sums like
at the values
The trivial algorithm to do this takes time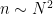 or so. Assuming that we can perform FFT’s quickly using polynomials in
or so. Assuming that we can perform FFT’s quickly using polynomials in ![F_2[x]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where 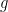 is irreducible and of degree
is irreducible and of degree 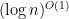 , it is easy to see how to speed this process up; and, in fact, we should get an algorithm that runs in time
, it is easy to see how to speed this process up; and, in fact, we should get an algorithm that runs in time 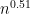 .
.
Well, it turns out that there is a somewhat less obvious way to use FFT’s to speed up the process, which seems more portable (to other variations of our prime search algorithm) than the easy-to-see application of FFTs, and which is the point of this posting: suppose that has the property that
has the property that  is the largest multiple of
is the largest multiple of  that lands in our interval
that lands in our interval 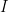 , and suppose that
, and suppose that  is near to
is near to  , but just slightly smaller. Then, we know that
, but just slightly smaller. Then, we know that
all belong to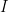 as well, at least for
as well, at least for 
to deal with. Well, these are quite similar to
and so, if the inner sum here can be evaluated at much quicker than by the trivial algorithm, then it gives us a way to speed up the
much quicker than by the trivial algorithm, then it gives us a way to speed up the ![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) algorithm.
algorithm.
There is yet another way that we can use this idea to speed up the search for primes, which involves passing to arithmetic progressions (perhaps related to one of GIl’s suggestions), and which I will write on in the next posting.
Comment by Ernie Croot — September 12, 2009 @ 10:08 pm |
I see there was a “formula does not parse”. Here it is again, rewritten slightly:
Here I will discuss a new way that FFTs can be used to vastly speed up our algorithm for locating primes using the![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) prime generating functions: basically, we begin by applying Odlyzko’s algorithm to locate, in time
prime generating functions: basically, we begin by applying Odlyzko’s algorithm to locate, in time  , an interval
, an interval
that has at least one prime number. Recall that the![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) approach requires that we compute sums like
approach requires that we compute sums like
at the values
The trivial algorithm to do this takes time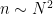 or so. Assuming that we can perform FFT’s quickly using polynomials in
or so. Assuming that we can perform FFT’s quickly using polynomials in ![F_2[x]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where 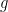 is irreducible and of degree
is irreducible and of degree 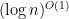 , it is easy to see how to speed this process up; and, in fact, we should get an algorithm that runs in time
, it is easy to see how to speed this process up; and, in fact, we should get an algorithm that runs in time 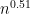 .
.
Well, it turns out that there is a somewhat less obvious way to use FFT’s to speed up the process, which seems more portable (to other variations of our prime search algorithm) than the easy-to-see application of FFTs, and which is the point of this posting: suppose that has the property that
has the property that  is the largest multiple of
is the largest multiple of  that lands in our interval
that lands in our interval 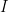 , and suppose that
, and suppose that  is near to
is near to  , but just slightly smaller. Then, we know that
, but just slightly smaller. Then, we know that
all belong to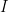 as well, at least for
as well, at least for  smaller than
smaller than 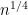 , say. If
, say. If  is somewhat smaller than
is somewhat smaller than  , then there will be a similar idea that one can use, and for the purposes of this note we will not discuss these other, slightly more complicated cases.
, then there will be a similar idea that one can use, and for the purposes of this note we will not discuss these other, slightly more complicated cases.
Let us look at the generating function for these new numbers that land in our interval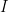 . It is given as
. It is given as
and unfortunately, the exponent here is quadratic in , making it difficult to evaluate quickly. But there is actually a way to do it using FFTs, which will allow us to quickly evaluate it at even just one value for
, making it difficult to evaluate quickly. But there is actually a way to do it using FFTs, which will allow us to quickly evaluate it at even just one value for  , which is rather surprising!
, which is rather surprising!
Here is the idea: let’s simplify matters a little, and suppose the generating function we wish to evaluate instead is
Let , where we assume
, where we assume  is a square, and let
is a square, and let
Note that we treat these as coefficients, and of course
as coefficients, and of course  as the variable. Then, it is easy to check that
as the variable. Then, it is easy to check that
So, if we can evaluate
quickly, then we can find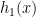 quickly. And, evaluating
quickly. And, evaluating 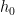 at these powers of
at these powers of  is exactly what FFTs are used for!
is exactly what FFTs are used for!
What’s more is that perhaps one can somehow use this to quickly compute the generating function for the primes that are 1 mod 4. The idea is that we will have generating functions like
to deal with. Well, these are quite similar to
and so, if the inner sum here can be evaluated at much quicker than by the trivial algorithm, then it gives us a way to speed up the
much quicker than by the trivial algorithm, then it gives us a way to speed up the ![F_2[x]](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) algorithm.
algorithm.
There is yet another way that we can use this idea to speed up the search for primes, which involves passing to arithmetic progressions (perhaps related to one of GIl’s suggestions), and which I will write on in the next posting.
Comment by Ernie Croot — September 12, 2009 @ 10:12 pm |
In case we don’t have FFTs available in the![F_2[x]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) context, I have figured out how to use Strassen’s algorithm as a substitute. I think I wrote about this before, but it took me a little thinking to see how to make it work. I have typed up a short 2-page note on how to use Strassen to evaluate the sum
context, I have figured out how to use Strassen’s algorithm as a substitute. I think I wrote about this before, but it took me a little thinking to see how to make it work. I have typed up a short 2-page note on how to use Strassen to evaluate the sum
substantially faster than time (recall that FFTs allow us to do this in time
(recall that FFTs allow us to do this in time  or so; Strassen is somewhat worse, running in time about
or so; Strassen is somewhat worse, running in time about 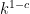 for some
for some 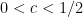 , but still it is much better than time
, but still it is much better than time  .)
.)
This note can be found by going here:
Click to access fast_strassen.pdf
I believe this means that if we combine this result with the ideas I wrote about before, we can evaluate the prime generating function for an interval![[z,z+z^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bz%2Cz%2Bz%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) in time substantially faster than
in time substantially faster than  . In other words, we have now rigorously crossed the square-root barrier in evaluating the generating function!
. In other words, we have now rigorously crossed the square-root barrier in evaluating the generating function!
Furthermore, in light of these recent improvements, we now know that the prime generating function has somewhat lower “arithmetic complexity'' that it first had seemed. This *should* mean that we no longer need to evaluate it at
in order to achieve the non-vanishing we need in order to locate primes. In fact, my preliminary calculations, based on a certain conjecture of mine (that I have not written about), implies that
should suffice. Of course, this will involve solving a stronger version of my Goal 1 in a previous note. I have some ideas on this, and will hammer away at them… hopefully I will have something to report next week.
Comment by Ernie Croot — September 14, 2009 @ 12:28 am |
Regarding the parity of pi(n) I wonder what is known about the following simple (non algorithmic) questions:
1) Consider an arithmetic progression an+b (think about a being a large integer).
We can ask what is the smallest n before we witness two members in the progression with opposite parity of pi.
The thought that the parity of pi(n) will behave rather randomly for far apart integers suggests that that n=K log(a) log log (a) or something like that would suffice (given a for all b’s).
When n is exponential in k then the gaps between terms of the arithmetic progression will become so much smaller than the gaps between primes so we should be able to find two terms with opposite signs of pi. (Actually I am not sure that even this heuristic argument can be turned to a proof. Even if it does there is a huge gap between log k and exp (k).)
2) A slightly more general question is: given a polynomial an^2 +bn +c are there two terms with opposite signs of pi? Here beside the feeling that the sign of pi will behave like a random string of +1 -1 I do not see any potential argument why the sign of pi could not be the same for all terms. Is it known?
BTW could it be easier to compute pi(n) (mod 4) rather then mod 3? (Maybe this is related to Ernie’s approach.)
Comment by Gil — September 3, 2009 @ 6:46 pm |
A couple of very qualitative observations.
The bad case on parity is where the primes in the initially chosen range (a,b) come in pairs which are ‘close together’ so that most of the integers in (a,b) come between prime pairs. So it may be worth looking at the distribution of ‘isolated primes’, or trying to identify where these may be found.
Another possible strategy to find a parity change in the first place would be to choose an interval (a,b) and extend it by not too much to find a parity change, rather than by working to reduce the length of the interval.
Comment by Mark Bennet — September 3, 2009 @ 10:01 pm |
If you tried to find a k digit prime, then a quantum computer would be able to do it in 2^c(k^1/2), c is a constant. I think. The exponent in k would become one in square root of k. In the wiki the question is asked if p = bqp how does that affect the problem. Might we get a similiar reduction from an exponent in k to an exponent in the square root of the square root of k? If p=bqp then is there some way to simulate a quantum turing machine with a turing machine? How does the time it takes to do a problem change when going from the quatum computer to its simulation?
Comment by Kristal Cantwell — September 6, 2009 @ 3:49 am |
I think a quantum computer can produce random numbers. If it could produce a k digit random number x in polynomial(k) time then we could test the numbers around this number for primes if the expected prime free gap is k and the deviation is k, which I think happens in a poisson process the testing say 100k numbers around x ought to give a probability of less than 1/3 and since the testing time is a polynomial function of k the entire process should take place in polynomial time and that would put this problem in bqp and also make the problem polynomial if p = bqp.
Comment by Kristal Cantwell — October 2, 2009 @ 4:18 am |
The above doesn’t work. The distribution is not known to be poisson. However for the above method to fail I think at least 1/3 of the numbers in the interval must be in clumps of 100k or more. This is a lot of clumping. Could it somehow interfere with what is known about the distribution of prime numbers. If so the above method could possibly be made to work.
Comment by Kristal Cantwell — October 3, 2009 @ 2:28 am |
I think I can fix the problem noted above. Here it is: If a quantum computer could produce a k digit random number x in polynomial(k) time then we could test x to see if it is prime. It has probability of 1/k of being prime. If we repeat this process 2k times the probability of not finding a prime is e^-2 which is less than 1/3. Since the testing time is a polynomial function of k the entire process should take place in polynomial time and that would put this problem in bqp and also make the problem polynomial if p = bqp.
Comment by Kristal Cantwell — October 3, 2009 @ 3:44 pm |
In regards to the above. I think everything except possibly the random number generator in the quantum computer will work. That is because there is a discussion on the wiki about finding primes with O(k) random bits:
http://michaelnielsen.org/polymath1/index.php?title=Finding_primes_with_O(k)_random_bits
So it looks if we have the random number generator we get what we want. There are also various random number generators available using various physical phenomena. The algorithm could be implemented with them but there is a problem that they may not be provably random.
Comment by Kristal Cantwell — October 4, 2009 @ 6:03 pm |
So from the above we need a random number generator for a quantum computer
to get this problem in BQP. I have a reference for one in the paragraph below
In the paper “Quantum theory, the Church-Turing principle and the universal quantum computer” by David Deutsch
in section 3, “Properties of the universal computer” after the first paragraph there is a subsection, “Random numbers and discrete stochastic systems” a program for a quantum computer generating true random numbers is given. The paper is available at:
Click to access quantum_theory.pdf
Comment by Kristal Cantwell — October 5, 2009 @ 3:16 pm |
I’ve tried to write up the overview of Ernie’s “polynomial strategy” (Thread 12) at
http://michaelnielsen.org/polymath1/index.php?title=Polynomial_strategy
But I was not able to understand Ernie’s point about how being able to quickly sum quadratic sums such as helps us sum the prime counting function
helps us sum the prime counting function  any faster… could this point be elaborated?
any faster… could this point be elaborated?
The squares, by the way, are the only numbers with an odd divisor function, so one can express as
as 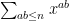 modulo 2. Not sure if this is helpful for anything…
modulo 2. Not sure if this is helpful for anything…
Comment by Terence Tao — September 19, 2009 @ 5:44 am |
It will take me a little time to write it up carefully, but let me just try to say right now what the idea is, in more detail: Basically, by first applying Odlyzko’s algorithm to restrict to an interval![[z,z+z^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bz%2Cz%2Bz%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) (or maybe the
(or maybe the  needs to be
needs to be  to get a gain), what it buys you is the fact that the contribution to the prime generating function for this interval of the divisors
to get a gain), what it buys you is the fact that the contribution to the prime generating function for this interval of the divisors  near to
near to  is small — that’s just because for any
is small — that’s just because for any  near
near  the geometric series
the geometric series
has only about terms. So, rather than working out the contributions of the generating functions for these large
terms. So, rather than working out the contributions of the generating functions for these large  one-by-one, one gets a savings by working with several at once.
one-by-one, one gets a savings by working with several at once.
Now let us suppose that , and let
, and let
A fragment of our generating function for the primes is the following sum
Now, as we said, each of these inner sums contain about terms. And, what we will do is rewrite it as a sum of about
terms. And, what we will do is rewrite it as a sum of about  sums, where each sum itself has about
sums, where each sum itself has about 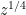 terms. *One* of these
terms. *One* of these  sums will be
sums will be
Note that the exponent here is quadratic in , though it certainly is *not* the toy sum
, though it certainly is *not* the toy sum 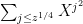 . And, the Strassen (or perhaps FFT's used in the right way) algorithm can evaluate it at
. And, the Strassen (or perhaps FFT's used in the right way) algorithm can evaluate it at  substantially faster than
substantially faster than 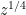 computations.
computations.
Now, this sum (2) has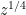 terms; and so, if it, and the other
terms; and so, if it, and the other  sums that make up (1), can be evaluated using fewer than
sums that make up (1), can be evaluated using fewer than 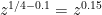 compuatations, then we have beaten in the “trivial'' (sum over the
compuatations, then we have beaten in the “trivial'' (sum over the 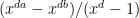 ) way to evaluate (1) above. Ok, this seems a little too much to ask for (even given our Strassen algorithm); but, replacing the
) way to evaluate (1) above. Ok, this seems a little too much to ask for (even given our Strassen algorithm); but, replacing the  by
by 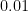 or
or  , it surely is true.
, it surely is true.
When one works with 's that are somewhat smaller than
's that are somewhat smaller than 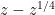 , one needs to work instead with
, one needs to work instead with  's that are in certain arithmetic progressions (instead of
's that are in certain arithmetic progressions (instead of  one would consider
one would consider 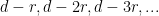 ); that is, for these smaller
); that is, for these smaller  , by working with arithmetic progressions one can get the
, by working with arithmetic progressions one can get the  's to dovetail, so that the same
's to dovetail, so that the same  isn't considered twice — I know that sounds too vague… I'll try to write it up in the next day or two.
isn't considered twice — I know that sounds too vague… I'll try to write it up in the next day or two.
Comment by Ernie Croot — September 20, 2009 @ 8:50 pm |
Ok after this, I’m going to just write everything up in latex and post on my website, instead of having to deal with “formula does not parse” again. Let me try to write up the missing “formula does not parse”:
where
and
[I fixed the bad LaTeX. Yes, the inability for commenters to edit their own comments is an annoying technical flaw in this format. It’s definitely a must-have for any future project of this type. -T.]
Comment by Ernie Croot — September 20, 2009 @ 8:54 pm |
I have started writing up the algorithm to evaluate the prime generating function quickly in![(F_2[x]/(g(x)))[X]](https://s0.wp.com/latex.php?latex=%28F_2%5Bx%5D%2F%28g%28x%29%29%29%5BX%5D&bg=ffffff&fg=000000&s=0&c=20201002) at
at  . But since it may take me a day or two to complete it, and since some people who want to think about it might not want to wait that long, I thought I would list out the link to what I have written so far (3 pages) — it will take shape over the next few days, and should become a polished draft by Wednesday (Sept 23):
. But since it may take me a day or two to complete it, and since some people who want to think about it might not want to wait that long, I thought I would list out the link to what I have written so far (3 pages) — it will take shape over the next few days, and should become a polished draft by Wednesday (Sept 23):
Click to access fast_primes.pdf
—-
Also, I thought I would explain why I didn’t post anything yesterday, as I said I would: I spent a great deal of time trying to work through two very promising approaches to solving Goal 1 in the note I wrote (and in the note on the polymath wiki). It looked like I had solved the problem completely, but alas these ideas fell apart on closer inspection. Perhaps in a few days I will post a link to a note describing several different approaches I have had, that turned out not to work, in the event somebody can see how to push them through.
Comment by Ernie Croot — September 21, 2009 @ 1:35 am |
Great! I’ll try to have a look at it soon.
It occurs to me that even if we don’t manage to formally prove Goal 1, we may be able to come up with a heuristic probabilistic argument or something (e.g. numerics) that would indicate that Goal 1 is true (with perhaps finitely many exceptions). If we then complete Goal 2 and Goal 3, we would then have a deterministic algorithm that works and reaches the square root barrier conditional on a concrete number-theoretic hypothesis, with a good chance of breaking that barrier. That’s already a reasonable result, though of course we would like to make the result unconditional if at all possible.
Comment by Terence Tao — September 21, 2009 @ 4:20 am |
The version of fast_primes.pdf up on my webpage right now basically has all the ideas in place. There may be some fussing about moving this or that constant around, and of course polishing it somewhat to make it more readable or getting the best-possible dependencies among various parameters, but all the key ideas are there. Unfortunately, I will not be able to complete the paper or polish it until much later in the week, as I have too many other things to do right now.
Comment by Ernie Croot — September 22, 2009 @ 3:02 pm |
OK, I read through the draft and I think I understand better what you are doing now… you are starting with the task of quickly summing multiple geometric series such as modulo some stuff, and use the geometric series formula to reduce matters to computing stuff like
modulo some stuff, and use the geometric series formula to reduce matters to computing stuff like 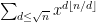 . Then you use Harald’s rational approximation ideas to chop this sum into a bunch of quadratic sums
. Then you use Harald’s rational approximation ideas to chop this sum into a bunch of quadratic sums  of non-negligible length, so that any improvement in one’s ability to sum quadratic sums leads to an improvement in the original summation.
of non-negligible length, so that any improvement in one’s ability to sum quadratic sums leads to an improvement in the original summation.
So this seems to establish Goals 2, 3 as long as t is small, but we still need to work out Goal 1, is that right?
Also, the original Odlyzko step to reduce to an interval of size n^{0.51} seems to not yet be used, though I can imagine it would be useful for Goal 1 by improving the sparsity of various key polynomials… would you agree?
Comment by Terence Tao — September 23, 2009 @ 7:39 am |
Exactly right (I guess it really is some polynomial analogue of Harald’s idea, though there are some extra subtleties), including the last point about using Odlyzko’s idea (one can still quickly compute the prime generating function, its just that it may have no terms at all). Curiously, if one doesn’t restrict to the interval of width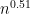 at the outset, then one cannot use this polynomial analogue of Harald’s idea (at least I don’t see how to do it so as to run faster than
at the outset, then one cannot use this polynomial analogue of Harald’s idea (at least I don’t see how to do it so as to run faster than  ) that I used to obtain a speedup.
) that I used to obtain a speedup.
And yes, Goal 1 is the main task to complete right now. One idea for this is to find a way to compute the prime generating function for the interval![[z,z+z^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bz%2Cz%2Bz%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , with the primes restricted to certain arithmetic progressions
, with the primes restricted to certain arithmetic progressions 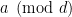 , where
, where  is fixed and
is fixed and  varies. The point would be that (a) there are a lot fewer primes in each of these progressions than in the whole interval (there should be about
varies. The point would be that (a) there are a lot fewer primes in each of these progressions than in the whole interval (there should be about  of them), meaning that one doesn’t have to evaluate the prime generating function at
of them), meaning that one doesn’t have to evaluate the prime generating function at  , but instead only
, but instead only  (even just using the Vandermonde idea will show this); and (b) of course you don’t know in advance which of the progressions
(even just using the Vandermonde idea will show this); and (b) of course you don’t know in advance which of the progressions 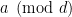 contains primes, but there might be a way to relate the generating function for one progression
contains primes, but there might be a way to relate the generating function for one progression 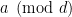 to all the others
to all the others  (or at least to some of the
(or at least to some of the 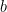 ‘s), thereby greatly speeding things up — I don’t have time to explain why I think this might be possible right now, but maybe I will write this up this weekend instead of finishing the writeup on the fast evaluation of the prime generating function, since I think anyone can see now how it works.
‘s), thereby greatly speeding things up — I don’t have time to explain why I think this might be possible right now, but maybe I will write this up this weekend instead of finishing the writeup on the fast evaluation of the prime generating function, since I think anyone can see now how it works.
Another idea for how to attack Goal 1 is to attempt to rewrite the matrix with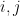 th entry equal to the geometric series
th entry equal to the geometric series  , that we wish to show doesn’t have the vector
, that we wish to show doesn’t have the vector  in its kernel. I spent some time trying to look at variants of this matrix that still would be useful to our problem (such as permuting entries on each row, which doesn’t affect the problem of whether
in its kernel. I spent some time trying to look at variants of this matrix that still would be useful to our problem (such as permuting entries on each row, which doesn’t affect the problem of whether 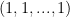 is in its kernel), and I was inspired by some identities such as the fact that the 2 variable Wronskian factors nicely into a product of two 1 variable Wronskians (as is used to show non-vanishing of certain partial derivatives in the usual proof of the Thue-Siegel-Dyson theorem). I spent a fair amount of time trying various other types of related identities, but couldn’t quite get what I needed. I suppose this idea is related to the way that I applied Strassen to represent polynomial evaluation at multiple points by a matrix product problem (involving Vandermondes or quasi-Vandermondes).
is in its kernel), and I was inspired by some identities such as the fact that the 2 variable Wronskian factors nicely into a product of two 1 variable Wronskians (as is used to show non-vanishing of certain partial derivatives in the usual proof of the Thue-Siegel-Dyson theorem). I spent a fair amount of time trying various other types of related identities, but couldn’t quite get what I needed. I suppose this idea is related to the way that I applied Strassen to represent polynomial evaluation at multiple points by a matrix product problem (involving Vandermondes or quasi-Vandermondes).
Another way to try to show that the matrix doesn’t have in its kernel, or has no kernel at all, is to think in terms of interpolation. For example, one way to show that Vandermondes don’t vanish — in a way quite different from the approach of just computing their determinant — is to show that one can construct a polynomial of a given degree
in its kernel, or has no kernel at all, is to think in terms of interpolation. For example, one way to show that Vandermondes don’t vanish — in a way quite different from the approach of just computing their determinant — is to show that one can construct a polynomial of a given degree  that takes on any values at all, at any given set of
that takes on any values at all, at any given set of  points, which can be done using, say, the Lagrange interpolation formula. Might there be some equivalent of the interpolation idea for our matrix of geometric series?
points, which can be done using, say, the Lagrange interpolation formula. Might there be some equivalent of the interpolation idea for our matrix of geometric series?
Another idea is to use the fact that we have control of the polynomial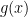 — we can take it to be whatever we want, and so why not take it to be something that makes the task of evaluating the generating function at lot easier. I played around with this some. One that I tried was
— we can take it to be whatever we want, and so why not take it to be something that makes the task of evaluating the generating function at lot easier. I played around with this some. One that I tried was  . My reasoning for thinking about this one was that when you mod a high power of
. My reasoning for thinking about this one was that when you mod a high power of  out by it, you get a product of a power of
out by it, you get a product of a power of  and a power of
and a power of  ; and then, you can use the binomial theorem to think about the coefficients of that power of
; and then, you can use the binomial theorem to think about the coefficients of that power of  (as in the formula
(as in the formula  ).
).
I will write up several more ideas I have had this weekend (including a way to look for collisions between two generating functions for subsets of primes in![[z,z+z^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bz%2Cz%2Bz%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) ) …
) …
Comment by Ernie Croot — September 23, 2009 @ 3:45 pm |
OK, thanks for the clarifications about the role of Odlyzko’s method
I quite like the first approach to Goal 1. It now seems that for any a, b in![[x, x+x^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2Bx%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , the polynomial
, the polynomial 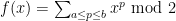 has an arithmetic circuit complexity of
has an arithmetic circuit complexity of 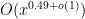 , so in particular for any g(x) of degree at most
, so in particular for any g(x) of degree at most  (say),
(say), 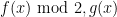 can be computed in time
can be computed in time  (say). Setting g(x) to be the polynomial
(say). Setting g(x) to be the polynomial  , this allows us to compute the parity of the number of primes in [a,b] equal to a given residue class modulo q. We can do this for all
, this allows us to compute the parity of the number of primes in [a,b] equal to a given residue class modulo q. We can do this for all  and still stay under the square root barrier in cost.
and still stay under the square root barrier in cost.
Probabilistically, it seems extremely unlikely that one could ever find an interval [a,b] in![[x,x+x^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bx%2Cx%2Bx%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) with a non-zero number of primes, such that the set of such primes intersects every residue class mod q for
with a non-zero number of primes, such that the set of such primes intersects every residue class mod q for  in an even number of elements, but I don’t see currently how to rule out this possibility.
in an even number of elements, but I don’t see currently how to rule out this possibility.
What made the AKS argument work, by the way, was a multiplicativity property that greatly amplified the various algebraic identities they had; more precisely, if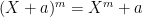 and
and  , where X is a root of unity of order coprime to n,m, then also
, where X is a root of unity of order coprime to n,m, then also 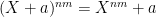 . This allowed them to exponentiate a polylogarithmic number of algebraic identities into a superpolynomial number. We don’t seem to have discovered an analogous amplification trick here yet, but perhaps we will eventually.
. This allowed them to exponentiate a polylogarithmic number of algebraic identities into a superpolynomial number. We don’t seem to have discovered an analogous amplification trick here yet, but perhaps we will eventually.
Comment by Terence Tao — September 23, 2009 @ 10:52 pm |
Here I will talk about the first idea from my last posting. Recall that the idea was to take the interval![I := [z, z + z^{0.51}]](https://s0.wp.com/latex.php?latex=I+%3A%3D+%5Bz%2C+z+%2B+z%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , and consider the generating function for the primes in it that are
, and consider the generating function for the primes in it that are 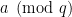 , for some
, for some  . In what follows I will be thinking
. In what follows I will be thinking 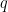 as a small power of
as a small power of  , though hopefully in later version of the arguments it can be taken closer to
, though hopefully in later version of the arguments it can be taken closer to  .
.
Essentially, I hope to show (a) how the work one does on computing the prime generating function for primes that are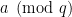 can be used to speed up the process for other progressions
can be used to speed up the process for other progressions  ; and, (b) find a way to skip past certain progressions
; and, (b) find a way to skip past certain progressions 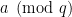 whose generating function
whose generating function  vanishes at
vanishes at  mod
mod 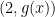 . Completing this second task would be especially important for producing an algorithm to locate primes that breaks the square-root barrier.
. Completing this second task would be especially important for producing an algorithm to locate primes that breaks the square-root barrier.
Let us first note that without attempting these tasks, working with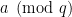 already gives us a speedup over the “trivial algorithm” used to evaluate the prime generating function at
already gives us a speedup over the “trivial algorithm” used to evaluate the prime generating function at  , where
, where 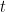 is the number of primes under consideration (
is the number of primes under consideration (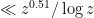 in the case where we work with all the primes in $I$). The speedup comes from two directions: first, when one goes to compute the generating function, only at most about
in the case where we work with all the primes in $I$). The speedup comes from two directions: first, when one goes to compute the generating function, only at most about  or so of the divisors
or so of the divisors  contribute a term
contribute a term  . Basically, what happens is that quite often none of the products
. Basically, what happens is that quite often none of the products
are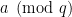 , at least it is the case when
, at least it is the case when  is sufficiently near to
is sufficiently near to  . And the second place where we get a speedup is the fact that if we work with the primes that are
. And the second place where we get a speedup is the fact that if we work with the primes that are 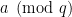 , we only need evaluate the generating function at
, we only need evaluate the generating function at  , and check for non-vanishing mod
, and check for non-vanishing mod 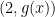 . The reason is that even just using the “Vandermonde method”, since the generating function has at most about
. The reason is that even just using the “Vandermonde method”, since the generating function has at most about  terms, one only needs to check non-vanishing for that many powers of
terms, one only needs to check non-vanishing for that many powers of  .
.
I had thought that I could solve task (b) this past weekend, but it didn’t seem to work out. Basically, what I tried to do was to show that there exists a polynomial , of not too large degree (say of degree
, of not too large degree (say of degree  in each variable), such that for certain small values of
in each variable), such that for certain small values of 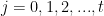 , when one evaluates
, when one evaluates  , one gets the prime generating function for the primes in our interval that lie in a certain arithmetic progression
, one gets the prime generating function for the primes in our interval that lie in a certain arithmetic progression  . The hope then was to show that by solving for
. The hope then was to show that by solving for  making
making  , one could “skip ahead” to a progression
, one could “skip ahead” to a progression  containing loads of primes. I still think this method has a decent chance of succeeding, and I will try to take another pass at proving it in a few days, when I am less busy.
containing loads of primes. I still think this method has a decent chance of succeeding, and I will try to take another pass at proving it in a few days, when I am less busy.
—-
On another front, I discovered that one can factor the matrix of geometric series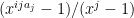 that comes up in our problem — it can be written as a product
that comes up in our problem — it can be written as a product 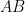 , where the matrix
, where the matrix  is
is  (or thereabouts), and where
(or thereabouts), and where  is
is  .
.  is basically a Vandermonde, whose
is basically a Vandermonde, whose  th row is
th row is
where the integers in our interval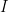 are
are 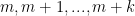 .
.  , on the other hand, is a 0-1 matrix, with a
, on the other hand, is a 0-1 matrix, with a  in the
in the  th row and
th row and  th column when
th column when  divides the
divides the  th number of our interval. Although this matrix factorization is not as non-trivial as one would like, it might at least allow one to more easily see such things as the fact that our matrix
th number of our interval. Although this matrix factorization is not as non-trivial as one would like, it might at least allow one to more easily see such things as the fact that our matrix 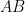 of geometric series has large rank (assuming it does — surely it does).
of geometric series has large rank (assuming it does — surely it does).
I can certainly imagine how to show that has large rank, and of course we know that
has large rank, and of course we know that  has large rank from the fact that it is a fragment of a Vandermonde. If we could somehow relate the kernel of
has large rank from the fact that it is a fragment of a Vandermonde. If we could somehow relate the kernel of  to the image of
to the image of  , we would be done as far as showing that
, we would be done as far as showing that 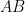 has large rank.
has large rank.
I feel that other kinds of matrix factorization can be found, some more useful than the one above. The reason I say this is that the Chinese Remainder Theorem can be encoded as a matrix product: say you have two 0-1 vectors of length . For the first one, put a
. For the first one, put a  in the
in the  th position if
th position if 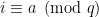 , and 0 otherwise; and, do the same for the second vector, but put
, and 0 otherwise; and, do the same for the second vector, but put  in the
in the  th position if
th position if 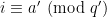 . Taking the dot product of these two vectors gives you the number of integers up to
. Taking the dot product of these two vectors gives you the number of integers up to  that are in both of these progressions at once. One can imagine several ways of using this fact (actually, generalizations of it, where the
that are in both of these progressions at once. One can imagine several ways of using this fact (actually, generalizations of it, where the  ‘s are replaced by powers of
‘s are replaced by powers of  ) to produce factorizations of matrices like our
) to produce factorizations of matrices like our 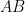 …
…
Comment by Ernie Croot — September 28, 2009 @ 3:24 pm |
One more thing: the polynomial I tried to construct above, although of large degree (say at most
I tried to construct above, although of large degree (say at most  in each variable), was to be very sparse, say having fewer than
in each variable), was to be very sparse, say having fewer than 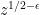 terms. Without the sparseness, it would be useless as far as allowing one to “skip ahead”.
terms. Without the sparseness, it would be useless as far as allowing one to “skip ahead”.
Comment by Ernie Croot — September 28, 2009 @ 3:30 pm |
It occurred to me that one can write the geometric series in a different way than a sum of a few polynomials
in a different way than a sum of a few polynomials  that is nicer from the point of view of an eventual application of FFTs or related methods. First, let me discuss the problem with using the geometric series formula, and expressions such as
that is nicer from the point of view of an eventual application of FFTs or related methods. First, let me discuss the problem with using the geometric series formula, and expressions such as  : First, the
: First, the  in the denominator of the geometric series formula is quite nasty to deal with, both for FFTs and probably also methods to show that certain matrices (that I have discussed in previous postings) are nonsingular. And the trouble with the
in the denominator of the geometric series formula is quite nasty to deal with, both for FFTs and probably also methods to show that certain matrices (that I have discussed in previous postings) are nonsingular. And the trouble with the  is that it is the composition of two not-so-trivial polynomials, namely the
is that it is the composition of two not-so-trivial polynomials, namely the  th power map, for
th power map, for  not too small, and the translated power map
not too small, and the translated power map  — compositions of this sort seem quite hard for FFTs to handle, though it doesn’t seem as bad as the geometric series formulas (at least not to me). If in place of the power
— compositions of this sort seem quite hard for FFTs to handle, though it doesn’t seem as bad as the geometric series formulas (at least not to me). If in place of the power  , we had something quite a bit smaller — bounded, in fact — while perhaps increasing the number of terms in our lacunary
, we had something quite a bit smaller — bounded, in fact — while perhaps increasing the number of terms in our lacunary 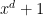 a little bit (but not by too much), it would seem to me to be much easier for an FFT approach to get somewhere, for a variety of reasons I don’t want to get into. Well, there *are* identities that we can use in place of these that are better in this sense; specifically, consider the “base
a little bit (but not by too much), it would seem to me to be much easier for an FFT approach to get somewhere, for a variety of reasons I don’t want to get into. Well, there *are* identities that we can use in place of these that are better in this sense; specifically, consider the “base  generating function” identity
generating function” identity
If, say, we use and perhaps
and perhaps  , then if our geometric progression is to go up to about
, then if our geometric progression is to go up to about  , we basically can use
, we basically can use 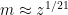 — that is, we have the product of
— that is, we have the product of 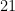 polynomials with few terms.
polynomials with few terms.
Identities of this sort might also be easier to deal with when showing that our various geometric series matrices are nonsingular, the reason being that in the matrices that come up, each entry will be the product of only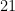 lacunary polynomials. It is not difficult (at least I don’t think so) to relate the non-singularity of matrices with lacunary polynomial entries, evaluated down at column at
lacunary polynomials. It is not difficult (at least I don’t think so) to relate the non-singularity of matrices with lacunary polynomial entries, evaluated down at column at 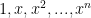 , with the non-singularity of certain Vandermonde matrices; and if the same can be said for matrices where each entry is a small number of products of lacunary polynomials, then we are in business!
, with the non-singularity of certain Vandermonde matrices; and if the same can be said for matrices where each entry is a small number of products of lacunary polynomials, then we are in business!
Comment by Ernie Croot — September 30, 2009 @ 4:28 am |
Let me add to this, in case I wasn’t clear: We know how to compute the prime generating function at altogether in time below the square-root barrier. But it would be nice to be able to take this all the way up to about
altogether in time below the square-root barrier. But it would be nice to be able to take this all the way up to about  or so. If the generating function were just a polynomial having about
or so. If the generating function were just a polynomial having about  terms, then perhaps an FFT method would do it; but we don’t have that, so we have to hunt around for identities to put the generating function in a form that is “good enough” for some generalization of the standard FFT methods to work.
terms, then perhaps an FFT method would do it; but we don’t have that, so we have to hunt around for identities to put the generating function in a form that is “good enough” for some generalization of the standard FFT methods to work.
Comment by Ernie Croot — September 30, 2009 @ 8:09 pm |
Ernie –
I’ve been away from this page for a short while, and I suspect I am not the only one who is having difficulty following – you seem to be doing all of the work right now. Would you mind typing up a sketch of your overall strategy, including why you think working with polynomials is best?
Comment by H A Helfgott — October 1, 2009 @ 4:01 pm |
Here is a link to an article about the polynomial strategy:
http://michaelnielsen.org/polymath1/index.php?title=Polynomial_strategy
Comment by Kristal Cantwell — October 1, 2009 @ 5:36 pm |
Harald — I have been preoccupied lately writing up my NSF grant proposal, which is due in 2 days, so I don’t have time right now to do much. As Kristal pointed out below, I think Terry has put up some of it on the webpage, but there is still lots more to put up there.
Right now, the main problem is to confront Goal 1 in my previous postings. One idea is to try to maneuver around it altogether by restricting to arithmetic progressions in![[z, z + z^{0.51}]](https://s0.wp.com/latex.php?latex=%5Bz%2C+z+%2B+z%5E%7B0.51%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , but I am feeling less optimistic about that approach just now. Last night, before going to sleep, it occurred to me that one can change Goal 1 into a different sort of problem related to inner products — instead of trying to show that a certain Vandermonde-like matrix is non-singular, one can attempt to show that in a certain sequence of square matrices, one induces an inner product in which
, but I am feeling less optimistic about that approach just now. Last night, before going to sleep, it occurred to me that one can change Goal 1 into a different sort of problem related to inner products — instead of trying to show that a certain Vandermonde-like matrix is non-singular, one can attempt to show that in a certain sequence of square matrices, one induces an inner product in which  is not self-orthogonal. I know that’s nowhere near a good enough description — when this grant business is all over with, I will be able to devote a lot more time to writing things up properly…
is not self-orthogonal. I know that’s nowhere near a good enough description — when this grant business is all over with, I will be able to devote a lot more time to writing things up properly…
Comment by Ernie Croot — October 1, 2009 @ 8:07 pm |
Yeah, I should be doing more of this, but I have been preoccupied with my Australia trip recently. But thanks for reminding me about it. Some of this is indeed on the wiki, but I can try to condense it here:
Basically, Ernie has a reasonably quick way of computing the expression for intervals
for intervals ![[a,b] \subset [1,N]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D+%5Csubset+%5B1%2CN%5D&bg=ffffff&fg=000000&s=0&c=20201002) of length at most
of length at most  and polynomials g of low degree (degree
and polynomials g of low degree (degree  . This expression can be computed in something like
. This expression can be computed in something like 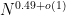 time. This recovers the earlier result that the parity of the number of primes in [a,b] can be computed in this time, but we can now also do things like the parity of the number of primes in [a,b] that is equal to r mod q for any
time. This recovers the earlier result that the parity of the number of primes in [a,b] can be computed in this time, but we can now also do things like the parity of the number of primes in [a,b] that is equal to r mod q for any 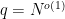 .
.
(The way this is computed, by the way, is basically to rewrite mod 2 as
mod 2 as  , and use Farey sequences to represent the domain of summation of (d,m) as a polygon. After one application of the geometric series formula, it reduces to the task of evaluating quadratic sums such as
, and use Farey sequences to represent the domain of summation of (d,m) as a polygon. After one application of the geometric series formula, it reduces to the task of evaluating quadratic sums such as  in o(J) time.)
in o(J) time.)
Ideally, we would like to have a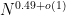 algorithm for determining whether an interval [a,b] of length
algorithm for determining whether an interval [a,b] of length  is completely devoid of primes, as this would then (with a binary search) locate a prime in about the same amount of time. [Using Odlyzko's Riemann zeta method one can locate an interval of length
is completely devoid of primes, as this would then (with a binary search) locate a prime in about the same amount of time. [Using Odlyzko's Riemann zeta method one can locate an interval of length 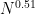 with at least one prime in time
with at least one prime in time 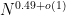 .] The problem is that currently, to do this, we need to test
.] The problem is that currently, to do this, we need to test  for far too many choices of g – about
for far too many choices of g – about 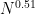 , in fact, leading to a total run time closer to N than to
, in fact, leading to a total run time closer to N than to 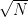 . The hope is to use an FFT method (or, failing that, something weaker such as Strassen fast multiplication) to cut down on the computational cost, or to use some number theoretic or Vandermonde determinant magic to cut down on the number of g one needs to test. (Note that the latter route is basically the secret to the AKS algorithm.)
. The hope is to use an FFT method (or, failing that, something weaker such as Strassen fast multiplication) to cut down on the computational cost, or to use some number theoretic or Vandermonde determinant magic to cut down on the number of g one needs to test. (Note that the latter route is basically the secret to the AKS algorithm.)
Comment by Terence Tao — October 1, 2009 @ 11:36 pm |
This is slightly tangential to the main program, but it occurred to me just now that there was an analogy here between what we are doing and polynomial identity testing. In particular, if we can find a way to compute in polynomial time for g of logarithmic size, then the problem of determining whether [a,b] contains a prime should be a BPP problem (if it does, then the above expression will be non-zero for a non-trivial fraction of the g’s, I think, by the large sieve or something). So this would solve the original finding primes problem subject to P=BPP (which we were not able to do before because of a pseudoprime counterexample).
in polynomial time for g of logarithmic size, then the problem of determining whether [a,b] contains a prime should be a BPP problem (if it does, then the above expression will be non-zero for a non-trivial fraction of the g’s, I think, by the large sieve or something). So this would solve the original finding primes problem subject to P=BPP (which we were not able to do before because of a pseudoprime counterexample).
Comment by Terence Tao — October 2, 2009 @ 12:57 am |
I recently came across the following paper that looks like it might be highly relevant to our problem of quickly evaluating the prime generating function at many points:
Click to access U07.pdf
I am particularly interested in the multi-point, multi-variable polynomial composition evaluation algorithm, and I think there is a chance that it can be used to evaluate our generating function at many points as quickly as we could hope for.
On another matter, I spent the past two weeks trying about a dozen different ideas for attacking Goal 1 (including the one I mentioned above in response to Harald’s question), though most didn’t work out. What I am trying to do right now is prove not only Goal 1, but in fact a strengthening of it, where we only need evaluate the generating function at , in order to find a point where it doesn’t vanish. My idea is to try to rewrite our generating function
, in order to find a point where it doesn’t vanish. My idea is to try to rewrite our generating function 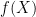 in the form
in the form
where the and
and 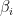 are sparse polynomials such that the total number of terms among all of them is at most, say,
are sparse polynomials such that the total number of terms among all of them is at most, say,  . If this can be accomplished, then our strengthening of Goal 1 would following from the following conjecture:
. If this can be accomplished, then our strengthening of Goal 1 would following from the following conjecture:
Click to access good_rank2.pdf
The contribution of the geometric series
for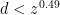 , say, can be put into this form (*) using the ideas from comment 19 above. What I attempted to do for those
, say, can be put into this form (*) using the ideas from comment 19 above. What I attempted to do for those  satisfying
satisfying
was to unwind our Strassen algorithm approach to evaluating sums like , and I *was* able to put express this as a sum of a small number of
, and I *was* able to put express this as a sum of a small number of  , but unfortunately the total number of terms among these
, but unfortunately the total number of terms among these  and
and 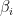 together, was too big.
together, was too big.
The next approach I tried was to make use of the fact that the particular Strassen matrices we use have a certain self-similarity — turns out that each of the two matrices that arise can be broken up into blocks, where each block can be expressed in terms of the others. The hope, then, is to develop an alternative to Strassen's method, using the special properties of these matrices (which is not shared by matrices that would come up in more general multi-point evaluation problems). So far I have not succeeded…
Another idea for how to put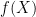 into the form (*) is to unwind the algorithms in the above paper I linked to (containing the multi-point algorithm), just like I unwound the Strassen approach. I don't think will work, however, because the multi-point algorithms make special use of the polynomial
into the form (*) is to unwind the algorithms in the above paper I linked to (containing the multi-point algorithm), just like I unwound the Strassen approach. I don't think will work, however, because the multi-point algorithms make special use of the polynomial 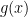 to achieve its speedup — I think, for various reasons, we need a method that is independent of the
to achieve its speedup — I think, for various reasons, we need a method that is independent of the 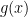 .
.
On another front, I have some ideas for how to prove the Conjecture liked to above (the like to my homepage). In particular, there are slight generalizations of Vanermonde determinant formulas that look like they might be relevant, for various reasons. Specifically, let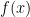 be a polynomial with
be a polynomial with  terms, let
terms, let  be any distinct integers, and let
be any distinct integers, and let  be the matrix whose
be the matrix whose 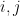 entry is
entry is  . Then, the determinant of
. Then, the determinant of  is something like
is something like
And now, one can think of the rows of this matrix as corresponding to a product
as corresponding to a product 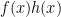 , where
, where  — basically, writing this polynomial as
— basically, writing this polynomial as 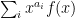 , each term corresponds to a column of the matrix. Ok, so that's just one polynomial — maybe the matrix corresponding to a sum of products like this can likewise be analyzed.
, each term corresponds to a column of the matrix. Ok, so that's just one polynomial — maybe the matrix corresponding to a sum of products like this can likewise be analyzed.
Comment by Ernie Croot — October 21, 2009 @ 10:07 pm |
Looking closer at the paper I linked to in the previous post, I am not as enthusiastic now that it will help us to evaluate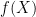 quickly at lots of points. But it gave me an idea that I think might lead somewhere: Suppose that
quickly at lots of points. But it gave me an idea that I think might lead somewhere: Suppose that 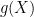 has degree
has degree  , where
, where  , say. Then, the order of
, say. Then, the order of  mod
mod 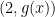 is about
is about  . What this means is that if
. What this means is that if  is a polynomial
is a polynomial
then if we let
then we have that for all integers ,
,
So, if is our prime generating function, then if we can find the corresponding polynomial
is our prime generating function, then if we can find the corresponding polynomial  quickly enough (and we can try to do this in
quickly enough (and we can try to do this in ![C[x]](https://s0.wp.com/latex.php?latex=C%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) , say, where things might be easier), which has degree at most
, say, where things might be easier), which has degree at most  , we can use an
, we can use an 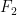 FFT to evaluate it at
FFT to evaluate it at 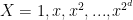 in time
in time 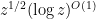 . And, since the field
. And, since the field ![F_2[x]/(g(x))](https://s0.wp.com/latex.php?latex=F_2%5Bx%5D%2F%28g%28x%29%29&bg=ffffff&fg=000000&s=0&c=20201002) (we assume
(we assume  was irreducible) contains $2^d$ roots of unity we don’t have to even be clever about how exactly to use FFTs for our fast evaluation problem, as these powers of
was irreducible) contains $2^d$ roots of unity we don’t have to even be clever about how exactly to use FFTs for our fast evaluation problem, as these powers of  *are* our
*are* our  th roots of unity.
th roots of unity.
There is one point to worry about here, concerning how this would fit in with Goal 1: In crafting Goal 1 we had assumed that had quite large order, say order
had quite large order, say order 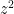 or something (see the original note where I introduced Goal 1), yet for the above idea to work we need to work with much smaller values for the order of
or something (see the original note where I introduced Goal 1), yet for the above idea to work we need to work with much smaller values for the order of  . Well, it’s probably ok to do this — I haven’t thought through yet the consequences of using a
. Well, it’s probably ok to do this — I haven’t thought through yet the consequences of using a 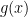 of such low degree. If a stronger version of Goal 1 could be proved, where one only needs to evaluate
of such low degree. If a stronger version of Goal 1 could be proved, where one only needs to evaluate 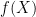 at
at  or so, then maybe we can even take
or so, then maybe we can even take 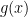 of degree $d$ satisfying
of degree $d$ satisfying  or so.
or so.
Comment by Ernie Croot — October 22, 2009 @ 5:33 am |
Hmm, this is interesting; it is the first time I have seen this approach give (or have the potential to give) a run time close to , rather than
, rather than  which seemed to be what the previous approaches were giving (each individual evaluation of
which seemed to be what the previous approaches were giving (each individual evaluation of 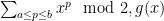 could be evaluated below the square root barrier, but the number of such evaluations was also close to the square root).
could be evaluated below the square root barrier, but the number of such evaluations was also close to the square root).
I’m still a bit worried though that when scanning an interval [a,b] of length for primes, one may need to evaluate the polynomial at about
for primes, one may need to evaluate the polynomial at about  points, because otherwise I don’t see how to prevent the polynomial
points, because otherwise I don’t see how to prevent the polynomial  from factorising as the product of the minimal polynomials of all the points being tested. (Here I am assuming that the minimal polynomials have degree
from factorising as the product of the minimal polynomials of all the points being tested. (Here I am assuming that the minimal polynomials have degree  .) This would keep the run time above
.) This would keep the run time above  unless there was some way to test for non-vanishing at these points with sublinear efficiency.
unless there was some way to test for non-vanishing at these points with sublinear efficiency.
It would of course be highly unlikely that this polynomial would be so smooth, but one would need some algebraic miracle or something to rigorously show that this doesn’t happen…
Comment by Terence Tao — October 22, 2009 @ 6:13 am |
One observation following your comment: suppose in the interval [a,b] there were exactly two primes, and they differed by a multiple of for some m. Then
for some m. Then  would vanish for any g of degree at most m. So it does seem that we need g of moderately large degree (larger than
would vanish for any g of degree at most m. So it does seem that we need g of moderately large degree (larger than  ) in order to deterministically detect primes.
) in order to deterministically detect primes.
Comment by Terence Tao — October 22, 2009 @ 6:38 am |
It occurred to me that we might be able to show that the task of determining whether a prime lies in [a,b] could lie in BPP, at least. (This is not a triviality; on the wiki page http://michaelnielsen.org/polymath1/index.php?title=Oracle_counterexample_to_finding_pseudoprimes , there is a reasonable case that one could concoct a set of pseudoprimes for which one could not solve this problem quickly even when P=BPP.) The point is that testing polynomial identities over finite fields is in BPP, because such an identity either holds everywhere or fails for a large fraction of inputs, and so can be placed in BPP by random sampling. And this whole approach is basically polynomial identity testing.
Actually, now that I think about it, we won’t get BPP, but rather BP- , which isn’t nearly as impressive, but still non-trivial at least…
, which isn’t nearly as impressive, but still non-trivial at least…
Comment by Terence Tao — October 22, 2009 @ 6:22 am |
If the a quantum computer has a random number generator and can simulate a turing machine couldn’t it solve BQP problems?
In fact from
http://en.wikipedia.org/wiki/BQP
BQP contains BPP
Furthermore since we have a source of randomness in BPP and the density is 1/log b for primes then using the random source to get a random candidate will give a number that has 1/log b probability of being prime repeating this 2log b times will give success with probability 1-(1-1/log b)^(2log b) or roughly 1-(e^-2) which means probability of failure is less than 1/3. I may be missing seeing something but it looks like the problem is in both BQP and BPP.
Comment by Kristal Cantwell — October 22, 2009 @ 4:56 pm |
Kristal, complexity classes such as P, BPP, NP, BQP, etc. apply only to decision problems (“Yes/No” questions), not search problems (“Find an X”). Finding a prime is a search problem, not a decision problem, and so does not lie in P, BPP, etc.
A relevant decision problem, though, is “Does there exist a prime in the interval [a,b]?”. If one can solve this decision problem quickly, one can solve the search problem quickly, by a binary search starting from [x,2x].
It is still open whether this decision problem is in BPP. The problem is that the density of primes in [a,b] could be very low, and so it is not clear even after polylogarithmically many searches that one has a 2/3 chance or more of finding a prime (the needle in the haystack problem). But it seems from Ernie’s work that this problem is at least in BP- when
when  , by which I mean that there is a probabilistic algorithm which after
, by which I mean that there is a probabilistic algorithm which after  work will correctly determine whether there is a prime or not in [a,b] with a failure probability of at most 1/3 in either case.
work will correctly determine whether there is a prime or not in [a,b] with a failure probability of at most 1/3 in either case.
Comment by Terence Tao — October 22, 2009 @ 5:40 pm |
You are right BPQ is for decisions. There is FBPQ see
http://qwiki.stanford.edu/wiki/Complexity_Zoo:F
I think there should also be a FBPP but I can’t find it.
I think the problem is is FBPQ. We are given 10^k to 10^k+1
with a quantum number computer we have random numbers and can guess randomly each guess and test is polynomial in k
and and has probability of success 1/k so if we repeat this test 2k times we should have probabliity of success 1-e^2
and we should have the problem in FBQP. This looks better than any search involving z^.49 because I think z is exponential in k. If FBPP were defined as FBPQ then something similar should show the problem is in FBPP.
Comment by Kristal Cantwell — October 26, 2009 @ 7:14 pm |
That should be BQP and FBQP in the above instead of BPQ and FBPQ. Also the problem is in BQP rather than is is BQP. Sorry about these errors.
Comment by Kristal Cantwell — October 26, 2009 @ 7:28 pm |
I finally got around to looking up the fast multiplication algorithms in Knuth’s book “Semi-numerical Algorithms” that I had talked about before, and it turns out that one of these is called “Karatsuba’s identity”, which is somewhat similar to Strassen’s identity, only it doesn’t involve matrices is a lot easier to use. In fact, I think there is a chance of using it in combination with FFTs to get a quick-running algorithm to evaluate our prime generating function. Here is the idea: Suppose that we can write
where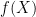 is our generating function for the primes in
is our generating function for the primes in ![[z,z+z^{0.501}]](https://s0.wp.com/latex.php?latex=%5Bz%2Cz%2Bz%5E%7B0.501%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , and where the
, and where the  and
and 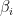 are polynomials such that the total number of terms among all of them is at most, say,
are polynomials such that the total number of terms among all of them is at most, say,  or so. What we would like to do is quickly evaluate
or so. What we would like to do is quickly evaluate 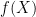 at, say,
at, say,
where or so; and, we’d like to be able to do this using a lot fewer than
or so; and, we’d like to be able to do this using a lot fewer than  operations.
operations.
Now let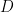 be some integer (that we choose later), and write each of the
be some integer (that we choose later), and write each of the  as
as
where
and
where are the coefficients of
are the coefficients of  ; and, write
; and, write  similarly — that is,
similarly — that is,
Ideally, we want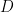 to be such that each
to be such that each  have about half as many terms as
have about half as many terms as  , and we want the analogous to hold for the
, and we want the analogous to hold for the  — of course, in order to guarantee that this is possible, we would have to be able to select that decomposition for
— of course, in order to guarantee that this is possible, we would have to be able to select that decomposition for 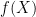 above carefully.
above carefully.
Now, assuming that we can find such a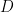 (and have such a decomposition for
(and have such a decomposition for 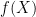 ), we then observe the following, which is basically Karatsuba’s identity:
), we then observe the following, which is basically Karatsuba’s identity:
where
The point here is that we have replaced on sum of products of two polynomials (the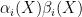 ) with three sums of such products, but where each polynomial has degree about half what we had before — each of these sums (forgetting the factors
) with three sums of such products, but where each polynomial has degree about half what we had before — each of these sums (forgetting the factors 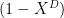 and so on) involves products of two polynomials of degree at most
and so on) involves products of two polynomials of degree at most 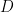 . The idea is then to iterate the above process, starting with *these* sums, and then replacing each by three sums of products of polynomials each of degree
. The idea is then to iterate the above process, starting with *these* sums, and then replacing each by three sums of products of polynomials each of degree 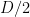 , and so on. Eventually, we get down to sums of products of polynomials that we can just expand out by trivial methods, as they will have few terms to begin with, and then apply FFTs to evaluate them at the points (*) above.
, and so on. Eventually, we get down to sums of products of polynomials that we can just expand out by trivial methods, as they will have few terms to begin with, and then apply FFTs to evaluate them at the points (*) above.
Unfortunately, it is not always the case that the new polynomials produced at each iteration have fewer terms, since the and
and 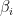 may have been sparse to begin with (in fact, likely are). But what we can hope for is that the initial polynomials
may have been sparse to begin with (in fact, likely are). But what we can hope for is that the initial polynomials  and
and 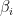 can be chosen carefully so that after a small number of iterations, we get “mixing” — that is, the number of terms in, say, each of the polynomials
can be chosen carefully so that after a small number of iterations, we get “mixing” — that is, the number of terms in, say, each of the polynomials
is not much bigger than the number in each of
In other words, we will want that sufficiently many iterations into the above process we have that, say, shares many terms in common with
shares many terms in common with  , and the same for the
, and the same for the  ‘s.
‘s.
Comment by Ernie Croot — October 25, 2009 @ 3:31 am |
[…] Terence Tao started a polymath blog here, where he initiated four discussion threads (1, 2, 3 and 4) on deterministic ways to find primes (I’m not quite sure how that’s proceeding — […]
Pingback by Polymath again « What Is Research? — October 26, 2009 @ 10:44 pm |
Hate to be boring about it, but you can attain deterministic time bound O(10^(k/2 + o(1))), the same time
bound you got, by simply sieving an array that many bits long. You need the RH to assure that any this-size region will contain a prime, however. All multiples of numbers up to this bound, are removed by the sieving.
Well, you probably already thought of that. (I don’t know how to use this blog thing to tell what happened before. Where’s the how-to guide?) Sure is low-tech.
As another comment, I’m not sure this whole topic has much interest. To explain, we have easy randomized algorithms that will do the job in polynomial(k) time with high probability. These algorithms are very very very simple. Any deterministic algorithm you invent is almost certainly, by comparison, going to be utterly worthless, way more complicated and slower. That’s the first problem. The second problem is, suppose I derandomize that algorithm by simply using certain deterministic pseudorandom number generators (I have some which I can prove, starting from a random seed, will pass every possible polytime statistical test provided that ANY generator exists that does… furthermore I can prove they are nearly as immune to randomness tests as it is possible for any algorithm to be…). So, in that case, I’ve solved your problem OR there exists no such pseudo-random number generator. So in the event I haven’t solved your problem, a way, way, way more important and profound result is at hand. And very weak randomness properties are required in your application.
So all this suggests to me, that this was a fairly stupid problem to choose.
Mind you, I won’t say it’s totally stupid since I admit it would feel interesting to know the answer to your problem. It’s kind of like the AKS primality test was allegedly a great development… and yes it was in some sense… but from a practical point of view, it is a total waste of time.
My final comment is: are you aware of the following papers?
Janos Pintz, William L. Steiger, Endre Szemeredi: Two Infinite Sets of Primes with Fast Primality Tests,
STOC 1988 pp 504-509, journal version is
Maths of Computation Vol. 53, No. 187, July 1989 pp.399-406.
Eric Bach: How to Generate Factored Random Numbers, SIAM J. Computing 17 (1988) pp.179-193
These were done pre-AKS, but are better than AKS for many purposes of your ilk.
Comment by Warren D Smith (PhD) — May 8, 2011 @ 11:48 pm |
1 мар 2011 Коль скоро вы крыться придерживаться годной вам диеты в пользу кого ума, ваш ум довольно заниматься почти максимальной отдачей вплоть до
Диетическое и лечебное питание при различных заболеваниях.
диеты, как похудеть, упражнения, фитнес, красивая фигура, гадания.
27 май 2011 Диета Пьера Дюкана во Франции неимоверно популярна. Но не все так розово, Диеты бывают разные – гипокалорийные, белковые и… счастливые.
Диетическое питание. Средства для похудения, диеты, похудеть быстро. Советы и рекомендации.
Comment by Lincidoro — July 15, 2011 @ 10:11 pm |