The previous research thread for the Polymath7 project “the Hot Spots Conjecture” is now quite full, so I am now rolling it over to a fresh thread both to summarise the progress thus far, and to make it a bit easier to catch up on the latest developments.
The objective of this project is to prove that for an acute angle triangle ABC, that
- The second eigenvalue of the Neumann Laplacian is simple (unless ABC is equilateral); and
- For any second eigenfunction of the Neumann Laplacian, the extremal values of this eigenfunction are only attained on the boundary of the triangle. (Indeed, numerics suggest that the extrema are only attained at the corners of a side of maximum length.)
To describe the progress so far, it is convenient to draw the following “map” of the parameter space. Observe that the conjecture is invariant with respect to dilation and rigid motion of the triangle, so the only relevant parameters are the three angles of the triangle. We can thus represent any such triangle as a point
in the region
. The parameter space is then the following two-dimensional triangle:
Thus, for instance
- A,N,P represent the degenerate obtuse triangles (with two angles zero, and one angle of 180 degrees);
- B,F,O represent the degenerate acute isosceles triangles (with two angles 90 degrees, and one angle zero);
- C,E,G,I,L,M represent the various permutations of the 30-60-90 right-angled triangle;
- D,J,K represent the isosceles right-angled triangles (i.e. the 45-45-90 triangles);
- H represents the equilateral triangle (i.e. the 60-60-60 triangle);
- The acute triangles form the interior of the region BFO, with the edges of that region being the right-angled triangles, and the exterior being the obtuse triangles;
- The isosceles triangles form the three line segments NF, BP, AO. Sub-equilateral isosceles triangles (with apex angle smaller than 60 degrees) comprise the open line segments BH,FH,OH, while super-equilateral isosceles triangles (with apex angle larger than 60 degrees) comprise the complementary line segments AH, NH, PH.
Of course, one could quotient out by permutations and only work with one sixth of this diagram, such as ABH (or even BDH, if one restricted to the acute case), but I like seeing the symmetry as it makes for a nicer looking figure.
Here’s what we know so far with regards to the hot spots conjecture:
- For obtuse or right-angled triangles (the blue shaded region in the figure), the monotonicity results of Banuelos and Burdzy show that the second claim of the hot spots conjecture is true for at least one second eigenfunction.
- For any isosceles non-equilateral triangle, the eigenvalue bounds of Laugesen and Siudeja show that the second eigenvalue is simple (i.e. the first part of the hot spots conjecture), with the second eigenfunction being symmetric around the axis of symmetry for sub-equilateral triangles and anti-symmetric for super-equilateral triangles.
- As a consequence of the above two facts and a reflection argument found in the previous research thread, this gives the second part of the hot spots conjecture for sub-equilateral triangles (the green line segments in the figure). In this case, the extrema only occur at the vertices.
- For equilateral triangles (H in the figure), the eigenvalues and eigenfunctions can be computed exactly; the second eigenvalue has multiplicity two, and all eigenfunctions have extrema only at the vertices.
- For sufficiently thin acute triangles (the purple regions in the figure), the eigenfunctions are almost parallel to the sector eigenfunction given by the zeroth Bessel function; this in particular implies that they are simple (since otherwise there would be a second eigenfunction orthogonal to the sector eigenfunction). Also, a more complicated argument found in the previous research thread shows in this case that the extrema can only occur either at the pointiest vertex, or on the opposing side.
So, as the figure shows, there has been some progress on the problem, but there are still several regions of parameter space left to eliminate. It may be possible to use perturbation arguments to extend validity of the hot spots conjecture beyond the known regions by some quantitative extent, and then use numerical verification to finish off the remainder. (It appears that numerics work well for acute triangles once one has moved away from the degenerate cases B,F,O.)
The figure also suggests some possible places to focus attention on, such as:
- Super-equilateral acute triangles (the line segments DH, GH, KH). Here, we know the second eigenfunction is simple (and anti-symmetric).
- Nearly equilateral triangles (the region near H). The perturbation theory for the equilateral triangle could be non-trivial due to the repeated eigenvalue here.
- Nearly isosceles right-angled triangles (the regions near D,G,K). Again, the eigenfunction theory for isosceles right-angled triangles is very explicit, but this time the eigenvalue is simple and perturbation theory should be relatively straightforward.
- Nearly 30-60-90 triangles (the regions near C,E,G,I,L,M). Again, we have an explicit simple eigenfunction in the 30-60-90 case and an analysis should not be too difficult.
There are a number of stretching techniques (such as in the Laugesen-Siudeja paper) which are good for controlling how eigenvalues deform with respect to perturbations, and this may allow us to rigorously establish the first part of the hot spots conjecture, at least, for larger portions of the parameter space.
As for numerical verification of the second part of the conjecture, it appears that we have good finite element methods that seem to give accurate results in practice, but it remains to find a way to generate rigorous guarantees of accuracy and stability with respect to perturbations. It may be best to focus on the super-equilateral acute isosceles case first, as there is now only one degree of freedom in the parameter space (the apex angle, which can vary between 60 and 90 degrees) and also a known anti-symmetry in the eigenfunction, both of which should cut down on the numerical work required.
I may have missed some other points in the above summary; please feel free to add your own summaries or other discussion below.

[…] has been some progress in the polymath 7 project. See the new thread here. Like this:LikeBe the first to like this […]
Pingback by New thread for Polymath 7 « Euclidean Ramsey Theory — June 12, 2012 @ 10:00 pm |
Here is a simple eigenvalue comparison theorem: if denotes the Neumann eigenvalues of a domain D (counting multiplicity), and
denotes the Neumann eigenvalues of a domain D (counting multiplicity), and  is a linear transformation, then
is a linear transformation, then
for each k. This is because of the Courant-Fisher minimax characterisation of as the supremum of the infimum of the Rayleigh-Ritz quotient
as the supremum of the infimum of the Rayleigh-Ritz quotient  over all codimension k subspaces of
over all codimension k subspaces of  , and because any candidate
, and because any candidate 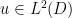 for the Rayleigh-Ritz quotient on D can be transformed into a candidate
for the Rayleigh-Ritz quotient on D can be transformed into a candidate 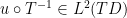 for the Rayleigh-Ritz quotient on TD, and vice versa. (This is not the most sophisticated comparison theorem available – for instance, the Laugesen-Siudeja paper has a more delicate analysis involving comparison of one triangle against two reference triangles, instead of just one – but it is one of the easiest to state and prove.)
for the Rayleigh-Ritz quotient on TD, and vice versa. (This is not the most sophisticated comparison theorem available – for instance, the Laugesen-Siudeja paper has a more delicate analysis involving comparison of one triangle against two reference triangles, instead of just one – but it is one of the easiest to state and prove.)
One corollary of this theorem is that if one has a spectral gap for some triangle D, then this spectral gap persists for all nearby triangles TD, as long as T has condition number less than
for some triangle D, then this spectral gap persists for all nearby triangles TD, as long as T has condition number less than  . This should allow us to start rigorously verifying the simplicity of the eigenvalue for at least some of the regions of the above figure, and in particular in the vicinity of the points C,D,E,G,I,J,K,L,M where the eigenvalues are explicit. With numerics, we should be able to cover other areas as well, except in the vicinity of the equilateral triangle H where of course we have a repeated eigenvalue, but perhaps some perturbative analysis near that triangle can establish simplicity there too.
. This should allow us to start rigorously verifying the simplicity of the eigenvalue for at least some of the regions of the above figure, and in particular in the vicinity of the points C,D,E,G,I,J,K,L,M where the eigenvalues are explicit. With numerics, we should be able to cover other areas as well, except in the vicinity of the equilateral triangle H where of course we have a repeated eigenvalue, but perhaps some perturbative analysis near that triangle can establish simplicity there too.
Comment by Terence Tao — June 12, 2012 @ 10:50 pm |
Stability of Neumann eigenvalues was studied by Banuelos and Pang (Electron. J. Diff. Eqns., Vol. 2008(2008), No. 145, pp. 1-13) and Pang (http://dx.doi.org/10.1016/j.jmaa.2008.04.026). They prove that multiplicity 1 is stable under small perturbations, while multiplicity 2 is not. Hence linear transformation above can be replaced with almost any small perturbation.
Comment by Bartlomiej Siudeja — June 12, 2012 @ 11:41 pm |
And a small last name correction: Siujeda should really be Siudeja. Here and in the main summary. [Oops! Sorry about that. Corrected, -T.]
Comment by Bartlomiej Siudeja — June 12, 2012 @ 11:46 pm |
Joe and I have a working high-order finite element code (to give increased order of approximation as we increase the resolution) . We’re working on a mapped domain (as described in a different thread), and are starting to explore the parameter space you suggested.
So far, no surprises, though we haven’t reached the perturbed equilateral triangle. We hope to post some results and graphics soon. Visualizing the results is taking some thought: for each point in parameter space, we want to record: whether the conjecture holds for the approximation; the approximate eigenvalue(s); the spectral gap; and some measure of the quality of the approximation.
Comment by Nilima Nigam — June 13, 2012 @ 4:25 am |
Just a note: The rigorous numerical approach from [FHM1967] was used extensively to study eigenvalues of triangles by Pedro Antunes and Pedro Freitas. They studied various aspects of the Dirichlet spectrum using improvement of [FHM1967] due to Payne and Moler (http://www.jstor.org/stable/2949550). This method also works extremely well with bessel functions, even for far from degenerate triangles.
Comment by Bartlomiej Siudeja — June 12, 2012 @ 10:55 pm |
The Fox, Henrici and Moler paper is beautiful, and was updated by Betcke and Trefethen in SIAM Review in 2005. Barnett has a more recent paper discussing the method of particular solutions, based on Bessel functions, applied to the Neumann problem. This is harder, and the numerics are more challenging:
Comment by Nilima Nigam — June 13, 2012 @ 4:30 am |
Continuing the ideas for Comments 13,14, and 18 of the previous thread,
Consider a super-equilateral isosceles triangle (I will call it a 50-50-80 triangle to make things clear). As discussed in Comment 14 and 18, since we know the second eigenfunction is anti-symmetric we can instead consider the 40-50-90 right triangle with mixed Dirichlet-Neumann.
Two comments/ideas:
-It should also be that we can now “unfold” the 40-50-90 triangle into a 40-40-100 triangle with mixed Dirichlet-Neumann and, intuitively at least, it should be the case that the first non-trivial eigenfunction there is the eigenfunction we are looking for (Though while I think that “folding in” is always legal, appealing to the Raleigh-Ritz formalism, in general “folding out” might introduce new first-non-trivial eigenfunctions). I am not sure if this really buys us anything though…
-Having reduced the problem to the Dirichlet-Neumann boundary case, maybe it is possible to implement the method of particular solutions as suggested by Nilima in Comment 13 (links provided there). The method of particular solutions, at least as presented in those papers, considered a Dirichlet boundary condition that an eigenfunction was chosen to try and match. For the mixed problem, we now have a Dirichlet boundary (the fact that the other two boundaries are Neumann shouldn’t matter as those are taken care of for free when choosing an eigenfunction consisting of “Fourier-Bessel” functions anchored at the opposite angle).
Comment by letmeitellyou — June 12, 2012 @ 11:48 pm |
On the first non-trivial eigenfunction for a triangle with mixed boundary conditions (two sides Neumann, and one side Dirichlet):
Intuitively, the following statement must be true for all such triangles: The maximum of the first non-trivial eigenfunction occurs at the corner opposite to the Dirichlet side.
Perhaps this is on the books somewhere? A probabilistic interpretation is as follows: The solution to the heat equation on the mixed-boundary triangle with initial condition can be expressed probabilistically as
can be expressed probabilistically as
Where is the first time that
is the first time that 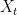 , a Brownian motion starting from
, a Brownian motion starting from  and reflected on the Neumann sides, hits the Dirichlet side. Intuitively to keep your Brownian motion alive the longest you would start it at the opposite corner.
and reflected on the Neumann sides, hits the Dirichlet side. Intuitively to keep your Brownian motion alive the longest you would start it at the opposite corner.
Of course this is all intuition and not a formal proof…
Comment by letmeitellyou — June 13, 2012 @ 12:28 am |
Probabilistic intuition is extremely convincing. In fact to make it even more appealing, think about “regular” polygon that can be built by gluing matching Neumann sides of many triangles. We get a “regular” polygon with Dirichlet boundary conditions. By rotational symmetry maximum survival time must happen at the center. Of course not every triangle gives a nice polygon (angles never add up to 2pi), and the ones we need never give one. We would need a multiple cover to make a polygon for arbitrary rational angles, but the intuition is kind of lost this way.
Comment by Bartlomiej Siudeja — June 13, 2012 @ 12:53 am |
Yah I was thinking about this as well… you would get sort of a spiral staircase no? But I think there might be some issue with defining the Brownian motion on this spiral staircase as it might flip out near the origin (i.e. it will have some crazy winding number). Although, with probability 1, the Brownian motion won’t actually hit the origin so maybe it isn’t a big deal.
On page 472 of the paper [BT2005] Timo Betcke, Lloyd N. Trefethen, Reviving the Method of Particular Solutions, they mention that how the eigenfunction for the wedge cannot be extended analytically unless an integer multiple of the angle is .
.
Comment by Chris Evans — June 13, 2012 @ 3:01 am |
Actually maybe a proof can be furnished using a synchronous coupling!
Consider a triangle with 1 side Dirichlet and 2 sides Neumann. Orient it so that it lies in the right half plane and has its Dirichlet side along the y-axis (so that the point with the largest
and has its Dirichlet side along the y-axis (so that the point with the largest  -coordinate in the triangle is the opposite corner (where we claim the hotspot is).
-coordinate in the triangle is the opposite corner (where we claim the hotspot is).
Now consider two points and
and 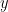 in the plane (I will abuse notation and call the points
in the plane (I will abuse notation and call the points  and
and 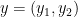 ). Now consider a synchronously-coupled reflected Brownian motion
). Now consider a synchronously-coupled reflected Brownian motion  started from these two points (Synchronously coupled means that they are driven by the same brownian motion but they might of course reflect at different times).
started from these two points (Synchronously coupled means that they are driven by the same brownian motion but they might of course reflect at different times).
If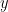 lies to the right of
lies to the right of  , it ought to be the case that always
, it ought to be the case that always 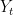 lies to the right of
lies to the right of 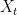 . consequently
. consequently 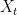 is more likely to hit the Dirichlet boundary than
is more likely to hit the Dirichlet boundary than 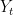 .
.
It therefore would follow that the place to start to take the longest to hit the boundary is the point furthest to the right, i.e. the opposite corner as predicted.
Notes:
-The issues with coupled Brownian motions dancing around each other should be avoided here.. in the acute triangle with all three sides Neumann this was an issue but here there is only one corner to play around/bounce off of.
-This is really stating the following monotonicity theorem: If then
then 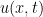 is monotonically increasing from left to right for all
is monotonically increasing from left to right for all 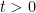 . There might be a more direct analytic proof.
. There might be a more direct analytic proof.
-Seeing as this was a very simple argument it is likely to be already known (or I could be wrong about the coupling preserving the orientation).
Comment by letmeitellyou — June 13, 2012 @ 2:53 am |
Unfortunately, I think the synchronous coupling can flip the orientation of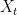 and
and 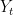 . Suppose for instance that
. Suppose for instance that 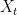 and
and 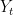 are oriented vertically, and
are oriented vertically, and 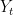 hits one of the Neumann sides oriented diagonally. Then
hits one of the Neumann sides oriented diagonally. Then 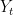 can bounce in such a way that it ends up to the left of
can bounce in such a way that it ends up to the left of 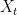 .
.
But perhaps some variant of this coupling trick should work…
Comment by Terence Tao — June 13, 2012 @ 4:13 am |
Ah, good point! The points $x$ and $y$ would have to start such that the angle between them is smaller than the angle of the opposite side… this is actually a condition in the Baneulos-Burdzy paper as well (the “left-right” formalism is just a simpler way to discuss it). But I don’t think this will be an obstacle.
I will work on writing this up more clearly
Edit: While talking in terms of all these angles is messy, the succinct explanation is:
As long as the points and
and 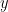 are such that the line segment connecting them is nearly horizontal (and it’s a wide range that is allowed based on the angles… basically anything from the angle you get if you ram them against the bottom line to the angle you get when you ram them against the top line), than what I wrote should hold. And that is sufficient to prove the lemma.
are such that the line segment connecting them is nearly horizontal (and it’s a wide range that is allowed based on the angles… basically anything from the angle you get if you ram them against the bottom line to the angle you get when you ram them against the top line), than what I wrote should hold. And that is sufficient to prove the lemma.
Comment by Chris Evans — June 13, 2012 @ 4:28 am |
Ok, here is a writeup which explains things more precisely
http://www.math.missouri.edu/~evanslc/Polymath/MixedTriangle
In there I only give an argument for the case that the angle opposite the Dirichlet side is acute… but I think the obtuse case should be true as well. It all boils down to whether the following probabalistic statement is true:
Consider the infinite wedge . Let
. Let  be a synchronously coupled Brownian motion starting from points
be a synchronously coupled Brownian motion starting from points  and
and 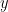 such that (thought of as elements of the complex plane),
such that (thought of as elements of the complex plane), 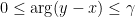 . Then
. Then  for all
for all 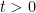 .
.
Comment by Chris Evans — June 13, 2012 @ 5:48 am |
I think this does indeed work for acute angles, so this should settle the super-equilateral isosceles case, but I’ll try to recheck the details tomorrow. I think I can also recast the coupling arguments as a PDE argument based on the maximum principle – this doesn’t add anything as far as the results are concerned, but may be a useful alternate way of thinking about these sorts of arguments. (I come from a PDE background rather than a probability one, so I am perhaps biased in this regard.)
This type of argument may also settle the non-isosceles case in regimes in which we can show that the nodal line is reasonably flat, though I don’t know how one would actually try to show that…
Comment by Terence Tao — June 13, 2012 @ 6:44 am |
OK, I wrote up both a sketch of the Brownian motion argument and the maximum principle argument on the wiki at
http://michaelnielsen.org/polymath1/index.php?title=The_hot_spots_conjecture#Isosceles_triangles
So I think we can now move super-equilateral isosceles triangles (the lines HD, HJ, HK in the above diagram) into the “done” column, thus finishing off all the isosceles cases. (Actually the argument also works for the lowest anti-symmetric mode of the sub-equilateral triangles as well, though this is not directly relevant for the hot spots conjecture.) So now we have to start braving the cases in which there is no axis of symmetry to help us…
Comment by Terence Tao — June 13, 2012 @ 4:52 pm |
I’m a bit confused about the PDE proof of Corrolary 4. In the case where lies on the interior of
lies on the interior of 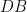 , it is correct that
, it is correct that  is parallel to
is parallel to 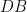 . However, we do not know what is its direction. If it has the same direction like the vector
. However, we do not know what is its direction. If it has the same direction like the vector 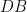 then we are OK. But if its direction is
then we are OK. But if its direction is 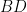 then it does not lie in the sector
then it does not lie in the sector  .
.
Comment by Hung Tran — June 13, 2012 @ 8:08 pm |
By hypothesis, at this point lies on the boundary of the region
lies on the boundary of the region 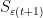 (in particular, it is not in S). The only point on this boundary that is parallel to DB is the point which is a distance
(in particular, it is not in S). The only point on this boundary that is parallel to DB is the point which is a distance  from the origin in the BD direction. (I should draw a picture to illustrate this but I was too lazy to do so for the wiki.)
from the origin in the BD direction. (I should draw a picture to illustrate this but I was too lazy to do so for the wiki.)
Comment by Terence Tao — June 13, 2012 @ 8:18 pm |
Thanks for your clarification. I got that part.
I’m still confused though. In the proof, you basically performed the reflection arguments to consider the cases when lies on the interiors of
lies on the interiors of  . By doing so,
. By doing so,  turns out to be an interior point of the domain and then it is pretty straightforward to deduce the result from classical maximum principle.
turns out to be an interior point of the domain and then it is pretty straightforward to deduce the result from classical maximum principle.
My concern is about the reflection arguments. Do you need sth like in order to do so?
in order to do so?
Comment by Hung Tran — June 14, 2012 @ 5:15 am
No, to reflect around a flat edge one only needs the Neumann condition . The second normal derivative
. The second normal derivative  will reflect in an even fashion (rather than an odd fashion) around the edge, and so does not need to vanish; it only needs to be continuous in order to obtain a C^2 reflection. Once one has a C^2 reflection, one solves the eigenfunction equation in the classical sense in the unfolded domain, and elliptic regularity in that domain upgrades the regularity to
will reflect in an even fashion (rather than an odd fashion) around the edge, and so does not need to vanish; it only needs to be continuous in order to obtain a C^2 reflection. Once one has a C^2 reflection, one solves the eigenfunction equation in the classical sense in the unfolded domain, and elliptic regularity in that domain upgrades the regularity to 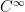 (at least as long as one stays away from the corners).
(at least as long as one stays away from the corners).
Comment by Terence Tao — June 14, 2012 @ 2:58 pm
Oh, I meant at the specific point . Your argument should be OK for eigenfunctions. But here we are dealing with the heat equations, right?
. Your argument should be OK for eigenfunctions. But here we are dealing with the heat equations, right?
In general, I think it would be really interesting to consider the heat equation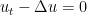 in
in  with the given initial data
with the given initial data 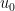 chosen in such a way that it is increasing along some specific directions. Let say
chosen in such a way that it is increasing along some specific directions. Let say 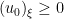 for some unit vector
for some unit vector 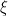 . If we can use maximum principle to show that
. If we can use maximum principle to show that  by essentially killing the boundary cases then we are done.
by essentially killing the boundary cases then we are done.
Comment by Hung Tran — June 14, 2012 @ 4:13 pm
Ah, fair enough, but even when reflecting a solution to the heat equation rather than an eigenfunction, one still gets a classical (C^2 in space, C^1 in time) solution to the heat equation on reflection as long as the Neumann boundary condition is satisfied (and providing that the original solution was already C^2 up to the boundary, which I believe can be established rigorously in the acute triangle case), and then by applying parabolic regularity instead of elliptic regularity one can ensure that this is a smooth solution. (Alternatively, one can unfold the triangle around the edge of interest at time zero, solve the heat equation with Neumann data on the unfolded kite region, and then use the uniqueness theory of the heat equation to argue that this solution is necessarily symmetric around the edge of unfolding, and that the restriction to the original triangle is the original solution to the heat equation.)
Comment by Terence Tao — June 14, 2012 @ 4:26 pm
Oh, thank you. Probably now I see my source of confusion. Probable one needs on
on 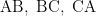 in order to get higher regularity when reflecting. I was confused about this part.
in order to get higher regularity when reflecting. I was confused about this part.
So why don’t we proceed by considering the heat equation with Neumann boundary condition in with given initial date $u_0$ satisfying sth like
with given initial date $u_0$ satisfying sth like  on
on 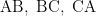 and
and 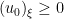 for some unit direction $\xi$. If we then let
for some unit direction $\xi$. If we then let  then
then  solves also the heat equation. We want to show that
solves also the heat equation. We want to show that 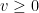 or so by using maximum principle. As we know,
or so by using maximum principle. As we know, ![\max_{{\rm ABC} \times [0,T]} v = \max \{ \max_{\rm{ABC}} (u_0)_\xi, \max_{\rm{AB,BC,CA} \times (0,T)} v\}](https://s0.wp.com/latex.php?latex=%5Cmax_%7B%7B%5Crm+ABC%7D+%5Ctimes+%5B0%2CT%5D%7D+v+%3D+%5Cmax+%5C%7B+%5Cmax_%7B%5Crm%7BABC%7D%7D+%28u_0%29_%5Cxi%2C+%5Cmax_%7B%5Crm%7BAB%2CBC%2CCA%7D+%5Ctimes+%280%2CT%29%7D+v%5C%7D&bg=ffffff&fg=000000&s=0&c=20201002) . And since one can omit the boundary cases by performing reflection method, it should be OK.
. And since one can omit the boundary cases by performing reflection method, it should be OK.
Comment by Hung Tran — June 14, 2012 @ 6:24 pm
I have done some computations to support my argument above. The point now is to build a function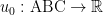 so that
so that  on the edges and
on the edges and 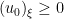 for some unit vector $\xi$. Then
for some unit vector $\xi$. Then  inherits this monotonicity property of
inherits this monotonicity property of 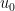 , namely
, namely  in
in  .
.
Here is the first computation in case is an acute isosceles triangle like in Corollary 4. Let’s assume
is an acute isosceles triangle like in Corollary 4. Let’s assume 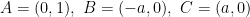 for some
for some 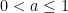 . Then we can build
. Then we can build 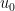 which is antisymmetric around
which is antisymmetric around  as
as  . It turns out that $(u_0)_x, \nabla u \cdot (\frac{1}{a},1) \ge 0$ for
. It turns out that $(u_0)_x, \nabla u \cdot (\frac{1}{a},1) \ge 0$ for 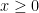 . This is exactly the needed function for Corollary 4.
. This is exactly the needed function for Corollary 4.
I will try to build such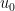 for general acute triangle to see if the shape of
for general acute triangle to see if the shape of  has anything to do with the direction
has anything to do with the direction 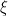 . It may then help us to see where the min and the max of the second eigenfunctions locate.
. It may then help us to see where the min and the max of the second eigenfunctions locate.
Comment by Hung Tran — June 15, 2012 @ 4:33 am
Great! Actually, half of my graduate thesis was on reflected Brownian motion and the other half was on maximum principles for systems… so it is cool to see that they are related.
And on a more practical note, rigorously arguing the geometric properties of coupled Brownian motion can be a bit of a mess (involving Ito’s formula) so if it can be avoided by appealing to the maximum principle, so much the better.
Comment by Chris Evans — June 13, 2012 @ 9:51 pm |
After a night’s rest, I think the statement I made above about “the infinite wedge preserving the angle” only holds true in the acute case. For the obtuse case, it isn’t to hard to see how the angle won’t always be preserved.
It still seems it should be the case that the first eigenfunction for the mixed triangle should be at the vertex opposite the Dirichlet side… but at this point I suppose we only need to know the acute case.
Edit: Actually I think the obtuse case might follow from the following paper by Mihai Pascu which uses an exotic “scaling coupling” to prove Hot-Spots results for convex domains which are symmetric about one axis.
convex domains which are symmetric about one axis.
http://www.ams.org/journals/tran/2002-354-11/S0002-9947-02-03020-9/home.html
Reflecting the triangle across its Dirichlet side would give such a domain provided that we could “smooth out the corners” without affecting the eigenfunction too much.
Comment by Chris Evans — June 13, 2012 @ 9:48 pm |
Chris, I am not sure this is pertinent to your argument. But the regularity of the eigenfunctions for the mixed Dirichlet-Neumann case must degenerate, as the angle between the Dirichlet and Neumann sectors becomes near pi. To see this, think about a sector of a circle with Dirichlet data on one ray and the curvilinear arc, and Neumann on the remaining ray. The solution (by seperation of variables) is again in terms of Bessel functions, but this time with fractional order. As long as the angle of the sector is less than pi, a reflection about the Neumann side would give you an eigenfunction problem with Dirichlet data, and you pick out the one with the right symmetry.
However, as the interior angle approached pi, after reflection the doubled sector gets closer to the circle with a slit. The resulting eigenfunction is not smooth.
This argument suggests that if, after reflections, you have a mixed boundary eigenproblem where the Dirichlet-Neumann segments are meeting at nearly flat angles, then there may be issues.
Comment by Nilima Nigam — June 13, 2012 @ 3:08 pm |
Well, for our application the Dirichlet-Neumann region of interest is a folded super-equilateral triangle, so one of the angles between Dirichlet and Neumann is a right angle (thus becomes not an angle at all when unfolded) and the other is between 30 and 45 degrees, so the regularity looks pretty good (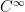 at the right angle,
at the right angle,  at the less-than-45-degree-angle, and
at the less-than-45-degree-angle, and  at the remaining angle between the two Neumann edges, which is less than 60 degrees. (From Bessel function expansion in a Neumann triangle we know that eigenfunctions have basically
at the remaining angle between the two Neumann edges, which is less than 60 degrees. (From Bessel function expansion in a Neumann triangle we know that eigenfunctions have basically 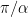 degrees of regularity at an angle of size
degrees of regularity at an angle of size  , and are
, and are 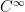 when
when 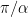 is an integer. I think the same should also be true for solutions to the heat equation with reasonable initial data, though I didn’t check this properly.)
is an integer. I think the same should also be true for solutions to the heat equation with reasonable initial data, though I didn’t check this properly.)
But, yes, things are probably more delicate once the Dirichlet-Neumann angles get obtuse. In the case when the Dirichlet boundary comes from a nodal line from a Neumann eigenfunction, the Dirichlet boundary should hit the Neumann boundary at right angles (unless it is in a corner or is somehow degenerate), so this should not be a major difficulty.
Comment by Terence Tao — June 13, 2012 @ 3:51 pm |
Hmm… it seems that we have shown that for a triangle with mixed boundary conditions (one side Dirichlet, two sides Neumann), that the extremum of the first eigenfunction lies at the vertex opposite the Dirichlet side, provided that angle is acute.
Such a triangle could have that the angle between the Dirichlet side and one of the Neumann sides is arbitrarily close to … but things should still be ok (provided what I wrote in the previous paragraph is true).
… but things should still be ok (provided what I wrote in the previous paragraph is true).
In your example, you have two sides which are Dirichlet and only one side which is Neumann… maybe that is what makes the difference?
Comment by Chris Evans — June 13, 2012 @ 9:56 pm |
Chris, I tried the case where there where two Neumann sides and one Dirichlet. Same problem- but my argument is for a mixed problem where the junction angle is nearing pi. As Terry points out, this concern may not arise for the argument you are trying.
Comment by Nilima Nigam — June 14, 2012 @ 3:55 am |
We’re exploring the parameter space corresponding to the region BDO in the triangle above. We’re taking a set of discrete points in this parameter set, and verifying the conjecture as well as computing the spectral gap for the corresponding domain . To debug, we’re taking a coarse spacing of pi/10 in each direction, but we will refine this. We’re using piecewise quadratic polynomials in an H^1 conforming finite element method, with Arnoldi iterations with shift to get the smaller eigenvalues.
I have a quick question- is there some target spacing you’d like? This will influence some memory management issues.
Comment by Nilima Nigam — June 13, 2012 @ 10:01 pm |
Hmm, good question. As a test case for a back-of-the-envelope calculation, let’s look at the range of stability for the isosceles right-angled (i.e. 45-45-90) triangle (point D in the diagram), say with vertices (0,0), (1,0), (1,1) for concreteness. This is half of the unit square and so the Neumann eigenvalues can in fact be read off quite easily by Fourier series. The second eigenvalue is , with eigenfunction
, with eigenfunction  , and then there is a third eigenvalue at
, and then there is a third eigenvalue at 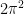 with eigenfunction
with eigenfunction 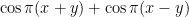 . So, by Comment 2, the second eigenvalue remains simple for all linear images TD of this triangle with condition number less than
. So, by Comment 2, the second eigenvalue remains simple for all linear images TD of this triangle with condition number less than  . To convert the 45-45-90 triangle into another right-angled triangle
. To convert the 45-45-90 triangle into another right-angled triangle  triangle for some
triangle for some 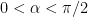 requires a transformation of condition number
requires a transformation of condition number 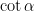 , which lets one obtain simplicity of eigenvalues for such triangles whenever
, which lets one obtain simplicity of eigenvalues for such triangles whenever  , or about 35 degrees – enough to get about two thirds of the way from point D on the diagram to point C. This extremely back of the envelope calculation suggests that increments of about 10 degrees (or about
, or about 35 degrees – enough to get about two thirds of the way from point D on the diagram to point C. This extremely back of the envelope calculation suggests that increments of about 10 degrees (or about 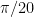 ) at a time might be enough to get a good resolution. But things may get worse as one approaches the equilateral triangle (point H) or the degenerate triangle (points B, F, O).
) at a time might be enough to get a good resolution. But things may get worse as one approaches the equilateral triangle (point H) or the degenerate triangle (points B, F, O).
By permutation symmetry it should be enough to explore the triangle BDH instead of BDO. The Laugesen-Suideja paper at http://arxiv.org/abs/0907.1552 has some figures on eigenvalues in the isosceles case (Fig 2 and Fig 3) that could be used for comparison.
Comment by Terence Tao — June 13, 2012 @ 10:37 pm |
thanks, this is helpful. I’ll set this running with pi/50, to be on the safe side. This will take a few hours to run.
certainly the numerics suggest that the manner in which I approach the point for the equilateral triangle impacts the spectral gap. however, the resolution is not sharp enough to make this formal.
Comment by Nilima Nigam — June 13, 2012 @ 11:17 pm |
A detail which will not affect any analytical attack, but which should be noted for anyone else doing numerics on this.
As we search through parameter space, we look at what happens with a triangle with given edges – but we should probably fix one side, so we can compare eigenvalues. This is important since what we also want to examine is the spectral gap.
Joe and I’ve fixed one side of the acute triangle to have length 1. As we range through parameter space, the other sides, and the area of the triangles, change. We are recording this information.
May I recommend that if anyone else is doing numerics on this problem, they also make available the area of the triangles used (or at least one side) for each choice of angles? This way, we’ll be able to compare eigenvalues on triangles with the same angles.
Comment by Nilima Nigam — June 14, 2012 @ 4:07 am |
I think i can show that second eigenfunction is simple. It involves a few not-overly complicated cases of comparisons between a given triangle and a few known cases (through linear mappings). There seems to be a way to do all of this using one very complicated comparison (with 4-5 reference triangles) and an extremely ugly upper bound for acute triangles (many pages to write it down), but that is probably not worth pursuing. I will try to write something tonight, at least one simple case. It appears that even around equilateral everything should be OK.
Comment by Bartlomiej Siudeja — June 13, 2012 @ 10:18 pm |
Here is a very rough write-up of just one case containing equilateral, right isosceles, and some non-isosceles cases. I am sure this case can be optimized to include larger area. Another 3-4 cases and all triangles should be covered. I will try to optimize the approach before I post all the cases. Near the end of the argument there is an ugly inequality involving triangle parametrization. It should reduce to polynomial inequality, so in the worst case we can evaluate a few (or a bit more) points and find rough gradient estimates.
Click to access simple.pdf
Comment by Bartlomiej Siudeja — June 14, 2012 @ 2:25 am |
I was playing with reference triangles a bit more, and it seems that one case with 3 reference triangles (near equilateral) and another with just 2 (near degenerate cases) should be enough to cover all acute triangles. Details to follow.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 3:06 pm |
Great news! In addition to resolving one part of the hot spots conjecture, I think having a rigorous lower bound on the spectral gap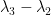 will also be useful for perturbation arguments if we are to try to verify things by rigorous numerics.
will also be useful for perturbation arguments if we are to try to verify things by rigorous numerics.
Comment by Terence Tao — June 15, 2012 @ 1:26 am |
This thread is getting somewhat large!
I’d posted some of this information below, but this may be useful. A plot of the spectral gap for the approximated eigenvalues, \lambda_3-\lambda_2 multiplied by the area of the triangle \Omega as we range through parameter space is here:

Comment by Nilima Nigam — June 15, 2012 @ 1:48 am |
The simplest proof that eigenvalue is simple will have almost no gap bound. However, if one wants to get something for a specific triangle, one can use very complicated comparisons and upper bounds without much trouble. In particular upper bound can include 3 or more known eigenfunctions. Except that even with just 2 eigenfunctions there is no way to write down the result from Rayleigh quotient for the test function on general triangle without using many pages. This is obviously not a problem for a specific triangle. The Mathematica package I mentioned in 12 was written specifically for those really ugly test function.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 2:26 am |
In comment thread 4, Terry suggested looking at the nodal line for more arbitrary triangles, which would then divide the triangle into two mixed domains.
Running computer simulations (but only for the graphs as I am not setup to do more accurate numerical approximation), it seems that the nodal line is always near the sharpest corner. Perhaps it is even close to an arc? So then that mixed-boundary sub-domain might be handled by arguments similar to those in comment thread 4. But I am not sure what we would do on the other sub-domain as it would have a strange geometry…
as I am not setup to do more accurate numerical approximation), it seems that the nodal line is always near the sharpest corner. Perhaps it is even close to an arc? So then that mixed-boundary sub-domain might be handled by arguments similar to those in comment thread 4. But I am not sure what we would do on the other sub-domain as it would have a strange geometry…
A related question: Rather than divide into sub-domains by the nodal line, is it possible to divide with respect to another level curve, say ? This would lead to the mixed boundary condition with Neumann boundary on some sides and “
? This would lead to the mixed boundary condition with Neumann boundary on some sides and “ ” on some sides… but presumably the behavior of the heat flow on that region is the same as the mixed-Dirichlet-Neumann boundary heat flow after you subtract off the constant function
” on some sides… but presumably the behavior of the heat flow on that region is the same as the mixed-Dirichlet-Neumann boundary heat flow after you subtract off the constant function  .
.
Comment by Chris Evans — June 13, 2012 @ 10:30 pm |
It may be easier to show that the extremum occurs at the sharpest corner than it is to figure out what happens to the other extremum (this was certainly my experience with the thin triangle case). See for instance Corollary 1(ii) of the Atar-Burdzy paper http://webee.technion.ac.il/people/atar/lip.pdf which establishes the extremising nature of the pointy corner for a class of domains that includes for instance parallelograms.
Once one considers level sets of eigenfunctions at heights other than 0, I think a lot less is known. For instance, the Courant nodal theorem tells us that the nodal line of a second eigenfunction is a smooth curve that bisects the domain into two regions, but this is probably false once one works with other level sets (though, numerically, it seems to be valid for acute triangles).
of a second eigenfunction is a smooth curve that bisects the domain into two regions, but this is probably false once one works with other level sets (though, numerically, it seems to be valid for acute triangles).
Comment by Terence Tao — June 13, 2012 @ 10:45 pm |
There is a paper of Burdzy at http://arxiv.org/pdf/math/0203017.pdf devoted to the study of the nodal line in regions such as triangles, with the main tool being mirror couplings; I haven’t digested it, but it does seem quite relevant to this strategy.
Comment by Terence Tao — June 14, 2012 @ 4:51 pm |
I’ve been looking at the stability of eigenvalues/eigenfunctions with respect to perturbations, and it seems that the first Hadamard variation formula is the way to go.
A little bit of setup. Following the notation on the wiki, we perturb off of a “reference” triangle to a nearby triangle
to a nearby triangle 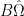 , where B is a linear transformation close to the identity. The second eigenfunction on
, where B is a linear transformation close to the identity. The second eigenfunction on  can be pulled back to a mean zero function on
can be pulled back to a mean zero function on  which minimizes the modified Rayleigh quotient
which minimizes the modified Rayleigh quotient
amongst mean zero functions, where is a symmetric perturbation of the identity matrix; this function then obeys the modified eigenvalue equation
is a symmetric perturbation of the identity matrix; this function then obeys the modified eigenvalue equation
with boundary condition .
.
Now view B = B(t) as deforming smoothly in time with B(0)=I, then M also deforms smoothly in time with M(0)=I. As long as the second eigenvalue of the reference triangle is simple, I believe one can show that and
and  will also vary smoothly in time (after normalizing
will also vary smoothly in time (after normalizing  to have norm one). One can then solve for the derivatives
to have norm one). One can then solve for the derivatives  at time zero by differentiating the eigenvalue equation and the boundary condition. What one gets is the first variation formulae
at time zero by differentiating the eigenvalue equation and the boundary condition. What one gets is the first variation formulae
and
subject to the inhomogeneous Neumann boundary condition
where is the projection to the orthogonal complement of
is the projection to the orthogonal complement of 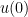 (and to
(and to  ) and
) and 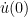 is also constrained to this orthogonal complement.
is also constrained to this orthogonal complement.
I think that by using C^2 bounds on the reference eigenfunction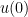 , one should then be able to obtain
, one should then be able to obtain 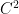 bounds on the derivative
bounds on the derivative 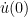 , though there is of course a deterioration if the spectral gap
, though there is of course a deterioration if the spectral gap  goes to zero. But this stability in C^2 norm should be enough to show, for instance, that if one has a reference triangle in which the second eigenfunction is simple and only has extrema in the vertices, then any sufficiently close perturbation of this triangle will also have this property. (Note from Bessel function expansion that if an extrema occurs at an acute vertex, then the Hessian is definite at that vertex, and so for any small C^2 perturbation of that eigenfunction, the vertex will still be the local extremum.) Thus, for instance, we should now be able to get the hot spots conjecture in some open neighborhood of the open intervals BD and DH (and similarly for permutations). Furthermore it should be possible to quantify the size of this neighborhood in terms of the spectral gap.
goes to zero. But this stability in C^2 norm should be enough to show, for instance, that if one has a reference triangle in which the second eigenfunction is simple and only has extrema in the vertices, then any sufficiently close perturbation of this triangle will also have this property. (Note from Bessel function expansion that if an extrema occurs at an acute vertex, then the Hessian is definite at that vertex, and so for any small C^2 perturbation of that eigenfunction, the vertex will still be the local extremum.) Thus, for instance, we should now be able to get the hot spots conjecture in some open neighborhood of the open intervals BD and DH (and similarly for permutations). Furthermore it should be possible to quantify the size of this neighborhood in terms of the spectral gap.
This argument doesn’t quite work for perturbations of the equilateral triangle H due to the repeated eigenvalue, but I think some modification of it will.
EDIT: I think the equilateral case is going to be OK too. The variation formulae will control the portion of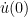 in the complement of the second eigenspace nicely, and so one can write the second eigenfunction of a perturbed equilateral triangle (after changing coordinates back to the reference triangle) as the sum of something coming from the second eigenspace of the original equilateral triangle, plus something small in C^2 norm. I think there is enough “concavity” in the second eigenfunctions of the original equilateral triangle that one can then ensure that for any sufficiently small perturbation of that triangle, the second eigenfunction only has extrema at the vertices. Will try to write up details on the wiki later.
in the complement of the second eigenspace nicely, and so one can write the second eigenfunction of a perturbed equilateral triangle (after changing coordinates back to the reference triangle) as the sum of something coming from the second eigenspace of the original equilateral triangle, plus something small in C^2 norm. I think there is enough “concavity” in the second eigenfunctions of the original equilateral triangle that one can then ensure that for any sufficiently small perturbation of that triangle, the second eigenfunction only has extrema at the vertices. Will try to write up details on the wiki later.
Comment by Terence Tao — June 14, 2012 @ 4:21 pm |
Using raw numerics (the finer-resolution calculation is not yet done), here is what I observe:
one can perturb from the equilateral triangle in a symmetric way, ie, by changing one angle by and the others by
and the others by  Or one can perturb each angle differently. The spectral gap changes rather differently, depending on how one perturbs.
Or one can perturb each angle differently. The spectral gap changes rather differently, depending on how one perturbs.
I should revisit these calculations by scaling by the Jacobian of the mapping B of the domain in each case (following the Courant spectral gap result).
Comment by Nilima Nigam — June 14, 2012 @ 6:03 pm |
Here are some graphics, to explore the parameter region (BDH) above. To enable visualization, I’m plotting data as functions of the $lateex (\alpha,\beta)$. I’m taking a rectangular grid oriented with the sides BD and DH, with 25 steps in each direction. So there are (25)^5 grid points.
Each parameter (alpha,beta,gamma) yields a triangle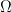 . I’m fixing one side to be of unit length. For details, please see the wiki.
. I’m fixing one side to be of unit length. For details, please see the wiki.
For each triangle, the second Neumann eigenvalue and third eigenvalue (first and second non-zero Neumann eigenvalue) is computed. I also kept track of where max|u| occurs, where u is the second eigenfunction. This is because numerically I can get either u or -u. I
A plot of the 2nd Neumann eigenvalue as we range through parameter space is here: http://www.math.sfu.ca/~nigam/polymath-figures/Lambda2.jpg
A plot of the 3rdd Neumann eigenvalue as we range through parameter space is here: http://www.math.sfu.ca/~nigam/polymath-figures/Lambda3.jpg
A plot of the spectral gap, \lambda_3-\lambda_2 multiplied by the area of the triangle \Omega as we range through parameter space is here:

One sees that the eigenvalues vary smoothly in parameter space, and that the spectral gap is largest for acute triangles without particular symmetries.
For each triangle, I also kept track of the physical location of max|u|. If it went to the corner (0,0), I allocated a value of 1; if it went to (1,0) I allocated a value of 2, and if it went to the third corner, I allocated 3. If the maximum was not reported to be at a corner, I put a value of 0.
show the result. Note that we obtain some values of 0 inside parameter space. Please DON”T interpret this to mean the conjecture fails. Rather, this is a signal that eigenfunction is likely flattening out near a corner, and that the numerical values at points near the corner are very close.
I’m running these calculations with finer tolerances now, but it will take some hours.
Comment by Nilima Nigam — June 14, 2012 @ 8:49 pm |
Hi,
I think there may be something to do using analytic pertubation theory.
The first remark is that, using a linear diffeomorphism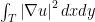 ) on a moving triangle
) on a moving triangle 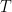 to a quadratic form
to a quadratic form that can be written
that can be written  for some symmetric matrix
for some symmetric matrix  so that
so that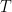 amounts to study the latter quadratic form restricted to
amounts to study the latter quadratic form restricted to  with respect to
with respect to depend analytically on a real parameter
depend analytically on a real parameter 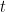 then we get a real-analytic
then we get a real-analytic
we can pullback the Dirichlet energy form (
on a fixed triangle
studying the Neumann Laplacian on
the standard Euclidean scalar product. If we now let
family in the sense of Kato-Rellich so that the eigenvalues (and eigenvectors) are organized into real-analytic branches.
Let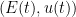 be such an analytic eigenbranch, we define the following function
be such an analytic eigenbranch, we define the following function  by
by 
 ) and suppose we can prove that this function also is analytic (that is for any choice of analytic
) and suppose we can prove that this function also is analytic (that is for any choice of analytic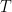 there is a Neumann eigenfunction
there is a Neumann eigenfunction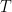 and move one of its vertices along the corresponding altitude.
and move one of its vertices along the corresponding altitude.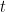 small enough the obtained triangle is obtuse. For
small enough the obtained triangle is obtuse. For 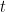 very small the second eigenbranch is simple and
very small the second eigenbranch is simple and is identically
is identically  for
for 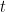 small enough and since it is analytic
small enough and since it is analytic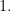 The claimed eigenfunction is the one that corresponds to this eigenbranch (because of crossings, it need not be the second one).
The claimed eigenfunction is the one that corresponds to this eigenbranch (because of crossings, it need not be the second one).
(observe that now eveything is defined on
perturbation and any corresponding eigenbranch). Then I think we can prove the following statement : “For any triangle
whose maximum is on the boundary”. The proof would be as follows. Start from your triangle
This defines an analytic perturbation and for any
satisfy the hotspot conjecture so that if we follow this particular branch, the corresponding
it is always
If we want to prove the real hotspot conjecture we can try to argue in the opposite direction : start from the second eigenvalue and follow the same perturbation.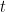 small the branch becomes simple so that it corresponds to the
small the branch becomes simple so that it corresponds to the  -th eigenvalue,
-th eigenvalue, and any
and any 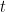 small enough the
small enough the  -th eigenfunction has its maximum on the boundary.
-th eigenfunction has its maximum on the boundary.
We now have to prove the following things :
1- For
2- For any
Of course this line of reasoning relies heavily on the analyticity of which I haven’t been able to establish yet (observe that
which I haven’t been able to establish yet (observe that  is analytic
is analytic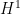 which is not good enough for
which is not good enough for 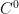 bounds). Recently I have been thinking that maybe we could instead try to prove
bounds). Recently I have been thinking that maybe we could instead try to prove means that we have removed a ball of that radius near each vertex. It should be easier to prove that
means that we have removed a ball of that radius near each vertex. It should be easier to prove that for any tobtuse triangle when we remove a ball near each vertex).
for any tobtuse triangle when we remove a ball near each vertex).
with values in
that $f_r$ is analytic where the subscript
this one is analytic (but then we need to prove something on the maximum of
I finish by pointing at two references on multiplicities in the spectrum of triangles.
First some advertisement
– Hillairet-Judge Simplicity and asymptotic separation of variables, CMP, 2011, 302(2) (Erratum, CMP, 2012, 311 (3))
– Berry-Wilkinson Diabolical points in the spectra of triangles, Proc. Roy. Soc. London, 1984, 392(1802), pp.15-43
Comment by Luc Hillairet — June 15, 2012 @ 11:57 am |
[I was editing this comment and I accidentally transferred ownership of it to myself, which is why my icon appears here. Sorry, please ignore the icon; this is Nilima’s post. – T.]
An analytic perturbation argument from known cases would certainly be great! I thought about a similar argument for the thin triangle case (http://michaelnielsen.org/polymath1/index.php?title=The_hot_spots_conjecture, under ‘thin not-quite-sectors). But I was thinking about perturbing from a sector to the triangle, and you’re thinking about perturbing from one triangle to another.
Let’s see if I follow your argument. Following the notation in (http://michaelnielsen.org/polymath1/index.php?title=The_hot_spots_conjecture, under ‘reformulation on a reference domain’), one can replace the reference triangle by any other. One then shows analyticity of the eigenvalues with respect to perturbations in the mapping B, and shows the domain of analyticity is large enough to cover all acute triangles. Is this correct?
Comment by Nilima Nigam — June 15, 2012 @ 2:59 pm |
I think it may be difficult to show analyticity of a sup norm; note that even the sup of two analytic functions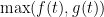 is not analytic when the two functions cross (e.g.
is not analytic when the two functions cross (e.g.  ). The enemy here is that as one varies t, a new local extremum gets created somewhere in the interior of the triangle, and eventually grows to the point where it overtakes the established extremum on the vertices, creating a non-analytic singularity in the L^infty norm.
). The enemy here is that as one varies t, a new local extremum gets created somewhere in the interior of the triangle, and eventually grows to the point where it overtakes the established extremum on the vertices, creating a non-analytic singularity in the L^infty norm.
However, I think one does have analyticity as long as the extrema are unique (up to symmetry, in the isosceles case) and non-degenerate (i.e. their Hessian is definite), and the eigenvalue is simple. This is for instance the case for the non-equilateral acute isosceles and right-angled triangles, where we know that the eigenvalues are simple and the extrema only occur at the vertices of the longest side, and a Bessel expansion at a (necessarily acute) extremal vertex shows that any extremum is non-degenerate (it looks like a non-zero scalar multiple of the 0th Bessel function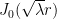 , plus lower order terms which are
, plus lower order terms which are  as
as 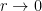 ). Certainly in this setting, the work of Banuelos and Pang ( http://eudml.org/doc/130789;jsessionid=080D9E5423278BA5ACFC818847CA97FE ) applies, and small perturbations of the triangle give small perturbations of the eigenfunction in L^infty norm at least. This (together with uniform C^2 bounds for eigenfunctions in a compact family of acute triangles, which is sketched on the wiki, and is needed to handle the regions near the vertices) is already enough to give the hot spots conjecture for sufficiently small perturbations of a right-angled or non-equilateral acute isosceles triangle.
). Certainly in this setting, the work of Banuelos and Pang ( http://eudml.org/doc/130789;jsessionid=080D9E5423278BA5ACFC818847CA97FE ) applies, and small perturbations of the triangle give small perturbations of the eigenfunction in L^infty norm at least. This (together with uniform C^2 bounds for eigenfunctions in a compact family of acute triangles, which is sketched on the wiki, and is needed to handle the regions near the vertices) is already enough to give the hot spots conjecture for sufficiently small perturbations of a right-angled or non-equilateral acute isosceles triangle.
The Banuelos-Pang results require the eigenvalue to be simple, so the perturbation theory of the equilateral triangle (in which the second eigenvalue has multiplicity 2) is not directly covered. However, it seems very likely that for any sufficiently small perturbation of the equilateral triangle, a second eigenfunction of the perturbed triangle should be close in L^infty norm to _some_ second eigenfunction of the original triangle (but this approximating eigenfunction could vary quite discontinuously with respect to the perturbation). Assuming this, this shows the hot spots conjecture for perturbations of the equilateral triangle as well, because _every_ second eigenfunction of the equilateral triangle can be shown to have extrema only at the vertices, and to be uniformly bounded away from the extremum once one has a fixed distance away from the vertices (this comes from the strict concavity of the image of the complex second eigenfunction of the equilateral triangle, discussed on the wiki).
The perturbation argument also shows that in order for the hot spots conjecture to fail, there must exist a “threshold” counterexample of an acute triangle in which one of the vertex extrema is matched by a critical point either on the edge or interior of the triangle, though it is not clear to me how to use this information.
Comment by Terence Tao — June 15, 2012 @ 3:53 pm |
Thanks ! Actually what I had in mind was trying to prove that is analytic with values in
is analytic with values in  but then I
but then I
imprudently jumped to think that this would imply the analyticity of the supnorm. So I am not sure there is something to save from the analyticity
approach I was suggesting.
Except maybe the following fact : I think that the set of triangles such that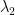 is simple is open and dense
is simple is open and dense
(and also full measure for a natural class of Lebesgue measure).
We have proved that for any mixed Dirichlet-Neumann boundary condition … except Neumann everywhere ! I have a sketch of proof
for the latter case but I never carried out the details (so there may be some bugs in the argument).
Last thing concerning analyticity of the eigenvalues and eigenfunctions, this holds only for one-parameter analytic families of triangles.
I don’t think the eigenvalues can be arranged to be analytic on the full parameter space (because there are crossings).
Comment by Luc Hillairet — June 15, 2012 @ 5:01 pm |
I would like to propose a further probabilistic intuition, based on
comment 15 of thread 1, and another
possiblity for attacking the problem. It is based on relating free
Brownian motion with reflecting Brownian motion.
If is a one dimensional Brownian motion, and we define the
is a one dimensional Brownian motion, and we define the and the zig-zag function
and the zig-zag function 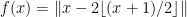 ,
, is a reflecting Brownian motion on
is a reflecting Brownian motion on ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) (as can be
(as can be of
of  in
in of
of  , write
, write
 if
if
 and note that
and note that
floor function
then
rigorously proved using stochastic calculus and local time for example) and its density
is the fundamental solution of the heat equation with Neumann boundary
conditions. To write an expression of the transition density
terms of the transition density
(1)
if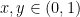 but
but
This explains why the boundary points 0 and 1 accumulate (or trap) heat at
twice the rate as interior vertices, and I believe that from here one
can conceptually prove hotspots in the very simple case of the interval.
For two dimensional reflecting Brownian motion, one needs a similar reflection . We then write the fundamental solution to the heat equation with
. We then write the fundamental solution to the heat equation with
function. To construct it: think first of an equilateral triangle
constructed as a kaleidoscope with 3 sides of equal length. Each point
inside the triangle gives rise to a lattice of points in the plane
which will be identified via the equivalence relation
Neumann boundary condition on the triangle via formula (1) for
points in the interior of the triangle. However, points at the sides
of the triangle accumulate heat at twice the rate while corner points
trap it at 6 times the rate (because the triangle is equilateral).
In general one would hope that a corner of angle alpha gets heated
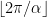 times faster
times faster
than interior points.
I think that stochastic calculus is not yet mature enough to prove to free brownian motion (lacking a multidimensional Tanaka formula). However,
to free brownian motion (lacking a multidimensional Tanaka formula). However,
that reflecting brownian motion in the triangle can be constructed by
applying the reflection
one can see if formula (1) does give the fundamental solution to the
heat equation with Neumann boundary conditions.
Comment by Gerónimo — June 14, 2012 @ 4:23 pm |
Hmm, I’m not so sure about the factor of 2 in the formula for , as this would imply that the heat kernel is discontinuous at the boundary, which I’m pretty sure is not the case. Note that the epsilon-neighbourhood of a boundary point in one dimension is only half as large as the epsilon-neighbourhood of an interior point, and so I think this factor of 1/2 cancels out the factor of 2 that one is getting from the folding coming from the zigzag function. So the heating at the endpoints is coming more from the convexity properties of the heat kernel than from folding multiplicity.
, as this would imply that the heat kernel is discontinuous at the boundary, which I’m pretty sure is not the case. Note that the epsilon-neighbourhood of a boundary point in one dimension is only half as large as the epsilon-neighbourhood of an interior point, and so I think this factor of 1/2 cancels out the factor of 2 that one is getting from the folding coming from the zigzag function. So the heating at the endpoints is coming more from the convexity properties of the heat kernel than from folding multiplicity.
Still, this does in principle give an explicit formula for the heat kernel on the triangle as some sort of infinitely folded up version of the heat kernel on something like the plane (but one may have to work instead with something more like the universal cover of a plane punctured at many points if the angles do not divide evenly into pi). One problem in the general case is that the folding map becomes dependent on the order of the edges the free Brownian motion hits, and so cannot be represented by a single map f unless one works in some complicated universal cover.
Comment by Terence Tao — June 14, 2012 @ 4:38 pm |
I agree, the formula for shouldn’t have the factor two and the
shouldn’t have the factor two and the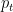 decays rapidly, endpoints with nearby
decays rapidly, endpoints with nearby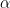 are points
are points nearby reflections.
nearby reflections.
intuition there is incorrect. However, it does suggest a new one: since
the heat kernel
reflections will accumulate more density (the notion of nearby depends on the
amount of time elapsed) and corners of angle
where there are (mainly)
Also, maybe one does not need to leave the plane since to construct the
reflecting brownian motion since two-dimensional free Brownian motion
does not visit the corners of the triangle (by polarity of countable
sets), so one only needs to keep changing the reflection edge as soon
as a new one is reached. The
transition density does indeed seem more complicated, but perhaps (1)
might provide sensible approximations.
Comment by Gerónimo — June 14, 2012 @ 5:44 pm |
It is true that once one shows that Neumann heat kernel is increasing toward boundary, the hot-spots conjecture is true. But this approach is much harder than just proving hot-spots conjecture. Until very recently there was Laugesen-Morpurgo conjecture stating the Neumann heat kernel for a ball is increasing toward boundary. This was settled by Pascu and Gageonea (http://www.sciencedirect.com/science/article/pii/S0022123610003526) in 2011 using mirror couplings.
Reflection argument seems very appealing, but even for an interval I have not seen a proof that Neumann heat kernel is increasing using explicit series of Gaussian terms coming from reflections. The above paper also settles interval case. One can also use Dirichlet heat kernel to prove this (http://pages.uoregon.edu/siudeja/neumann.pdf, slides 6 and 7).
For triangles reflections are not enough to cover the plane. You may have to also flip the reflected triangle along the line perpendicular to the reflection side in order to ensure that you can cover the plane. This however means that you loose continuity on the boundary.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 6:07 pm |
A small correction: “diagonal of Neumann heat kernel should be increasing toward boundary”, so should be increasing when x goes to boundary.
should be increasing when x goes to boundary.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 8:32 pm |
It does seem like such a procedure would be hard (perhaps hopelessly so) to implement for triangles that don’t tile the plane nicely (which are most triangles) for the reasons given in the other replies. But if such an argument were to work it would first need to be worked out for the case of an equilateral triangle. I’d be interested in seeing such an argument but I am not sure how it would go…
Suppose the initial heat is a point mass at one corner, and draw out a full tiling of the plane. Then the unreflected heat flow would have a nice Gaussian distribution, and the reflected heat flow could be recovered by folding in all the triangles… but how would you show that the hottest point upon folding is at the corner you started the heat flow at? You have an infinite sum and it is not the case that each triangle in this sum has its maximum at that corner…
Comment by Chris Evans — June 14, 2012 @ 8:26 pm |
A couple of people asked for some pictures of nodal lines.
Here are some on triangles which aren’t isoceles or right or equilateral, and whose angles aren’t within pi/50 of those special cases, either:
Here are the nodal lines corresponding to the 2nd and 3rd Neumann eigenfunction on a nearly equilateral triangle. Note the multiplicity of the 2nd eigenvalue is 1, but the spectral gap \lambda_3-\lambda_2 is small. I found these interesting.
Comment by Nilima Nigam — June 14, 2012 @ 5:16 pm |
Is the nearly equilateral triangle isosceles? If it is, the nearly antisymmetric case should not look the way it does. Every eigenfunction on isosceles triangle must be either symmetric or antisymmetric. Otherwise corresponding eigenvalue is not simple. It is not impossible that the third one is not simple, but for nearly equilateral triangle that is extremely unlikely. Here antisymmetric case is the second eigenvalue, so it must be antisymmetric. Even if this triangle is not isosceles, the change in the shape of the nodal like is really huge.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 3:51 am |
No, the nearly equilateral triangle is not isoceles.
Comment by Nilima Nigam — June 15, 2012 @ 3:54 am |
Also, do you have bounds on how the nodal lines should change as we perturb away from the equilateral triangle in an asymmetric fashion? This would be interesting to compare with.
Comment by Nilima Nigam — June 15, 2012 @ 4:01 am |
No, I do not think I have anything for nodal lines. One of the papers by Antunes and Freitas may have something, but they mostly concentrate on the way eigenvalues change. Nothing for nodal lines. It is quite surprising, and good for us, that the change is so big.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 4:08 am |
In case someone wants to see eigenfunctions of all known triangles and a square (right isosceles triangle), I have written a Mathematica package http://pages.uoregon.edu/siudeja/TrigInt.m. See ?Equilateral and ?Square for usage. A good way to see nodal domains is to use RegionPlot with eigenfunction>0. The package can also be used to facilitated linear deformation for triangles. In particular Transplant moves a function from one triangle to another(put {x,y} as function to see the linear transformation itself). There is a T[a,b] notation for triangle with vertices (0,0) (1,0) and (a,b). Function Rayleigh evaluates Rayleigh quotient of a given function on a given triangles (with one side on x-axis). There are also other helper functions for handling triangles. Everything is symbolic so parameters can be used. Put this in Mathematica to import the package:
AppendTo[$Path,ToFileName[{$HomeDirectory, “subfolder”, “subfolder”}]];
<< TrigInt`
The first line may be needed for Mathematica kernel to see the file. After that
Equilateral[Neumann,Antisymmetric][0,1] gives the first antisymmetric eigenfunction
Equilateral[Eigenvalue][0,1] gives the second eigenvalue
Comment by Anonymous — June 14, 2012 @ 8:15 pm |
There is also a function TrigInt which is much faster than regular Int for complicated trigonometric functions. Limits for the integral can be obtained using Limits[triangle]. For integration it might be a good idea to use extended triangle notation T[a,b,condition] where condition is something like b>0.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 8:20 pm |
I’m not a Mathematica user, so my question may be naive. Are the eigenfunctions being computed symbolically by Mathematica?
If not, could you provide some details on what you’re using to compute the eigenfunctions/values?
It would be great if you could post this information to the Wiki.
Comment by Nilima Nigam — June 15, 2012 @ 4:04 am |
They are computed using general formula. The nicest write-up is probably in the series of papers by McCartin. All eigenfunctions look almost the same, sum of three terms, each is a product of two cosines/sines. The only difference is integer coefficients under trigs. The same formula works for Dirichlet, just a bit different numbers.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 4:12 am |
Here is a code from the package (with small changes for readability). First there are some convenient definitions.
h=1;
r=h/(2Sqrt[3]);
u=r-y;
v=Sqrt[3]/2(x-h/2)+(y-r)/2;
w=Sqrt[3]/2(h/2-x)+(y-r)/2;
Then a function that contains all cases, #1 and #2 are just integers, f and g are trig functions:
EqFun[f_,g_]:=f[Pi (-#1-#2)(u+2r)/(3r)]g[Pi (#1-#2)(v-w)/(9r)]+
f[Pi #1 (u+2r)/(3r)]g[Pi (2#2+#1)(v-w)/(9r)]+
f[Pi #2 (u+2r)/(3r)]g[Pi (-2#1-#2)(v-w)/(9r)];
All the cases:
Equilateral[Neumann,Symmetric]=EqFun[Cos,Cos]&;
Equilateral[Neumann,Antisymmetric]=EqFun[Cos,Sin]&;
Equilateral[Dirichlet,Symmetric]=EqFun[Sin,Cos]&;
Equilateral[Dirichlet,Antisymmetric]=EqFun[Sin,Sin]&;
Eigenvalue is the same regardless of the case. For Neumann you need 0<=#1<=#2. For Dirichlet: 0<#1<=#2. And antisymmetric cannot have #1=#2.
Equilateral[Eigenvalue]=Evaluate[4/27(Pi/r)^2(#1^2+#1 #2+#2^2)]&;
Comment by Bartlomiej Siudeja — June 15, 2012 @ 4:22 am |
I’m sorry, I’m really not familiar with this package. Am I correct, reading the script above, that you are computing an *analytic* expression for the eigenvalue? That is, if I give three angles of an arbitrary triangle(a,b,pi-a-b), your script renders the Neumann eigenvalue and eigenfunction in closed form?
Or is this code for the cases where the closed form expressions for the eigenvalues are known (equilateral, right-angled, etc)? This is also very nice to have, for verification of other methods of calculation.
When we map one triangle to another, the eigenvalue problem changes (see the Wiki, or previous discussions here). It is great if you have a code which can analytically compute the eigenvalues of the mapped operator on a specific triangle, or equivalently, eigenvalues on a generic triangle.
Comment by Nilima Nigam — June 15, 2012 @ 4:36 am |
This package is not fancy at all. It has formulas for equilateral, right isosceles and half of equilateral. These are known explicitly. Fro other triangles it just helps evaluate Rayleigh quotient on something like f composed with T (linear). This just gives upper bounds for eigenvalues. Or it might help speed-up calculations for Hadamard variation, since you do not need to think about what is the linear transformation from one triangle to another. And it can evaluate Rayleigh quotient on transformed triangle Was handy for proving bounds for eigenvalues, and to see nodal domains for known cases.
I wish I had any analytic formula for eigenvalues on arbitrary triangle.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 4:42 am |
OK, thanks for the clarification! I was thrown by your initial comment about it accepting all parameters. Now I understand that you’re able to get good bounds, rather than the exact eigenvalues.
Comment by Nilima Nigam — June 15, 2012 @ 5:23 am |
The fact that there are quite a few known cases means that you can make a linear combination of known eigenfunctions (each transplanted to a given triangle) and evaluate Rayleigh quotient. PDEToolbox is not a benchmark for FEM, but I have seen cases where 16GB of memory was not enough to bring numerical result below upper bound obtained from a test function containing 5 known eigenfunctions.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 5:12 am |
PDEtoolbox is great for generating a quick result, but not for careful numerics, and it doesn’t do high order. Yes, you could wait a long while to get good results if you relied solely on PDEToolBox. Joe Coyle (whose FEM solver we’re using) has implemented high-accuracy conforming approximants, and we’re keeping tight control on residual errors. Details of our approximation strategy are on the Wiki. I’m also thinking of implementing a completely non-variational strategy, so we have two sets of results to compare.
Comment by Nilima Nigam — June 15, 2012 @ 5:29 am |
I used to use PDEToolbox for visualizations, but I no longer have license for it. Besides, it does not have 3D, and eigenvalues in 3D behave much worse than in 2D. I have written a wrapper for eigensolver from FEniCS project (http://fenicsproject.org/). It is most likely not good for rigorous numerics, and I am not even a beginner in FEM. However, it works perfectly for plotting. In particular one can see that nodal line moves away very quickly from vertices. The nearly equilateral case Nilima posted must indeed be extremely close to equilateral. While Nilima crunches the data, anyone who wants to see more pictures is welcome to use my script. It is a rough implementation with no-so-good documentation, but it can handle many domains with any boundary conditions (also mixed). There is a readme file. Download link: http://pages.uoregon.edu/siudeja/fenics.zip. I have not tested this only on Mac, so I am not sure it will work in Windows or Linux, though it should.
To get a triangle one can use
python eig.py tr a b -N -s number -m -c3 -e3
tr is domain specification, a,b is the third vertex, -N gives Neumann, -s number is number of triangles, -m shows mesh, -c3 gives contours instead of surface plots (3 contours are good for nodal line), -e3 to get 3 eigenvalues
There are many options. python eig.py -h lists all of them with minimalistic explanations
Comment by Bartlomiej Siudeja — June 15, 2012 @ 4:57 pm |
Some random thoughts about the nodal line:
1) I believe the Nodal Line Theorem guarantees that the nodal line consists of a curve with end points on the boundary and which divides the triangle into two sub-regions. It might be possible to prove that in fact the two endpoints of the nodal line lie on different sides of the triangle. (The alternate case, that the nodal line looks like a handle sticking out from one of the edges, feels wrong… in fact maybe it is the case that for no domain ever is it the case that the two endpoints of the nodal line lie on the same straight line segment of its boundary).
2) If 1) were true, then it would follow that the nodal line does in fact straddle one of the corners. Moreover, we know apriori that the nodal line is orthogonal to the boundary (so at least locally near the boundary it starts to “bow out”). The nodal line ought not to be too serpentine… that would cause the second eigenfunction to have a large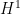 -norm while allowing the
-norm while allowing the 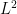 -norm to stay small… which would violate the Raleigh-Ritz formulation of the 2nd eigenfunction.
-norm to stay small… which would violate the Raleigh-Ritz formulation of the 2nd eigenfunction.
3) Since the nodal line is “bowed out” at the boundary, and has incentive not to be serpentine, it seems like it shouldn’t “bow in”. If we could show that the slope/angle of the nodal-line stays within a certain range then the arguments used for the mixed Dirichlet-Neumann triangle could be applied to show that the extremum of the eigenfunction in this sub-region in fact lies at the corner the nodal line is straddling.
Of course this is all hand-wavy and means nothing without precise quantitative estimates :-/
In particular though, does any one know if the statement ” for no domain ever is it the case that the two endpoints of the nodal line lie on the same straight line segment of its boundary” is true? I can’t think of any domain for which that would be the case…
Comment by Chris Evans — June 14, 2012 @ 8:53 pm |
I think your last statement is true. Suppose a nodal line for the Neumann Laplacian in a polygonal domain end both its endpoints on the same line segment. Consider the domain Q enclosed by the nodal line and the piece of the line segment enclosed between the nodal line end-points. This region is a subset of the original domain.
Now, on Q, the eigenfunction u has the following properties: it satisfies in Q, has zero Dirichlet data on the curvy part of the boundary of Q, and satisfies zero Neumann data on the straight line part of its boundary. Now reflect Q across the straight line segment, and you get a Dirichlet problem for
in Q, has zero Dirichlet data on the curvy part of the boundary of Q, and satisfies zero Neumann data on the straight line part of its boundary. Now reflect Q across the straight line segment, and you get a Dirichlet problem for  in the doubled domain.
in the doubled domain.
I now claim cannot be an eigenvalue of the Dirichlet problem on this doubled domain.
cannot be an eigenvalue of the Dirichlet problem on this doubled domain.  is the first eigenvalue of the mixed Dirichlet-Neumann problem on Q. This is easy- there are no other nodal lines in Q. Hence
is the first eigenvalue of the mixed Dirichlet-Neumann problem on Q. This is easy- there are no other nodal lines in Q. Hence  is smaller than the first eigenvalue of the Dirichlet problem on Q (fewer constraints). Doubling the domain just increases the value of the Dirichlet eigenvalue. So
is smaller than the first eigenvalue of the Dirichlet problem on Q (fewer constraints). Doubling the domain just increases the value of the Dirichlet eigenvalue. So  cannot be an eigenvalue on the doubled domain.
cannot be an eigenvalue on the doubled domain.
Finally, we have the Helmholtz problem on the doubled domain, with zero boundary data. We’ve just shown \Lambda is not an eigenvalue, so the problem is uniquely solvable, and hence u=0 in the doubled domain.
on the doubled domain, with zero boundary data. We’ve just shown \Lambda is not an eigenvalue, so the problem is uniquely solvable, and hence u=0 in the doubled domain.
This would be a contradiction.
Comment by Nilima Nigam — June 14, 2012 @ 9:35 pm |
I think there is something wrong with this argument. When you double the domain, the Dirichlet eigenvalue must go down. In fact is exactly equal to the first Dirichlet eigenvalue on doubled Q (which has Dirichlet condition all around). Doubled Q has a line of symmetry, hence by simplicity of the first Dirichlet eigenvalue, the eigenfunction must be symmetric. Hence it must satisfy Neumann condition on the straight part of the boundary of Q.
is exactly equal to the first Dirichlet eigenvalue on doubled Q (which has Dirichlet condition all around). Doubled Q has a line of symmetry, hence by simplicity of the first Dirichlet eigenvalue, the eigenfunction must be symmetric. Hence it must satisfy Neumann condition on the straight part of the boundary of Q.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 10:00 pm |
Yes, of course, you are correct.
Comment by Nilima Nigam — June 14, 2012 @ 11:29 pm |
Once we double the original domain and get a doubled Q with Dirichlet condition all around, we can claim that this domain has larger eigenvalues than the origin domain doubled with Dirichlet all around. Assuming the doubled domain is convex, we can use Payne-Levine-Weinberger inequality , Neumann is below Dirichlet. Without convexity we just have
, Neumann is below Dirichlet. Without convexity we just have  . Our original eigenfunction gives a eigenvalue on the doubled domain, but unfortunately it might not be second. If it was we would be done. Under convexity assumption it should be easier, but I am not sure yet how to finish the proof.
. Our original eigenfunction gives a eigenvalue on the doubled domain, but unfortunately it might not be second. If it was we would be done. Under convexity assumption it should be easier, but I am not sure yet how to finish the proof.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 10:38 pm |
I like the idea of taking advantage of the fact that the boundary is flat to reflect across it, but for the reasons Siudeja mentions I don’t quite follow the argument.
Maybe it is possible to make an argument by reflecting the entire domain (not just the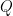 in your notation) across the straight line segment. The reflected eigenfunction would then have a nodal line which is a circle…
in your notation) across the straight line segment. The reflected eigenfunction would then have a nodal line which is a circle…
Thus we would have an eigenfunction which has only *one* nodal line and it is a loop floating in the middle… does the Nodal Line Theorem preclude this?
Comment by Chris Evans — June 14, 2012 @ 11:27 pm |
The unit disk contains a Neumann eigenfunction whose nodal line is a closed circle – but it isn’t the second eigenvalue. But it is the second eigenvalue amongst the radial functions, which already suggests one has to somehow “break the symmetry” (whatever that means) in order to rule out loops…
whose nodal line is a closed circle – but it isn’t the second eigenvalue. But it is the second eigenvalue amongst the radial functions, which already suggests one has to somehow “break the symmetry” (whatever that means) in order to rule out loops…
Comment by Terence Tao — June 15, 2012 @ 12:28 am |
I think that if one can prove that the second eigenfunction of an acute scalene triangle never vanishes at a vertex (i.e. the nodal line cannot cross a vertex), then by a continuity argument (starting from a very thin acute triangle, for instance) shows that for any acute scalene triangle, the nodal line crosses each of the edges adjacent to the pointiest vertex exactly once. I don’t know how to prevent vanishing at a vertex though. (Note that for an equilateral or super-equilateral isosceles triangle, the nodal line does go through the vertex, though as shown in the image http://people.math.sfu.ca/~nigam/polymath-figures/nearly-equilateral-1.jpg from comment 11, the nodal line quickly moves off of the vertex once one perturbs off of the isosceles case.)
I was looking at the argument that shows the nodal line is not a closed loop, hoping to get some mileage out of a reflection argument, but unfortunately it relies on an isoperimetric inequality and does not seem to be helpful here. (The argument is as follows: if the nodal line is a closed loop, enclosing a subdomain D of the original triangle T, then by zeroing out everything outside of the loop we see that the second Neumann eigenvalue of T is at least as large as the first Dirichlet eigenvalue of D, which is in turn larger than the first Dirichlet eigenvalue of T. But there are isoperimetric inequalities that assert that among all domains of a given area, the first Dirichlet eigenvalue is minimised and the second Neumann eigenvalue are maximised at a disk, implying in particular that the Neumann eigenvalue of T is less than or equal to the Dirichlet eigenvalue of T, giving the desired contradiction.)
Comment by Terence Tao — June 14, 2012 @ 10:55 pm |
This is exactly what I was trying to do above. I think that isoperimetric inequality is not needed. Neumann eigenvalue is just equal to Dirichlet in the loop (laplacian is local), which is larger than Dirichlet on the whole domain which is larger than second Neumann on the whole domain (Polya and others). For convex domains even the third Neumann eigenvalue is below the first Dirichlet. But even this is not enough for our case.
Comment by Bartlomiej Siudeja — June 14, 2012 @ 11:04 pm |
I have done a few numerical plots for super-equilateral triangles sheared by very small number. It seems that the speed at which nodal line moves away from the vertex when shearing is growing when isosceles triangle approaches equilateral. For triangle with vertices (0,0), (1,0) and (1/2+epsilon,sqrt(3)/ (2+epsilon)), nodal line looks almost the same regardless of epsilon. I tried epsilon=0.1, 0.01, 0.0001. Nodal line touches the side about 1/3 of the way from vertex.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 6:31 pm |
I think reflection may actually work, unless I am missing something. Let T be the original acute triangle, Q the quadrilateral obtained by reflection, and S the reflection line. We assume that the second Neumann eigenfunction of T has endpoints on S. Now reflect to get interior Dirichlet domain D. This one is smaller than Q, so by domain monotonicity has strictly larger first Dirichlet eigenvalue than Q with Dirichlet boundary conditions. Due to convexity of Q we get that the third Neumann eigenvalue of Q is not larger than the first Dirichlet eigenvalue of Q (http://www.jstor.org/stable/2375044). We will be done if we can show that the second Neumann eigenfunction of T gives the second or third Neumann eigenfunction of Q. Due to line of symmetry in Q, every eigenfunction must be symmetric or antisymmetric. If not, we could reflect it, then add original and reflection to get symmetric. We could also subtract to get antisymmetric. Hence non symmetric eigenfunction of Q implies double eigenvalue. One of those must be symmetric, so it must be the Neumann eigenfunction of T, and we are done. So suppose that the second Neumann eigenfunction on Q is antisymmetric. If the third on is also antisymmetric, it must have additional nodal line, hence by antisymmetry must have at least 4 nodal domains. But this is not possible. Hence either the second or the third eigenfunction on Q must be symmetric, hence it must satisfy Neumann condition on S. Therefore it must be the second eigenfunction on T. Contradiction.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 12:44 am |
Nice! (Though I’m not clear about the line “Non symmetric eigenfunction of Q implies double eigenvalue”, it seems that this is neither true nor needed for the argument. Also, I replaced your jstor link with the stable link.)
Comment by Terence Tao — June 15, 2012 @ 1:20 am |
No symmetry for eigenfunction means that we can reflect the eigenfunction to get a new one (different). Now take a sum to get something symmetric (Neumann on S), subtract to get antisymmetric (DIrichlet on S). Neither one will be 0, and they must be orthogonal. So eigenvalue must be double or higher. This just means that eigenspace for something symmetric can always be decompose into symmetric and antisymmetric.
Comment by Bartlomiej Siudeja — June 15, 2012 @ 1:29 am |
Oh, I see what you mean now. (I had confused “non symmetric” with “anti-symmetric”.) I put a quick writeup of the argument on the wiki.
Comment by Terence Tao — June 15, 2012 @ 1:48 am |
The reference I included was to a paper of Friedlander, where has cites a much older paper by Levine and Weinberger where the inequality is proved. There is also a nice paper by Frank and Laptev that gives good account of who proved what (http://www2.imperial.ac.uk/~alaptev/Papers/FrLap2.pdf).
Comment by Bartlomiej Siudeja — June 15, 2012 @ 2:16 am |
Concerning the method of attack I suggested in the previous comment, it seems that 1) is proven (as the nodal line connects two edges, it does indeed straddle some vertex.
It occurs to me that 2) and 3) can be more succinctly phrased as the conjecture that the mixed boundary domain consisting of this corner and nodal line is *convex*.
I think showing that would be enough… because the nodal line intersects the boundary orthogonally, knowing this region is convex should control the slope of the nodal line enough that earlier arguments would get the extremum in the corner.
Comment by Chris Evans — June 15, 2012 @ 7:27 am |
[…] proposed by Chris Evans, and that has already expanded beyond the proposal post into its first research discussion post. (To prevent clutter and to maintain a certain level or organization, the discussion gets cut up […]
Pingback by Three number theory bits: One elementary, the 3-Goldbach, and the ABC conjecture « mixedmath — June 15, 2012 @ 1:58 pm |
[…] previous research thread for the Polymath7 “Hot Spots Conjecture” project has once again become quite full, so […]
Pingback by Polymath7 research threads 2: the Hot Spots Conjecture « The polymath blog — June 15, 2012 @ 9:49 pm |
As you can see, I’ve rolled over the thread again as this thread is also approaching 100 comments and getting a little hard to follow. The pace is a bit hectic, but I guess this is a good thing, as it is an indication that we are making progress and understanding the problem better…
Comment by Terence Tao — June 15, 2012 @ 9:51 pm |
[…] been quite an active discussion in the last week or so, with almost 200 comments across two threads (and a third thread freshly opened up just now). While the problem is still not completely […]
Pingback by Updates on the two polymath projects « What’s new — June 15, 2012 @ 10:22 pm |
[…] time to roll over the research thread for the Polymath7 “Hot Spots” conjecture, as the previous research thread has again become […]
Pingback by Polymath7 research threads 3: the Hot Spots Conjecture « The polymath blog — June 24, 2012 @ 7:22 pm |
Such an insightful read! Your blog consistently delivers valuable content that keeps me engaged and enlightened. Thank you for sharing your knowledge and expertise with us. <a href=”https://adyanthwealth.in/portfolio-management-service/“> Best Portfolio Management Services </a>
Comment by Anonymous — May 22, 2024 @ 10:17 am |