The polymath blog

June 3, 2012

Polymath proposal: The Hot Spots Conjecture for Acute Triangles

Filed under: hot spots,polymath proposals — Terence Tao @ 2:59 am

Chris Evans has proposed a new polymath project, namely to attack the “Hot Spots conjecture” for acute-angled triangles.   The details and motivation of this project can be found at the above link, but this blog post can serve as a place to discuss the problem (and, if the discussion takes off, to start organising a more formal polymath project around it).

November 13, 2011

Lipton’s Polymath Proposal: The Group Isomorphism Problem

Filed under: polymath proposals — Gil Kalai @ 10:16 am
Tags: , ,

Dick Lipton proposes the group isomorphism problem as a new polymath project.

May 12, 2011

Possible new polymath project

Filed under: polymath proposals — Terence Tao @ 5:56 pm

Richard Lipton has just proposed on his blog to discuss the following conjecture of Erdos as a polymath project: that there are no natural number solutions to the equation

1^k + \ldots + (m-1)^k = m^k

with k \geq 2.  Previous progress on this problem (including, in particular, a proof that any solution to this equation must have an extremely large value of m, and specifically that m \geq 10^{10^9}) can be found here.

February 5, 2011

Polymath6: improving the bounds for Roth’s theorem

Filed under: polymath proposals — gowers @ 12:03 pm

For the time being this is an almost empty post, the main purpose of which is to provide a space for mathematical comments connected with the project of assessing whether it is possible to use the recent ideas of Sanders and of Bateman and Katz to break the 1/\log N barrier in Roth’s theorem. (In a few hours’ time I plan to write a brief explanation of what one of the main difficulties seems to be.)

Added later. Tom Sanders made the following remarks as a comment. It seems to me to make more sense to have them as a post, since they are a good starting point for a discussion. So I have taken the liberty of upgrading the comment. Thus, the remainder of this post is written by Tom.

This will hopefully be an informal post on one aspect of what we might need to do to translate the Bateman-Katz work into the \mathbb{Z}/N\mathbb{Z} setting.

One of the first steps in the Bateman-Katz argument is to note that if A \subset \mathbb{F}_3^n is a cap-set (meaning it is free of three-term progressions) of density \alpha then we can assume that there are no large Fourier coefficients, meaning

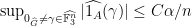\sup_{0_{\widehat{G}}\neq\gamma \in \widehat{\mathbb{F}_3^n}}{|\widehat{1_A}(\gamma)|} \leq C\alpha/n.

They use this to develop structural information about the large spectrum, 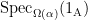\rm{Spec}_{\Omega(\alpha)}(1_A), which consequently has size between \Omega(C^{-3}n^3) and O(\alpha^{-3}). This structural information is then carefully analysed in the `beef’ of the paper. (more…)

July 8, 2010

Minipolymath2 project: IMO 2010 Q5

Filed under: polymath proposals — Terence Tao @ 3:56 pm

This post marks the official opening of the mini-polymath2 project to solve a problem from the 2010 IMO.  I have selected the fifth question (which appears to be slightly more challenging than the sixth, for a change) as the problem to focus on:

Problem. In each of six boxes B_1, B_2, B_3, B_4, B_5, B_6 there is initially one coin. There are two types of operation allowed:
  1. Type 1: Choose a nonempty box B_j with 1 \leq j \leq 5. Remove one coin from B_j and add two coins to B_{j+1}.
  2. Type 2: Choose a nonempty box B_k with 1 \leq k \leq 4. Remove one coin from B_k and exchange the contents of (possibly empty) boxes B_{k+1} and B_{k+2}.
Determine whether there is a finite sequence of such operations that results in boxes B_1, B_2, B_3, B_4, B_5  being empty and box B_6 containing exactly 2010^{2010^{2010}} coins. (Note that a^{b^c} := a^{(b^c)}.)
The comments to this post shall serve as the research thread for the project, in which participants are encouraged to post their thoughts and comments on the problem, even if (or especially if) they are only partially conclusive.  Participants are also encouraged to visit the discussion thread for this project, and also to visit and work on the wiki page to organise the progress made so far.
This project will follow the general polymath rules.  In particular:
  1. All are welcome. Everyone (regardless of mathematical level) is welcome to participate.  Even very simple or “obvious” comments, or comments that help clarify a previous observation, can be valuable.
  2. No spoilers! It is inevitable that solutions to this problem will become available on the internet very shortly.  If you are intending to participate in this project, I ask that you refrain from looking up these solutions, and that those of you have already seen a solution to the problem refrain from giving out spoilers, until at least one solution has already been obtained organically from the project.
  3. Not a race. This is not intended to be a race between individuals; the purpose of the polymath experiment is to solve problems collaboratively rather than individually, by proceeding via a multitude of small observations and steps shared between all participants.   If you find yourself tempted to work out the entire problem by yourself in isolation, I would request that you refrain from revealing any solutions you obtain in this manner until after the main project has reached at least one solution on its own.
  4. Update the wiki. Once the number of comments here becomes too large to easily digest at once, participants are encouraged to work on the wiki page to summarise the progress made so far, to help others get up to speed on the status of the project.
  5. Metacomments go in the discussion thread. Any non-research discussions regarding the project (e.g. organisational suggestions, or commentary on the current progress) should be made at the discussion thread.
  6. Be polite and constructive, and make your comments as easy to understand as possible. Bear in mind that the mathematical level and background of participants may vary widely.

Have fun!

June 12, 2010

Mini-polymath proposal: IMO 2010 Q6

Filed under: news,planning,polymath proposals — Terence Tao @ 11:16 pm

I am proposing the sixth question for the 2010 International Mathematical Olympiad (traditionally, the trickiest of the six problems) as a mini-polymath project for next month.  Details and discussions are in this post on my other blog.

[Update, June 27: the project is scheduled to start on Thursday, July 8 16:00 UTC.]


January 9, 2010

Polymath5: Erdős’s discrepancy problem

Filed under: polymath proposals — Gil Kalai @ 10:56 pm

Is taking place on Gowers’s blog!

December 31, 2009

Proposal (Tim Gowers): Erdos’ Discrepancy Problem

Filed under: polymath proposals — Gil Kalai @ 3:11 pm

For a description of Erdos’ discrepancy problem and a large discussion see this blog on Gowers’s blog.

The decision for the next polymath project over Gowers’s blog will be between three projects: The polynomial DHJ problem, Littlewood problem, and the Erdos discrepency problem. To help making the decision four polls are in place!

November 20, 2009

Proposals (Tim Gowers): Polynomial DHJ, and Littlewood’s problem

Filed under: polymath proposals — Gil Kalai @ 10:06 am

Tim Gowers described two additional proposed polymath projects. One about the first unknown cases of the polynomial Density Hales Jewett problem. Another about the Littelwood’s conjecture.

I will state one problem from each of these posts:

1) (Related to polynomial DHJ) Suppose you have a family \cal F of graphs on n labelled vertices, so that we do not two graphs in the family G,H such that H is a subgraph of G and the edges of G which are not in H form a clique. (A complete graph on 2 or more vertices.) can we conclude that |{\cal F}| =2^{o({{n} \choose {2}}}? (In other words, can we conclude that \cal F contains only a diminishing fraction of all graphs?)

Define the “distance” between two points in the unit cube as the product of the absolute value of the differences in the three coordinates. (See Tim’s remark below.)

2) (Related to Littlewood) Is it possible to find n points in the unit cube [0,1]^3 so that the “distance” between any two of them is at least 1/100000000000000000000n?

A negative answer to Littlewood’s problem will imply a positive answer to problem 2 (with some constant). So the pessimistic saddle thought would be that the answer to Problem 2 is yes without any bearing on Littlewood’s problem.

November 8, 2009

Proposal (Tim Gowers) The Origin of Life

Filed under: polymath proposals — Gil Kalai @ 12:54 pm

Early Earth

 

 

 

 

 

 

 

 

 

A presentation of one possible near future polymath: the mathematics of the origin of life can be found on Gowers’s blog.

« Previous Page — Next Page »

Blog at WordPress.com.