This thread marks the formal launch of “Finding primes” as the massively collaborative research project Polymath4, and now supersedes the proposal thread for this project as the official “research” thread for this project, which has now become rather lengthy. (Simultaneously with this research thread, we also have the discussion thread to oversee the research thread and to provide a forum for casual participants, and also the wiki page to store all the settled knowledge and accumulated insights gained from the project to date.) See also this list of general polymath rules.
The basic problem we are studying here can be stated in a number of equivalent forms:
Problem 1. (Finding primes) Find a deterministic algorithm which, when given an integer k, is guaranteed to locate a prime of at least k digits in length in as quick a time as possible (ideally, in time polynomial in k, i.e. after
steps).
Problem 2. (Finding primes, alternate version) Find a deterministic algorithm which, after running for k steps, is guaranteed to locate as large a prime as possible (ideally, with a polynomial number of digits, i.e. at least
digits for some
.)
To make the problem easier, we will assume the existence of a primality oracle, which can test whether any given number is prime in O(1) time, as well as a factoring oracle, which will provide all the factors of a given number in O(1) time. (Note that the latter supersedes the former.) The primality oracle can be provided essentially for free, due to polynomial-time deterministic primality algorithms such as the AKS primality test; the factoring oracle is somewhat more expensive (there are deterministic factoring algorithms, such as the quadratic sieve, which are suspected to be subexponential in running time, but no polynomial-time algorithm is known), but seems to simplify the problem substantially.
The problem comes in at least three forms: a strong form, a weak form, and a very weak form.
- Strong form: Deterministically find a prime of at least k digits in poly(k) time.
- Weak form: Deterministically find a prime of at least k digits in
time, or equivalently find a prime larger than
in time O(k) for any fixed constant C.
- Very weak form: Deterministically find a prime of at least k digits in significantly less than
time, or equivalently find a prime significantly larger than
in time O(k).
The pr0blem in all of these forms remain open, even assuming a factoring oracle and strong number-theoretic hypotheses such as GRH. One of the main difficulties is that we are seeking a deterministic guarantee that the algorithm works in all cases, which is very different from a heuristic argument that the algorithm “should” work in “most” cases. (Note that there are already several efficient probabilistic or heuristic prime generation algorithms in the literature, e.g. this one, which already suffice for all practical purposes; the question here is purely theoretical.) In other words, rather than working in some sort of “average-case” environment where probabilistic heuristics are expected to be valid, one should instead imagine a “Murphy’s law” or “worst-case” scenario in which the primes are situated in a “maximally unfriendly” manner. The trick is to ensure that the algorithm remains efficient and successful even in the worst-case scenario.
Below the fold, we will give some partial results, and some promising avenues of attack to explore. Anyone is welcome to comment on these strategies, and to propose new ones. (If you want to participate in a more “casual” manner, you can ask questions on the discussion thread for this project.)
Also, if anything from the previous thread that you feel is relevant has been missed in the text below, please feel free to recall it in the comments to this thread.
— Partial results —
One way to proceed is to find a sparse explicitly enumerable set of large integers which is guaranteed to contain a prime. One can then query each element of that set in turn using the primality oracle to then find a large prime.
For instance, Bertrand’s postulate shows that there is at least one prime of k digits in length, which can then be located in time. A result of Baker and Harman shows that there is a prime between n and
for all sufficiently large n, so by using the interval
one can find a k-digit prime in
time. This is currently the best result known unconditionally. Assuming the Riemann hypothesis, there is a prime between n and
, giving the slight improvement to
. (Assuming GRH, it seems that one may be able to improve this a little bit using the W-trick, but this has not been checked.) There is a conjecture of Cramer that the largest prime gap between primes of size n is
which would give a substantial improvement, to
, thus solving the strong form of the conjecture, but we have no idea how to establish this conjecture though it is heuristically plausible.
In a slightly different direction, there is a result of Friedlander and Iwaniec that there are infinitely many primes of the form , and in fact their argument shows that there is a k-digit prime of this form for all large k. This gives a run time of
. A subsequent result of Heath-Brown achieves a similar result for primes of the form
, which gives a slightly better run time of
, but this is still inferior to the Baker-Harman bound.
Strategy 1: Find some even sparser sets than these for which we actually have a chance of proving that the set captures infinitely many primes.
(For instance, assuming a sufficiently quantitative version of Schinzel’s hypothesis H, one would be able to answer the weak form of the problem, though this hypothesis is far from being resolved in general. More generally, there are many sparse sets which heuristically have an extremely good chance of capturing a lot of primes, but the trick is to find a set for which we can provably establish the existence of primes.)
Another approach is based on variants of Euclid’s proof of the infinitude of primes and rely on the factoring oracle. For instance, one can generate an infinite sequence of primes recursively by setting each
to be the largest prime factor of
(here we use the factoring oracle). After k steps, this is guaranteed to generate a prime which is as large as the
prime, which is about
by the prime number theorem. (In general, it is likely that one would find much larger primes than this, but remember that we are trying to control the worst-case scenario, not the average-case one.)
Strategy 2. Adapt the Euclid-style algorithms to get larger primes than this in the worst-case scenario.
For comparison, note that the Riemann hypothesis argument given above would give a prime of size about or more in k steps.
A third strategy is to look for numbers that are not S-smooth for some threshold S, i.e. contain at least one prime factor larger than S. Factoring such a number will clearly generate a prime larger than S. (Furthermore, if the non-S-smooth number is of size less than , it must in fact be prime.) One strategy is to scan an interval [n, n+a] for non-smooth numbers, thus leading to
Problem 3. For which n, a, S can we rigorously show that [n,n+a] contains at least one non-S-smooth number?
If we can make S much larger than a, then we are in business (e.g. if we can make S larger than , then we will beat the RH bound). Unfortunately, if S is larger than a, we know that [0,a] does not contain any non-S-smooth number, which makes it difficult to see how to show that [n,n+a] will contain any non-S-smooth numbers, since sieve theory techniques are generally insensitive to the starting point of an interval.
One interesting proposal to do this, raised by Tim Gowers, is to try to use additive combinatorics. Let J be a set of primes larger than S (e.g. the primes between S and 2S), and let K be the set of logarithms of J. If we can show that one of the iterated sumsets intersects the interval
, then we have shown that [n,n+a] contains at least one non-S-smooth number. The hope is that additive combinatorial methods can provide some dispersal and mixing properties of these iterated sumsets which will exclude a “Murphy’s law” type scenario in which the interval
is always avoided.
Strategy 3. Find good values of n, a, S for which the above argument has a reasonable chance of working.
A fourth strategy would be to try to generate pseudoprimes rather than primes, e.g. to generate numbers obeying congruences such as . It is not clear though how to efficiently achieve this, especially in the worst-case scenario.
A fifth strategy would be to try to understand the following question:
Problem 4. Given a set A of numbers, what is an efficient way to deterministically find a k-digit number which is not divisible by any element of A?
Note that Problem 1 is basically the special case of Problem 4 when A is equal to all the natural numbers (or primes) less than .
A last minute addition to the above strategies, suggested by Ernie Croot:
Strategy 6. Assume the existence of a Siegel zero at some modulus M, which implies that the Jacobi symbol
is equal to -1 for all small primes (say
). Can one use this sort of information to locate a large prime, perhaps by using the quadratic form
? Note that M might not be known in advance. This could lead to a non-trivial disjunction: either we can solve the primes problem, or we can assume that there are no Siegel zeroes in a certain range.
There may be additional viable strategies beyond the above ones. Please feel free to share your thoughts, but remember that we will eventually need a rigorous worst-case analysis for any proposed strategy; heuristics are not sufficient by themselves to resolve the problem.
— Other variants —
There are some variants of the problem that have already been solved, for instance finding irreducible polynomials of a certain degree over a finite field is easy, as is finding square-free numbers of a certain size. It may be worth looking for additional variant problems which are easier but are not yet solved.
We have an argument that shows that in the presence of some oracles, and replacing primes by a similarly dense set of “pseudoprimes”, the problem cannot be solved. It may be of interest to refine this argument to show that even if one assumes complexity-theoretic conjectures such as P=BPP, the general problem of finding pseudoprimes is not efficiently solvable. (We know that the problem is solvable though if P=NP.)
The following toy problem has been advanced:
Problem 5. (Finding consecutive square-free numbers) Find a deterministic algorithm which, when given an integer k, is guaranteed to locate a pair n,n+1 of consecutive square-free numbers of at least k digits in length in as quick a time as possible.
Note that finding one large square-free number is easy: just multiply lots of distinct small primes together. Also, as the density of square-free numbers is , a counting argument shows that pairs of consecutive square-free numbers exist in abundance, and are thus easy to find probabilistically. Testing a number for square-freeness is trivial with a factoring oracle. (Question: is there a deterministic polynomial-time algorithm to test a k-digit number for square-freeness without assuming any oracles?)
For Question 6, it has been suggested that Sylvester’s sequence may be a good candidate; interestingly, this sequence has also been proposed for Strategy 2.
[…] primes” has now officially launched at the polymath blog as Polymath4, with the opening of a fresh research thread to discuss the following problem: Problem 1. Find a deterministic algorithm which, when given an […]
Pingback by Polymath4 (”Finding Primes”) now officially active « What’s new — August 9, 2009 @ 4:08 am |
While scanning through the literature on Sylvester’s sequence, I found the following theorem of Odoni: The number of primes less than that divide some Sylvester number is
that divide some Sylvester number is 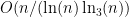 , where
, where  denotes a triple iterated logarithm. This should give a (very) slight improvement to strategy 2, namely we should be guaranteed to find a prime of size
denotes a triple iterated logarithm. This should give a (very) slight improvement to strategy 2, namely we should be guaranteed to find a prime of size 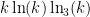 in
in  steps. Of course, this is still far from our best method. Odoni’s paper is: On the prime divisors of the sequence wn+1 = 1+ w1 · · ·wn. J. London Math. Soc. (2), 32(1):1–11, 1985.
steps. Of course, this is still far from our best method. Odoni’s paper is: On the prime divisors of the sequence wn+1 = 1+ w1 · · ·wn. J. London Math. Soc. (2), 32(1):1–11, 1985.
Comment by Mark Lewko — August 9, 2009 @ 4:20 am |
That’s interesting… it suggests a new strategy:
Strategy 7: Find an explicit sequence of mutually coprime numbers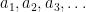 , such that the number of primes less than n that divide any element of the sequence is significantly less than
, such that the number of primes less than n that divide any element of the sequence is significantly less than  .
.
If, for instance, only primes less than n divide an element of the sequence, then we can find a prime of size about
primes less than n divide an element of the sequence, then we can find a prime of size about 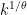 by factoring
by factoring  . Having
. Having  less than 0.535 would beat our current unconditional world record, but any
less than 0.535 would beat our current unconditional world record, but any  would be interesting, I think.
would be interesting, I think.
Comment by Terence Tao — August 9, 2009 @ 4:33 am |
Here’s a thought. Any square-free number which is the sum of two squares can’t have any prime factor equal to 3 mod 4, which already knocks out half the primes from contention.
More generally, if a square-free number is of the form , then it can’t have any prime factor with respect to which -k is not a square. So, if one can find a square-free number that has many representations of the form
, then it can’t have any prime factor with respect to which -k is not a square. So, if one can find a square-free number that has many representations of the form  for various values of k, its prime factors have to avoid a large number of residue classes (by quadratic reciprocity) and are thus forced to lie in a sparse set. If one can then find many coprime numbers of this form, one may begin to find large prime factors, following Strategy 7.
for various values of k, its prime factors have to avoid a large number of residue classes (by quadratic reciprocity) and are thus forced to lie in a sparse set. If one can then find many coprime numbers of this form, one may begin to find large prime factors, following Strategy 7.
Admittedly, we’re already struggling to generate square-free numbers with extra properties, but suppose we ignore that issue for the moment – is it easy to generate numbers which are simultaneously representable by a large number of quadratic forms?
Comment by Terence Tao — August 9, 2009 @ 5:26 am |
I’m not sure what you mean – any number has that form for any
has that form for any  , with
, with  . There are other
. There are other  whenever
whenever 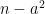 has a square factor.
has a square factor.
This reminds me of OEIS sequence A074885, of numbers for which all positive numbers
for which all positive numbers 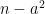 are square-free. There seem to be exactly 436 of these numbers.
are square-free. There seem to be exactly 436 of these numbers.
Comment by Michael Peake — August 9, 2009 @ 12:48 pm |
Oh, I was thinking of keeping k fixed and small.
For instance, given an integer n of the form a^2+3b^2, quadratic reciprocity tells us that every prime factor of n (other than 3) that doesn’t divide it twice is equal to 1 mod 3. (In particular, if n is square-free, every prime factor is of this form).
Thus, if we can find n which is of the form a^2+3b^2 and also of the form c^2+d^2, and is square-free, larger than 6, then it has a prime factor which is both 1 mod 4 and 1 mod 3, i.e. 1 mod 12. So if one can generate a lot of coprime numbers of this form and factor them, one generates primes in a mildly sparse sequence (1/4 of all primes). If one could keep doing this with more and more quadratic forms then one starts getting a reasonably sparse sequence of primes…
Comment by Terence Tao — August 9, 2009 @ 2:33 pm |
It seems like the easiest “polynomial” way to do this is to take integer values of the cyclotomic polynomials, e.g. integer values of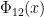 have only prime factors dividing
have only prime factors dividing  or congruent to
or congruent to 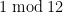 . Formulas (32) and (33) on the Mathworld article make it possible to recursively compute, say,
. Formulas (32) and (33) on the Mathworld article make it possible to recursively compute, say,  for
for  the product of the first
the product of the first  primes given
primes given  .
.
Unfortunately, this runs into the same problem of feeding double-exponential numbers into the factoring oracle mentioned below, since the Fermat numbers are just . To make this feasible one would have to be able to get a lot of information by taking many integer values of a cyclotomic polynomial of reasonably small degree. Alternately one could homogenize into a polynomial of two variables, mimicking the quadratic form case, and take many small coprime values of the variables. I don’t know if there’s a good theory of simultaneous representation by quadratic forms in the literature, but then again I’m not really a number-theorist.
. To make this feasible one would have to be able to get a lot of information by taking many integer values of a cyclotomic polynomial of reasonably small degree. Alternately one could homogenize into a polynomial of two variables, mimicking the quadratic form case, and take many small coprime values of the variables. I don’t know if there’s a good theory of simultaneous representation by quadratic forms in the literature, but then again I’m not really a number-theorist.
Comment by Qiaochu Yuan — August 9, 2009 @ 4:19 pm |
Are the cyclotomic polynomials (say, ) efficiently computable (i.e., polynomial-time in the length of k) in general? The advantage of the Fermat numbers, at least, is that one can use repeated squaring to cut the number of multiplications down to k (and if there is a way to get around the double-exponential problem, this’ll likely be at its heart), but in general
) efficiently computable (i.e., polynomial-time in the length of k) in general? The advantage of the Fermat numbers, at least, is that one can use repeated squaring to cut the number of multiplications down to k (and if there is a way to get around the double-exponential problem, this’ll likely be at its heart), but in general  has as many as
has as many as  terms, and is irreducible, so repeated squaring doesn’t obviously apply.
terms, and is irreducible, so repeated squaring doesn’t obviously apply.
Comment by Harrison — August 9, 2009 @ 4:44 pm |
Formulas (32) and (33) take the place of repeated squaring, but the number of factors in the final product is the number of prime factors of . I think one still gets an essentially polynomial-time computation though, especially as the computations involved in many of the factors can be recycled. (This is all assuming we used the W-trick or some variant thereof, so we know the factorization of
. I think one still gets an essentially polynomial-time computation though, especially as the computations involved in many of the factors can be recycled. (This is all assuming we used the W-trick or some variant thereof, so we know the factorization of  .)
.)
So combining some observations it may or may not be a good idea to compute something like (the homogeneous version). Unfortunately this is still essentially double-exponential as far as I can tell.
(the homogeneous version). Unfortunately this is still essentially double-exponential as far as I can tell.
Comment by Qiaochu Yuan — August 9, 2009 @ 6:40 pm |
I don’t think we quite have , but it's known that the prime divisors of Fermat numbers
, but it's known that the prime divisors of Fermat numbers 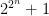 are fairly sparse, since the sum of their reciprocals converges.
are fairly sparse, since the sum of their reciprocals converges.
But actually we don’t even need that result — it’s a very, very old theorem of Euler that all the prime factors of the nth Fermat number are at least exponential in n! (In particular, they have the form .) The problem, of course, is again that Fermat numbers are exponentially long, and it doesn’t seem possible to get around the double-exponential bind. (Although I’d be thrilled to be wrong about that!)
.) The problem, of course, is again that Fermat numbers are exponentially long, and it doesn’t seem possible to get around the double-exponential bind. (Although I’d be thrilled to be wrong about that!)
Comment by Harrison — August 9, 2009 @ 3:30 pm |
The Křížek, Luca and Somer result (On the convergence of series of reciprocals of primes related to the Fermat numbers, J. Number Theory 97(2002), 95–112) actually establishes that the set of primes less than that divide some Fermat number is
that divide some Fermat number is 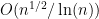 . Moreover, Fermat’s numbers are known to be coprime. Shouldn’t this give strategy 7 with
. Moreover, Fermat’s numbers are known to be coprime. Shouldn’t this give strategy 7 with  near
near  ?
?
Comment by Mark Lewko — August 9, 2009 @ 6:21 pm |
Well, yes and no, as I understand it. We do have an explicit sequence whose set of prime factors is very sparse, and so we can indeed find a prime of size about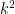 by factoring the first k Fermat numbers. But the sequence grows so fast that the rate-determining step, as it is, isn’t factoring the integers but just writing them down! So computing these factors actually takes way more than k steps. (I could be wrong, though, since I’m a bit fuzzy on what exactly constitutes a “step.”)
by factoring the first k Fermat numbers. But the sequence grows so fast that the rate-determining step, as it is, isn’t factoring the integers but just writing them down! So computing these factors actually takes way more than k steps. (I could be wrong, though, since I’m a bit fuzzy on what exactly constitutes a “step.”)
Still, it’s an interesting result, and I’d be interested in seeing their proof method.
Comment by Harrison — August 9, 2009 @ 7:10 pm |
There at at least two other places in the thread I could put this comment, but here goes:
One can get an improvement in the base of the double logarithm by considering the homogeneous polynomial and then taking
and then taking 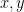 to be conjugate algebraic integers of small absolute value. The obvious choice is to take
to be conjugate algebraic integers of small absolute value. The obvious choice is to take 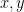 to be the golden ratios, which gives the Lucas numbers
to be the golden ratios, which gives the Lucas numbers  . These can be computed roughly as efficiently as the Fermat numbers thanks to the recurrence
. These can be computed roughly as efficiently as the Fermat numbers thanks to the recurrence  for
for  and they have similar divisibility properties to the Fermat numbers, but grow more slowly. (Still double-exponential, of course.) More precisely, any prime factor of
and they have similar divisibility properties to the Fermat numbers, but grow more slowly. (Still double-exponential, of course.) More precisely, any prime factor of  is congruent to
is congruent to 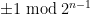 .
.
This opens up the possibility of looking at other algebraic integers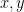 , which corresponds to looking at other sequences satisfying two-term linear recurrences or, if you’re Richard Lipton, taking traces of
, which corresponds to looking at other sequences satisfying two-term linear recurrences or, if you’re Richard Lipton, taking traces of 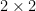 matrices with integer entries. As I mentioned on his post, the Mahler measure problem and other problems related to finding algebraic integers with all conjugates small in absolute value seem to be relevant here. (Lipton’s ideas about factoring could also be relevant in other ways to this problem.)
matrices with integer entries. As I mentioned on his post, the Mahler measure problem and other problems related to finding algebraic integers with all conjugates small in absolute value seem to be relevant here. (Lipton’s ideas about factoring could also be relevant in other ways to this problem.)
Of course these remarks extend to other cyclotomic polynomials as well.
What happens when you plug conjugate algebraic integers into a quadratic form?
Comment by Qiaochu Yuan — August 9, 2009 @ 6:24 pm |
Euclid’s argument is really that if $ latex p_1,…,p_n$ are primes, then none of them can divide . This can be generalized to none of them can divide
. This can be generalized to none of them can divide
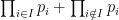 , for any subsect
, for any subsect
 . By considering prime divisor, similar argument shows that if
. By considering prime divisor, similar argument shows that if 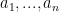 are pairwise coprime, then
are pairwise coprime, then
 is prime to all of them. One can also
is prime to all of them. One can also and sign
and sign  (which may be chosen randomly) and let
(which may be chosen randomly) and let
 .
. eg
eg  , one has many ways to extend to an infinite sequence of coprime integers (each giving a proof that there are infinitely many primes). Staring with primes, one can also take smallest prime divisor of
, one has many ways to extend to an infinite sequence of coprime integers (each giving a proof that there are infinitely many primes). Staring with primes, one can also take smallest prime divisor of  to get a sequence of distinct primes. To minimize growth, I guess one example is to pick
to get a sequence of distinct primes. To minimize growth, I guess one example is to pick 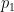 to be any prime and let
to be any prime and let
 to be the smallest prime minimized over all prime divisors of
to be the smallest prime minimized over all prime divisors of
 , minimized over all subsets
, minimized over all subsets  , over all signs, and over a bounded set of powers
, over all signs, and over a bounded set of powers  say. I am not sure how small one can bound the growth in this case.
say. I am not sure how small one can bound the growth in this case.
add arbitrary positive powers
So starting with any set of coprime integers
Comment by KokSeng Chua — August 11, 2009 @ 1:07 pm |
Actually, if the Sylvester sequence is square-free, then there must be an exponentially large prime factor of the k^th element a_k, because a_k is double-exponentially large in k, and it is the product of distinct primes if it is square free; it is an elementary result that the product of the first n primes is exponentially growing in n, so the largest prime factor of a_k has to be at least exponentially large.
On the other hand, one is feeding in a double-exponentially large number into the factoring oracle, which is sort of cheating; it would take an exponential amount of time just to enter in the digits of this number (unless one defined it implicitly, for instance as the output of an arithmetic circuit). Even if factoring was available in polynomial time, it would still take exponential time to factor the k^th Sylvester number. The problem is that the sequence grows far too quickly…
Comment by Terence Tao — August 9, 2009 @ 2:27 pm |
We can even do better than the Sylvester sequence, since it’s a result of Euler that the prime factors of the nth Fermat number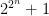 all have the form
all have the form  , so unconditionally we can find an exponentially large prime by factoring
, so unconditionally we can find an exponentially large prime by factoring 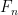 . But of course this sequence is also double-exponential, which I’d argue isn’t just “sort of cheating,” it is cheating! I don’t think it’s possible to escape the double-exponential bind, and as you point out, even if it were, we’d still be cheating by assuming factoring in constant time, which is only a reasonable simplification when we’re factoring polynomially-large numbers.
. But of course this sequence is also double-exponential, which I’d argue isn’t just “sort of cheating,” it is cheating! I don’t think it’s possible to escape the double-exponential bind, and as you point out, even if it were, we’d still be cheating by assuming factoring in constant time, which is only a reasonable simplification when we’re factoring polynomially-large numbers.
Can we find an explicit sequence that’s exponential in some subexponential function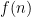 which is guaranteed to have large prime factors? I can’t think of a candidate, but maybe someone cleverer can.
which is guaranteed to have large prime factors? I can’t think of a candidate, but maybe someone cleverer can.
Sorry if this double-posts; something happened to the first comment of this nature I wrote and it’s not showing up.
Comment by Harrison — August 9, 2009 @ 3:41 pm |
A slighly
Comment by Joel — August 9, 2009 @ 4:10 pm |
Sorry about my last (not)comment. I can’t erase it.
A slightly improve to that would be to use the cyclotomic polynomials, since every prime which divides but not
but not  must be congruent with 1 modulo
must be congruent with 1 modulo  . Making
. Making  , as the degree of
, as the degree of 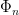 is
is 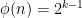 , we have that any prime divisor of
, we have that any prime divisor of 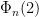 (which is odd and about
(which is odd and about 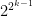 ) is bigger than
) is bigger than 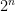 .
.
Comment by Joel Moreira — August 9, 2009 @ 4:30 pm |
See my comment above. In order for the other cyclotomic polynomials to really be practical one would have to be able to get the ratio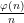 to decrease quickly, and there’s no good way to do this other than to take
to decrease quickly, and there’s no good way to do this other than to take  to be the product of the first few primes; even then the gain is too minuscule and we’re still essentially dealing with double-exponential numbers.
to be the product of the first few primes; even then the gain is too minuscule and we’re still essentially dealing with double-exponential numbers.
Comment by Qiaochu Yuan — August 9, 2009 @ 4:35 pm |
And just so it’s clear for anyone else reading, is precisely the Fermat number
is precisely the Fermat number 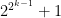 , and the
, and the 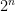 at the end of Joel’s comment should be
at the end of Joel’s comment should be  ; that is, the result Harrison cited is actually slightly stronger than the cyclotomic result.
; that is, the result Harrison cited is actually slightly stronger than the cyclotomic result.
Comment by Qiaochu Yuan — August 9, 2009 @ 4:46 pm |
Well, using Euler’s result that all prime factors of Fermat numbers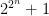 are at least
are at least  , we at least have the ability to obtain a prime of size
, we at least have the ability to obtain a prime of size  by factoring a single k-digit number, which is comparable to what we can do from trivial methods. So any improvement on this would be somewhat nontrivial, I think.
by factoring a single k-digit number, which is comparable to what we can do from trivial methods. So any improvement on this would be somewhat nontrivial, I think.
Comment by Terence Tao — August 9, 2009 @ 6:05 pm |
I’d like to start the ball rolling with a preliminary analysis of Tim Gowers’ approach (Strategy 3).
Suppose we want to find a prime larger than some given large threshold S, assuming a factoring oracle. Right now, Bertrand’s postulate gives us an O(S) algorithm, and more fancy results in number theory give us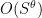 for various values of
for various values of  (3/4, 2/3, 0.535, 1/2). I think to begin with, we would be happy if the additive combinatorics approach could give an
(3/4, 2/3, 0.535, 1/2). I think to begin with, we would be happy if the additive combinatorics approach could give an 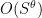 algorithm for some
algorithm for some  , even if it doesn't beat the strongest number-theoretic based algorithm for now.
, even if it doesn't beat the strongest number-theoretic based algorithm for now.
Let K be the logarithms of the primes between S and 2S. Thus this set consists of about numbers in the interval
numbers in the interval ![[\log S, \log S+\log 2]](https://s0.wp.com/latex.php?latex=%5B%5Clog+S%2C+%5Clog+S%2B%5Clog+2%5D&bg=ffffff&fg=000000&s=0&c=20201002) . It's quite uniformly distributed in a Fourier sense (especially if one assumes the Riemann hypothesis).
. It's quite uniformly distributed in a Fourier sense (especially if one assumes the Riemann hypothesis).
Experience has shown that double sumsets K+K tend to be well behaved almost everywhere, but triple sumsets K+K+K and higher are well behaved everywhere. (Thus, for instance, the odd Goldbach conjecture is solved for all large odd numbers, but the even Goldbach conjecture is only known for ''almost'' all large even numbers, even assuming GRH.) So it seems reasonable to look at the triple sumset K+K+K, which is lying in the interval![[3 \log S, 3 \log S + 3 \log 2]](https://s0.wp.com/latex.php?latex=%5B3+%5Clog+S%2C+3+%5Clog+S+%2B+3+%5Clog+2%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Suppose we are looking to find a non-S-smooth number in time (say). It would suffice to show that the interval
(say). It would suffice to show that the interval ![[T, T + S^{-2.01}]](https://s0.wp.com/latex.php?latex=%5BT%2C+T+%2B+S%5E%7B-2.01%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) contains an element of K+K+K for some fixed T in
contains an element of K+K+K for some fixed T in ![[3 \log S, 3 \log S + 3 \log 2]](https://s0.wp.com/latex.php?latex=%5B3+%5Clog+S%2C+3+%5Clog+S+%2B+3+%5Clog+2%5D&bg=ffffff&fg=000000&s=0&c=20201002) , e.g.
, e.g.  .
.
On the one hand, this is quite a narrow interval to hit. On the other hand, K+K+K has about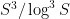 triples in it, so probabilistically one has quite a good chance of catching something. But, as always, the difficulty is to get a deterministic result which works even in the worst case scenario.
triples in it, so probabilistically one has quite a good chance of catching something. But, as always, the difficulty is to get a deterministic result which works even in the worst case scenario.
Presumably the thing to do now is fire up the circle method and write things in terms of the Fourier coefficients of K, which assuming RH should be quite small (of size about , ignoring logs). The fact that
, ignoring logs). The fact that  is not as small as
is not as small as 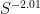 is a little worrying, though. (And things seem to get progressively worse as the number of sums increases.) But perhaps there is a way to tweak the method to do better. (For instance, we don't need ''all'' the factors of the number to be between S and 2S; just having one of them like that would be enough.)
is a little worrying, though. (And things seem to get progressively worse as the number of sums increases.) But perhaps there is a way to tweak the method to do better. (For instance, we don't need ''all'' the factors of the number to be between S and 2S; just having one of them like that would be enough.)
Comment by Terence Tao — August 9, 2009 @ 4:27 am |
Hmm, the tininess of the interval [T,T+S^{-2.01}] is quite discouraging. Even if one considers the larger set K + L, where L is the log-integers (and which are very highly uniformly distributed), one can still miss this interval entirely. Undoing the logarithm, the point here is that an interval of the form [N, N+S^{0.99}] could manage, by a perverse conspiracy, to miss all multiples of p for every prime p between S and 2S. (Indeed, by the Chinese remainder theorem, we know that there exists some huge N – exponentially large perhaps – for which this is the case. Also, N=1 would also work :))
But perhaps we could show by more number-theoretic means that this would not happen for polynomially-sized N. For instance, suppose somehow that [S^2, S^2+S^{0.99}] managed to avoid all multiples of primes p between S and 2S. This would mean that the residues -S^2 \hbox{ mod } p managed to avoid the large interval [0,S^{0.99}] for all such p. If one had an equidistribution result for these residues then one could perhaps get a contradiction, but I don’t see how to get this – I know of few tools for correlating residues in one modulus with residues in another (other than quadratic reciprocity, which doesn’t seem to be applicable here.)
Comment by Terence Tao — August 9, 2009 @ 2:39 pm |
Hmm, the tininess of the interval [T,T+S^{-2.01}] is quite discouraging. Even if one considers the larger set K + L, where L is the log-integers (and which are very highly uniformly distributed), one can still miss this interval entirely. Undoing the logarithm, the point here is that an interval of the form [N, N+S^{0.99}] could manage, by a perverse conspiracy, to miss all multiples of p for every prime p between S and 2S. (Indeed, by the Chinese remainder theorem, we know that there exists some huge N – exponentially large perhaps – for which this is the case. Also, N=1 would also work :))
It might be instructive to state this as a negative result. I’ll take a stab at it, though I’m probably not the best person to do so, but it’ll at least be instructive to me. Stated as an obstruction, this says that even augmented with “Additive Combinatorics Lite” (in this case, Fourier analysis), sieve-theoretic methods don’t suffice to produce a small interval with non-smooth numbers. Am I close?
Comment by Harrison — August 9, 2009 @ 11:23 pm |
Yes, I think this is the case, although the obstruction is not really formalised yet.
Here is a back-of-the-envelope Fourier calculation which looks a bit discouraging. Suppose one wants to show that the interval![[2N^3, 2N^3+N^{0.99}]](https://s0.wp.com/latex.php?latex=%5B2N%5E3%2C+2N%5E3%2BN%5E%7B0.99%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) contains an element of the triple product set
contains an element of the triple product set ![[N,2N] \cdot [N,2N] \cdot [N,2N]](https://s0.wp.com/latex.php?latex=%5BN%2C2N%5D+%5Ccdot+%5BN%2C2N%5D+%5Ccdot+%5BN%2C2N%5D&bg=ffffff&fg=000000&s=0&c=20201002) . If we let
. If we let 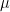 be counting measure on the log-integers
be counting measure on the log-integers  , we are asking that
, we are asking that 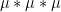 gives a non-zero weight to the the interval
gives a non-zero weight to the the interval ![[\log 2N^3, \log 2N^3 + O( N^{-2.01} ) ]](https://s0.wp.com/latex.php?latex=%5B%5Clog+2N%5E3%2C+%5Clog+2N%5E3+%2B+O%28+N%5E%7B-2.01%7D+%29+%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
We express this Fourier-analytically, basically as a Fourier integral of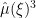 over an interval
over an interval  , multiplied by the normalising factor of
, multiplied by the normalising factor of 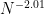 .
.
The main term will be coming from the low frequencies , where
, where 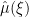 is about N; this gives the main term of about
is about N; this gives the main term of about  , which is what one expects.
, which is what one expects.
What about the error terms? Well, the Dirac spikes of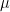 are distance about 1/N apart. For $N \ll |\xi| \ll N^{2.01}$, there’s no particular reason for any coherence in the Fourier sum in
are distance about 1/N apart. For $N \ll |\xi| \ll N^{2.01}$, there’s no particular reason for any coherence in the Fourier sum in 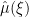 , and so I would expect the sum to behave randomly, i.e.
, and so I would expect the sum to behave randomly, i.e.  in this region. (In fact, RH basically would give this to us). This leads one to an error term of
in this region. (In fact, RH basically would give this to us). This leads one to an error term of  , which is too large compared to the main term.
, which is too large compared to the main term.
The situation does not seem to improve with various tweaking of parameters, though maybe I’m missing something.
Comment by Terence Tao — August 10, 2009 @ 12:19 am |
[…] discussion threads polymath4, devoted to finding deterministically large prime numbers, is on its way on the polymath […]
Pingback by Polymath4 – Finding Primes Deterministically – is On Its Way « Combinatorics and more — August 9, 2009 @ 6:58 am |
Google gives it secondhand that there’s no known unconditional, deterministic polynomial-time algorithm for squarefreeness (although the cited paper is 15 years old.)
My hunch is that testing squarefreeness is hard, although of course it’s trivial with a factoring oracle, so it’s unlikely to be NP-complete or anything. If you try to get much more information than whether n is squarefree, by the way (for instance, if you want to find the exponents of the primes that divide n), you start to get reductions from problems that are almost certainly intractable.
I’m also not convinced that a polynomial-time, or even random polynomial-time, reduction from factoring to squarefreeness exists, however, although the following heuristic argument hints at what such a reduction would probably look like. Since the squarefree numbers have positive density, testing a number of any size for squarefreeness essentially provides one bit of information; however, writing down the prime factorization of a k-digit integer requires O(log k) bits in general, so a reduction would probably have to make O(k) calls to SQUAREFREE.
Squarefreeness also seems to have some connections to the Euclidean algorithm, which essentially derives from the fact that squarefree numbers are characterized by the property that in any factorization n = a*b, a and b are coprime. (My first stab at trying to reduce factoring to squarefreeness was along the following lines: if n is squarefree, then pick a number N >> n that’s also squarefree [this can be done randomly w.h.p.], and test N*n for squarefreeness to find common factors. But of course the last step can be done via the Euclidean algorithm just as well.) It’d be interesting to see if we can make those connections more rigorous.
Comment by Harrison — August 9, 2009 @ 8:46 am |
Warning: This post is crazy long, way longer than I expected, as I had a few realizations that led to more realizations as I wrote it. Apologies.
Also on the squarefree front, I’d like to toss out another toy problem, which is related (though not really comparable) to the initial problem of whether we can find consecutive squarefree integers.
Problem 5a, Boring Preliminary Version. Show that there exist arbitrarily long arithmetic progressions of squarefree integers.
What’s that, you say? The squarefree integers have positive density — really big positive density! — and so by Szemeredi’s theorem, there are arbitrarily long APs? Well, yeah, but that’s boring. The meta-question we’re really after is how we can take advantage of the structure of the squarefree numbers, and Szemeredi’s theorem throws away all of that structure. So let’s tie one hand behind our collective back:
Problem 5a (Open). Without using Szemeredi’s theorem or some moral equivalent, show that there exist arbitrarily long APs of squarefree integers.
This is much more like what we really want. It’s worth noting that van der Waerden’s theorem isn’t sufficient to solve 5a, since we can embed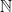 with its additive structure into the squareful numbers (consider the sequence 4, 8, 12, 16, …) It’s also probably useful to note that the squarefree numbers are a good example of a set which is neither fully pseudorandom nor highly structured; for instance, there are no quadruples of consecutive squarefree numbers (since one of them would be divisible by 4), which isn’t true for random sets of positive density; but neither is there an infinite AP, which is the easiest structure to take advantage of. On the pseudorandom hand, the distribution of squarefree numbers is what we’d expect from a random sequence of density
with its additive structure into the squareful numbers (consider the sequence 4, 8, 12, 16, …) It’s also probably useful to note that the squarefree numbers are a good example of a set which is neither fully pseudorandom nor highly structured; for instance, there are no quadruples of consecutive squarefree numbers (since one of them would be divisible by 4), which isn’t true for random sets of positive density; but neither is there an infinite AP, which is the easiest structure to take advantage of. On the pseudorandom hand, the distribution of squarefree numbers is what we’d expect from a random sequence of density  , with the error term bounded by
, with the error term bounded by 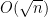 . On the structured hand, assuming the Riemann hypothesis, we can cut the exponent in the error term to just under 1/3.
. On the structured hand, assuming the Riemann hypothesis, we can cut the exponent in the error term to just under 1/3.
I’d also like to mention two variations of this problem, the first of which is easier and the last of which is probably harder.
Problem 5a, Variation 1 (Easy). Show (without using Roth’s theorem or equivalent) that there are infinitely many triples of squarefree numbers in arithmetic progression; equivalently, show that there are infinitely many solutions in squarefree numbers to x + y = 2z.
Note that there aren’t quite enough squarefrees for a union-bound proof that there are infinitely many consecutive squarefree triples; it’s probably true that there are infinitely many, and this might not even be that hard to prove, but I can find neither a proof that there are infinitely many squarefree triples nor any indication of the problem’s status.
However, the problem as stated above has an easy solution which I just thought of. Note that 3, 5, 7 is a 3-term AP of squarefree numbers. Now let p > 7 be prime; then 3p, 5p, 7p is another squarefree AP. We can turn any k-term AP of squarefrees into an infinite family of APs in the same way. Unfortunately this has no direct bearing on the initial toy problem (to find consecutive squarefree numbers), since the symmetry we’re exploiting here doesn’t preserve consecutiveness.
Problem 5a, Variation 2 (Easy). Explicitly exhibit a polynomial-time computable family of 3-term APs of squarefree numbers. (i.e., given an integer n, construct in polynomial time a sequence x, y, z of squarefree numbers with n < x < y < z and x + z = 2y.)
Actually, essentially the above construction works here, too — just replace p by 2*11*…*k, where k is a prime about log n. So I'll introduce a new problem to try to get rid of the freedom to multiply through by a large enough prime:
Problem 5b, Variations 0-2 (Open). Do Problem 5a and its variations hold with the additional constraint that the squarefree integers in the AP are mutually relatively prime?
These questions may be closest to the original toy problem 5; I could talk about them some, but this post is too long already, so I won’t.
Comment by Harrison — August 9, 2009 @ 6:25 pm |
Well, one can use the W-trick to boost the density of square-free numbers to as close to 1 as desired, which should solve Problem 5a. More precisely, if W is the product of all the primes less than w, then the density of numbers n such that Wn+1 is square-free is asymptotically , which converges to 1 as
, which converges to 1 as 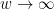 . To get progressions of length 100, one just has to take w large enough that the density of n with Wn+1 square-free is over 99%, in which case one gets progressions from the union bound.
. To get progressions of length 100, one just has to take w large enough that the density of n with Wn+1 square-free is over 99%, in which case one gets progressions from the union bound.
Getting an explicit, mutually coprime, progression seems harder though.
Comment by Terence Tao — August 9, 2009 @ 8:51 pm |
The solution to Problem 5a with pairwise coprime terms is an immediate consequence of results of L. Mirsky on patterns of squarefree integers. See
L. Mirsky, Arithmetical pattern problems relating to divisibility by r-th powers, Proc. London Math. Soc. (2), 50 (1949), 497-508.
L. Mirsky, Note on an asymptotic formula connected with r-free integers, Quart. J. Math., Oxford Ser., 18 (1947), 178-182″.
Mirsky identifies those tuples $k_1,\dots,k_s$ of integers for which $k_1 + n,\ldots,k_s + n$ are simultaneously squarefree (or r-free) for infinitely many $n$ (briefly, the obvious necessary condition is actually sufficient), and gives an asymptotic estimate for the number of such $n \leq x$. His arguments are elementary.
To produce infinitely many arithmetic progressions of $s$ terms consisting of pairwise coprime squarefrees using the result of Mirsky, let $a$ be the square of the product of the primes $p \sqrt{s}$ this is clear, since there aren’t enough of them, while they are all congruent to $1$ modulo $p^2$ for any prime $p \leq \sqrt{s} < s$ by the definition of $a$. Furthermore they are pairwise coprime, for if some prime $q$ divides two of them, it divides their difference, which is of the form $(n – m)a$ with $0 \leq m < n \leq s – 1$. Then $q$ is a prime less than $s$ by the definition of $a$, but this is impossible since all the $k_j = 1 + ja$ are congruent to $1$ modulo such primes. Now it follows that $1 + n,1 + a + n,1 + 2a + n,\dots,1 + (s-1)a + n$ are coprime and simultaneously squarefree infinitely often by Mirsky's results.
Comment by Anon — August 10, 2009 @ 8:20 pm |
The existence of arbitrarily long arithmetic progressions of pairwise coprime squarefrees is an immediate consequence of results of L. Mirsky. See
L. Mirsky, Arithmetical pattern problems relating to divisibility by $r$th powers, Proc. London Math. Soc. (2), 50 (1949), 497-508.
L. Mirsky, Note on an asymptotic formula connected with $r$-free integers, Quart. J. Math., Oxford Ser., 18 (1947), 178-182.
Comment by Anon — August 10, 2009 @ 9:04 pm |
According to Granville (“ABC Allows Us to Count Squarefrees”, p. 992), Hooley proved unconditionnally that there exists infinitely many consecutive squarefree triples. The point is to find squarefree values of the polynomial (n+1)(n+2)(n+3).
In fact the result of Hooley is more general and deals with squarefree values of f(n), where f is a degree 3 polynomial.
There is also a density statement. But I could not find a reference for a bound on the error term.
You can refer to the following articles for more information:
A. Granville, “ABC Allows Us to Count Squarefrees”,
Click to access polysq3.pdf
F. Pappalardi, “A survey on k-freeness”,
Click to access allahabad2003.pdf
Comment by François Brunault — August 11, 2009 @ 6:07 pm |
The integers 1,2,3 are squarefree, so by Mirsky’s result from 1947, there are infinitely many squarefree triples n+1,n+2,n+3. But I reckon that this case must have been known before Mirsky. The error bound of Mirsky is O(x^{2/3 + \epsilon}). Possibly this can be improved, since Heath-Brown obtained a better error bound for pairs n,n+1.
Comment by Anon — August 11, 2009 @ 8:30 pm |
6. Regarding Strategy 1, I’d like just to mention that there are some candidates for sequences which contain only primes on Sloane’s encyclopedia. Of course none of them is proved to contain only primes yet, but maybe one of them is actually tracatable by (or may inspire some) knowledgeable readers here.
A first (quite dense) sequence is A065296: prove that if there is only one solution in![[0,n-1]](https://s0.wp.com/latex.php?latex=%5B0%2Cn-1%5D&bg=ffffff&fg=000000&s=0&c=20201002) to
to  (namely
(namely 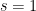 ), then
), then  is prime.
is prime.
Another (quite sparse) is A092571: explain which number of the form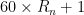 is prime (where
is prime (where 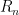 is the n-th repunit), the actual sequence being 61, 661, 6661, 6666666661, 666666666666666661, 666666666666666666661, 6666666666666666666661….
is the n-th repunit), the actual sequence being 61, 661, 6661, 6666666661, 666666666666666661, 666666666666666666661, 6666666666666666666661….
Comment by Thomas Sauvaget — August 9, 2009 @ 8:50 am |
Responding to Terry’s comment 3, I’d like to mention yet another toy problem. This one is designed to be an easier goal for the additive-combinatorial approach, but one that might conceivably help with the harder one. Recall that that approach is to take K to be the set of logarithms of all primes in some interval, and to try to prove that the iterated sumsets of K must become very dense. It seems to me that a good way of getting a bit of intuition about this problem would be to look instead at the set L of logarithms of all integers in some interval (whether prime or composite) and think about the same question for L.
Suppose that one could prove that the iterated sumsets of L eventually became very dense. Then one would have shown that in every small interval![[n,n+m]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2Bm%5D&bg=ffffff&fg=000000&s=0&c=20201002) there must be a number with a factor (but not necessarily a prime factor) in an interval
there must be a number with a factor (but not necessarily a prime factor) in an interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Here we are hoping for
. Here we are hoping for  to be very small, and for
to be very small, and for  not to be too small compared with
not to be too small compared with  (something like
(something like  seems about the best one can hope for, but initially one might settle for less than this). But
seems about the best one can hope for, but initially one might settle for less than this). But  isn’t too tiny compared with
isn’t too tiny compared with  — it might be
— it might be  , or
, or 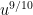 , say.
, say.
I’m pretty sure it’s not trivial that there must be a number between and
and  that has a factor in some given interval
that has a factor in some given interval ![[u,v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cv%5D&bg=ffffff&fg=000000&s=0&c=20201002) such as the above, but I haven’t checked. If it turns out to be obvious, then this is not after all an interesting problem. (As it is, a positive solution wouldn’t be all that interesting, except as an initial guide to how to prove the result when we replace L by K.)
such as the above, but I haven’t checked. If it turns out to be obvious, then this is not after all an interesting problem. (As it is, a positive solution wouldn’t be all that interesting, except as an initial guide to how to prove the result when we replace L by K.)
What I quite like about this problem is that the Fourier transform of the set L is a little piece of the Riemann zeta function. Indeed, the value at of the transform of the measure that sticks an atom of weight 1 at every point of L is
of the transform of the measure that sticks an atom of weight 1 at every point of L is 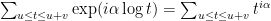 . This suggests to me that some of the techniques that have been used for analysing Dirichlet series could be used here.
. This suggests to me that some of the techniques that have been used for analysing Dirichlet series could be used here.
But there is also the possibility of using insights connected with sum-product problems. For instance, is a concave function and the interval
is a concave function and the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) has very good additive properties. It follows from results of Elekes (and others? my memory is failing me here) that
has very good additive properties. It follows from results of Elekes (and others? my memory is failing me here) that 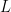 can’t have good additive properties. By that I mean that the sumset
can’t have good additive properties. By that I mean that the sumset 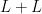 must be large. Something like this probably applies to
must be large. Something like this probably applies to  as well, but after a few more sums, since, at least if
as well, but after a few more sums, since, at least if  is linear in
is linear in  , the techniques that go into Vinogradov’s three-primes theorem will tell us that the set of primes in
, the techniques that go into Vinogradov’s three-primes theorem will tell us that the set of primes in ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) will, after a bounded number of sums, become pretty evenly distributed in an additively structured set.
will, after a bounded number of sums, become pretty evenly distributed in an additively structured set.
The remarks in the above paragraph aren’t directly relevant, but they are meant to be suggestive: if you take an arithmetic progression and take logs of everything, then you should have something that’s so unlike an arithmetic progression that when you take iterated sumsets it becomes far less atomic. It might even be that such a result followed from something much more general, where was replaced by an arbitrary convex function. (Actually, not quite arbitrary, but perhaps something that has a gradient that decreases reasonably steadily.)
was replaced by an arbitrary convex function. (Actually, not quite arbitrary, but perhaps something that has a gradient that decreases reasonably steadily.)
Comment by gowers — August 9, 2009 @ 2:29 pm |
This is not quite in the spirit of Tim’s approach, but I can get a non-trivial result on L+L using the Weyl bound for the Gauss circle problem, or more precisely the variant of this circle problem for the hyperbola (essentially the Dirichlet divisor problem).
More precisely, let’s look at the product set![[S,2S] \cdot [S,2S] \subset [S^2, 4S^2]](https://s0.wp.com/latex.php?latex=%5BS%2C2S%5D+%5Ccdot+%5BS%2C2S%5D+%5Csubset+%5BS%5E2%2C+4S%5E2%5D&bg=ffffff&fg=000000&s=0&c=20201002) in the middle of the interval
in the middle of the interval ![[S^2,4S^2]](https://s0.wp.com/latex.php?latex=%5BS%5E2%2C4S%5E2%5D&bg=ffffff&fg=000000&s=0&c=20201002) , say near
, say near  (this is like considering L+L where L are the log-integers restricted to
(this is like considering L+L where L are the log-integers restricted to ![[\log S, \log S + \log 2]](https://s0.wp.com/latex.php?latex=%5B%5Clog+S%2C+%5Clog+S+%2B+%5Clog+2%5D&bg=ffffff&fg=000000&s=0&c=20201002) ). It’s trivial that any interval of length S near
). It’s trivial that any interval of length S near  will meet
will meet ![[S,2S] \cdot [S,2S]](https://s0.wp.com/latex.php?latex=%5BS%2C2S%5D+%5Ccdot+%5BS%2C2S%5D&bg=ffffff&fg=000000&s=0&c=20201002) . I claim though that the same is true for intervals of size about
. I claim though that the same is true for intervals of size about 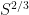 . The reason is that the number of products of the form
. The reason is that the number of products of the form ![[S,2S] \cdot [S,2S]](https://s0.wp.com/latex.php?latex=%5BS%2C2S%5D+%5Ccdot+%5BS%2C2S%5D&bg=ffffff&fg=000000&s=0&c=20201002) less than a given number x is basically the number of lattice points in the square
less than a given number x is basically the number of lattice points in the square ![[S,2S] \times [S,2S]](https://s0.wp.com/latex.php?latex=%5BS%2C2S%5D+%5Ctimes+%5BS%2C2S%5D&bg=ffffff&fg=000000&s=0&c=20201002) intersect the hyperbolic region
intersect the hyperbolic region  . The Weyl technology for the Gauss circle problem (Poisson summation, etc.) gives an asymptotic for this with an error of
. The Weyl technology for the Gauss circle problem (Poisson summation, etc.) gives an asymptotic for this with an error of  , which implies in particular that this count must increase whenever x increases by more than
, which implies in particular that this count must increase whenever x increases by more than  . So every interval of this length must contain at least one number which factors as a product of two numbers in [S,2S].
. So every interval of this length must contain at least one number which factors as a product of two numbers in [S,2S].
Presumably some of the various small improvements to the Weyl bound for the circle problem over the years can be transferred to the hyperbola, allowing one to reduce the 2/3 exponent slightly.
Unfortunately the asymptotics become much much worse if we restrict the numbers in [S,2S] to be prime, so I doubt this gives anything particularly non-trivial for the original primality problem. Also the error term in these lattice point problems is never going to be better than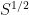 , so we once again butt our heads against this
, so we once again butt our heads against this 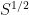 barrier.
barrier.
Comment by Terence Tao — August 9, 2009 @ 7:20 pm |
I’ve just had another thought, and in the Polymath spirit I’m going to express it before thinking at all seriously about whether it has a chance of being true. (Or rather, later in this comment I’ll think about that in real time, so to speak, and quite likely not manage to resolve the problem.)
The question is this. I’ll repeat the set-up from my previous comment (number 7). Let be an integer and let
be an integer and let  be a power of
be a power of  . Let
. Let  be an integer that’s quite a bit smaller than
be an integer that’s quite a bit smaller than  — something like
— something like  (a function chosen because the number of prime factors of a typical integer is
(a function chosen because the number of prime factors of a typical integer is  so one might expect their typical size to be about
so one might expect their typical size to be about  ). One thing we’d very much like to be able to do is show that some number in the interval
). One thing we’d very much like to be able to do is show that some number in the interval ![[n,n+m]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2Bm%5D&bg=ffffff&fg=000000&s=0&c=20201002) has a prime factor of size roughly
has a prime factor of size roughly  . Let’s take that to mean that it has a prime factor between
. Let’s take that to mean that it has a prime factor between  and
and 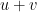 , where
, where  , though I’m open to other choices for
, though I’m open to other choices for  . In the previous comment I suggested going for any factor in that interval, which would be a strictly easier problem. Now it occurs to me that we could be daring and go for a strictly harder problem: perhaps the conclusion is true for an arbitrary subset of
. In the previous comment I suggested going for any factor in that interval, which would be a strictly easier problem. Now it occurs to me that we could be daring and go for a strictly harder problem: perhaps the conclusion is true for an arbitrary subset of ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) of density
of density 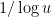 . That is, if
. That is, if ![B\subset [u,u+v]](https://s0.wp.com/latex.php?latex=B%5Csubset+%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) is a set of size at least
is a set of size at least  , then perhaps there is guaranteed to be an integer in
, then perhaps there is guaranteed to be an integer in ![[n,n+m]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2Bm%5D&bg=ffffff&fg=000000&s=0&c=20201002) with a factor in
with a factor in  .
.
A first check would obviously be to take to be a subinterval of
to be a subinterval of ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) of that size. Let
of that size. Let 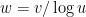 . We’ll be in trouble if it is not the case that
. We’ll be in trouble if it is not the case that  , since then the sets of powers of elements of
, since then the sets of powers of elements of  will leave huge gaps. So we find ourselves wanting to know whether
will leave huge gaps. So we find ourselves wanting to know whether  could be comparable to
could be comparable to  . But
. But  , so
, so 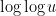 is comparable to
is comparable to  , which means we have no chance here.
, which means we have no chance here.
The obvious next question is how big would have to be for us to have a chance of proving something so general. The above analysis tells us that we need
would have to be for us to have a chance of proving something so general. The above analysis tells us that we need  to be at least
to be at least 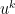 for a power
for a power  that's around
that's around 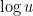 . But that's actually pretty good news, since the number of digits of
. But that's actually pretty good news, since the number of digits of 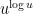 is about
is about  .
.
So here's a first refinement of the insane idea above: perhaps if you pick an arbitrary subset of
of ![[u,v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cv%5D&bg=ffffff&fg=000000&s=0&c=20201002) of density at least
of density at least 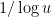 , and
, and  is significantly bigger than
is significantly bigger than 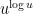 , then some number in the interval
, then some number in the interval ![[n,n+(\log n)^{100}]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2B%28%5Clog+n%29%5E%7B100%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) must have a factor in
must have a factor in  .
.
What I like about this (unless it is trivially false) is that it is very general and therefore could be easier to tackle than something about the primes. It suggests a strategy, which is first to tackle the case where![B=[u,v]](https://s0.wp.com/latex.php?latex=B%3D%5Bu%2Cv%5D&bg=ffffff&fg=000000&s=0&c=20201002) and then to look at arbitrary subsets of reasonable density.
and then to look at arbitrary subsets of reasonable density.
Comment by gowers — August 9, 2009 @ 4:41 pm |
To make this conjecture sound more plausible, let me give a heuristic argument for it.
1. The interval![J=[u,v]](https://s0.wp.com/latex.php?latex=J%3D%5Bu%2Cv%5D&bg=ffffff&fg=000000&s=0&c=20201002) is a highly “additive set” and therefore should spread out very evenly from a multiplicative point of view. (Equivalently,
is a highly “additive set” and therefore should spread out very evenly from a multiplicative point of view. (Equivalently,  is very far from additive.) So the conjecture seems pretty likely in the case
is very far from additive.) So the conjecture seems pretty likely in the case 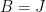 . (However, serious thought needs to go into just how dense we think we can prove that iterated sumset will be. One possibility here might be to use the fact that the derivative of
. (However, serious thought needs to go into just how dense we think we can prove that iterated sumset will be. One possibility here might be to use the fact that the derivative of 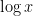 decreases very smoothly to prove that
decreases very smoothly to prove that  has lots of parts that resemble arithmetic progressions of all sorts of different common differences. So the sumset should be beautifully spread out. I wonder if this is already a point where somebody ought to go off, do some private calculations, and report back. I could give it a go, but as ever I would like to ask others what they think first.)
has lots of parts that resemble arithmetic progressions of all sorts of different common differences. So the sumset should be beautifully spread out. I wonder if this is already a point where somebody ought to go off, do some private calculations, and report back. I could give it a go, but as ever I would like to ask others what they think first.)
2. If we take a subset of
of 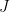 of density
of density 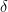 , then we would expect any gaps in
, then we would expect any gaps in 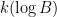 to be filled once
to be filled once  got to around
got to around 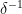 . For instance, if you take a subset of
. For instance, if you take a subset of  of density
of density 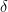 , then after about
, then after about 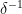 sums it starts to be pretty evenly spread around the whole of
sums it starts to be pretty evenly spread around the whole of  . Obviously a subset of
. Obviously a subset of 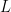 isn’t quite so simple, but something similar ought to happen “near the middle”.
isn’t quite so simple, but something similar ought to happen “near the middle”.
Comment by gowers — August 9, 2009 @ 5:34 pm |
My worry is that if one discretises at the correct scale, that J is actually quite sparse and so it will take a long time to achieve the desired mixing.
More precisely, in the logarithmic scale, the interval [n,n+m] has length about . So one would need to discretise at roughly the scale 1/n in order to make things work. Meanwhile, the interval [u,v] has length about 1, so when one discretises is sort of like an arithmetic progression of length n. But J only fills up about u of this progression. u is like
. So one would need to discretise at roughly the scale 1/n in order to make things work. Meanwhile, the interval [u,v] has length about 1, so when one discretises is sort of like an arithmetic progression of length n. But J only fills up about u of this progression. u is like 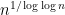 , so it’s rather sparse. In particular, it’s smaller than any power of n, which tends to be a warning sign for Fourier-analytic methods – Plancherel’s theorem, in particular, permits quite a large number of very large Fourier coefficients, which is not promising. Admittedly, one is taking a large iterated sumset of J, but my initial guess is that the parameters are not favorable. It’s worth doing a back-of-the-envelope calculation to confirm this, of course. (Note also that we don’t necessarily have to shoot for m as small as polylog(n) to declare progress; m could be as large as
, so it’s rather sparse. In particular, it’s smaller than any power of n, which tends to be a warning sign for Fourier-analytic methods – Plancherel’s theorem, in particular, permits quite a large number of very large Fourier coefficients, which is not promising. Admittedly, one is taking a large iterated sumset of J, but my initial guess is that the parameters are not favorable. It’s worth doing a back-of-the-envelope calculation to confirm this, of course. (Note also that we don’t necessarily have to shoot for m as small as polylog(n) to declare progress; m could be as large as 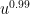 (say) and we would still have something beating the trivial bound.) But even with this relaxation of the problem, J looks dangerously sparse to me…
(say) and we would still have something beating the trivial bound.) But even with this relaxation of the problem, J looks dangerously sparse to me…
Comment by Terence Tao — August 10, 2009 @ 12:08 am |
K. Ford has a big paper in Annals (available at http://front.math.ucdavis.edu/0401.5223 ) which gives information about the asymptotic behavior of the number of integers up to with at least one divisor in an interval
with at least one divisor in an interval ![[y,z]](https://s0.wp.com/latex.php?latex=%5By%2Cz%5D&bg=ffffff&fg=000000&s=0&c=20201002) , more or less for arbitrary
, more or less for arbitrary 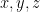 . He does state a result (Th. 2, page 6 of the arXiv PDF) with
. He does state a result (Th. 2, page 6 of the arXiv PDF) with  restricted to an interval
restricted to an interval ![[x-\Delta,x]](https://s0.wp.com/latex.php?latex=%5Bx-%5CDelta%2Cx%5D&bg=ffffff&fg=000000&s=0&c=20201002) , but
, but 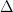 must be quite large (something like
must be quite large (something like  in the setting of the previous comment); he does say that the range of
in the setting of the previous comment); he does say that the range of 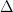 can be improved, but to get a power of log seems hard. However, the techniques he develops could be useful.
can be improved, but to get a power of log seems hard. However, the techniques he develops could be useful.
Comment by Emmanuel Kowalski — August 10, 2009 @ 1:29 am |
In a similar spirit to the oracle example of “generic primes” which elude deterministic polynomial time
algorithms (posted on the wiki), I think we have to be careful here too. I was thinking about the
following example. Consider the interval [n,n+m] where n=2^k is a power of 2. This way, all the
elements in this interval are “simple”, ie have Kolmogorov complexity at most log log n + log m.
Now consider an interval U=[u,2u] where say u=n^(1/t). So in Tim’s scenario we had t about
sqrt(log n). Take as the subset B of U the primes in U which have Kolmogorov complexity at least
log(u)/2log log(u) even relative to the set U. This is still a set with density
at least 1/2log(u). Suppose that an element v of B divided an element x in [n,n+m]. Then we could
describe v given the set U by specifying x, and with log t more bits identify v in the list of at most t
elements of U which divide x. Thus we must have log(u)/2log log(u) <= log log n + log m + log t, or
in other words roughly n <= (3mt log n)^t. This seems to rule out having t like sqrt(log n) and m
polylogarithmic in n.
Comment by Troy — August 10, 2009 @ 10:56 pm |
I found this reference to a paper on the discussion thread.
Proceedings of the London Mathematical Society 83, (2001), 532–562.
R. C. Baker, G. Harman and J. Pintz, The difference between consecutive primes, II
The authors sharpen a result of Baker and Harman (1995), showing that [x, x + x^{0.525}] contains prime numbers for large x.
It looks like using this we can find a prime in O(10^k)^{0.525} time.
Comment by kristalcantwell — August 9, 2009 @ 5:03 pm |
Tim’s ideas on sumsets of logs got me to thinking about a related, but different approach to these sorts of “spacing problems”: say we want to show that no interval [n, n + log n] contains only (log n)^100 – smooth numbers. If such strange intervals exist, then perhaps one can show that there are loads of distinct primes p in [(log n)^10, (log n)^100] that each divide some number in this interval (we would need to exclude the possibility that the interval contains numbers divisible by primes to high powers to do this). Let’s assume this is true. And let’s say we have something like Omega( log n/ loglog n) of these primes dividing each number in our interval [n, n + log n], resulting in something like (log n)^{2 – o(1)} primes in total dividing numbers in this interval.
Now, given such a collection of primes, say they are p_1, …, p_k, where perhaps k ~ (log n)^{2-o(1)} or something, it is reasonable to expect that the set of sums
S := {c_1/p_1 + … + c_k/p_k : c_i = 0, 1, or -1}
is fairly dense in some not-too-short interval centered about 0 — so dense that we would expect that if q is any prime at all in [2,(log n)^100], then we can approximate
1/q = c_1/p_1 + … + c_k/p_k + E,
to an error E satisfying |E| < 1/n (log n)^100, say. If so, then multiplying through by n we would get
n/q = c_1 n/p_1 + … + c_k n/p_k + O( (log n)^{-100}).
But because each p_i divides a number in [n, n + log n], we would have that the RHS comes within something like O(k (log n)/max_i p_i) = O( (log n)^{-7}) of an integer. So, looking at the LHS we have q divides some number in the interval [n-q (log n)^{-7}, n + q (log n)^{-7}]. But this can't be possible for every prime q in [ (log n)^10, (log n)^100] by simple upper bounds on the number of prime divisors of numbers in short intervals.
Comment by Anonymous — August 9, 2009 @ 5:48 pm |
This probably counts as cheating, but one can get a little bit of traction if one assumes the ABC conjecture.
Consider the interval![[n, n+\log n/2]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n%2B%5Clog+n%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) where n is very smooth, say a power of 2, and suppose that all numbers were S-smooth. Assuming ABC, this shows that the radical (the product of all the prime factors) of any other element of
where n is very smooth, say a power of 2, and suppose that all numbers were S-smooth. Assuming ABC, this shows that the radical (the product of all the prime factors) of any other element of ![[n, n+\log n/2]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n%2B%5Clog+n%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) is
is 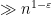 for any fixed
for any fixed  . In particular, all such numbers contain
. In particular, all such numbers contain  prime factors that are greater than
prime factors that are greater than  . But no two elements in
. But no two elements in ![[n, n+\log n/2]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n%2B%5Clog+n%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) can share a common prime factor greater than
can share a common prime factor greater than  , so we must have
, so we must have 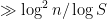 prime factors less than S. But this is only compatible with the prime number theorem if
prime factors less than S. But this is only compatible with the prime number theorem if  . Thus we must have an element of
. Thus we must have an element of ![[n, n+\log n/2]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n%2B%5Clog+n%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) which has a prime factor
which has a prime factor 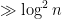 . So, using ABC, one can match the RH bound (which gives us a prime of size at least
. So, using ABC, one can match the RH bound (which gives us a prime of size at least 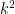 after k tries). I don’t see how to use the ABC conjecture to get beyond the exponent 2, though.
after k tries). I don’t see how to use the ABC conjecture to get beyond the exponent 2, though.
Comment by Terence Tao — August 9, 2009 @ 6:00 pm |
I think perhaps the interval [(log n)^10, (log n)^100] in my comment can be replaced with something like [ (log n)^(2 + epsilon), (log n)^100], through limiting k to size a little larger than log n, say k ~ (log n)^(1 + eps/2) or something — i.e. we don’t use all the prime divisors of numbers in [n,n+log n]. Getting this interval somewhat below (log n)^2 (so that the method need not require heavy conjectures like ABC) might well require generalizing the problem somewhat. I will think about it…
Also, I thought I would point out that for the method to work it isn’t necessary for every fraction 1/q to be well-approximated by elements of S — it really only suffices that a substantial number of primes q < (log n)^100 have this property. A subproblem to see whether the method has any chance of succeeding would be to show that there is some not-too-short interval near 0, such that every point of that interval comes within 1/n (log n)^100 of some point of S, for any set S generated using an arbitrary subset of something like (log n)^{1+epsilon} primes in [(log n)^2, (log n)^100].
Setting aside the need to close the gap between (log n) and (log n)^2 (as could be done by appealing to ABC), it seems that the method has some advantages and disadvantages to Tim's sums-of-logs approach: first, the method doesn't require one to show strong uniform distribution-type results everywhere (e.g. it doesn't require this for all n) — it only requires that the set of sums S come close to just enough fractions 1/q. On the other hand, it has the huge disadvantage of requiring one to work with arbitrary sets of primes p_1,…,p_k, which might not include all the first few 2,3,…,p_t (which the sums-of-logs approach uses).
Comment by Anonymous — August 9, 2009 @ 9:57 pm |
It occurred to me just yesterday that it isn’t necessary to approximate numbers for “many”
for “many”  — I think it is only necessary that one can approximate many such fractions for
— I think it is only necessary that one can approximate many such fractions for 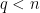 , unless I am missing something obvious. If so, then it would make it a lot easier a condition to satisfy.
, unless I am missing something obvious. If so, then it would make it a lot easier a condition to satisfy.
Also, perhaps a viable approach to showing that these fractions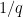 can be so well approximated would be to show that the set
can be so well approximated would be to show that the set  contains some quite long “near-progressions'' — i.e. there is a very long arithmetic progression such that every element in it comes very, very close to an element of
contains some quite long “near-progressions'' — i.e. there is a very long arithmetic progression such that every element in it comes very, very close to an element of  , which would show that
, which would show that  has a highly regular substructure. If this can be proved, then perhaps one can show that there are lots of fractions
has a highly regular substructure. If this can be proved, then perhaps one can show that there are lots of fractions 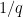 that come close to some points of this long progression, and therefore are well-approximated by elements of
that come close to some points of this long progression, and therefore are well-approximated by elements of  .
.
Perhaps inverse Littlewood-Offord type results can be used somehow.
Comment by Anonymous — August 10, 2009 @ 3:44 pm |
I quite like this approach – it uses the entire set S of sums of the 1/p_i, rather than a finite sumset of the log-integers or log-primes, and so should in principle get the maximal boost from additive combinatorial methods. It’s also using the specific properties of the integers more intimately than the logarithmic approach, which is perhaps a promising sign.
The one thing is that we are starting with a set of size
of size  and trying to show that the sumset mixes to an accuracy of about
and trying to show that the sumset mixes to an accuracy of about 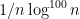 , which is roughly of the shape
, which is roughly of the shape  . This is moderately scary but still plausible (there are, after all,
. This is moderately scary but still plausible (there are, after all, 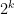 sums to play with here). Presumably a good place to start would be to try to show mixing to accuracy
sums to play with here). Presumably a good place to start would be to try to show mixing to accuracy 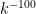 first. I’ll think about this…
first. I’ll think about this…
Comment by Terence Tao — August 9, 2009 @ 11:53 pm |
I think I can find two consecutive square free k-digit numbers in (10^(k+1)^1/3 time given factoring.
The idea is that for 10^k to 10^k + (10^(k+1)^1/3) we sieve out the numbers divisible by 4 the remaining numbers square free numbers will have density roughly .8 plus an error term the maximum density without consecutive numbers is 2/3 so the error term must take care of at least .1
of the remaining numbers but the error term is known to be x^(17/54+ epsilon) see
http://en.wikipedia.org/wiki/Square-free_integer
and so will be bounded by the .1 of the remaining numbers so we will have two consecutive numbers in the interval and given factoring we can test every number in the interval and find them.
Comment by Kristal Cantwell — August 9, 2009 @ 6:07 pm |
Technically, the 17/54 exponent only applies if you assume RH; unconditionally,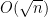 is the best known error term. So the algorithm only runs in
is the best known error term. So the algorithm only runs in  time without RH.
time without RH.
Comment by Harrison — August 9, 2009 @ 6:29 pm |
Regarding toy problems, I am not sure if problem 5 is a toy problem for our problem or the other way around since testing primality is in polynomial in the number of digits which seems like a serious restriction after all.
Noam offered some genuinly toy problems in
and I wonder if something can be done about them and if more toy problems of this nature can be found.
Comment by Gil Kalai — August 9, 2009 @ 7:06 pm |
As Terry pointed out, Noam’s problem 1 is doable via the Chinese Remainder Theorem. (The solution, as a sanity check: Just pick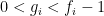 , and compute x with
, and compute x with 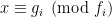 for all i; then x, x+1 has the desired property.)
for all i; then x, x+1 has the desired property.)
What strikes me is that the easy solution to Noam's problem of computing large "finitary primes" takes advantage of essentially the same symmetry as the easy way to find large squarefree integers. (I'm using "symmetry" in a very loose sense here.) The trick in both cases is to notice that if you have a finitary prime (resp. squarefree integer), then multiplying it by a prime gives you a new, larger finitary prime/squarefree number, in all but a very small number of degenerate cases which can be easily detected (in the case of finitary primes, by checking them against the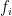 ; for squarefree numbers, via the Euclidean algorithm). In both cases, the problem becomes harder when you introduce a constraint that isn't preserved by this symmetry; namely, the property that two numbers are consecutive. So it's interesting, then, that the problem of finding consecutive finitary primes has a Sun Tzu solution; is there a "CRT result" for squarefree numbers as well?
; for squarefree numbers, via the Euclidean algorithm). In both cases, the problem becomes harder when you introduce a constraint that isn't preserved by this symmetry; namely, the property that two numbers are consecutive. So it's interesting, then, that the problem of finding consecutive finitary primes has a Sun Tzu solution; is there a "CRT result" for squarefree numbers as well?
Comment by Harrison — August 9, 2009 @ 7:35 pm |
Here are the two problems:
Problem 1: given m integers f_1 … f_m, with f_i \ge 3 for all i, and a desired length $n$, output an n-bit number x such that neither x nor x+1 is divisible by any of the f_i’s.
Problem 2: Find an n-bit integer x such that 2^x = 2 (mod x).
Comment by kristalcantwell — August 9, 2009 @ 8:14 pm |
Here’s a small rambling thought about trying in an utterly elementary way to produce a number close to by multiplying together numbers in the interval
by multiplying together numbers in the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) (see comment 8 for the rough magnitudes of
(see comment 8 for the rough magnitudes of  and
and  in terms of
in terms of  ).
).
We shall do it by starting with a very crude method and then trying to improve it bit by bit.
From the way we’ve chosen , we know that there must be some integer
, we know that there must be some integer  in the interval
in the interval ![[u+v/3,u+2v/3]](https://s0.wp.com/latex.php?latex=%5Bu%2Bv%2F3%2Cu%2B2v%2F3%5D&bg=ffffff&fg=000000&s=0&c=20201002) and an integer
and an integer  such that
such that 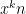 .
.
Method 1. Pick some pretty random bunch of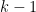 numbers in the interval
numbers in the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) in order to get a number
in order to get a number  such that
such that  . Then pick the smallest
. Then pick the smallest ![x\in[u,u+v]](https://s0.wp.com/latex.php?latex=x%5Cin%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that
such that  . This will get us to within
. This will get us to within  of
of 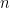 . But
. But  is around
is around  , which is not a very good approximation, but it is a start.
, which is not a very good approximation, but it is a start.
Method 2. This time we start with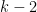 numbers and try to choose the last two numbers carefully. This problem is of course equivalent to approximating a number that lies squarely between
numbers and try to choose the last two numbers carefully. This problem is of course equivalent to approximating a number that lies squarely between  and
and  by a product of two numbers in the interval
by a product of two numbers in the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) . So let’s start with method 1: that is, we pick a number
. So let’s start with method 1: that is, we pick a number  and then try to find the best
and then try to find the best  . Suppose the result is
. Suppose the result is  . Now we’d like to make an adjustment. If we replace
. Now we’d like to make an adjustment. If we replace  and
and  by
by 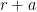 and
and  , then the result will be
, then the result will be 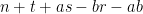 . How can we make that small? Well, we could start by finding small
. How can we make that small? Well, we could start by finding small  and
and 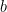 such that
such that 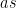 is very close to
is very close to  . If we then replaced those by
. If we then replaced those by 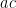 and
and  , the result would be
, the result would be 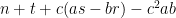 . If
. If 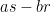 is smaller than
is smaller than  , then this allows us to reduce
, then this allows us to reduce 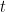 to some power.
to some power.
This is getting slightly messy, but maybe it’s enough to make it look possible that elementary arguments could show the existence of a pretty good approximation.
Actually, to continue an earlier but related thought, one could start by picking a bunch of numbers that get you into the right ball park. Call those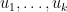 . Now we can make adjustments to the product and turn it into
. Now we can make adjustments to the product and turn it into  . If the
. If the 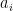 are kept very small, then the … hmm, no, this is running into problems because even if you can make the linear term small, the quadratic term will still be fairly big.
are kept very small, then the … hmm, no, this is running into problems because even if you can make the linear term small, the quadratic term will still be fairly big.
In the end, this comment hasn’t amounted to much, but I’ll post it all the same, in case it provokes anyone else to have more systematic thoughts along these lines.
Comment by gowers — August 9, 2009 @ 7:16 pm |
Re the penultimate paragraph in this comment, I realized down below that it’s better to take logs because then the problem is linearized. Or equivalently you concentrate not on the difference it makes when you replace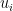 by
by  but on the factor that you multiply by. The hope would be that these ratios were sufficiently independent that you could find a subset of them that mutliplied to a ratio that got you significantly closer to
but on the factor that you multiply by. The hope would be that these ratios were sufficiently independent that you could find a subset of them that mutliplied to a ratio that got you significantly closer to 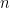 .
.
Comment by gowers — August 10, 2009 @ 12:07 am |
Regarding the square-free problem, there is a bound of Heath-Brown (D.R. Heath-Brown, The square sieve and consecutive square-free numbers, Math. Ann. 266 (1984), 251-259.) that states . Assuming a square-free testing oracle, I think this should give us a
. Assuming a square-free testing oracle, I think this should give us a  time algorithm.
time algorithm.
Comment by Mark Lewko — August 9, 2009 @ 8:39 pm |
[…] The Polymath4 Project is now underway, with the first formal post here. […]
Pingback by Michael Nielsen » Polymath4 — August 9, 2009 @ 10:34 pm |
Here’s another attempt to get some kind of adjustment argument going. Let’s suppose we have numbers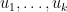 , all in the interval
, all in the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) (see comment 8), such that
(see comment 8), such that  . We now want to adjust the
. We now want to adjust the 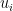 in order to decrease the error
in order to decrease the error  .
.
If we change each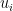 to
to 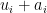 , then the product
, then the product 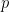 changes by a factor of
changes by a factor of 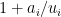 . Let
. Let  . Let the
. Let the 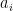 be a fairly randomish bunch of small numbers, some positive and some negative. Then the set of all possible distinct sums of the
be a fairly randomish bunch of small numbers, some positive and some negative. Then the set of all possible distinct sums of the 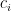 should be a fairly well-distributed set, because we would expect not just that the
should be a fairly well-distributed set, because we would expect not just that the 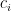 have very few linear relations, but also the stronger statement that it is difficult to approximate zero with small integer combinations of the
have very few linear relations, but also the stronger statement that it is difficult to approximate zero with small integer combinations of the 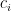 . And that kind of independence goes with good spanning properties. (We are trying to produce a number that’s close to
. And that kind of independence goes with good spanning properties. (We are trying to produce a number that’s close to 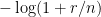 .)
.)
Comment by gowers — August 9, 2009 @ 10:53 pm |
A completely different thought, which is more like a question that I expect others to know the answer to. How well is approximated by
approximated by  ? Is the following approach hopeless?
? Is the following approach hopeless?
1. Work out and then raise it to the power
and then raise it to the power  .
.
2. Argue that is very close to
is very close to  , so
, so 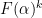 is very close to
is very close to  .
.
3. Observe that the inverse Fourier transform of is a convolution of a smooth function on an interval, and is therefore very nicely behaved. (Perhaps we could even put in weights to make
is a convolution of a smooth function on an interval, and is therefore very nicely behaved. (Perhaps we could even put in weights to make  a Gaussian so that convolution was particularly easy.)
a Gaussian so that convolution was particularly easy.)
4. Argue that the inverse Fourier transform of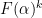 must approximate a smooth function in a sense that forces it to contain points in very small intervals.
must approximate a smooth function in a sense that forces it to contain points in very small intervals.
The dodgiest-looking step is 4. It seems that one would have to know far more accurately than is actually feasible if one wanted to get it to work. So what I’m asking is whether this pessimism is justified.
far more accurately than is actually feasible if one wanted to get it to work. So what I’m asking is whether this pessimism is justified.
Comment by gowers — August 9, 2009 @ 11:04 pm |
This sounds very much like Antal Balog’s approach from “On the distribution of integers having no large prime factors”, Journees Arithmetique Besancon, Asterisque 147/148 (1985), 27-31, except that he applied it to finding smooth numbers in short intervals, not non-smooth numbers — still, the approach is quite similar (instead of showing good uniform distribution results for log 2, …, log p_t, you just show good distribution for log p_s, …, log p_t — essentially the same problem). Basically, he showed that for near enough to 1/2 you can use the approximation you suggest, and then for
near enough to 1/2 you can use the approximation you suggest, and then for  somewhat larger, but still in the “critical strip”, one can use “average value” results of Montgomery et al, along with Holder’s inequality, to get good enough average-type bounds on
somewhat larger, but still in the “critical strip”, one can use “average value” results of Montgomery et al, along with Holder’s inequality, to get good enough average-type bounds on  . Combining all this together using the inverse-Mellin operator (as is used in the proof of PNT), he was able to show that intervals
. Combining all this together using the inverse-Mellin operator (as is used in the proof of PNT), he was able to show that intervals ![[n, n + n^{1/2+\epsilon}]](https://s0.wp.com/latex.php?latex=%5Bn%2C+n+%2B+n%5E%7B1%2F2%2B%5Cepsilon%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) contain
contain  -smooth integers. And probably you would get similar conclusions using your approach.
-smooth integers. And probably you would get similar conclusions using your approach.
By the way, these sorts of methods are often called “Dirichlet polynomial methods”, and your function is often called a “Dirichlet polynomial”.
is often called a “Dirichlet polynomial”.
Comment by Ernie Croot — August 9, 2009 @ 11:57 pm |
That sounds as though it answers an implicit question of mine, which is whether such methods can hope to break the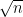 barrier. It would appear from what you say that they can’t.
barrier. It would appear from what you say that they can’t.
Comment by gowers — August 9, 2009 @ 11:59 pm |
Exactly. In fact, I vaguely recall that Friedlander et al once showed that even assuming RH one cannot break the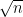 barrier (well, of course used in the most natural way — there may be other ways that produce stronger results). But maybe my memory is faulty.
barrier (well, of course used in the most natural way — there may be other ways that produce stronger results). But maybe my memory is faulty.
By the way, there was little typo in what I wrote above. In place of near to
near to  , I should have said that
, I should have said that 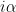 near to
near to  . Fixed now — Tim. PS If you write “latex” after your opening dollar signs then your LaTeX will come out as LaTeX. I’ve added it in for some of your comments.
. Fixed now — Tim. PS If you write “latex” after your opening dollar signs then your LaTeX will come out as LaTeX. I’ve added it in for some of your comments.
Comment by Ernie Croot — August 10, 2009 @ 12:50 am |
The general rule of thumb is that a discrete oscillatory sum can be efficiently approximated by its continuous counterpart iff its frequency is << 1 (cf. the Poisson summation formula). One can formalise this by a number of means, e.g. quadrature or the Euler integration identities, or by summation by parts.
The frequency of the phase is about
is about 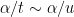 , so I would imagine that
, so I would imagine that  for
for 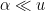 but not otherwise. For
but not otherwise. For 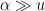 , the correct model is probably that of a random sum, so that
, the correct model is probably that of a random sum, so that  should be expected to have size about
should be expected to have size about  . Note that if one could actually formalise this intuition all the way, one would have solved the Lindehof hypothesis. Using van der Corput etc. one can at least get some power improvement
. Note that if one could actually formalise this intuition all the way, one would have solved the Lindehof hypothesis. Using van der Corput etc. one can at least get some power improvement  to the trivial bound O(u), which is where subconvexity bounds for zeta come from.
to the trivial bound O(u), which is where subconvexity bounds for zeta come from.
Comment by Terence Tao — August 10, 2009 @ 12:23 am |
[[ From Avi Wigderson ]]
I’m relaying here some comments and suggestions from Avi Wigderson. Note that there may be some inaccuracies in transcription; these are my fault, not Avi’s.
1. Complexity-theory approaches
Of course you know of Impagliazzo-W’97, and exponential circuit lower bounds for anything in DTIME(exp(n)), eg SAT, would suffice.
But the Prime-finding problem is a simpler derandomization problem – it is actually a unary problem (since if we want an n-bit prime we specify only log n bits).
So it seems like even uniform exponential lower bounds (on probabilistic algorithms, not circuits), in the sense of Impagliazzo-W’98 will do, namely will give a deterministic polytime alg for Prime-finding (well, there is ugliness, like the algorithm may only work for infinitely many n’s, etc).
BTW, IW98 deals only with “high-end” (exponential) lower bounds. One should be able to prove the following analogous “low-end” result.
Conjecture: If P != BPP then we get a deterministic algorithm for Prime-finding (indeed, for any problem in Promise-BPP) running in time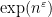 for all
for all  .
.
The above would be especially nice since also the assumption P=BPP should give something: not quite Prime-finding of course, being a search problem, but perhaps one can formulate a related problem which will benefit from this “win-win” situation.
2. Number-theoretic approaches
When AKS came out I thought the following “program” to Prime-finding might be good, but never followed up on it. Let me try to recollect it. . I think their characterization of primes is very relevant to the problem at hand. Lets recall it:
AKS characterization:
* For given integer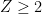 , let r be a positive integer less than Z, for which Z has order at least
, let r be a positive integer less than Z, for which Z has order at least  modulo r. Then Z is prime if and only if
modulo r. Then Z is prime if and only if
** Z is not a perfect power, ,
,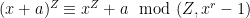 for each integer
for each integer  .
.
** Z does not have any prime factor
**
Note that the number r, which needs to have special properties, has only poly(n) possibilities for Z of n-bits, so we can try them all. Therefore I will assume that an appropriate r is given.
The AKS criterion is somewhat like the converse of Fermat’s little theorem (well, allowing Carmichael numbers…) , only that the condition is stated for poly(n) many a’s, each poly(n) small, (rather than exponentially many, exp large ones)! We’ll try to capture it by iterations of r-dimensional linear maps below, but I’ll build up to it.
In the following let me state stronger and stronger conjectures about iterates of modular linear maps. They will lead to a deterministic prime-finding algorithm – indeed to a proof of Cramer-like conjecture from which it would follow. Let me use the following notation.
Let P be a property (subset) of integers. Then we say that P is f(n) dense if every interval of length f(n) inside the n-bit integers has at least one member of P. For example, Cramer says that Primes are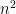 -dense.
-dense.
Conj 1: The solutions to are poly(n)-dense.
are poly(n)-dense.
This seems far weaker than Cramer – if not, this program is lost. Of course, I realize that algebraically it is a very strange condition, but still, primes satisfy it. Is there a way to prove that such solutions are dense on average without using primes? Here is the obvious generalization, replacing the constant 2 by any integer a. You’ll see the reason for the strange notation shortly. [NB: This is close to Strategy 4 – T.]
Conj 2: Let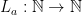 be the fixed linear map of the form
be the fixed linear map of the form  , with
, with  some integer. Then solutions to
some integer. Then solutions to 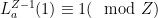 are poly(n,k)-dense.
are poly(n,k)-dense.
Now we’ll generalize it for a system of equations: all a < k:
Conj 3: Solutions to the system of k simultaneous equations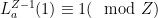 for all a<k are poly(n,k)-dense.
for all a<k are poly(n,k)-dense.
Now we’ll go up to dimension r, to capture the AKS condition (I’ll do it only for Z's which are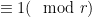 , but I hope it suffices, and anyway one can generalize what’s below for every Z). First, generalizing Conj 2 for a fixed
, but I hope it suffices, and anyway one can generalize what’s below for every Z). First, generalizing Conj 2 for a fixed  we have
we have
Conj 2’: Let as before. Let
as before. Let  be defined by the
be defined by the 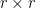 cyclic matrix A. It 1st column is
cyclic matrix A. It 1st column is  , and the others its cyclic shifts. Then solutions to
, and the others its cyclic shifts. Then solutions to
are poly(n,k,r)-dense.
And looking at systems of k equations, one for each we have the analog of Conj 3.
we have the analog of Conj 3.
Conj 3’: Let be as above (A=A(a)). Then solutions to the system
be as above (A=A(a)). Then solutions to the system
are poly(n,k,r)-dense.
Clearly, by the AKS theorem, Conj 3’ implies that primes are poly(n)-dense.
Comment by Terence Tao — August 9, 2009 @ 11:33 pm |
I think the best results toward conjectures 1 & 2 are those of Carl Pomerance:
C. Pomerance, On the distribution of pseudoprimes, Math. Comp. 37 (1981), 587-593.
C. Pomerance, A new lower bound for the pseudoprime counting function, Illinois J. Math. 26 (1982), 4-9.
C. Pomerance, Two methods in elementary analytic number theory, Number theory and applications, R. A. Mollin, ed., Kluwer Academic Publishers, Dordrecht, 1989, pp. 135-161.
(Which are available at http://math.dartmouth.edu/~carlp )
There is much too large a gap between these results. However, the conjectured density of pseudoprimes does support conjectures 1 & 2.
Many of the methods used by Pomerance seem to be applicable for conjecture 2′. I haven’t given any thought to simultaneous solutions as in conjectures 3 and 3′. In any case, there is lots of room for improvement in this area…
Comment by François Dorais — August 10, 2009 @ 5:59 am |
Can anything useful be done with quadratic sequences like the famous ? For small n this is often prime, but even for larger n it can be shown that each new number in the sequence either has
? For small n this is often prime, but even for larger n it can be shown that each new number in the sequence either has
(1) one new prime factor p that does not appear as a prime factor earlier in the sequence (in which case ), or
), or
(2) no new prime factors that do not appear earlier
The good news is that case (1) is very common, for it is about 87%. Can it be shown that for very large n we can find case (1) within a short enough subsequence to provide a
it is about 87%. Can it be shown that for very large n we can find case (1) within a short enough subsequence to provide a  quickly?
quickly?
WordPress doesn’t recognise \lte and \gte (and nor did I — are they macros of yours?) so I’ve changed them to \leq and \geq.
Comment by PhilGibbs — August 10, 2009 @ 7:32 am |
Can anything useful be done? Well, we can sort of do very useful things!. Assuming the Bateman-Horn conjecture, every polynomial f(n) without obvious obstructions to being prime infinitely often (i.e., f is irreducible, positive and there’s no “local” [that is, (mod q)] reason for it to not be prime) takes on prime values of n quite often. Actually, conditional on this conjecture, we can effectively get a O((10^k)^\epsilon) algorithm for any fixed \epsilon > 0 (although of course the implied constant goes to infinity as \epsilon goes to 0.) Unfortunately, Bateman-Horn seems way, way out of reach. (Wikipedia tells me that we don’t even have a single non-linear, one-variable polynomial that’s known to be prime infinitely often!)
Although the question you ask is slightly weaker, morally it’s probably almost as hard as Bateman-Horn for general polynomials. (I’m trying to think of other cases where I’ve seen it used that, often times, the set of prime factors of a set S behaves much like the primes in S — one is the Sylvester-sequence proof of the infinitude of primes, but this is really coarse. Am I confused and wrong about that heuristic? Maybe.) My point, though, is that we know very little about how general polynomials, even quadratics, behave in terms of primality.
Of course, n^2+n+41 is sort of special; however, the reasons that it’s special are both incredibly interesting and rather deep and technical. As far as I know (keeping in mind that I know very little about algebraic number theory) it may be within reach to show something nice in this or a related special case, but it would almost certainly require very specialized, abstruse techniques, plus more than one theoretical breakthrough.
Comment by Harrison — August 11, 2009 @ 7:59 am |
Yes, having looked at this further I can’t see how we can get a provable result. The quadratic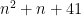 is special because it’s discriminant is 163 and it is the only reduced quadratic with that discriminant and
is special because it’s discriminant is 163 and it is the only reduced quadratic with that discriminant and ![Z[\sqrt{-163}]](https://s0.wp.com/latex.php?latex=Z%5B%5Csqrt%7B-163%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) has unique factorization.
has unique factorization.
Because of this we get a high proprtion of primes for small n, and the non-primes often have large factors, but for very large n I think there is not enough of a difference to be of use here.
For any polynomial P(n) you can construct a sieve to look for primes in P(n) because if prime p divides P(n) then it will divide some P(n) for some n, 0 <= n < p$. But I can’t see how that would help here.
An interesting question would be whether you could have a non-constant polynomial P(n) for which P(n) always has a prime factor greater than n. If you could prove that you had one it would solve the problem. I suppose it is not likely to be possible but it is surprising how long the sequences with this property can be for low degree polynomials. For you can go up to n=419 before all factors are less than n. For
you can go up to n=419 before all factors are less than n. For  it is up to 2390. For
it is up to 2390. For  it is 7755.
it is 7755.
Comment by PhilG — August 11, 2009 @ 11:49 am |
Let me check if I understand Gowers’s /approach and conjecture. (I am a little confused by the text around problem 3 in the main post):
Cramer conjecture that every interval [n,n+log^2n] contains a prime look hopeless (even if 2 is replaced by 10) and it is vey sensitive to the primes being exactly what they really are; so we try something weeker that does not rely so much on what the primes are. We look at the product of all integers in the interval [n,n+log^10n], (say) and ask: does it contain a large prime factor. Here large can mean “at least exp (k/log k)” where k = log n or perhaps just “at least exp (k^{1/10})”.
The hope is that 1) this is correct, 2) this does not depends on what the primes are really and will apply to “prime like” numbers (dense subsets of primes?) 3) additive combinatorics techniques can help. (Is this a correct description?)
Comment by Gil Kalai — August 10, 2009 @ 9:41 am |
Because the comments above seem to suggest that finding factors in an interval by anything like the kinds of counting methods used in analytic number theory (by which I mean the kinds of methods that might give not just one solution but an asymptotic for the number of solutions) appears to be known to be hard, I’m finding myself drawn to very elementary and explicit approaches. Here is a thought in that direction.
Suppose we are trying to approximate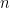 by a product of numbers that all belong to the interval
by a product of numbers that all belong to the interval ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) . In one or two earlier comments I’ve suggested getting reasonably close to
. In one or two earlier comments I’ve suggested getting reasonably close to 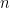 in a crude way and then refining things. In that vein, one would like to have ways of changing a product by an amount that one can control. In particular, one would like to be able to change it by a small amount.
in a crude way and then refining things. In that vein, one would like to have ways of changing a product by an amount that one can control. In particular, one would like to be able to change it by a small amount.
Here’s one trick for doing that. Assume that there’s some such that
such that 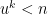 and
and  . Then find a number
. Then find a number  in
in ![[u,u+v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cu%2Bv%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that
such that 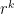 is close to
is close to  , which we can do with an error of about
, which we can do with an error of about  . Let’s assume that the error actually has that order of magnitude (rather than just being bounded above by that order of magnitude) and also that
. Let’s assume that the error actually has that order of magnitude (rather than just being bounded above by that order of magnitude) and also that 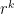 is slightly larger than
is slightly larger than 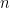 rather than slightly smaller. We can now replace
rather than slightly smaller. We can now replace 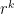 by
by 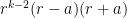 , and if we do so then we reduce the product by
, and if we do so then we reduce the product by  . If we choose
. If we choose  to be maximal such that the error is still positive, then we’ll have reduced it to something of order of magnitude
to be maximal such that the error is still positive, then we’ll have reduced it to something of order of magnitude  , where
, where  has order of magnitude
has order of magnitude  . In other words,
. In other words,  is around
is around  , so the new error is more like
, so the new error is more like 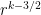 .
.
We can iterate this: at the next step we replace two more s by
s by  and
and  , reducing the error by something that equals
, reducing the error by something that equals  plus lower-order terms. Choosing
plus lower-order terms. Choosing 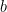 to be maximal such that the error is positive, we reduce the error to order of magnitude
to be maximal such that the error is positive, we reduce the error to order of magnitude  , where this time
, where this time  has order of magnitude
has order of magnitude 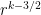 , so
, so 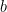 has order of magnitude
has order of magnitude 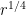 . So now the error is reduced to
. So now the error is reduced to  .
.
Continuing like this we could get to , but we want something a lot better than this.
, but we want something a lot better than this.
However, that was just the first stage. We were using there the fact that is very close to
is very close to 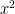 ,
,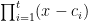 where the
where the 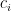 are small and the product equals
are small and the product equals  plus terms in
plus terms in 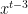 or lower. More generally, one would like better and better pairs of factorizable polynomials that approximate each other.
or lower. More generally, one would like better and better pairs of factorizable polynomials that approximate each other.
but we could go for better polynomial approximations. To improve on the above, one needs a product of the form
The more I write this, the more I start to have the depressing feeling that it’s not going to give good bounds at all. It seems to be too much effort just to make an improvement to the error of a factor of , which is very small compared with
, which is very small compared with 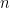 . Nevertheless, the more general idea of successive adjustments still seems to have some promise I think.
. Nevertheless, the more general idea of successive adjustments still seems to have some promise I think.
Comment by gowers — August 10, 2009 @ 9:41 am |
I don’t think you can eliminate even the term by choosing
by choosing  , since we know that the sum-of-squares of the roots of this polynomial is positive and equal to $d^2 – 2e$, unless I have made a foolish error.
, since we know that the sum-of-squares of the roots of this polynomial is positive and equal to $d^2 – 2e$, unless I have made a foolish error.
Not only that, but even producing two polynomials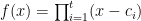 and
and 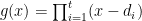 , where the
, where the  are integers, such that
are integers, such that  has degree lower than about
has degree lower than about  is a known hard problem, related to the Tarry-Escott Problem. Peter Borwein et al have some good papers on this (see e.g. the paper “The Prouhet-Tarry-Escott Problem revisited”, which can be downloaded from Peter’s very nice website).
is a known hard problem, related to the Tarry-Escott Problem. Peter Borwein et al have some good papers on this (see e.g. the paper “The Prouhet-Tarry-Escott Problem revisited”, which can be downloaded from Peter’s very nice website).
Also, I just want to point out that constructing polynomials with lots of linear factors as a means of producing smooth numbers in short intervals, and perhaps also non-smooths in short intervals, had been considered by Friedlander and Lagarias in their paper “On the distribution of short intervals of integers having no large prime factor”, J. of Number Theory 25 (1987), 249-273. As I recall (I can’t download the article just now, so can’t check what I am about to write) they work with polynomials such as your above where the
above where the 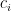 sum to
sum to  , and then they choose the
, and then they choose the 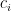 optimally to force short intervals to contain smooth numbers.
optimally to force short intervals to contain smooth numbers.
Comment by Ernie Croot — August 10, 2009 @ 5:06 pm |
Let me just make one more comment: if the polynomials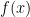 and
and 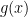 above are allowed to be of the form
above are allowed to be of the form  , where the
, where the 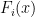 have degree at most $d$, and if $g(x)$ is allowed to have an analogous form, then one can get around the “Tarry-Escott problem” (or rather, one has a Tarry-Escott problem in a number ring that is easier to solve than in the integers), and can get
have degree at most $d$, and if $g(x)$ is allowed to have an analogous form, then one can get around the “Tarry-Escott problem” (or rather, one has a Tarry-Escott problem in a number ring that is easier to solve than in the integers), and can get  to have much lower degree than
to have much lower degree than 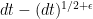 . Also, working with more variables can perhaps lead to more improvements.
. Also, working with more variables can perhaps lead to more improvements.
I once had the (perhaps naive and foolish) idea of trying to construct a sequence of polynomials, say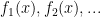 , such that
, such that  has “low degree”, so that upon substituting in
has “low degree”, so that upon substituting in  for some integer
for some integer  , one has a sequence of integers
, one has a sequence of integers  , each in sequence close to its predecessor, so that one gets every short interval has a highly smooth number, thereby improving upon Balog et al. Unfortunately, I wasn't able to get more than a bounded number of these polynomials in sequence.
, each in sequence close to its predecessor, so that one gets every short interval has a highly smooth number, thereby improving upon Balog et al. Unfortunately, I wasn't able to get more than a bounded number of these polynomials in sequence.
Comment by Ernie Croot — August 10, 2009 @ 5:21 pm |
Regarding “pseudoprimes”, namely numbers for which 2^n=2 modulo n. What is known about them? their density? the corresponding “L-function” etc?
(Also it will be nice to find a toy problem which is further away from the original problem.)
Comment by Gil Kalai — August 10, 2009 @ 9:52 am |
It is conjectured that the number of pseudoprimes to any base
of pseudoprimes to any base 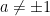 satisfies
satisfies
However, to the best of my knowledge, the best known bounds are
and
where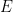 is a constant which is conjectured to equal
is a constant which is conjectured to equal  but is only known to have value at least
but is only known to have value at least  These results can be found in the references that I gave in my reply to #18. I would add that better bounds are known to hold on average, see:
These results can be found in the references that I gave in my reply to #18. I would add that better bounds are known to hold on average, see:
P. Erdős and C. Pomerance, On the number of false witnesses for a composite number, Math. Comp. 46 (1986), 259-279.
There is much room for improvement and new ideas here…
Comment by François Dorais — August 10, 2009 @ 1:52 pm |
The first Pomerance article that François Dorais mentions in thread 18 (which can be found here: http://math.dartmouth.edu/~carlp/PDF/paper32.pdf ) gives that the number of pseduoprimes (that is composite numbers satisfying ) less than
) less than  is big-
is big- of
of 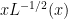 where
where 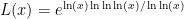 . They conjecture this can be improved to
. They conjecture this can be improved to  .
.
In the other direction Pomerance has shown (see: http://math.dartmouth.edu/~carlp/PDF/lower.pdf ) that the number of pseduoprimes is greater than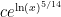 . In fact, the last bound is obtained by only counting pseduoprimes with more than
. In fact, the last bound is obtained by only counting pseduoprimes with more than  distinct prime factors.
distinct prime factors.
Comment by Mark Lewko — August 10, 2009 @ 2:08 pm |
Thanks! I realize that the term “pseudoprimes” means that the number is not a prime, and that it is conjectured but not known that there are much more pseudoprimes than primes.
Comment by Gil — August 11, 2009 @ 11:01 am |
In there paper “On gaps between squarefree numbers” Michael Filaseta and Ognian Trifonov establish the following theorem. There is a constant c such that for x sufficiently large the interval (x, x+c(x^3/14) contains a squarefree number. I have found the article here:
http://books.google.com/books?id=G02moOmuOX4C&pg=PA235&dq=squarefree+numbers#v=onepage&q=squarefree%20numbers&f=false
Part of the book
_Analytic number theory:
Proceedings of a conference in honor of Paul Bateman_
is online at google books and this article is there. Perhaps these methods could be used to improve the time it takes to find two consecutive square free integers from the current bounds?
Comment by Kristal Cantwell — August 10, 2009 @ 3:35 pm |
Granville (ABC Allows Us to Count Squarefrees) has improved this gap result to![[x,x+x^{\epsilon}]](https://s0.wp.com/latex.php?latex=%5Bx%2Cx%2Bx%5E%7B%5Cepsilon%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) for every
for every  conditional on the abc-conjecture. I don’t think it follows directly but, in light of this, it may be reasonable to pursue the “weak conjecture” under these assumptions. That is, find a deterministic
conditional on the abc-conjecture. I don’t think it follows directly but, in light of this, it may be reasonable to pursue the “weak conjecture” under these assumptions. That is, find a deterministic 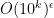 -step algorithm that finds consecutive
-step algorithm that finds consecutive  -digit square-free numbers conditional on square-free testing (or factoring) and the abc-conjecture.
-digit square-free numbers conditional on square-free testing (or factoring) and the abc-conjecture.
Comment by Mark Lewko — August 10, 2009 @ 7:51 pm |
It seems to me that the argument of Granville in “ABC Allows Us to Count Squarefrees” can actually be used to prove the following result. Assume the $abc$ conjecture and fix $\varepsilon>0$. Then for $x$ sufficiently large, the density of squarefree integers in $[x,x+x^{\varepsilon}]$ is $> \frac12$.
Here is the argument (see section 5 of Granville’s paper). Let us suppose that there exists arbitrarily large x such that the density is $\leq \frac12$. Using Eratosthenes’ sieve, there are approximately $\frac{6}{\pi^2} \cdot x^{\varepsilon}$ integers in the interval which are not divisible by the square of any prime $\leq x^{\epsilon}$. (In fact one can get a lower bound for this density which is as close of $\frac{6}{\pi^2}$ as one wishes, by taking large values of $x$.) Since $\frac{6}{\pi^2}>\frac12$, there must exists a positive density (say $\frac{1}{10}$) of integers in $[x,x+x^{\epsilon}]$ which are divisible by the square of some prime number $>x^{\varepsilon}$. This must also hold in some small interval of fixed length $k$ : there exists $m$ in $[x,x+epsilon]$ such that among $m+1, m+2, \ldots, m+k$, at least $\frac{1}{10}$ is divisible by $p^2$ for some $p>x^{\varepsilon}$. So $g(m)=(m+1)(m+2)\ldots(m+k)$ is divisible by $q^2$ for some $q>(x^{\epsilon})^{k/10} \geq m^{\varepsilon k/10}$. Take $k$ such that $\varepsilon k/10 > 1+\varepsilon$ (such a choice depends only on $\varepsilon$). Then we have a contradiction with Theorem 6 in Granville’s paper (which says that if $q^2$ divides $g(m)$ then $q \ll_{\varepsilon} m^{1+\varepsilon}$).
Please tell me whether the argument is correct, as I may over overlooked something.
Comment by François Brunault — August 11, 2009 @ 4:54 pm |
Later Filaseta and Trifonov improved their interval containing a squarefree to $(x – Cx^{1/5}\log(x),x]$ for some positive constant $C$. See
M. Filaseta and O. Trifonov, On gaps between squarefree numbers. II, J. London Math. Soc. (2), 45 (1992), no. 2, 215-221.
Comment by Anon — August 10, 2009 @ 8:54 pm |
Random experiment: Sylvester’s sequence can be modified with different “seeds”.
For example, one can define
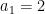


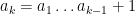 for all subsequent k.
for all subsequent k.
and
getting the sequence
2, 3, 5, 31, 931, 865831, 749662454730, …
(not in the OEIS)
however 749662454730 is not square-free.
Comment by Jason Dyer — August 10, 2009 @ 6:29 pm |
Erk, I meant 749662454731 which *is* square-free.
Comment by Jason Dyer — August 10, 2009 @ 6:42 pm |
Based on some further experiments–
Conjecture: If the initial p values in a sequence are the first p consecutive primes as in the example above, and for all subsequent k, all terms in the sequence are square-free.
for all subsequent k, all terms in the sequence are square-free.
Even if untrue I think a counterexample would be illuminating.
It might be better in considering the problem to use only one initial value and allow it to be a square-free composite (starting with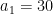 for example would yield the same continuation of sequence as starting with
for example would yield the same continuation of sequence as starting with 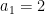 ,
, 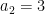 ,
,  ).
).
Comment by Jason Dyer — August 11, 2009 @ 12:16 am |
Hmm, assuming you mean a_k = a_1…a_k + 1, then the conjecture for composite initial value (excluding the trivial case when a_1+1 isn’t squarefree) is obviously equivalent to the following: If r, r+1 are squarefree, then so is r^2+r+1, which seems a little strong. (And in fact checking the first few cases gives a counterexample with r = 22, since 22*23 + 1 = 507 = 3*169.)
I’m also not entirely convinced in the case of starting with small primes; certainly I can’t think of a heuristic argument in support. Do you have one, or is this just based on numerical evidence?
Comment by Harrison — August 11, 2009 @ 7:00 am |
22 doesn’t fall into the conjecture, the only composites that do are
2 * 3
2 * 3 * 5
2 * 3 * 5 * 7
2 * 3 * 5 * 7 * 11
etc.
This is purely numerical, I don’t even know why the original conjecture would be true. The reason I tried this though was knowing that the original sequence tried to ape Euclid’s proof of the infinitude of the primes somewhat, and seeing what would happen if we began the sequence at essentially a different point of the proof.
Comment by Jason Dyer — August 11, 2009 @ 1:07 pm |
Ah, okay; I thought you meant a general squarefree composite as the starting point, which was clearly too strong.
Still, though, the fact that that is too strong means that obviously you need to use something like the smoothness of that sequence (6, 30, 210, 2310…) to have any hope of proving it or even providing compelling evidence for it, and the only reason I can think of that that would help to prevent repeated prime factors is that it obviously prevents small enough repeated prime factors in the modified Sylvester sequence, and just knocking out the small prime factors isn’t in general going to be good enough. Actually, I’ll bet that the extended conjecture that these Sylvester-like sequences are squarefree is false; if I’m convinced otherwise, I’ll perform a song about the simplex algorithm set to Missy Elliott and put it on YouTube. (Who am I kidding? I’d do that anyway.)
Comment by Harrison — August 11, 2009 @ 8:42 pm |
After playing around in Wolfram Alpha for a half hour, I see that the numerical evidence is pretty strong, but I’m not ready to concede.
In the more general situation when r, r+1 are squarefree, I also have some numerical evidence that backs up my intuition that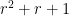 is reasonably frequently squareful; on the basis of Mathematica calculations (specifically, Count[Table[4*MoebiusMu[n]^2+2*MoebiusMu[n+1]^2+MoebiusMu[n^2+n+1]^2, {n, 1, 1000}], 6] , and we replace the upper limit by steadily bigger numbers) it looks like about 2% of all integers have the property that both
is reasonably frequently squareful; on the basis of Mathematica calculations (specifically, Count[Table[4*MoebiusMu[n]^2+2*MoebiusMu[n+1]^2+MoebiusMu[n^2+n+1]^2, {n, 1, 1000}], 6] , and we replace the upper limit by steadily bigger numbers) it looks like about 2% of all integers have the property that both  are squarefree, but
are squarefree, but  is not. Which means that if I can check, oh, 60 or 70 terms in the various Sylvester-type series and don’t find anything, I’ll start to believe the squarefreeness conjecture, but barring that (or a good heuristic argument) I’m unconvinced.
is not. Which means that if I can check, oh, 60 or 70 terms in the various Sylvester-type series and don’t find anything, I’ll start to believe the squarefreeness conjecture, but barring that (or a good heuristic argument) I’m unconvinced.
Comment by Harrison — August 11, 2009 @ 9:35 pm |
Here’s a stronger restatement of the conjecture, although I still don’t have any confidence the original version is true. This is based purely on numerical evidence.
Conjecture: Let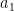 be a positive integer and
be a positive integer and  for all subsequent k.
for all subsequent k.
If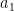 or
or 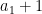 is a primorial number, the sequence is square-free. Otherwise, the sequence is squareful.
is a primorial number, the sequence is square-free. Otherwise, the sequence is squareful.
Comment by Jason Dyer — August 12, 2009 @ 1:27 pm |
There’s an Erdos paper titled “On the Converse of Fermat’s Theorem” (I put a link on the wiki). I haven’t tracked down the reference, but in it he writes: “Sierpinski gave a very simple proof that there are infinitely many pseudoprimes, by proving that if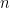 is a pseudoprime then
is a pseudoprime then 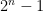 is also a pseudoprime.” Unless I’m mistaken, shouldn’t this give a polynomial time pseudoprime construction (answering the question Noam raised in thread 29 on the previous post)? The Erdos paper itself is interesting, establishing that there exists infinitely many square-free pseudoprimes with a fixed number of prime factors.
is also a pseudoprime.” Unless I’m mistaken, shouldn’t this give a polynomial time pseudoprime construction (answering the question Noam raised in thread 29 on the previous post)? The Erdos paper itself is interesting, establishing that there exists infinitely many square-free pseudoprimes with a fixed number of prime factors.
Comment by Mark Lewko — August 11, 2009 @ 7:40 am |
Ooh, that’s a nice observation, and does technically solve Noam’s problem (though not Avi’s Conj 1 at #18). The proof that 2^n-1 is a pseudoprime is cute: 2^n equals 1 mod 2^n-1, and (2^n-1)-1 is a multiple of n, hence 2^{(2^n-1)-1} equals 1 mod 2^n-1.
Now if we can get a much denser set of pseudoprimes than this, then we might be getting somewhere… the next thing to try, perhaps, is numbers of the form k \times 2^n – 1,/math> where n is pseudoprime (or prime)? (We’d also like to simultaneously be a pseudoprime with respect to both 2 and 3 (say), but this looks trickier).
Comment by Terence Tao — August 12, 2009 @ 3:51 pm |
There is another construction of pseudoprimes (Cipolla, 1904). Let be the
be the  -th Fermat number. Note that
-th Fermat number. Note that 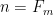 satisfies
satisfies 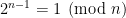 . Now take any sequence of integers
. Now take any sequence of integers 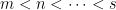 (at least two terms). Then the product
(at least two terms). Then the product 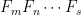 is a pseudoprime if and only if
is a pseudoprime if and only if 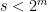 . There is also a natural generalization for pseudoprimes to any base a.
. There is also a natural generalization for pseudoprimes to any base a.
I'm not sure whether this gives a denser set of pseudoprimes, though.
Comment by François Brunault — August 13, 2009 @ 4:15 pm |
This is a rather silly approach for many many reasons, and I don’t expect anything to come of it, but maybe it’s instructive nonetheless. There is of course already a “deterministic” way to find large primes (those scare-quotes are necessary!!), which is by using Mills’ constant. The scare quotes, of course, are there because no one seriously believes that there’s a way to compute Mills’ constant apart from finding an actual, appropriate sequence of primes. (It’s worth noting, however, that with an oracle that provided the nth bit of Mills’ constant I think we’d be done. It’s just that this oracle is so ridiculous that we might as well assume an oracle that makes the problem trivial, like one that picks an n-bit prime for each n and when fed an n-bit number tells you whether you’re too high or too low.)
But I don’t want to talk about Mills’ constant per se; rather, I want to talk about the sequence a_i used to define them, which is recursively constructed by taking a_{n+1} to be the smallest prime less than a_n^3. There are two salient points here:
1. The reason Mills’ constant exists is that it’s known that there’s a prime between large enough consecutive cubes. Maybe this is the sleep deprivation talking (I’m writing this at 4 AM local time), but the fact that this is known and the analogous problem for squares is wide open seems to perhaps be related to Terry’s comment way back in comment 3 about how K+K is usually well-behaved, but K+K+K is always well-behaved. If so, I find it striking that a result of that nature has already led to a *cough* “deterministic” *cough* algorithm for finding primes.
2. Note that the gaps between a_i^3 and the next prime are pretty tiny — on the order of log n, which admittedly isn’t that significant considering the sample size and the fact that (assuming RH? I know assuming the Cramer model, but I think you can use something weaker — does the PNT work straight-up? Again, I apologize for the sleep deficit. Though it is your fault, polymath. :) ) most prime gaps are that big. But maybe there’s something we can take advantage of in the structure of the problem to show that the gaps really are that small in this case, or to otherwise find a prime between the cubes in polynomial time. This is an incredibly long shot, but one advantage of polymath is that there’s nothing to lose by attempting Hail Marys. (I just mixed American football and naval metaphors, yes. Sorry again.) If we could manage that, we’d have a full solution to the strong conjecture assuming RH, so it’s at least worth giving a second thought, IMO.
Comment by Harrison — August 11, 2009 @ 8:34 am |
A tiny point — the sequence as you’ve defined it is 2,2,2,… but you clearly meant “largest” when you wrote “smallest” in the second paragraph.
I’m not sure that the thing about cubes is analogous to the K+K versus K+K+K thing. If you assume RH then it follows that the distance between successive primes cannot be more than about , and that’s the best you can hope to prove by that kind of method I think. But using sieves they have got unconditional results, and I’m guessing from what you say that they can prove
, and that’s the best you can hope to prove by that kind of method I think. But using sieves they have got unconditional results, and I’m guessing from what you say that they can prove  for some
for some 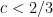 , which then implies the statement about consecutive cubes. Somehow this doesn’t really connect with threefold sumsets, unless I’ve missed something.
, which then implies the statement about consecutive cubes. Somehow this doesn’t really connect with threefold sumsets, unless I’ve missed something.
Comment by gowers — August 11, 2009 @ 9:57 am |
Actually, I meant “greater” when I wrote “less,” although I suppose it doesn’t actually matter.
I know…nothing about how sieve theory connects with analytic number theory, but the main result that Mills used relates the exponent in the prime gap to the growth rate of the Riemann zeta function on the critical line. In particular, that method gave you an exponent of at most 5/8, so you could really replace the 3 in Mills’ theorem with anything at least 8/5. So, yeah, it does appear that I read too much into the 2 vs. 3 thing.
One thing I didn’t mention the first time around is that this is a further example of the fact that double-exponential sequences are, for some reason, relatively easy to control with regard to primality. Actually, you have a ridiculous amount of control; for instance, by precisely the same arguments as with Mills’ theorem, there’s some constant A for which![[A^{3^n}]](https://s0.wp.com/latex.php?latex=%5BA%5E%7B3%5En%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) is prime iff the nth bit in the binary expansion of
is prime iff the nth bit in the binary expansion of  is 1. (Exercise: Find some similarly ridiculous degree of freedom relating to the Sylvester and Fermat sequences.) I’m probably still not entirely lucid, but that seems encouraging, since when we have that much control over something it often means that we can improve some bound somewhere, by arbitrage or another trick.
is 1. (Exercise: Find some similarly ridiculous degree of freedom relating to the Sylvester and Fermat sequences.) I’m probably still not entirely lucid, but that seems encouraging, since when we have that much control over something it often means that we can improve some bound somewhere, by arbitrage or another trick.
Comment by Harrison — August 11, 2009 @ 10:26 am |
I discussed a bit the Mills constant recently (see here; the information it uses about primes is really that there there exists a constant strictly less than 1 such that intervals
strictly less than 1 such that intervals  always contain a prime. This type of fact is more or less implied by saying that there is no zero of the Riemann zeta function with real part larger than
always contain a prime. This type of fact is more or less implied by saying that there is no zero of the Riemann zeta function with real part larger than  (which is not known yet), except that it is proved unconditionally by means of various tools to work around the Riemann Hypothesis.
(which is not known yet), except that it is proved unconditionally by means of various tools to work around the Riemann Hypothesis.
Comment by Emmanuel Kowalski — August 11, 2009 @ 12:54 pm |
Here is another possible approach, which is different from those already described. It’s also a long shot, of course.
From the analytic theory of the zeta function we know how to write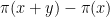 as a main term, plus a sum over zeros of
as a main term, plus a sum over zeros of 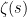 . When
. When 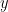 is small, of course, it becomes much harder to control this second term. However, one might try the following: given a large
is small, of course, it becomes much harder to control this second term. However, one might try the following: given a large  , assuming that there is no prime in various intervals of length
, assuming that there is no prime in various intervals of length  (where
(where  is fixed) located near
is fixed) located near  (between
(between  and
and 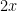 , say), we will get some relations between zeros of
, say), we will get some relations between zeros of 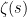 . We can’t really hope to get a contradiction from there, but maybe one could use those relations (we can afford also a power of $\log x$ of them) to pinpoint another interval of similar length, still located around
. We can’t really hope to get a contradiction from there, but maybe one could use those relations (we can afford also a power of $\log x$ of them) to pinpoint another interval of similar length, still located around  , where the corresponding sum over the zeros goes in the right direction to ensure the existence of a prime.
, where the corresponding sum over the zeros goes in the right direction to ensure the existence of a prime.
This is at least somewhat realistic since we know that there is, indeed, some prime of size around .
.
(This is vaguely motivated by the famous heuristic argument of Hadamard to show that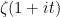 is never zero: if
is never zero: if 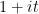 was such a zero, playing with the logarithmic derivative leads to “guess” that
was such a zero, playing with the logarithmic derivative leads to “guess” that  would be a pole of zeta, which is not possible).
would be a pole of zeta, which is not possible).
Comment by Emmanuel Kowalski — August 11, 2009 @ 2:53 pm |
Are you looking for a theoretical proof that there are primes in a gap of order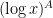 , or are you proposing that we numerically calculate
, or are you proposing that we numerically calculate  using the sum over zeta zeros?
using the sum over zeta zeros?
Has anyone checked the order of calculation required to find even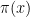 using the zeta function formula? I know it would be messy but if it can be done in polynomial time it is still a solution. Apologies if this was already ruled out, I couldn’t see it.
using the zeta function formula? I know it would be messy but if it can be done in polynomial time it is still a solution. Apologies if this was already ruled out, I couldn’t see it.
Comment by PhilG — August 11, 2009 @ 5:20 pm |
Here is an idea for how to construct a pair of square-free numbers that are very close together (hopefully polylog closeness or better), adapted from an idea of Lagarias and Odlyzko: way back in the 1980’s I think it was, L-O found a way to use the LLL algorithm to solve certain instances of the knapsack problem relevant to cryptosystems, such as Merkle’s knapsack method. The idea was that if one is presented with a collection of integers and a target
and a target 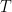 , then in certain situations one can often quickly locate a subset of the
, then in certain situations one can often quickly locate a subset of the  ‘s that sums to
‘s that sums to 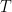 . How? Well, one builds a certain lattice, applies the LLL algorithm to find a short vector in it, which turns out to often be a scalar multiple of a certain 0-1 vector relative to the lattice basis vectors (at least if the set
. How? Well, one builds a certain lattice, applies the LLL algorithm to find a short vector in it, which turns out to often be a scalar multiple of a certain 0-1 vector relative to the lattice basis vectors (at least if the set 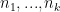 satisfies the right sort of `density requirements’, which often hold when the
satisfies the right sort of `density requirements’, which often hold when the  have many digits relative to
have many digits relative to  ), and then this 0-1 vector corresponds to the subset summing to
), and then this 0-1 vector corresponds to the subset summing to 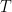 .
.
Using this idea, consider the lattice generated by the vectors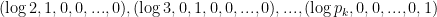 . Call this basis
. Call this basis 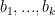 . This lattice does not have full rank, so LLL does not directly apply, but presumably this can be fixed somehow (e.g. using projections or some other trick). What would it mean to have an integer linear combination
. This lattice does not have full rank, so LLL does not directly apply, but presumably this can be fixed somehow (e.g. using projections or some other trick). What would it mean to have an integer linear combination  (i.e. a lattice point) of small Euclidean norm? It would mean that one has an integer linear combination of the
(i.e. a lattice point) of small Euclidean norm? It would mean that one has an integer linear combination of the  that comes close to
that comes close to  (look at the first coordinate), where the coefficients themselves cannot be too big (because the second through
(look at the first coordinate), where the coefficients themselves cannot be too big (because the second through  th coordinates of the linear combination give you the
th coordinates of the linear combination give you the 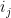 ‘s). Segregating the
‘s). Segregating the  ‘s that are positive from those that are negative, and then exponentiating, one gets two products of small primes that come very close to one another.
‘s that are positive from those that are negative, and then exponentiating, one gets two products of small primes that come very close to one another.
Now some of these powers can exceed 1, making the products not square-free, and this is where another idea of L-O comes in: for certain lattices the LLL algorithm often produces a lattice point that is a scalar multiple of the shortest non-zero lattice point, and if this is true in our case it means that the two products we get are actually th powers of square-free numbers, for some
th powers of square-free numbers, for some  (so, taking
(so, taking  th roots, we are done).
th roots, we are done).
I suspect that with the lattice approach I just described what will happen is that because there are so many potential small linear combinations (think about how many consecutive smooth, square-free pairs of integers one can create), the algorithm will not work (for a complicated set of reasons); but, there might be ways to refine it through finding more than one short vector (again, for a complicated set of reasons), since LLL actually returns a short basis, not just a single short vector. Also, there is the issue that the coefficients might turn out to be too small, leading to only very small pairs that are square-free numbers, but I don’t think this is a problem because in the end such combinations don’t correspond to super-small lattice vectors.
Comment by Ernie Croot — August 11, 2009 @ 4:26 pm |
Let me add that one should weight the first coordinates of the lattice vectors a little differently, which is standard in lattice basis reduction applications. So, the basis should perhaps be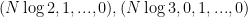 and so on, for a carefully chosen
and so on, for a carefully chosen  .
.
Comment by Ernie Croot — August 11, 2009 @ 5:36 pm |
Assume the following two statements:
1. For every sufficiently large N, there are roughly the expected number of primes between N and N^(1+\epsilon(N)), where \epsilon(N)->0 as N->infty.
2. We have a “constructive” upper-bound sieve – i.e., not just a nice function f that majorises the primes
in an interval, and does so fairly tightly, but also an algorithm that gives us quickly a random integer
n for which f(n) is >=1 or >=0.5 or what have you.
Here assumption 1 is a universally believed but very difficult conjecture (though much less strong than Cramer’s). It’s not immediately obvious to me whether 1 would be very hard or not in the case of Toy Problem 5.
Assumption 2 is an interesting problem that may be doable.
Now – we can clearly assume that epsilon(N) goes to 0 quite slowly as N->infty. Let us use a “constructive” upper bound sieve with support on {1,2,…,N^{epsilon(N)/2}}. Given an interval of length N^{epsilon(N)}, it will give us random elements of that interval that have a probability roughly equal to 1/epsilon(N) of being prime. If I understand correctly, this would solve the “weak” (not “very weak”) form of the problem.
Comment by Harald Helfgott — August 11, 2009 @ 4:42 pm |
Well, if we knew that every interval of the form![[N, N+N^\varepsilon]](https://s0.wp.com/latex.php?latex=%5BN%2C+N%2BN%5E%5Cvarepsilon%5D&bg=ffffff&fg=000000&s=0&c=20201002) contained a prime, we’d have an
contained a prime, we’d have an  algorithm immediately. RH implies that most intervals of this form contain a prime, but unfortunately in worst case we only get a gap of about
algorithm immediately. RH implies that most intervals of this form contain a prime, but unfortunately in worst case we only get a gap of about 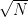 , which seems to be a fundamental barrier here.
, which seems to be a fundamental barrier here.
Generating an almost prime (which is basically what I would expect a decent majorant of the primes to be concentrated on) does indeed look like a viable toy problem, and is close to what is being aimed for in other approaches. With a factoring algorithm, of course, once one has a large almost prime, one also has a large prime.
Comment by Terence Tao — August 12, 2009 @ 3:18 pm |
Maybe the following is a related toy problem: consider sequence a_i described by a linear feedback shift register with period 2^m (and suppose m>>k). find an index between 2^k and 2^{k+1} where the value is ‘1’.
…This is not good since among every m consecutive elements we have a ‘1’ ; (and also the k is a complete red Herring). I suppose we need to ask a somehat more difficult question for LFSR (two consecutive ‘1’s?) or consider slightly more general pseudo random generators
Comment by Gil — August 11, 2009 @ 4:55 pm |
Let me a bit more abstract and remove all references to sieves.
Say that we can come up with a quick procedure to generate random integers of size about N having a positive probability (>= 1/10, say) of being prime. What would follow?
(Notes:
(1) In the case of toy problem 5, this is trivial – a random integer n of size about N has a positive probability of satisfying “n is squarefree and n+1 is squarefree”.
(2) What if the said random integers having a positive probablity of being prime were in a fairly short interval around N?)
Comment by Harald Helfgott — August 11, 2009 @ 8:13 pm |
On second thought – the said “quick procedure” is very easy to find. Just test log N random integers of size about N for primality – you’ll find a prime of size about N with probability >=0.5 in time polynomial on log N.
Comment by Harald Helfgott — August 11, 2009 @ 8:54 pm |
A comment on the Oracle Counterexample page of the polymath wiki. At the end it asks whether there is an oracle relative to which P=BPP but there is an efficiently recognizable dense set of integers (which we shall call “pseudoprimes”) for which polynomial time deterministic construction is impossible.
A relevant reference is paper of Fortnow in which it is noted in passing (page 3) that there are oracles in the literature that separate what he calls “Assumption 4” and “Assumption 3”. Assumption 4 is that P=BPP while Assumption 3 is a bit stronger than the assumption that any set of pseudoprimes has a deterministic construction. The difference has get to do with what Avi calls “unary inputs” in his post above; basically, in Assumption 3 we want to be able to construct elements from any set of “pseudoprimes” which is recognized by a *family of polynomial size circuits* while in the problem posed in the wiki we want to be able to construct elements from any set which is recognized by a *uniform polynomial time algorithm*; let us call it the Wiki Assumption
In any case, the same oracle mentioned by Fortnow should also falsify the Wiki Assumption, while having P=BPP.
The wiki page also raises the question of finding an oracle relative to which P!=BPP and the Wiki Assumption is false. In any oracle world in which P!=BPP, then Fortnow’s Assumption 3 is also false, and as discussed above Assumption 3 and the Wiki Assumption are very close. It is plausible that the standard oracle relative to which P!=BPP (which I am not familiar with) is also such that the Wiki Assumption fails, so it might be worth checking it out.
Comment by luca — August 11, 2009 @ 11:24 pm |
The standard construction of an oracle where P != BPP is very similar to the standard construction of an oracle where P != NP as described in the textbooks. If the oracle is A, the separating language L(A) is still the set of all unary inputs 1^n for which there exists a string of length n in A. But now, when you build A to diagonalize against the i-th polynomial-time machine, you make sure to include not *one or none* of the strings of a certain length but *many or none* of the strings of that length (that is, a constant fraction of all strings of that length, or none). This puts L(A) in BPP^A (in fact in RP^A). Note that it is always possible to add a constant fraction of the strings when required because a polynomial-time algorithm can only query a tiny fraction of all strings of the length of input.
The tricky part is in checking that, under this oracle, Assumption 3 is falsified and possibly also the Wiki assumption is falsified. The proof that P != BPP implies that Assumption 3 is falsified is not completely straightforward as far as I can see. We can try to look at it.
The natural path to show that P != BPP implies that Assumption 3 is falsified would be showing that if we can deterministically in polynomial time find an accepted input to circuits that accept many inputs, then we can approximate the acceptance probability of a given circuit in polynomial time. I would guess this is done by applying the assumed algorithm to the circuit that interprets its input as a sample of a few inputs to the given circuit for which we want to approximate its acceptance probability and checks if the fraction of accepted inputs is bigger than a threshold. The assumed algorithm will return a candidate sample, which we can check for correctness, and start over with a larger or smaller threshold depending on whether the candidate was wrong or right. Proceeding this way in binary search we should be able to approximate the acceptance probability of the given circuit.
And at this point I do not see why this shouldn’t work equally well with uniform algorithms, but I’ll pause here to be able to think about it.
Comment by Albert Atserias — August 12, 2009 @ 1:08 pm |
The “natural path” to show that Assumption 3 implies P = BPP suggested above can be made to work but it requires a bit more than what I sketched. This is actually done in Fortnow’s paper (see the proof of Theorem 2.7 in page 3). In turn, this “bit more” that is required seems to use circuits in an essential way (for example, in Fortnow’s proof, in the simulation of Lauteman’s promise-BPP in RP^{promise-RP}), in a way that seems to make the Wiki assumption insufficient to put L(A) in P^A (which would be the desired contradiction). In conclusion, it seems we need a refined oracle construction or a different argument linking Assumption 3 with P = BPP.
Comment by Albert Atserias — August 12, 2009 @ 3:56 pm |
Let me build on Emmanuel Kowalski’s excellent idea in comment number 28: we have a result which says that if RH holds then we can locate primes of size in time roughly
in time roughly  or so. Now, perhaps instead of trying to prove that intervals like
or so. Now, perhaps instead of trying to prove that intervals like ![[x, x + (\log x)^A]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x+%2B+%28%5Clog+x%29%5EA%5D&bg=ffffff&fg=000000&s=0&c=20201002) contain primes unconditionally, as Emmanuel suggested, we should first try to be much less ambitious and aim to show that *some* interval
contain primes unconditionally, as Emmanuel suggested, we should first try to be much less ambitious and aim to show that *some* interval ![[y, y + \sqrt{x}]](https://s0.wp.com/latex.php?latex=%5By%2C+y+%2B+%5Csqrt%7Bx%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) with
with ![y \in [x,2x]](https://s0.wp.com/latex.php?latex=y+%5Cin+%5Bx%2C2x%5D&bg=ffffff&fg=000000&s=0&c=20201002) , contains a prime number that we can discover computationally.
, contains a prime number that we can discover computationally.
How? Well, let’s start by assuming that we can computationally locate all the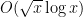 zeros in the critical strip up to height
zeros in the critical strip up to height  . Then what we can do is some kind of “binary search” to locate an interval
. Then what we can do is some kind of “binary search” to locate an interval ![[y, y + \sqrt{x}]](https://s0.wp.com/latex.php?latex=%5By%2C+y+%2B+%5Csqrt%7Bx%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) containing loads of primes: say at the ith step in the iteration we have that some interval
containing loads of primes: say at the ith step in the iteration we have that some interval ![[u,v]](https://s0.wp.com/latex.php?latex=%5Bu%2Cv%5D&bg=ffffff&fg=000000&s=0&c=20201002) has loads of primes. Then, using the explicit formula for
has loads of primes. Then, using the explicit formula for 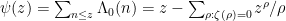 (actually, the usual quantitative form of the identity), we can decide which of the two intervals
(actually, the usual quantitative form of the identity), we can decide which of the two intervals ![[u, (u+v)/2]](https://s0.wp.com/latex.php?latex=%5Bu%2C+%28u%2Bv%29%2F2%5D&bg=ffffff&fg=000000&s=0&c=20201002) or
or ![[(u+v)/2, v]](https://s0.wp.com/latex.php?latex=%5B%28u%2Bv%29%2F2%2C+v%5D&bg=ffffff&fg=000000&s=0&c=20201002) contains loads of primes (maybe both do — if so, pick either one for the next step in the iteration). We keep iterating like this until we have an interval of width around
contains loads of primes (maybe both do — if so, pick either one for the next step in the iteration). We keep iterating like this until we have an interval of width around  or so that we know contains primes.
or so that we know contains primes.
Ok, but how do you locate the zeros of the zeta function up to height ? Well, I’m not sure, but maybe one can try something like the following: if we can understand the value of
? Well, I’m not sure, but maybe one can try something like the following: if we can understand the value of 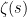 for enough well-spaced, but close together, points up the half-line, then by taking local interpolations with these points, we can locate the zeros to good precision. And then to evaluate
for enough well-spaced, but close together, points up the half-line, then by taking local interpolations with these points, we can locate the zeros to good precision. And then to evaluate  at these well-spaced points, maybe we can use a Dirichlet polynomial approximations, and then perhaps apply some variant of Fast Fourier Transforms (if this is even possible with Dirichlet polynomials, which are not really polynomials) to evaluate them at lots of values
at these well-spaced points, maybe we can use a Dirichlet polynomial approximations, and then perhaps apply some variant of Fast Fourier Transforms (if this is even possible with Dirichlet polynomials, which are not really polynomials) to evaluate them at lots of values 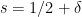 quickly — perhaps FFTs can speed things up enough so that the whole process doesn’t take more than, say,
quickly — perhaps FFTs can speed things up enough so that the whole process doesn’t take more than, say, 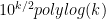 bit operations. Keep in mind also that our Dirichlet polynomial approximation only needs to hold “on average” once we are sufficiently high up the half-line, so it seems quite plausible that this could work (and for
bit operations. Keep in mind also that our Dirichlet polynomial approximation only needs to hold “on average” once we are sufficiently high up the half-line, so it seems quite plausible that this could work (and for  near to
near to  we would need to be more careful, and get the sharpest approximation we can, because those terms contribute more in the explicit formula).
we would need to be more careful, and get the sharpest approximation we can, because those terms contribute more in the explicit formula).
I realize that there are far better methods than what I describe for locating zeros of the zeta function, and in the end it might be better to use one of these other methods, assuming what I write above can work.
Comment by Ernie Croot — August 12, 2009 @ 12:56 am |
So, I’m a little confused. We’re trying here to find a good y with a prime in![[y, y+\sqrt{x}]](https://s0.wp.com/latex.php?latex=%5By%2C+y%2B%5Csqrt%7Bx%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) ? Or are we actually trying to compute the prime? (I guess in the computational range of
? Or are we actually trying to compute the prime? (I guess in the computational range of  , it doesn’t really matter, and I assume that that’s the broken formula, but I can’t actually tell.) I guess I’m just unsure about whether “that we can discover computationally” is modifying “prime” or “interval.”
, it doesn’t really matter, and I assume that that’s the broken formula, but I can’t actually tell.) I guess I’m just unsure about whether “that we can discover computationally” is modifying “prime” or “interval.”
Comment by Harrison — August 12, 2009 @ 2:49 am |
It is modifying “prime”. The problem with the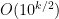 algorithm is that it assumes RH — without RH we get something a little worse, like
algorithm is that it assumes RH — without RH we get something a little worse, like  running time.
running time.
All I am saying is that we don’t really need that RH even holds (assuming, of course, that the zeros can be computed quickly); in fact, there can even be zeros off the half-line, and the approach will work. It’s enough to be able to compute all the zeros of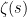 in the critical strip up to height about
in the critical strip up to height about  . Once one has these zeros to enough precision, one can just do a binary search to locate an interval of width
. Once one has these zeros to enough precision, one can just do a binary search to locate an interval of width  , and all elements greater than
, and all elements greater than  , that contains a prime. Once one has the endpoints of said interval, one just tests the numbers in it one-by-one (using AKS) until a prime is found.
, that contains a prime. Once one has the endpoints of said interval, one just tests the numbers in it one-by-one (using AKS) until a prime is found.
I should also say that the idea I have stated is a little different than Emmauel’s. Emmanuel starts with intervals having no primes, and then tries to force relations on zeros. My approach starts with the zeros, and then tries to locate the interval.
Comment by Ernie Croot — August 12, 2009 @ 3:00 am |
Sorry if I am repeating something that was already said; I do not see now how a factoring oracle is going to help. Under the Cramer model since every n digits integer is a prime with probability 1/n or so every interval of size n^10 contains a prime so we can look one by one there and trace it.
If we replace “primes” by “integers having prime factors of at least n^{1/3} digits then the probability 1/n is changes into 1-t where t is very very very tiny. So we can be much more certain in our hearts that every interval of length n^10 will contain such a guy. Yet to spoil this we still need to eliminate a very small number of primes; so I do not see how the additive number theory approach can go around it. Namely, I do not see how the logs of all primes are different than the logs of all primes after eliminating those we want to.
Comment by Gil Kalai — August 12, 2009 @ 6:29 am |
As I mentioned in comment 28 there may be a solution to this problem based on numerical calculation of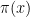 using Riemann’s analytic formula using a sum over the zeros of the zeta function. Here is a little more detail.
using Riemann’s analytic formula using a sum over the zeros of the zeta function. Here is a little more detail.
Firstly, if you can calculate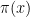 in polynomial time, then you can find a prime in polynomial time. Just start with the interval [x,2x] which is known to contain a prime, then do a binary search using the calculation of
in polynomial time, then you can find a prime in polynomial time. Just start with the interval [x,2x] which is known to contain a prime, then do a binary search using the calculation of  which requires
which requires 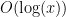 steps to pin down a prime.
steps to pin down a prime.
To calculate the formula is
the formula is
This needs to be calculated to sub-integer precision in polynomial time.
The first series has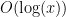 terms so we just need to calculate
terms so we just need to calculate 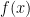 in polynomial time. This requires us to calculate each term of the main formula in polynomial time.
in polynomial time. This requires us to calculate each term of the main formula in polynomial time.
The logarithmic integral can be calculated using rapidly convergent series so there is no difficulty there. The last two terms are O(1) and easily found to sub-integer precision. This leaves just the sum over zeros to worry about.
We need to show that the sum can be calculated to sub-integer precision using only a polynomial number of terms, and that each zero can be found to sufficient precision in polynomial time.
This is where my knowledge falls short. I know that calculations of large numbers of zeros can be done in practice but it hard to get high precision. I also know that the sum is not absolutely convergent so it may require a trick to speed up the convergence rate. It may be necessary to assume RH to show that error terms vanish fast enough.
I know this is not the prettiest approach but I think it deserves to be investigated.
Comment by PhilG — August 12, 2009 @ 8:17 am |
Dear Phil, when you say “polynomial tine” do you mean in terms of x, or in terms of the number of digits of x?
Comment by Gil — August 12, 2009 @ 11:05 am |
I mnean polynomial in number of digits of x, i.e polynomial in log(x)
Comment by PhilG — August 12, 2009 @ 11:51 am |
Apropos this line of thought: the computational problem of finding small intervals on the famous line which contan a zero of the zeta function (i.e. demonstrating two values of opposite signs) where “small” is such that we expect say 1 zero in an interval of that length, is clearly of sufficient independent interest.
Unfortunately beside remembering the vast work by Odlyzko and others on actually finding zeros, I do not remember what is knowm regarding the complexity of the problem. Certainly if there is a polynimial algorithm in log x (even heuristically) this sounds very remarkable.
Comment by Gil Kalai — August 12, 2009 @ 12:24 pm |
Odlyzko has found nth zeros for n as high as and has calculated the first 100 zeros to over 1000 decimal places. This suggests that calculating a given zero to sufficient accuracy is possible in log(x) time. Sufficient accuracy just means to O(log(x)) decimal places. I think we’d have to consult a specialist like Odlyzko himself to know if there is any barrier when calculating a high n zero to high accuracy. I have not looked at the methods, just the results.
and has calculated the first 100 zeros to over 1000 decimal places. This suggests that calculating a given zero to sufficient accuracy is possible in log(x) time. Sufficient accuracy just means to O(log(x)) decimal places. I think we’d have to consult a specialist like Odlyzko himself to know if there is any barrier when calculating a high n zero to high accuracy. I have not looked at the methods, just the results.
I think the bottle neck is more likely to be the slow convergence of the series itself because it is not absolutely convergent. For a series of regular terms that is not absolutely convergent you can accelerate convergence by smoothing and extrapolating the partial sums, but the zeros of zeta are not very regular so that is not going to work well.
Even so, it looks like there is a faint hope that you might be able to find a prime in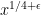 time if the speed of convergence is O(1/n) and is provable, and assuming RH of course.
time if the speed of convergence is O(1/n) and is provable, and assuming RH of course.
I’ve only looked at this in a cursory way because I am packing for summer hols, so I could have missed some other snag.
Comment by PhilG — August 12, 2009 @ 1:34 pm |
Here is what might happen.
Assuming that the values of the zeros can be calculated with enough accuracy sufficiently fast we just have to worry about how fast the sum over zeros converges. Since their distribution is uneven there is probably not much we can do to accelerate the convergence. Convergence is not absolute so typically the error term after summing n terms might be for some
for some 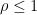 I’ll assume that
I’ll assume that  . Assuming RH the total of the sum is
. Assuming RH the total of the sum is 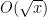 so the error term after n terms would be
so the error term after n terms would be  so to get sub-integer acuracy we would need
so to get sub-integer acuracy we would need 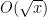 terms which is not fantastic.
terms which is not fantastic.
But suppose we just calculate the sum for the first terms. That would give an error term on
terms. That would give an error term on  which is
which is 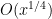 . We could use that to find a gap of size about
. We could use that to find a gap of size about 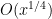 which must contain a prime. Then the job could be completed by testing each number in the interval using the primality test. This would give an algorithm for finding a prime at about
which must contain a prime. Then the job could be completed by testing each number in the interval using the primality test. This would give an algorithm for finding a prime at about 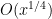 , Of course this is no good to us unless all the assumptions can be proven which might be a big ask.
, Of course this is no good to us unless all the assumptions can be proven which might be a big ask.
Comment by PhilG — August 12, 2009 @ 11:49 am |
Looking back at Emmanuel’s thread in comment 28, I see that I should have given you credit for having proposed the idea of computing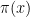 using zeros of
using zeros of 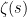 in what I wrote above in comment 35 (I somehow overlooked your comment). In fact, your comment was more pertinent to what I wrote than Emmanuel’s.
in what I wrote above in comment 35 (I somehow overlooked your comment). In fact, your comment was more pertinent to what I wrote than Emmanuel’s.
Anyways, as to your most recent comment, I seriously doubt that you will get an error as sharp as for
for  by computing zeros, especially if you only use the first
by computing zeros, especially if you only use the first  terms. The reason I say this is that in the usual explicit formula for
terms. The reason I say this is that in the usual explicit formula for 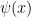 , if you truncate the sum up to height
, if you truncate the sum up to height  you get an error something like
you get an error something like  (times a log or two) in the formula for
(times a log or two) in the formula for  . And this error estimate has been known for ages, and not been improved upon; in fact, it is probably unimprovable.
. And this error estimate has been known for ages, and not been improved upon; in fact, it is probably unimprovable.
Now, if you truncate at height you should get an error of something like
you should get an error of something like  — much worse than
— much worse than  — which only allows you to locate primes in intervals of width
— which only allows you to locate primes in intervals of width  or so. The actual formula for the error in the explicit formula is something like
or so. The actual formula for the error in the explicit formula is something like  for
for 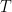 not too big (there is another term in the error estimate, which I can’t recall just now, but can be looked up on the internet). A good resource to consult is Harold Davenport’s “Multiplicative Number Theory”.
not too big (there is another term in the error estimate, which I can’t recall just now, but can be looked up on the internet). A good resource to consult is Harold Davenport’s “Multiplicative Number Theory”.
I realize you are using a different formula than the usual explicit formula for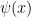 , but both formulas should give you the same information about
, but both formulas should give you the same information about 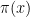 if you use the same set of zeros.
if you use the same set of zeros.
While I seriously doubt you will surpass the barrier, there is a very good chance to prove that you can locate primes of size
barrier, there is a very good chance to prove that you can locate primes of size  using
using 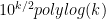 bit operations unconditionally.
bit operations unconditionally.
Comment by Ernie Croot — August 12, 2009 @ 1:31 pm |
Ernie, Sorry I had missed your comment 35 and I repeated stuff similar to what you already stated. I just got my formula for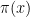 from wikipedia.
from wikipedia.
The reason I think that truncating after terms gives error terms of size
terms gives error terms of size  is that the size of the terms start at
is that the size of the terms start at  . This just comes from the fact that the real part of the zeros is 1/2 assuming RH. perhaps it works differently when looking at the formula for
. This just comes from the fact that the real part of the zeros is 1/2 assuming RH. perhaps it works differently when looking at the formula for 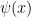
I am also assuming that the size of the terms goes down like 1/n and not slower. This is just a guess because I dont know enough about the shape of Li(x) for complex x, so that could be where my argument falls down.
Comment by PhilG — August 12, 2009 @ 2:04 pm |
Indeed, I wasn’t really thinking about such ideas when posting my comment #28.
In terms of the explicit formula, one may recall that by smoothing (i.e., summing primes with smoother weights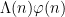 for suitable weight functions
for suitable weight functions  ), it can be made absolutely convergent easily without losing its prime-detection capability. I’m not sure if Davenport states such a general version in his book, but it’s been used extensively for various purposes, and one can see some versions e.g. in Th. 5.11 and 5.12 in my book with Iwaniec.
), it can be made absolutely convergent easily without losing its prime-detection capability. I’m not sure if Davenport states such a general version in his book, but it’s been used extensively for various purposes, and one can see some versions e.g. in Th. 5.11 and 5.12 in my book with Iwaniec.
As noted by Ernie in Comment #35, this doesn’t need RH. Actually for the original idea in #28, one might try to start by looking at a model case where RH is violated in a special way, say if there were just two non-critical zeros with real part 3/4. This would create a very dominant secondary term in the explicit formula that may be easy to analyze to see what may happen.
Comment by Emmanuel Kowalski — August 12, 2009 @ 2:47 pm |
If you are thinking about algorithmically computing the zeroes then you might be able to assume RH, since you will be checking it anyway as you go along. In other words, if the zeroes above height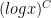 don’t contribute much to the explicit formula for counting primes in intervals around
don’t contribute much to the explicit formula for counting primes in intervals around  then you can have an unconditional algorithm which verifies the RH to the extent that it uses it.
then you can have an unconditional algorithm which verifies the RH to the extent that it uses it.
Comment by Lior — August 12, 2009 @ 6:15 pm |
I don’t think you will get the cancellation you hope for. You may get it for some specific values of that you can’t determine computationally, but that is not of much use as far as locating primes.
that you can’t determine computationally, but that is not of much use as far as locating primes.
Let me also point out that there may be a way to do something similar to all this (binary search using analytic formulas) without having to go through the messiness of working with the zeta function.
A prototype of what I mean here is the following observation (which won’t actually work as far as locating primes, but it suggests what is possible): using FFT’s I want to try to compute the sum of the divisor function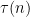 over all
over all  to an error of
to an error of  using something like
using something like  bit operations.
bit operations. bit operations). But now we can also do it computationally by fixing a modulus
bit operations). But now we can also do it computationally by fixing a modulus  , and then considering the exponential sum
, and then considering the exponential sum  , and then computing it at
, and then computing it at 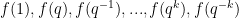 , where
, where  , and
, and  , say. Using FFT’s we can do this computation using something like
, say. Using FFT’s we can do this computation using something like 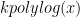 bit operations. Now once we have done this, using the usual Fourier methods applied to
bit operations. Now once we have done this, using the usual Fourier methods applied to  plus some extra terms that we don’t care about. Let
plus some extra terms that we don’t care about. Let 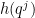 be the usual Fourier transform of the interval
be the usual Fourier transform of the interval 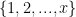 (perhaps we need to apply the usual smoothing to get the Fourier transform to have the usual strong decay properties) at the place
(perhaps we need to apply the usual smoothing to get the Fourier transform to have the usual strong decay properties) at the place  , and then sum up
, and then sum up  over, say,
over, say,  . All this can be done using
. All this can be done using 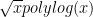 operations.
operations.
Now, of course, we know how to do this easily by using the “hyperbola method”, and we get a nice formula for this sum (so you really only need
Ok, so with FFT's we can quickly compute a divisor sum to high precision… big deal. But the same method should apply to loads of other arithmetical functions, some of which may allow us to locate primes directly, while others may imply a weak form of RH — low lying zeros must be near the half-line.
Comment by Ernie Croot — August 12, 2009 @ 3:21 pm |
I have been thinking about whether the Gil-Toa razor (post 40) rules out this method. I dont think it does because we start from a larger interval [x,2x] and use a binary search to narrow down a smaller interval that must contain a prime.
Suppose for example that we could calculate in
in 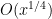 time with an
time with an 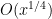 error term. Then we perform the binary search starting at [x,2x] which we know must contain
error term. Then we perform the binary search starting at [x,2x] which we know must contain  primes. At each step divide the interval in two and take the one with the largest number of primes according to our approxiamte formula for
primes. At each step divide the interval in two and take the one with the largest number of primes according to our approxiamte formula for  . Stop just before the number of primes given by the formula is twice the error term and we can be sure to have a prime in that interval.
. Stop just before the number of primes given by the formula is twice the error term and we can be sure to have a prime in that interval.
You might worry that we could hit a sparse region where the interval is actually bigger than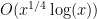 in size but because we always pick the half with the largest estimated number of primes and we know we started with
in size but because we always pick the half with the largest estimated number of primes and we know we started with  then this can’t happen.
then this can’t happen.
That just leaves the question of whether the calculation based on the zeros of the zeta function can give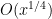 accuracy in
accuracy in 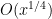 time. I will be out of touch for the next week but don’t let that stop anyone else checking the calculation.
time. I will be out of touch for the next week but don’t let that stop anyone else checking the calculation.
Comment by PhilG — August 12, 2009 @ 9:08 pm |
This is a response to Gil’s comment 36. I think your argument completely kills the suggestion I had. Let me say why (though I am not adding anything substantial to what you have already said).
Pick an integer . Our aim was to find a prime in the interval
. Our aim was to find a prime in the interval ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) , say, by choosing some
, say, by choosing some 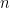 , quite a lot bigger than
, quite a lot bigger than  but not enormous (I was considering
but not enormous (I was considering 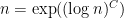 ), and then factorizing all the numbers between
), and then factorizing all the numbers between 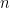 and
and  (where the second
(where the second 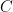 is not necessarily equal to the first, though one could just take the max of the two).
is not necessarily equal to the first, though one could just take the max of the two).
To see why a proof along these lines probably can’t work, let be any integer that’s substantially larger than
be any integer that’s substantially larger than  . For any
. For any  between
between  and
and  the number of multiples of
the number of multiples of  between
between  and
and  is roughly
is roughly  . To put that another way, the probability that a random integer between
. To put that another way, the probability that a random integer between  and
and  is a multiple of
is a multiple of  is roughly
is roughly 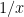 (and certainly at most
(and certainly at most  — that’s all we need for what I am about to say to work completely precisely). Therefore, if you choose a random integer between
— that’s all we need for what I am about to say to work completely precisely). Therefore, if you choose a random integer between  and
and  then its expected number of factors in the interval
then its expected number of factors in the interval ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) is about
is about  . Therefore, by linearity of expectation, if you choose a random subinterval
. Therefore, by linearity of expectation, if you choose a random subinterval ![[r,r+s]](https://s0.wp.com/latex.php?latex=%5Br%2Cr%2Bs%5D&bg=ffffff&fg=000000&s=0&c=20201002) of
of ![[m,2m]](https://s0.wp.com/latex.php?latex=%5Bm%2C2m%5D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where  is much less than
is much less than  , then the expected number of numbers between
, then the expected number of numbers between  and
and  that are factors of some number in the interval
that are factors of some number in the interval ![[r,r+s]](https://s0.wp.com/latex.php?latex=%5Br%2Cr%2Bs%5D&bg=ffffff&fg=000000&s=0&c=20201002) is at most about
is at most about  . If
. If  is substantially smaller than
is substantially smaller than  , then this is a tiny fraction of all the numbers between
, then this is a tiny fraction of all the numbers between ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
It follows that we can remove a tiny subset of![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) and end up with a set
and end up with a set ![A\subset[u,2u]](https://s0.wp.com/latex.php?latex=A%5Csubset%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that no number in the (generic) interval
such that no number in the (generic) interval ![[r,r+s]](https://s0.wp.com/latex.php?latex=%5Br%2Cr%2Bs%5D&bg=ffffff&fg=000000&s=0&c=20201002) is a multiple of any number in
is a multiple of any number in  . Therefore, any proof that there exists a number in
. Therefore, any proof that there exists a number in ![[r,r+s]](https://s0.wp.com/latex.php?latex=%5Br%2Cr%2Bs%5D&bg=ffffff&fg=000000&s=0&c=20201002) that has a factor in
that has a factor in ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) has to be a proof that uses in a very strong way the fact that we are dealing with every number in the interval
has to be a proof that uses in a very strong way the fact that we are dealing with every number in the interval ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Even removing a tiny subset of this interval can result in the conclusion being false.
. Even removing a tiny subset of this interval can result in the conclusion being false.
The reason I say that this kills my approach is twofold. First, I see no way of distinguishing between![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) and almost all of
and almost all of ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) , though actually I still wonder whether the very nice structure of the set of logarithms of numbers in this interval could give rise to something (though one has to be careful, since we all know that consipiracies can occur at very large integers such as
, though actually I still wonder whether the very nice structure of the set of logarithms of numbers in this interval could give rise to something (though one has to be careful, since we all know that consipiracies can occur at very large integers such as 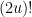 ). But then passing to the primes in
). But then passing to the primes in ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) seems completely hopeless, since my super-optimistic conjecture (comment 8) is utterly utterly false.
seems completely hopeless, since my super-optimistic conjecture (comment 8) is utterly utterly false.
Comment by gowers — August 12, 2009 @ 1:25 pm |
Annoying observation: WordPress doesn’t like latex n enclosed in dollars. It has to be latex {}n or latex \null n if you want it to parse. Oddly, other letters seem to be OK.
Comment by gowers — August 12, 2009 @ 1:32 pm |
According to the Terry Tao WordPress LaTeX bug collection thread this applies to 0 and some other single characters.
Comment by Jason Dyer — August 12, 2009 @ 1:55 pm |
I’ve been looking at the objections raised by Gil in #36 (and a very closely related objection of Troy in the #9 thread) and I think this argument is actually quite a general-purpose “razor” that eliminates quite a few proposed strategies. This is a bit discouraging, but it should help us in the long run by focusing attention on the remaining strategies that do have a chance of success.
To recap, the “generic prime razor” works like this: suppose one is trying to find primes in some explicit set (such as an interval [n,n+a]), or at least integers in that interval with a large prime factor. Suppose one imagines that all the primes associated to this interval are somehow “deleted”, rendering the task impossible. Can the proposed argument distinguish between the original set of primes, and the new set of “generic” primes in which all relevant primes are deleted? If not, then the argument cannot succeed.
For instance, suppose one wants to find a k-digit prime in at most steps (breaking the square root barrier). One can then build an explicit set of size
steps (breaking the square root barrier). One can then build an explicit set of size  consisting of numbers of poly(k) digits in size, and try to show that one of them is divisible by a prime of k digits or greater. But the number of primes that can do this (the “relevant” primes) is basically
consisting of numbers of poly(k) digits in size, and try to show that one of them is divisible by a prime of k digits or greater. But the number of primes that can do this (the “relevant” primes) is basically 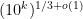 , whereas the total number of primes of k digits is
, whereas the total number of primes of k digits is  . Currently, we don’t seem to have any tools that can detect the removal of less than a square root number of primes, so this strategy seems to run into a serious obstruction.
. Currently, we don’t seem to have any tools that can detect the removal of less than a square root number of primes, so this strategy seems to run into a serious obstruction.
I thought at one point that this razor would cut away at Tim’s “adjustment” strategy (#13, #16, #21), but one could imagine that a sufficiently smart adjustment algorithm would be capable of “zeroing in” on the sparse set of relevant primes inside the set of all primes. It would have to be quite “smart”, though.
The razor may also impact the Riemann zeta strategy (#28, #35, #37): removing fewer than a square root number of primes does not seem to be easily detectable in the explicit formula relating primes with zeroes, though perhaps with a sufficiently “adaptive” strategy to zero in on the most promising area of primes, there may be a way to dodge the razor.
Ernie’s strategy in #10 using signed random sums seems to be totally immune to the razor, since it is not looking for large prime factors directly, but instead assuming that all numbers in the interval are smooth and obtaining a contradiction. Deleting the non-existent large relevant primes would thus not impact the strategy at all. So perhaps we should look at this strategy more.
The LLL strategy in #29 to construct nearby square-free numbers dodges the razor in an interesting way. If one wanted to find square-free numbers in a fixed short interval, then the razor could delete all the large prime factors of integers in this interval without anyone noticing, and basically one is forced to use small primes only to generate the square-free numbers. But the LLL strategy produces numbers that are close to each other, but not in any fixed short interval, so potentially all primes are in play.
Comment by Terence Tao — August 12, 2009 @ 4:44 pm |
I have a dynamical systems approach to the problem of, given a large number u and a larger number n (think of n as being a small power of u, say or
or  ), to find an integer near n that has a factor near u. There is a slight chance (assuming some equidistribution results on primes) that one may get a prime factor near u by this method, but I don’t understand the method well enough yet.
), to find an integer near n that has a factor near u. There is a slight chance (assuming some equidistribution results on primes) that one may get a prime factor near u by this method, but I don’t understand the method well enough yet.
Basically, the idea is to write n in base u. For instance, if , then we have
, then we have
for some a=O(1) and b, c in [0,u-1]. Note that this already shows that a number in [n-O(u),n] has the factor u, namely n-c. This is the trivial bound; I want to narrow the interval near n that one needs to search for to find a factor near u.
The idea is to decrement u to u-1 and see what happens to the digits a,b,c of n. Typically, what would happen is that a is unchanged, b goes to b+2a, and c goes to c+b+a. But sometimes there is wraparound, and so one has to perform a “carry” operation, subtracting u-1 from (say) c and adding 1 to b. But the point is that it is a fairly simple dynamical systems operation with a “nilpotent” flavour.
Now iterate this operation up to u/2 times, and see what happens to the final digit c. The hope is that one can use dynamical systems methods to show that c must equidistribute, and in particular must attain the size o(u) after fewer than u/2 steps. If so, we have shown that the interval [n-o(u),n] has an integer with a factor in [u/2,u], thus beating the trivial bound.
There are some results on equidistribution of nilpotent type sequences when specialised to the primes (e.g. Ben and I have a paper on this topic), but the bounds are quite weak (they get a bit better with GRH, though). So if we can achieve equidistribution on the integers there is some chance to extend it to the primes also.
Comment by Terence Tao — August 12, 2009 @ 6:00 pm |
It occurs to me that we don’t have to necessarily blindly decrement u here, but can be smarter and jump ahead to a favourable choice of u. For instance, suppose that we could show that equidistribution of c improves when b/u behaves in a “Diophantine” manner. One could then restrict attention to a region of u’s where b/u look Diophantine, and then search around there. The point is that we don’t really need equidistribution, we just need some sort of algorithm that allows us to move c closer to zero.
Comment by Terence Tao — August 12, 2009 @ 6:04 pm |
If you have the consequences of this theorem not being true then you have all constructable numbers are are surrounded by k^100 numbers which are not prime and themselves are not prime. Now if the abc conjecture holds the a smooth number can be found and added to the k^100 numbers
and if the smooth number was much smaller than k^100 the result would be that slightly less than 50% of the k^100 numbers would be rough. In fact more than that you would get pairs of numbers one of which would be rough. Perhaps this would be of use in the main problem or some of the weaker ones.
Comment by Kristal Cantwell — August 12, 2009 @ 6:38 pm |
Let me make a somewhat obtuse comment, which nonetheless might lead to an algorithm to find primes of size in time
in time  : one reason that we can’t analytically prove that intervals
: one reason that we can’t analytically prove that intervals ![[x, x + \sqrt{x}]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x+%2B+%5Csqrt%7Bx%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) contain primes is that even assuming RH the error term in the explicit formula for
contain primes is that even assuming RH the error term in the explicit formula for  is size
is size 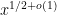 (
( or so). And we have a similar phenomena for all sorts of arithmetic problems. For example, working in finite fields and using Gauss sums — which have “square root cancellation” (much like
or so). And we have a similar phenomena for all sorts of arithmetic problems. For example, working in finite fields and using Gauss sums — which have “square root cancellation” (much like 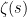 back in the complex numbers arena) — along with the usual Fourier methods, the best we can show is that the sum of
back in the complex numbers arena) — along with the usual Fourier methods, the best we can show is that the sum of  Legendre symbols over an interval, has size
Legendre symbols over an interval, has size 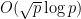 or so.
or so.
But now there is an extra set of tricks that we seem to have in finite fields . For example, using the Weil estimates for high genus curves, Burgess was able to show that intervals of width down to
. For example, using the Weil estimates for high genus curves, Burgess was able to show that intervals of width down to 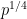 contain loads of quadratic residues and non-residues. As I recall (maybe what I am about to write is nonsense, but if so it has some truth) he used high moments of sums of Legendre symbols over intervals, expanded the power, swapped the order of multiple summations, and then has some sums like
contain loads of quadratic residues and non-residues. As I recall (maybe what I am about to write is nonsense, but if so it has some truth) he used high moments of sums of Legendre symbols over intervals, expanded the power, swapped the order of multiple summations, and then has some sums like 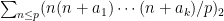 that he had to evaluate. This can be done by relating the sum to the curve
that he had to evaluate. This can be done by relating the sum to the curve  , which is where the Weil estimates came in.
, which is where the Weil estimates came in.
Now, the original problem of Gauss sums and FOurier methods I think can be rephrased as a question about the finite field zeta function for the curve ; and similarly, Burgess’s method can be rephrased, I think, in terms of finite field zeta functions involving the curves
; and similarly, Burgess’s method can be rephrased, I think, in terms of finite field zeta functions involving the curves  .
.
What all this suggests is that there should be an analogue of Burgess’s idea back in the prime numbers realm of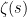 . Maybe by assuming the RH for certain L-functions associated to curves, one can somehow translate Burgess’s idea to the prime numbers, to show that intervals of width
. Maybe by assuming the RH for certain L-functions associated to curves, one can somehow translate Burgess’s idea to the prime numbers, to show that intervals of width  contain primes, leading to the
contain primes, leading to the  running time stated above.
running time stated above.
I am too busy right now to sort all this out myself (I have to referee some papers, write my grant proposal, and resume teaching next week). If what I say isn’t complete nonsense, then I hope someone will investigate this.
Comment by Ernie Croot — August 13, 2009 @ 2:00 am |
Let me point out something else that is strange about Burgess’s method. I think it somehow gets around “Gil’s razor”, because if you change the values of Legendre symbols at, say,
at, say, 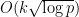 places, it has a negligible effect on the size of the corresponding Weil sums. Yet, Burgess just uses these upper bounds (and perhaps a trick or two I don’t recall just now) and gets equidistribution of Legendre symbols in intervals of width
places, it has a negligible effect on the size of the corresponding Weil sums. Yet, Burgess just uses these upper bounds (and perhaps a trick or two I don’t recall just now) and gets equidistribution of Legendre symbols in intervals of width 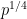 .
.
Also, one may try to be less ambitious about combining together the information for multiple zeta functions to pin down primes in short intervals, and instead just try to translate Burgess’s idea to the integers by using some strong form of the Hardy-Littlewood conjecture, where the error terms are of size . I think even showing that intervals as short as
. I think even showing that intervals as short as  always contain primes, conditional on this strong (but not too strong) H-L conjecture, would be interesting.
always contain primes, conditional on this strong (but not too strong) H-L conjecture, would be interesting.
Comment by Ernie Croot — August 13, 2009 @ 3:25 pm |
Let f(x,y,…,w) be an irreducible polynomial with integer coefficients. For concreteness, let it be a homogeneous irreducible polynomial f(x,y) with integer coefficients, say. If we choose x and y at random between 1 and N, then the probability that f(x,y) be prime is about the same as the probability that a random integer of size N be a prime (namely, 1/(log N)), up to a constant factor due to local reasons. (Actually, that factor can be 0 if f is chosen perversely, but never mind that.) However, if we choose an integer n uniformly and at random among the values taken by f(x,y) for 1<=x,y<=N integers, the probability that n be prime could be much higher than 1/(log N). For example, take f(x,y)=x^2+y^2;
half of all primes up to N are of the form x^2 + y^2, but only about
N/(log N)^(1/2) integers up to N are of the form x^2 + y^2, and thus an integer taken uniformly and at random among integers of the form x^2+y^2
has a probability of about 1/(log N)^{1/2} of being prime.
Questions:
(1) Is there any way to choose an integer uniformly and at random (or nearly uniformly and at random) among the integers<=N represented by a form f(x,y)?
(2) Say that we increase the degree of f (and the number of variables) in the hope of making the probability 1/(log N)^{1/2} higher. Of course, things become more computationally expensive in the process. How expensive do they become?
What can we hope to obtain out of this game? I suppose we can get "models" for the integers that contain higher and higher densities of primes, but where does that get us?
Comment by Harald Helfgott — August 13, 2009 @ 2:15 am |
There is a theorem of Erdos (with a long list of improvements) which states the following.
Let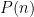 denote the largest prime factor of
denote the largest prime factor of  and
and  denote the number of primes less than
denote the number of primes less than  satisfying
satisfying  . We then have that
. We then have that  for some particular choices of
for some particular choices of 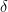 , where
, where 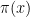 denotes the usual prime counting function.
denotes the usual prime counting function.
Friedlander has obtained this with , while Baker and Harmen have improved this to
, while Baker and Harmen have improved this to  (strictly speaking, they proved something slightly weaker, but in his mathscinet review Friedlander suggests that this probably follows from their methods). A particular application in the Baker and Harmen paper, which might be of interest here, is the existence of infinitely many primes
(strictly speaking, they proved something slightly weaker, but in his mathscinet review Friedlander suggests that this probably follows from their methods). A particular application in the Baker and Harmen paper, which might be of interest here, is the existence of infinitely many primes 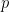 such that
such that 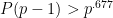 . These theorems seem very close to our project, however it isn’t clear to me how to use them directly. Let me admit now that I haven’t dug into these results past the mathscinet reviews.
. These theorems seem very close to our project, however it isn’t clear to me how to use them directly. Let me admit now that I haven’t dug into these results past the mathscinet reviews.
One attempt at making use of the Erdos-type result, would be to try to use it to more cleverly search an interval in which we know there is a prime of the given form. Since we know that there is a prime in![[x, x+x^{.53}]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2Bx%5E%7B.53%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) , the Erdos-type result is close to giving that there is a prime, p, in
, the Erdos-type result is close to giving that there is a prime, p, in ![[x, x+ cx^{.53}]](https://s0.wp.com/latex.php?latex=%5Bx%2C+x%2B+cx%5E%7B.53%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) such that
such that  . Let's assume that this is true, and that
. Let's assume that this is true, and that  . Moreover, let us assume that no power of
. Moreover, let us assume that no power of  divides
divides  . (I don't think this assumption will be a problem since we can iterate the following argument over all possible powers of
. (I don't think this assumption will be a problem since we can iterate the following argument over all possible powers of  .)
.)
On these assumptions we have that![P(p+1) \in [x^{.3}, (x+cx^{.53})^{.3} ] \subset [x^{.3}, x^{.3}+x^{.53\times .3} ]](https://s0.wp.com/latex.php?latex=P%28p%2B1%29+%5Cin+%5Bx%5E%7B.3%7D%2C+%28x%2Bcx%5E%7B.53%7D%29%5E%7B.3%7D+%5D+%5Csubset+%5Bx%5E%7B.3%7D%2C+x%5E%7B.3%7D%2Bx%5E%7B.53%5Ctimes+.3%7D+%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Thus we should be able to search this interval for primes in
. Thus we should be able to search this interval for primes in  steps. Every time we find a prime we check every integer of the form
steps. Every time we find a prime we check every integer of the form  for primality for each
for primality for each  such that
such that ![p\times n-1 \in [x, x+ cx^{.53}]](https://s0.wp.com/latex.php?latex=p%5Ctimes+n-1+%5Cin+%5Bx%2C+x%2B+cx%5E%7B.53%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) . This search space is largest when
. This search space is largest when  , in which case we need to search through the interval
, in which case we need to search through the interval ![[x^{.7}, x^{.7}+c x^{.23}]](https://s0.wp.com/latex.php?latex=%5Bx%5E%7B.7%7D%2C+x%5E%7B.7%7D%2Bc+x%5E%7B.23%7D%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Thus the total run time should be
. Thus the total run time should be 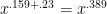 , which would bring us to around
, which would bring us to around  .
.
The Baker Harmen paper is: Baker, Harmen, Shifted primes without large prime factors, Acta Arith. 83 (1998), no. 4, 331–361.
Comment by Mark Lewko — August 13, 2009 @ 2:31 am |
I think one would need an extremely strict interpretation of the “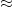 ” symbol in
” symbol in 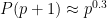 for this to work. Suppose for instance that one could only obtain
for this to work. Suppose for instance that one could only obtain  between
between  and
and  , then the size of the search space for
, then the size of the search space for  jumps up from
jumps up from  to
to 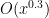 , which brings us back over the square root barrier.
, which brings us back over the square root barrier.
In fact, heuristically the proportion of numbers which contain a prime factor in a range [y,2y] should be about (by the prime number theorem), so getting a prime factor in a largish interval should only cuts down the size of the search space by a logarithm or so. (Getting a prime factor in a short interval would be much more restrictive, but perhaps beyond the Baker-Harmen technology.)
(by the prime number theorem), so getting a prime factor in a largish interval should only cuts down the size of the search space by a logarithm or so. (Getting a prime factor in a short interval would be much more restrictive, but perhaps beyond the Baker-Harmen technology.)
Comment by Terence Tao — August 13, 2009 @ 4:16 pm |
One problem which can be identified from the above discussion and certainly arose in other contexts is:
What is special about the sequence (or the set) S described by log p_k k=1,2,…
Perhaps the first place that this question naturally comes to mind is that after looking at elementary proofs of the prime number theorem which use rather general properties of this sequence one ask oneself : what can imply the conjectural better properties say of mebius functions? So the first question would be
How can you distinguish between S and a dense random subset of S?
(All the nice properties of zeta functions seem to vanish for random subsets of primes}
We also want to distinguish between S and subsets of S where we delete all primes involved in a small interval.
One idea we can play with (and probably people did played with but I dont know about it)is to look at sets S’ which mimmick the wonderful periodic property of all sums in S. (We can forget about the logs and ask it in terms of products.)
Suppose you have a set of real numbers T so that the products of distinct elements from T ordered in a sequence a_i satisfies, say, a_{i+1}-a_i is between 0.9 to 1.1 for every i. (Or some stronger proerty. We can formulate it for log T if we prefer.) Does this already gives us nice conjectural properties of primes? (RH, Cramer’s model,etc)
Comment by Gil Kalai — August 13, 2009 @ 7:53 am |
It occur to me that I do not know (and this may represent a big gap in my education) if there is any sequence of real numbers so that the distinct products satisfies the above condition which is not “essentially” the sequence of primes. Hmmm,
primes which are 1(mod 3) also gives an example; i’ll better ask around.update (8/14): actually I am not aware of any example of Beurling primes (see Terry’s comment below), where the associated Beurling integers satisfy the above condition: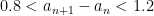 , where the Beurling primes are not ashkara (=precisely) the primes.
, where the Beurling primes are not ashkara (=precisely) the primes.
Comment by Gil — August 13, 2009 @ 9:36 am |
It sounds like you want the theory of the Beurling primes – sets of positive reals whose products are distributed like the integers. Unfortunately, there are examples of such sets which have reasonably good distribution properties (e.g. number of “Beurling integers” less than x is x + O(x^{0.99}) but fail to obey RH or even any nontrivial improvement to the classical prime number theorem (which Beurling proved to be true for all Beurling primes). There is a fair amount of literature on this; a Google search turned up for instance this recent paper of Hilberdink.
It may well be that if one insists (as you do) that the error term is O(1) then one is forced to be so close to the actual primes that one should presumably have all the good properties that the actual primes have, but I don’t know of any literature in this direction.
Comment by Terence Tao — August 13, 2009 @ 4:08 pm |
Thanks! I suppose we can ask our pronlem abstractly for Beurling primes where we have cost 1 for finding the nth “integer”, testing “primality” and (perhaps) “factoring”.
I remembered vagely a proof by Renyi to PNT which used very little about primes and it may be related to Beurling result. I also remember vaguely that even if you take every prime with probability 1/2, conjectures for primes beyond the PNT fails.
My question was in trying to suggest how to save additive NT methods against the razor.
The “Liphshitz” or “no large gaps” condition looks very strong. Even if you delete m primes you create by the Chinese remainder theorem a gap of length m near their product. But our razor which was based on deleting all large primes involved in an interval of length k^3 (say) of k-digits integers amounts to creating unusually large gaps. So there is a (small) hope that some additive number theory methods (or other methods) can exploit somehow a “no gaps” condition or a “no unusually large gaps” condition.
Comment by Gil Kalai — August 13, 2009 @ 9:44 pm |
Continuing the line of thought from Gil’s comment 36 and Terry’s comments 40 and 41, I find the following analogy helpful, when it comes to the simpler problem of trying to prove that in the interval![[n,n+(\log n)^C]](https://s0.wp.com/latex.php?latex=%5Bn%2Cn%2B%28%5Clog+n%29%5EC%5D&bg=ffffff&fg=000000&s=0&c=20201002) there must be an integer with a factor (not necessarily prime) in the interval
there must be an integer with a factor (not necessarily prime) in the interval ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) , where
, where  is substantially smaller than
is substantially smaller than  but not too too small.
but not too too small.
What Gil’s argument shows is that we cannot afford to throw away even a tiny part of the set![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) (at least in the worst case). However, as I vaguely remarked, and as Terry much more precisely pointed out, that doesn’t rule out a “smart” approach. What I want to mention here is a similar situation in which a “smart” approach exists.
(at least in the worst case). However, as I vaguely remarked, and as Terry much more precisely pointed out, that doesn’t rule out a “smart” approach. What I want to mention here is a similar situation in which a “smart” approach exists.
Consider the problem of trying to approximate an arbitrary real number in the interval
in the interval ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=000000&s=0&c=20201002) by an integer combination of
by an integer combination of  and
and  . We would like to get to within
. We would like to get to within  of
of  using a combination
using a combination  , with
, with  and
and 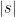 both at most
both at most  . General theory of continued fractions tells us that we can get to within
. General theory of continued fractions tells us that we can get to within  , which is roughly telling us that the numbers
, which is roughly telling us that the numbers 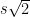 are so well-separated mod 1 that the trivial pigeonhole bound is actually best possible to within a constant.
are so well-separated mod 1 that the trivial pigeonhole bound is actually best possible to within a constant.
But we could run Gil’s argument here and say that in an interval of length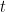 the expected number of points of the form
the expected number of points of the form  is about
is about  . So in general we could remove a tiny number of integer pairs
. So in general we could remove a tiny number of integer pairs  and then it would be impossible to approximate
and then it would be impossible to approximate  . In other words, we have a strong approximate linear independence, so, unsurprisingly, we have a more or less unique way of approximating anything. It still seems reasonable to hope that something like that could happen for the problem of approximating
. In other words, we have a strong approximate linear independence, so, unsurprisingly, we have a more or less unique way of approximating anything. It still seems reasonable to hope that something like that could happen for the problem of approximating 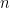 .
.
This ties in with Terry’s dynamical approach, since the above example corresponds to the dynamical system where you rotate the circle by .
.
There’s one problem I don’t yet see how to get round, which is that if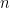 is much bigger than
is much bigger than  then we don’t get a good distribution:
then we don’t get a good distribution: 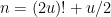 is a trivial example. But how does one properly use the fact that
is a trivial example. But how does one properly use the fact that 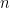 is smaller than that?
is smaller than that?
Got to dash now.
Comment by gowers — August 13, 2009 @ 9:13 am |
If one uses the “base u” approach then the fact that n is small is reflected in the fact that there are only a few digits in the base u expansion of n, which keeps the relevant dynamical system approximately “polynomial” of low degree. If n is less than u^2, then one has a linear dynamical system not too dissimilar from the rotation by example. What this system tells us is that if
example. What this system tells us is that if  , then there is an integer within
, then there is an integer within 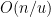 of n which has a factor near u, but this is trivial since having a factor near u is the same as having a factor near n/u.
of n which has a factor near u, but this is trivial since having a factor near u is the same as having a factor near n/u.
Comment by Terence Tao — August 13, 2009 @ 4:41 pm |
Continuing the continued-fraction analogy, but also very much bearing in mind Terry’s dynamical-systems idea (comment 41), here is a heuristic argument that might lead one to expect at least some fairly non-trivial bound for the problem of approximating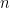 by a multiple of something in
by a multiple of something in ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Let’s do roughly what Terry suggested, but instead of writing
. Let’s do roughly what Terry suggested, but instead of writing 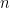 in base
in base  , we’ll simply write it modulo
, we’ll simply write it modulo  . That gives us the trivial bound that we can approximate
. That gives us the trivial bound that we can approximate 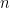 to within
to within  . We now consider the behaviour of the sequence
. We now consider the behaviour of the sequence  . When will
. When will  be small? When
be small? When  is surprisingly close to an integer. I’m already in trouble here, as I don’t see any reason against some conspiracy that would cause
is surprisingly close to an integer. I’m already in trouble here, as I don’t see any reason against some conspiracy that would cause  never to be close to an integer. Indeed, the thought that I started this comment with, that the sequence might have some structure that would cause it to be close to an integer on a subset that had a nice property, so that one could iterate (rather like what happens when one tries to approximate a real number by a rational) is not obviously correct. (That doesn’t have any bearing on whether Terry’s is correct — his
never to be close to an integer. Indeed, the thought that I started this comment with, that the sequence might have some structure that would cause it to be close to an integer on a subset that had a nice property, so that one could iterate (rather like what happens when one tries to approximate a real number by a rational) is not obviously correct. (That doesn’t have any bearing on whether Terry’s is correct — his  is much larger and his approach is somewhat different.)
is much larger and his approach is somewhat different.)
Here’s a possible way of killing off completely what I’m trying to do here. One could find a convex function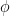 that was somehow “nice” in the way that
that was somehow “nice” in the way that  is nice, has a similar growth rate, but has the property that
is nice, has a similar growth rate, but has the property that 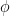 of the interval
of the interval ![[u,2u]](https://s0.wp.com/latex.php?latex=%5Bu%2C2u%5D&bg=ffffff&fg=000000&s=0&c=20201002) of integers leaves gaps even when you take a k-fold sumset for some quite large k. I don’t think I have had any thoughts that would distinguish between
of integers leaves gaps even when you take a k-fold sumset for some quite large k. I don’t think I have had any thoughts that would distinguish between  and
and 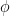 .
.
Comment by gowers — August 13, 2009 @ 11:49 am |
Just happen to visit this polymath project. Don’t know if the following is of any help or relevance.
It seems that I may have worked on what Gower’s comment 48 in “Finding Almost Squares III” that [n – o(u), n] contains an integer divisible by some integer in [u, 2u] using his idea n mod u, n mod u+1, n mod u+2, … If interested, you may check the arXiv.
Also regarding the problem of finding an integer in [n, n + (log n)^C] containing a factor in [u, 2u], you may check “Finding Almost Squares IV” at Archiv der Mathematik, 92 (2009), 303-313. Probably it is not of much help as it is just an almost all result and no algorithm is given to find such an n.
Comment by Tsz Ho Chan — August 13, 2009 @ 4:20 pm |
It seems that the most relevant paper in this series for us is the first paper,
http://www.ams.org/mathscinet-getitem?mr=2218342
though my university does not have a subscription to this year of the journal.
The reviewer does however notes an elementary way to attain the square root bound here, or more precisely to show that given any u (not necessarily integer), there is an integer in![[u^2 - O(\sqrt{u}), u^2 + O(\sqrt{u})]](https://s0.wp.com/latex.php?latex=%5Bu%5E2+-+O%28%5Csqrt%7Bu%7D%29%2C+u%5E2+%2B+O%28%5Csqrt%7Bu%7D%29%5D&bg=ffffff&fg=000000&s=0&c=20201002) with a factor in
with a factor in ![[u-O(\sqrt{u}), u+O(\sqrt{u})]](https://s0.wp.com/latex.php?latex=%5Bu-O%28%5Csqrt%7Bu%7D%29%2C+u%2BO%28%5Csqrt%7Bu%7D%29%5D&bg=ffffff&fg=000000&s=0&c=20201002) . Indeed, one lets
. Indeed, one lets  be the first integer larger than u, thus
be the first integer larger than u, thus  ; then one lets
; then one lets 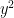 be the closest square number to
be the closest square number to  , thus
, thus 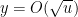 and
and 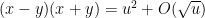 , as claimed. (Note that this improves upon the Gauss circle problem type argument I had in #7, where I needed an interval of size
, as claimed. (Note that this improves upon the Gauss circle problem type argument I had in #7, where I needed an interval of size  or so.)
or so.)
If one could somehow adapt this argument to primes instead of integers, we could attain the square root barrier without using RH.
In the above paper, apparently the square root barrier is broken assuming some strong exponential sum bound relating to the equidistribution of modulo 1 (this seems reminiscent of the dynamical systems approach).
modulo 1 (this seems reminiscent of the dynamical systems approach).
Comment by Terence Tao — August 13, 2009 @ 4:37 pm |
Just a little comment regarding the factoring oracle/additive combinatorics approach. What we did was to look at an interval of length k^5 of k digits numbers; and to conjecture that some number in the interval has a large prime factor. (Where “large” can be a number with at least m digits for m= k/log k or even just m=k^{1/3} numbers.)
A weaker conjecture that will be as fine for us is this: if we start with an interval of length k^5 and consider the set S of all m-digit or more factors (not necessarily primes) of all the numbers in the intervals; then there will be an m-digit prime factor for a number in S+S.
In other words, we can allow several interations of the operations: “taking sums” and “taking factors”.
The razor is as bad to this idea as it was for the original one. But if we can somehow find a way around the razor, this extension can be helpful because the sum/product theorems suggest that you can do more if you allow more than one arithmetic operation.
Comment by Gil — August 14, 2009 @ 6:14 am |
[…] finding primes, research — Terence Tao @ 5:10 pm Tags: polymath4 This is a continuation of Research Thread II of the “Finding primes” polymath project, which is now full. It seems that we are […]
Pingback by (Research Thread III) Determinstic way to find primes « The polymath blog — August 13, 2009 @ 5:10 pm |
As this thread is now quite full, I am opening a new research thread for this project at
Comment by Terence Tao — August 13, 2009 @ 5:12 pm |
[…] https://polymathprojects.org/2009/08/09/research-thread-ii-deterministic-way-to-find-primes/ […]
Pingback by Polymath4 « Euclidean Ramsey Theory — August 13, 2009 @ 11:54 pm |
[…] meantime, Terence Tao started a polymath blog here, where he initiated four discussion threads (1, 2, 3 and 4) on deterministic ways to find primes (I’m not quite sure how that’s […]
Pingback by Polymath again « What Is Research? — October 27, 2009 @ 11:38 pm |
[…] Polymath4 is devoted to a question about derandomization: To find a deterministic polynomial time algorithm for finding a k-digit prime. So I (belatedly) devote this post to derandomization and, in particular, the following four problems. […]
Pingback by Four Derandomization Problems « Combinatorics and more — December 6, 2009 @ 9:30 am |
[…] skeptical and enthusiastic. (August 2009) polymath4 dedicated to finding primes deterministically was launched over the polymathblog. (Polymath4 was very active for several months. It led to some fruitful […]
Pingback by Mathematics, Science, and Blogs « Combinatorics and more — January 9, 2010 @ 11:06 pm |
one (dumb) approach to solving problem 1 and 2, assuming you can detect whether or not a number is prime fairly quickly, would be the following.
start off with a binary number c bits long, containing all 1’s. test for prime. change the lowest bit to 0. test for prime. change the second lowest bit to 0. test for prime. change the lowest bit back to 1, test for prime. continue changing 1 bit at a time and testing for prime. in the worst case, it will take 2^(c/2) changes to find a prime. for problem 1, this means that you can find a prime of size log_2(k) in k time. for problem 2, this means you can find the largest prime of size log_2(k) in k steps.
Comment by Phillip Brix — March 6, 2012 @ 6:51 pm |