It’s time for another rollover of the Polymath7 “Hot Spots” conjecture, as the previous research thread has again become full.
Activity has now focused on a numerical strategy to solve the hot spots conjecture for all acute angle triangles ABC. In broad terms, the strategy (also outlined in this document) is as follows. (I’ll focus here on the problem of estimating the eigenfunction; one also needs to simultaneously obtain control on the eigenvalue, but this seems to be to be a somewhat more tractable problem.)
- First, observe that as the conjecture is scale invariant, the only relevant parameters for the triangle ABC are the angles
, which of course lie between 0 and
and add up to
. We can also order
, giving a parameter space which is a triangle between the values
.
- The triangles that are too close to the degenerate isosceles triangle
or the equilateral triangle
need to be handled by analytic arguments. (Preliminary versions of these arguments can be found here and Section 6 of these notes respectively, but the constants need to be made explicit (and as strong as possible)).
- For the remaining parameter space, we will use a sufficiently fine discrete mesh of angles
; the optimal spacing of this mesh is yet to be determined.
- For each triplet of angles in this mesh, we partition the triangle ABC (possibly after rescaling it to a reference triangle
, such as the unit right-angled triangle) into smaller subtriangles, and approximate the second eigenfunction
(or the rescaled triangle
) by the eigenfunction
(or
) for a finite element restriction of the eigenvalue problem, in which the function is continuous and piecewise polynomial of low degree (probably linear or quadratic) in each subtriangle; see Section 2.2 of these notes. With respect to a suitable basis,
can be represented by a finite vector
.
- Using numerical linear algebra methods (such as Lanczos iteration) with interval arithmetic, obtain an approximation
to
, with rigorous bounds on the error between the two. This gives an approximation to
or
with rigorous error bounds (initially of L^2 type, but presumably upgradable).
- After (somehow) obtaining a rigorous error bound between
and
(or
and
), conclude that
stays far from its extremum when one is sufficiently far away from the vertices A,B,C of the triangle.
- Using
stability theory of eigenfunctions (see Section 5 of these notes), conclude that
stays far from its extremum even when
is not at a mesh point. Thus, the hot spots conjecture is not violated away from the vertices. (This argument should also handle the vertex that is neither the maximum nor minimum value for the eigenfunction, leaving only the neighbourhoods of the two extremising vertices to deal with.)
- Finally, use an analytic argument (perhaps based on these calculations) to show that the hot spots conjecture is also not violated near an extremising vertex.
This all looks like it should work in principle, but it is a substantial amount of effort; there is probably still some scope to try to simplify the scheme before we really push for implementing it.
It seems that one of the weaker links in the above process, at least at our current level of understanding, is Step 6. If we had L^2 bounds on the residual , then one could get H^2 (and thence L^infty) bounds on the error
, then one could get H^2 (and thence L^infty) bounds on the error  , but with piecewise polynomial approximations that are only continuous at the edges,
, but with piecewise polynomial approximations that are only continuous at the edges,  is going to have some singular components on the edges of the triangle and so L^2 bounds for the residual are not available.
is going to have some singular components on the edges of the triangle and so L^2 bounds for the residual are not available.
On the other hand, if we get really good bounds for Step 6, then maybe these bounds would also work for perturbations of the triangle and we could skip Step 7.
Comment by Terence Tao — September 10, 2012 @ 7:36 pm |
There are two pieces to Step 6.
part a. Denote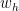 as the discrete approximant of
as the discrete approximant of 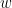 from the finite-dimensional subspace
from the finite-dimensional subspace  , where
, where 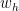 is computed by solving the discrete eigenvalue problem DVP2 exactly.
is computed by solving the discrete eigenvalue problem DVP2 exactly.
part b. Denote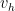 as the approximation of
as the approximation of 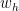 , computed using an iterative process for computing eigenfunctions of discrete systems.
, computed using an iterative process for computing eigenfunctions of discrete systems.
What we need is a rigorous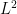 estimate on the residual
estimate on the residual  , since what we have in hand is
, since what we have in hand is 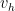 .
. , since
, since 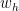 is approximating a
is approximating a 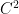 function, and can try to post some notes/references.
function, and can try to post some notes/references.
I think one can use inverse and duality estimates to compute the finite element residual
If we denote the quantity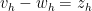 , then we want
, then we want 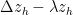 to be well-controlled. We only have in hand
to be well-controlled. We only have in hand  and
and 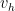 , so the error estimate we want will have to boot-strap from these.
, so the error estimate we want will have to boot-strap from these.
Apart from using interval arithmetic, I’m not sure how to proceed on this. Insight into part b. is key.
Comment by nilimanigam — September 12, 2012 @ 5:11 pm |
One possibility is to not work with residuals, but instead with the Rayleigh quotient of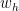 (which is finite, because it only requires square integrability of the first derivative of w_h, not square integrability of the second derivative). If this Rayleigh quotient is known to be close to the true second eigenvalue
(which is finite, because it only requires square integrability of the first derivative of w_h, not square integrability of the second derivative). If this Rayleigh quotient is known to be close to the true second eigenvalue 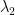 , then
, then 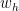 is necessarily close in H^1 norm to a true second eigenfunction. On the plus side, this lets us skip Steps 6 and 7 (since the Rayleigh quotient is quite stable wrt perturbation of the triangle) and would be relatively simple to implement.
is necessarily close in H^1 norm to a true second eigenfunction. On the plus side, this lets us skip Steps 6 and 7 (since the Rayleigh quotient is quite stable wrt perturbation of the triangle) and would be relatively simple to implement.
On the minus side, it only gives H^1 control on the true eigenfunction, which isn’t quite enough by itself to give L^infty control. But perhaps we can combine it with some elliptic regularity or something. For instance, in any disk in the triangle ABC, one can write the value of the eigenfunction at the centre of the the disk in terms of an integral on the disk involving a Bessel function. So if one has H^1 control on the eigenfunction in that disk, one gets pointwise control at the centre of the disk. If one is near an edge of the triangle, but not near a corner, one can do something similar after first applying a reflection. Things get worse near the corners, but we were planning to use a different argument for that case anyway (Step 8).
Another minus is that I suspect the dependence of the error on the mesh size is poor (something like the square root of the mesh size, perhaps). And it requires quite precise control on the second eigenvalue. But it may still be the lesser of two evils.
Comment by Terence Tao — September 14, 2012 @ 5:18 am |
Let’s see. For a symmetric positive-definite , the Lanzcos iteration for the smallest eigenvalue of
, the Lanzcos iteration for the smallest eigenvalue of 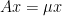 proceeds until a certain error criteria is met. This error criteria is based on the discrete Rayleigh quotient
proceeds until a certain error criteria is met. This error criteria is based on the discrete Rayleigh quotient  ($v$ is assumed to be normalized).
($v$ is assumed to be normalized).
In our setting, the quantity is the quantity
is the quantity 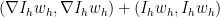 , where I am using the notation
, where I am using the notation 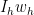 to be the element of
to be the element of 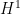 constructed by using the coefficients
constructed by using the coefficients 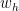 in some basis.
in some basis.
In other words, the algorithm already minimizes the discrete Rayleigh quotient. The nature of the matrix tells us that the true discrete eigenvalue converges to the true one (for the continuous one) quadratically in the mesh size. The asymptotic constant depends on the true eigenvalue and the spectral gap. Eigenvectors converge quadratically with tesselation size in the H1 norm, eigenvalues converge quartically.
tells us that the true discrete eigenvalue converges to the true one (for the continuous one) quadratically in the mesh size. The asymptotic constant depends on the true eigenvalue and the spectral gap. Eigenvectors converge quadratically with tesselation size in the H1 norm, eigenvalues converge quartically.
Backward error analysis tells us that the computed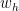 is close to the true
is close to the true 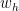 for a given matrix size. The asymptotic constant again depends on the spectral gap. http://web.eecs.utk.edu/~dongarra/etemplates/node151.html
for a given matrix size. The asymptotic constant again depends on the spectral gap. http://web.eecs.utk.edu/~dongarra/etemplates/node151.html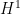 control, and I should attempt to explicitly string together the constants.
control, and I should attempt to explicitly string together the constants.
So I think we already have
I suspect you may be right: since the asymptotic constants above for any FIXED triangle PQR depend on the spectral gap, and since this spectral gap varies as we change the angles of PQR, we may have poor control in terms of the angle parameters. But staring at the spectral gap plot

I am optimistic that away from the equilateral triangle one could actually make the dependence of asymptotic constants precise.
What’s harder to get a hand on is the residual of the computed (ie, not the finite element, but actually computed) eigenvector in terms of the direct application of the Laplacian.
Comment by nilimanigam — September 14, 2012 @ 6:45 pm |
Here are some brief computations illustrating how an L^2 bound on the error in an approximate eigenfunction can be turned into L^infty bounds, at least if one is away from corners, thus avoiding the need to have to understand the residual.
More precisely, suppose that we have a true eigenfunction and some discretised approximation
and some discretised approximation 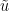 to this eigenfunction, and that we have somehow obtained a bound
to this eigenfunction, and that we have somehow obtained a bound 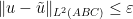 on the L^2 error (e.g. we should be able to get this if the Rayleigh quotient of
on the L^2 error (e.g. we should be able to get this if the Rayleigh quotient of 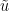 is close to the minimum value of
is close to the minimum value of  ).
).
Now suppose that the triangle ABC contains the disk for some radius R. A bit of messing around with polar coordinates shows that the function
for some radius R. A bit of messing around with polar coordinates shows that the function
is smooth on![[0,R]](https://s0.wp.com/latex.php?latex=%5B0%2CR%5D&bg=ffffff&fg=000000&s=0&c=20201002) , equal to
, equal to 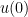 at the origin, and obeys the Bessel differential equation
at the origin, and obeys the Bessel differential equation 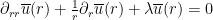
which can be solved using Bessel functions as
thus
for all . Integrating this against a test function
. Integrating this against a test function  we get
we get
Splitting into
into 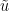 and
and  and using Cauchy-Schwarz to bound the latter term, we obtain
and using Cauchy-Schwarz to bound the latter term, we obtain
This gives a computable upper and lower bound for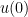 . From the Cauchy-Schwarz inequality, we see that the optimal value of
. From the Cauchy-Schwarz inequality, we see that the optimal value of  here is
here is  , leading to the bound
, leading to the bound
where
Of course, this estimate works best when R is large, and we can only fit a big ball B(0,R) inside the triangle ABC if the origin 0 is deep in the interior of ABC. But if instead 0 is near an edge of ABC, but far from the vertices, one can still get a big ball inside the domain after reflecting the triangle across the edge 0 is near (but this multiplies the L^2 norm of the residual by a factor of sqrt(2)). In principle, this gives L^infty control on u everywhere except near the corners. (Of course, one still has to numerically integrate the expressions in (1) and (2), but this looks doable, albeit messy.)
Comment by Terence Tao — September 20, 2012 @ 10:42 pm |
This is really useful!
Here’s how I was trying to proceed:
Suppose u is the exact eigenfunction, and its exact projection onto the finite dimensional subspace
its exact projection onto the finite dimensional subspace 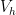 . I was trying to compute the precise asymptotic constant
. I was trying to compute the precise asymptotic constant  in the sup-norm estimate
in the sup-norm estimate  (this is the kind of FEM estimate one gets, eg. page 3 of http://people.math.sfu.ca/~nigam/polymath-figures/Validation+Numerics.pdf), but I think your argument above may help with this.
(this is the kind of FEM estimate one gets, eg. page 3 of http://people.math.sfu.ca/~nigam/polymath-figures/Validation+Numerics.pdf), but I think your argument above may help with this.
One then has to estimate , where both now live in
, where both now live in 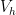 . I think this can be controlled using the inverse and backward error estimates for eigenvalue problems – the trick is getting the asymptotic constants decently. One then puts these estimates together
. I think this can be controlled using the inverse and backward error estimates for eigenvalue problems – the trick is getting the asymptotic constants decently. One then puts these estimates together
I’m also (still!) trying to debug the code to locate the extrema of the piecewise quadratics on the smaller triangles. This would circumvent the interpolation-to-linears step. The calculations are so very messy (not hard), so I’m going very slowly.
Comment by Nilima Nigam — September 21, 2012 @ 6:13 pm |
I’ve been mulling over sup-norm error estimates for the eigenfunctions. I’ve looked through the literature and spoken to some people; apparently, there are no a posteriori sup-norm estimates for eigenfunctions. In other words, if I compute a finite element approximation to an exact eigenfunction, there are (at present) no error bounds (in sup norm) in terms of the computed quantity. There are estimates in terms of the exact eigenfunction (a priori estimates), but since one doesn’t have the exact eigenfunction at hand, the kind of control we want is not readily available.
In other news, I’ve started to play around with an interval arithmetic software, to move towards a validated numerics approach. I can now check the quality of a Lanczos approximation to a discrete eigenvector, but the interval sizes grow with the size of the discrete linear system. In other words, as one gets a better FEM approximation, the quality of the interval arithmetic bounds on the discrete approximant get poor. All of this is an attempt to get some handle on item (5) in the summary above. It would be very helpful to have an expert in interval arithmetic.
I will try to write this up in some notes over the next few days.
Comment by Nilima — July 12, 2013 @ 8:49 pm |
Glad to hear that this project isn’t completely dead :). If rigorous sup-norm estimates for eigenfunctions are not in the literature, then this could be an interesting objective for us to pursue, as it could end up being useful for other things than the hot spots conjecture for acute triangles.
Comment by Terence Tao — July 12, 2013 @ 9:28 pm |
This project is very interesting, at least for me. The finite element method, and how we usually analyze it, is very much in a variational (weak) spirit; questions of how one solves the resultant discrete systems are usually considered as a distinct, unrelated problem. The hot spots conjecture is merciless in the sense that all aspects of approximation have to be simultaneously controlled.
I agree- developing rigorous a posteriori sup-norm estimates for eigenfunctions would be useful beyond the Hot Spots conjecture. Similar estimates for solutions of elliptic PDE, and most likely the approaches used there could be modified.
Comment by nilimanigam — July 12, 2013 @ 9:44 pm |
For a result of this type in a related context (eigenfunctions on congruence hyperbolic surfaces, i.e. periodic boundary conditions) see the paper of Booker–Strombergsson–Venkatesh. The difficulties there have to do with the non-compactness of the surface, but the numerics provide an approximation as a sum of a sequence of (individually non-periodic) eigenfunctions.
Comment by Lior Silberman — July 13, 2013 @ 3:00 am |
Thank you for the reference! The approach used in this reference is rather different from a finite element strategy. It would certainly be good if these results can be applied to the hot spots problem on acute triangles. This would represent a different approach to the approximation strategy I’m trying.
Comment by nilimanigam — July 13, 2013 @ 3:58 am
Here is a variant my Sep 20 10:42 comment for converting L^2 error estimates on an error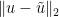 of an eigenfunction into sup-norm estimates, now in a neighbourhood of one vertex rather than in a ball. Namely, suppose that the triangle ABC contains a sector
of an eigenfunction into sup-norm estimates, now in a neighbourhood of one vertex rather than in a ball. Namely, suppose that the triangle ABC contains a sector  around one vertex A of the triangle (so A is the origin, AB is horizontal, and AC rises at an angle
around one vertex A of the triangle (so A is the origin, AB is horizontal, and AC rises at an angle  ). Suppose that the true eigenvalue
). Suppose that the true eigenvalue  to the true eigenfunction
to the true eigenfunction  is known (this is an oversimplification, but in practice we should be able to get reasonably good upper and lower bounds on this quantity). Then the eigenfunction
is known (this is an oversimplification, but in practice we should be able to get reasonably good upper and lower bounds on this quantity). Then the eigenfunction  in this sector must take the form
in this sector must take the form
for some coefficients which we do not currently know. However, from the regularity theory (see wiki) we have the H^3 estimate
which we do not currently know. However, from the regularity theory (see wiki) we have the H^3 estimate
which by the Bessel function expansion and orthogonality in the angular variable leads to an inequality of the form
where the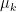 are the explicitly computable expressions
are the explicitly computable expressions
which, thanks to the triple derivative, should grow like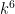 . This allows us to obtain pointwise (or sup norm) estimates for the error between
. This allows us to obtain pointwise (or sup norm) estimates for the error between 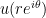 and a truncated Bessel expansion
and a truncated Bessel expansion
indeed the error can be bounded using the Cauchy-Schwarz inequality and (1) by
can be bounded using the Cauchy-Schwarz inequality and (1) by
which is a quantity that decays like , which is a respectable rate of convergence (and there is a chance that one can do a bit more integration by parts to get even more regularity than H^3 which would lead to faster convergence here).
, which is a respectable rate of convergence (and there is a chance that one can do a bit more integration by parts to get even more regularity than H^3 which would lead to faster convergence here).
Next, one has to estimate the coefficients . But from orthogonality in the angular variable we have
. But from orthogonality in the angular variable we have
for any test function , one can then compute approximants
, one can then compute approximants
to each coefficient and use Cauchy-Schwarz to control the error
and use Cauchy-Schwarz to control the error  in terms of
in terms of 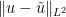 (indeed, Fourier orthogonality in the angular variables allows one to control the error
(indeed, Fourier orthogonality in the angular variables allows one to control the error  ), and as before one can choose the
), and as before one can choose the  to optimise the Cauchy-Schwarz calculation.
to optimise the Cauchy-Schwarz calculation.
In principle, this all gives sup-norm control on the true eigenfunction in a neighbourhood of a vertex. When one is very close to the vertex there is an added bonus that all but the zero mode Bessel function decays, and so one should also be able to get enough control to verify the hot spots conjecture very close to the vertex.
Comment by Terence Tao — July 13, 2013 @ 12:19 am |
This is helpful.
Let me see if I understand the implication.
First, if one can conclude (analytically or numerically) that the extrema of the true eigenfunction lie sufficiently close to vertices, then the argument above provides explicit control on where the extremum must occur.
Next, if one can conclude that an approximation to the true eigenfunction is close in the sup norm, and that the extrema of the approximant are close to vertices, then one can use a combination of an error estimate and the argument above to conclude the result.
Last year I tried to use approximations which consisted of truncated Bessel expansions around all three vertices simultaneously, to compute the eigenfunction. This worked reasonably, but there is no proof that the strategy I attempted is a convergent one.
Comment by nilimanigam — July 13, 2013 @ 1:10 am |
Yes, this is basically right. Actually, one can cover an acute triangle by three sectors (each of which is centred at one vertex and just touches the opposite edge) so in principle if we get a good enough approximation in each of the three sectors, we can pin down exactly where the extrema occur.
If the extremum is numerically observed to occur in a vertex, then what should happen is that near the vertex, the zero mode will dominate and we can use the above bounds to show that there is no local extremum near that vertex other than at the vertex itself, and hopefully when one is a bit further away from the vertex one has enough control on the other coefficients
will dominate and we can use the above bounds to show that there is no local extremum near that vertex other than at the vertex itself, and hopefully when one is a bit further away from the vertex one has enough control on the other coefficients 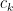 as well that one can show that one is smaller than at the global extremum.
as well that one can show that one is smaller than at the global extremum.
A trickier situation is when the extremum is numerically observed to occur on an edge but not on a vertex (but maybe this situation never occurs? I can’t remember what the numerics suggested here). Sup-norm estimates can then show that the true extremum must be close in location to the numerical extremum, but to place the true extremum exactly on the edge rather than near it, we need something like a lower bound on the second derivative of u in the normal direction (because if one has an extremum at some point P near an edge, with Neumann boundary conditions, then the normal first derivative of u vanishes both on the edge and at P and so by the intermediate value theorem the second derivative in the normal direction vanishes somewhere between P and the edge). This will require some additional argument (the H^3 control given above, by Sobolev embedding, would give uniform control on first derivatives but not on second), or perhaps there is another way to force extrema to lie on the edge that do not require second derivative control.
Comment by Terence Tao — July 13, 2013 @ 1:46 am |
In the tricky situation you describe, do we need uniform estimates? Or only something local, near the problematic point P? The estimates would depend on the distance to the edge, but does one need high regularity right upto the boundary for such an argument?
Is there a length scale we can identify from the argument above?
Close to a vertex, as you point out the dominant behaviour of the true eigenfunction is that of a Bessel J_0. The length scale over which it dominates must go as the square root of the eigenvalue. Or is there some other asymptotic scaling?
The eigenvalue of interest is not small. So if one computes an approximation that’s finer than this length scale, has the requisite a posteriori estimates, and checks that the extrema of the approximants are at the vertex, then that should be good enough to conclude the result.
Numerically, for all the triangles tested, the extrema of piecewise linear approximants (or projections of piecewise quadratics onto a finer space of linears) always and unambiguously lie on a vertex.
Comment by nilimanigam — July 13, 2013 @ 2:12 am
We would only need local estimates (since away from P sup norm estimates should suffice), but given that the numerics indicate that the extremum always occurs on a vertex, maybe we don’t need to worry about this situation as it looks like it doesn’t actually exist.
One can get a sense of when the zeroth term dominates by pretending that only the zeroth and first mode appear:
Let’s say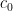 is positive, so that
is positive, so that  has a local maximum at the origin. Then we cannot beat this maximum whenever
has a local maximum at the origin. Then we cannot beat this maximum whenever
For small r we have and
and  , so we can control the region in which
, so we can control the region in which
or
So, yes, the scale is basically , but one also needs to know the ratio between
, but one also needs to know the ratio between 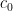 and
and  .
.
Comment by Terence Tao — July 13, 2013 @ 2:43 am
This thread is now looking very similar to the computations for hyperbolic surfaces using the Whittaker expansion. Has the following algorithm been tried? (analogue of the “collocation method” from the hyperbolic surface with periodic boundary conditions):
Fix a large integer K and a (putative) eigenvalue . Now for
. Now for  let
let 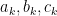 be coefficients that will be taken to be variables. In each of the three sectors defined by Terry (the with center at a vertex and tangent to the opposite edge), consider the finite expansion in Bessel functions with the relevant coefficients.
be coefficients that will be taken to be variables. In each of the three sectors defined by Terry (the with center at a vertex and tangent to the opposite edge), consider the finite expansion in Bessel functions with the relevant coefficients.
Now let be some other (larger) integer parmeter). For
be some other (larger) integer parmeter). For  points
points 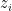 which are in the intersection of at least two sectors, the statement “the two expansions agree at
which are in the intersection of at least two sectors, the statement “the two expansions agree at 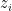 is a linear equation in the unknown coefficients.
is a linear equation in the unknown coefficients.
Finally, take large enough that the system is over-determined, find the least-squares solution. Then its goodness-of-fit is an evaluation of how close we are to an eigenfunction.
large enough that the system is over-determined, find the least-squares solution. Then its goodness-of-fit is an evaluation of how close we are to an eigenfunction.
Relation to a-posteriori estimates:
1. You can make an a-priori estimate on the truncation length needed for a given sup-norm bound in the rectangle.
needed for a given sup-norm bound in the rectangle. which minimize the
which minimize the 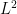 norm of the normal derivative at the opposite edge]
norm of the normal derivative at the opposite edge]
2. The formal expansions with the guessed parameters are in facts exact eigenfunctions of the Laplacian in the plane; the only question is whether they satisfy the boundary conditions at the “missing edge”, which can be tested [in fact, that is an alternative approach: find the coefficients
3. I wonder if the approach of Booker–Strombergsson–Venkatesh can also be used here to “validate” an approximate eigenfunction however it is first found.
Comment by Lior Silberman — July 13, 2013 @ 7:14 am
Lior, we’ve tried something analogous to what you suggest – it’s a variant of the Betcke-Trefethen approach, which in turn stabilizes the classical ‘Method of Particular Solutions’ by Fox, Henrici and Moler.
Click to access NA-03-12.pdf
Here’s the approach I used: where
where  are Bessel-Fourier functions which are individually eigenfunctions. Enforce that the linear combination has zero normal derivative at the boundary. Augment the system by enforcing that the eigenfunctions are not zero at a random number of points in the interior. Perform a QR decomposition of the resultant system, throw away the rows which correspond to the augmented conditions, look for the minimal singular value of the remaining Q. Sweep through a range of frequencies to get the one which makes this minimal singular value zero.
are Bessel-Fourier functions which are individually eigenfunctions. Enforce that the linear combination has zero normal derivative at the boundary. Augment the system by enforcing that the eigenfunctions are not zero at a random number of points in the interior. Perform a QR decomposition of the resultant system, throw away the rows which correspond to the augmented conditions, look for the minimal singular value of the remaining Q. Sweep through a range of frequencies to get the one which makes this minimal singular value zero.
Take an expansion of form
This works OK. There is no proof that I’m aware of that the algorithm is supposed to converge for the Neuman problem on Lipschitz domains. An error analysis of the QR +SVD step is also somewhat messy. In other words, this gives me approximate eigenvalues and eigenfunctions, but there are no theorems that this method is converging to the right result.
Here’s another tweak to the same idea, using an overlapping Schwarz iteration http://people.math.sfu.ca/~nigam/polymath-figures/Schwarz.pdf
If you have experience in using the method you suggested, it would great it could be given a try. It sounds perhaps like your variant is provably convergent?
Comment by nilimanigam — July 13, 2013 @ 3:01 pm
Lior: this is a nice approach! One side benefit of this approach (particularly if one constrains derivatives of the three sectorial solutions to match at various points, as well as the values themselves) is that if one forms approximate eigenfunctions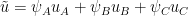 , where
, where  is a smoothish partition of unity to the three sectors that have vanishing normal derivative, and
is a smoothish partition of unity to the three sectors that have vanishing normal derivative, and  are the numerically obtained finite Bessel expansions around the three vertices
are the numerically obtained finite Bessel expansions around the three vertices 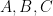 of the triangle, then (a)
of the triangle, then (a) 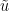 automatically obeys the Neumann condition, and (b) the residual
automatically obeys the Neumann condition, and (b) the residual  should be well controlled, which should automatically lead (via some spectral calculus and normalisation, combined with some lower bounds for the spectral gap
should be well controlled, which should automatically lead (via some spectral calculus and normalisation, combined with some lower bounds for the spectral gap 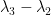 ) to good bounds on
) to good bounds on  and hence (by Sobolev embedding, for which we have explicit constants on the triangle) to sup norm estimates on
and hence (by Sobolev embedding, for which we have explicit constants on the triangle) to sup norm estimates on  (probably better than what I was proposing previously, particularly away from the vertices of the triangle, though we can use the other approach too when one is near the vertices). Indeed we have
(probably better than what I was proposing previously, particularly away from the vertices of the triangle, though we can use the other approach too when one is near the vertices). Indeed we have
and
and
so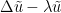 should be small if
should be small if 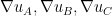 are close to agreeing on their common domains of definition, and similarly for
are close to agreeing on their common domains of definition, and similarly for  . There is the question of how to choose
. There is the question of how to choose 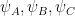 but perhaps a quadratic spline would already give decent results.
but perhaps a quadratic spline would already give decent results.
Comment by Terence Tao — July 13, 2013 @ 3:40 pm
This would be perhaps equivalent to an overlapping Schwarz method, where the overlap regions correspond to the places where two partition-of-unity-functions are both non-zero. Last September (comment 16?) I think we did try this, admittedly in an iterative manner. If there is a way to get the eigenvalue and eigenfunction in one shot, and the numerical strategy is provably convergent, that would be very nice!
Comment by nilimanigam — July 13, 2013 @ 4:08 pm
Actually, another approach to rigorous error estimates just occurred to me: if one takes the Bessel function expansions of the true eigenfunction around each vertex
around each vertex 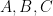 and truncates them, then one obtains a competitor to the numerically obtained truncated Bessel expansions in either Lior or Nilima’s least squares problem, and one should be able to obtain a rigorous estimate as to how small the least squares quantity is for this competitor. If this least squares problem has a good spectral gap (which is a numerically computable quantity), one would have a good, rigorous, and numerically computable, error bound for how the truncated true Bessel coefficients differ from the numerically obtained truncated Bessel coefficients (more precisely, we would have rigorously placed the first
and truncates them, then one obtains a competitor to the numerically obtained truncated Bessel expansions in either Lior or Nilima’s least squares problem, and one should be able to obtain a rigorous estimate as to how small the least squares quantity is for this competitor. If this least squares problem has a good spectral gap (which is a numerically computable quantity), one would have a good, rigorous, and numerically computable, error bound for how the truncated true Bessel coefficients differ from the numerically obtained truncated Bessel coefficients (more precisely, we would have rigorously placed the first  true Bessel coefficients of each vertex in a certain numerically computable ellipsoid). This type of control, combined with the decay estimates for the coefficients beyond the first
true Bessel coefficients of each vertex in a certain numerically computable ellipsoid). This type of control, combined with the decay estimates for the coefficients beyond the first  , should in principle be enough to verify a hypothesis that the extrema of the true eigenfunction only occur at vertices.
, should in principle be enough to verify a hypothesis that the extrema of the true eigenfunction only occur at vertices.
ADDED LATER: Doing an abrupt truncation of the Bessel series expansion to the first K coefficients amounts to performing a Dirichlet Fourier series summation of the true eigenfunction (restricted to a sector) in the angular variable. It may be that a smoother truncation (e.g. corresponding to a Fejer Fourier series summation) gives superior results. On the other hand, the variety of truncations available suggests that we in fact do not have a good spectral gap (at least with respect to the higher modes), but perhaps we still get good control on the low frequency Bessel modes, which are the most crucial for us…
Comment by Terence Tao — July 13, 2013 @ 4:10 pm
I apologize, I need to proceed slowly before I try to code up what I understand of Lior’s suggestion. Let the three angles of the triangle be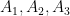 , and denote for convenience
, and denote for convenience  Let
Let  be
be 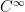 functions such that
functions such that 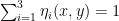 for each point in the triangle,
for each point in the triangle,  in a sectorial domain of radius
in a sectorial domain of radius  centered at vertex
centered at vertex  .
.
We want to find unknown constants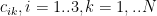 and an approximate eigenvalue
and an approximate eigenvalue  such that
such that  is an approximate eigenfunction. Here
is an approximate eigenfunction. Here  are, in polar coordinates, the distances of the point
are, in polar coordinates, the distances of the point  from each of the vertices.
from each of the vertices.
To find , we build an overdetermined system. First we place
, we build an overdetermined system. First we place  points on the boundary of the triangle, and require that the normal derivative of
points on the boundary of the triangle, and require that the normal derivative of 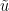 vanishes at these points. Next we place, at random,
vanishes at these points. Next we place, at random, 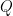 points in the overlap domains and demand that
points in the overlap domains and demand that 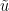 at these points is not identically zero. Specifying these gives us a matrix
at these points is not identically zero. Specifying these gives us a matrix  , where
, where  has zeros at the entries corresponding to boundary points.
has zeros at the entries corresponding to boundary points. which makes the minimal singular value of
which makes the minimal singular value of 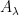 to be zero. With the additional Q points, we either have to solve the (nonlinear) overdetermined system, or use a strategy like the Timo-Betcke one.
to be zero. With the additional Q points, we either have to solve the (nonlinear) overdetermined system, or use a strategy like the Timo-Betcke one.
If one had not added the additional Q points, looking for the unknown coefficients and eigenvalue is equivalent to looking for a
Lior, is this what you were suggesting?
Comment by nilimanigam — July 13, 2013 @ 4:38 pm
Not quite. I combined my numerical scheme with Terry’s post-solution construction into a PDF which I posted here.
Comment by Lior Silberman — July 13, 2013 @ 7:26 pm
Lior, I have two questions.
1. On the first page of your notes, the equivalence statement (relating the expressions around vertices j and j+1): is the claim that for point in these overlap regions, the true eigenfunction is well-expressed as Bessel-trig functions expanded around either the vertex j or the vertex j+1, and therefore these expansions can be set equal? When I am stuck now, and have been before while attempting either the overlapping Schwarz idea or something else using Bessel-trig functions, is the same choice of ‘K’ on both sides for the truncated expansions being used. Near the corners these expansions are great. Away from them, the projection of the true eigenfunction onto an finite expansion around any given vertex may or may not converge fast.
2. Section 3. I’m not familiar with the BSV idea and read the paper only this morning. I don’t see why the computed coefficients have to be e-accurate in general.
I agree with how to check that a given approximate eigenfunction is a good one.
Comment by nilimanigam — July 13, 2013 @ 8:17 pm
Good points.
1. You’re right — the eigenfunction does not have to be smooth at the boundary, only in the interior. Perhaps we need to reduce the radius of the sectors a little. We need to make an estimate to check the cutoff. I will try estimating the decay rate of the a_k.
2. I’m not familiar with the details of B–S–V either — I was just making a very vague suggestion. But if it works it gives sup-norm bounds. The one thing I understand is that it works _if_ the computed coefficients are good. It’s not a method for obtaining good approximations, but rather of showing that a numerically computed approximation is good if it happens to be so.
Comment by Lior Silberman — July 13, 2013 @ 11:34 pm
So unfortunately, nothing we discussed panned out. But the following were some ideas considered:
1) Perhaps it is the case that the nodal line is the image of a line or circle (hyberbolic geodesic?) under the Schwarz–Christoffel mapping. Or if not the image then close to it. Bartlomiej made some computer simulations and in many cases the fit was very close but for the equilateral triangle the fit was a fair bit off.
2) Terry’s re-proof of a coupling-argument using the vector maximum principle begs the question: Is it possible to reprove the Hot-Spots conjecture for obtuse triangles (the paper of Banuelos and Burdzy) using such a non-probabilistic argument? If so, perhaps the proof could be extended to the non-obtuse case. Of course we can see by computer simulation that the gradient field of certain acute triangles is much nastier… but I think it is still the case that the gradient vectors all lie in a half space? In fact I think the hot-spots conjecture would hold if we could show that the gradient vectors all lie in a (non-convex) cone of angle less than 360 degrees. In summary: Maybe something can be said about the gradient field.
3) There suggestion of Mihai Pascu involving the nodal line dividing the triangle into star-like domains with respect to hyperbolic geodesics. But I didn’t quite follow/remember… maybe Barlomiej can better explain.
4) There was the suggestion of Baneulos that we might examine the function where
where 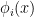 is the
is the  -th Dirichlet eigenfunction of the triangle. Apparently this ratio has properties similar to the second Neumann eigenfunction.
-th Dirichlet eigenfunction of the triangle. Apparently this ratio has properties similar to the second Neumann eigenfunction.
That’s all I can remember… hopefully I didn’t miss any.
Edit: I remembered another interesting comment:
5) Chris Burdzy pointed out that any argument used has to be one that wouldn’t work on a manifold. He gave the following counter-example: Consider the surface of a long baguette. The hot spots would then be at the
tips of the baguette”. This is a manifold without boundary but then you can cut a small hole in the baguette to make the surface into a manifold with boundary. If the hole is small enough, the hot spots wouldn’t move much and would therefore not be on the boundary.
Comment by Chris Evans — September 16, 2012 @ 10:56 pm |
The observation (1) is interesting! let’s ignore the equilateral triangle case for the time being: is the nodal line always a line/circle under the Schwarz-Christoffel map? Is there some simple way to see this?
Comment by Nilima Nigam — September 17, 2012 @ 10:02 pm |
Presumably one can do explicit calculations for the 45-45-90 triangle. If the vertices are (0,0), (1,0), (1,1) then the second eigenfunction is and the nodal line is the bisecting altitude connecting (1/2,1/2) with (1,0). I guess this transforms to a horocycle or something under Schwarz-Christoffel?
and the nodal line is the bisecting altitude connecting (1/2,1/2) with (1,0). I guess this transforms to a horocycle or something under Schwarz-Christoffel?
The other explicit example is the 30-60-90 triangle, but the nodal line there is a bit more complicated. If we use the triangle with vertices (0,0,0), (1,-1,0), (1,-1/2,-1/2), the second eigenfunction is , and I can’t work out the nodal line for that in my head…
, and I can’t work out the nodal line for that in my head…
Comment by Terence Tao — September 17, 2012 @ 10:44 pm |
Bartlomiej’s numerical simulations suggested conjecture (1) was false for equilateral triangles but true (or perhaps just coincidentally close) for the 30-60-90 triangle. As the 30-60-90 triangle is half the equilateral triangle perhaps there is a nice analytic way to compare the images of lines/circles under the SC-map for the two regions.
More specifically, does it hold that the image-of-lines/circles for the equilateral triangle are the reflections of those for the 30-60-90 triangle?
As a separate question: Suppose we could show that the nodal line lies in some specific “epsilon band”. That begs the question of how to prove a claim such as the following:
Claim: Consider an “almost-arc” with two straight Neumann-sides meeting at an acute angle at the corner and one wiggly Dirichlet-side such that the distance from any point of the Dirichlet-side to the corner
and one wiggly Dirichlet-side such that the distance from any point of the Dirichlet-side to the corner  lies in the interval
lies in the interval  . Then for suitably large
. Then for suitably large  and small
and small  , the maximum of the first eigenfunction should occur at the corner
, the maximum of the first eigenfunction should occur at the corner  .
.
(Instead of taking an “epsilon band” around a curved arc we might also take one around a straight line and consider an “almost-triangle”)
Our proofs using coupled-BM/vector-valued maximum principle won’t work if the Dirichlet-side is wiggly and yet intuitively the claim still ought to hold. Of course if it should hold by continuity, but it ought to hold for
it should hold by continuity, but it ought to hold for  not too small…
not too small…
Comment by Chris Evans — September 18, 2012 @ 4:39 pm |
I’ve been playing around a bit trying to estimate the in Terry’s notes, in particular the
in Terry’s notes, in particular the  term, where
term, where  denotes the area of the triangle. I scanned in some notes at
denotes the area of the triangle. I scanned in some notes at
Click to access Oct26th.pdf
Looking at the graph of the function in Wolfram Alpha it seems that and its first and second derivatives will blow up when
and its first and second derivatives will blow up when  is close to
is close to  … but that is old news I suppose and we can presumably handle the case where one of the angles is close to
… but that is old news I suppose and we can presumably handle the case where one of the angles is close to  by other means.
by other means.
Despite its nice structure I didn’t see an easy way to read off the eigenvalues/vectors of the Hessian of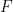 … but such information would yield a bound. In fact, using that our perturbation is restricted to a plane might give us a better bound.
… but such information would yield a bound. In fact, using that our perturbation is restricted to a plane might give us a better bound.
Comment by Chris Evans — October 26, 2012 @ 8:59 pm |
I want to preface this comment by saying that I have not read all of the comments in this and the previous threads, and I do not understand a large part of the arguments presented. However, I have read the wiki and I think I have a novel approach, which (for fear of sounding naive and stupid) may be simpler as well.
Would it perhaps be easier to prove the existence of a functor which takes right or obtuse triangles to acute triangles, and heat equations in the former triangle to heat equations in the latter? I’m not sure if this will work technically, but this homotopy-ish approach seems a lot more intuitive to me.
Once again, I really know nothing, I just couldn’t resist incase this was overlooked and could be useful.
Comment by Curley's Wife — June 18, 2013 @ 9:26 pm |
It’s not a bad suggestion, especially since harmonic functions are preserved under conformal mapping, and we have the Riemann mapping theorem that lets us conformally map any triangle to any other triangle. Unfortunately, conformal mappings do not preserve Laplacian eigenfunctions; the Laplacian is a function of the metric, and basically the only maps that preserve eigenfunctions are either isometries or similarities. In particular one cannot transform an acute angled triangle to be obtuse this way. (But we did get some mileage out of seeing what happens when one continuously deforms the angle and see how the eigenvalues transform.)
Comment by Terence Tao — June 19, 2013 @ 2:54 am |
I’ve attempted a summary of Bessel-Fourier approximation approaches presented on this project so far, at http://people.math.sfu.ca/~nigam/polymath-figures/summary.pdf I’ll post this to the Wiki a bit later, so we (I) keep track.
Comment by nilimanigam — July 13, 2013 @ 9:39 pm |
Great. I have updated my PDF with an a-priori estimate for the truncation. It depends on the geometrical fact (which I hope is true) that you can cover the triangle with subsectors which are slightly smaller than the full sectors we considered so far.
A few typos: Section 1 should have , equation (21) should have
, equation (21) should have  after the second equality. After the equation set
after the second equality. After the equation set 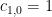 and not as written.
and not as written.
Comment by Lior Silberman — July 14, 2013 @ 12:54 am |
Thanks for the edits! I’ll clean up the notes.
Comment by nilimanigam — July 14, 2013 @ 1:29 am |
Here’s an explanation of the geometrical fact that one can cover the triangle by three sectors. Given a triangle , let
, let 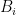 be the foot of the altitude from
be the foot of the altitude from 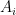 to
to  , thus the three altitudes
, thus the three altitudes  meet at the orthocentre
meet at the orthocentre  of the triangle, which is inside the triangle because it is acute. Because the sides of a right-angled triangle are less than the hypotenuse, we see that
of the triangle, which is inside the triangle because it is acute. Because the sides of a right-angled triangle are less than the hypotenuse, we see that 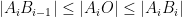 and similarly
and similarly 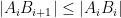 . Thus the sector
. Thus the sector 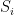 with apex
with apex 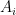 and radius
and radius  and tangent to
and tangent to  contains both the triangle
contains both the triangle  and
and  , and so the three sectors cover the entire triangle (with a bit of room to spare; for instance, the sectors only need to stretch to the orthocentre to cover everything. I think the circumcentre also works).
, and so the three sectors cover the entire triangle (with a bit of room to spare; for instance, the sectors only need to stretch to the orthocentre to cover everything. I think the circumcentre also works).
Incidentally it is possible to use reflection across to enlarge the sectors
to enlarge the sectors 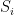 a little bit beyond the edge
a little bit beyond the edge  , but at the cost of worsening some of the error estimates by a factor of two or so (or more if one tries to use multiple reflections). But one should certainly avoid trying to stretch a Bessel expansion from one vertex
, but at the cost of worsening some of the error estimates by a factor of two or so (or more if one tries to use multiple reflections). But one should certainly avoid trying to stretch a Bessel expansion from one vertex 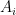 all the way to another vertex
all the way to another vertex 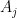 . If the angle at
. If the angle at 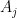 does not divide evenly into
does not divide evenly into  , then the eigenfunction will not be smooth at that point, and so the convergence of the Bessel expansion from
, then the eigenfunction will not be smooth at that point, and so the convergence of the Bessel expansion from 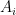 will be somewhat slow. (This makes it a bit remarkable that Nilima’s scheme has been giving such good results, it must somehow be relying on the overdetermined nature of the triple Bessel basis to somehow interpolate between the three true Bessel expansions in a way that I don’t currently understand.)
will be somewhat slow. (This makes it a bit remarkable that Nilima’s scheme has been giving such good results, it must somehow be relying on the overdetermined nature of the triple Bessel basis to somehow interpolate between the three true Bessel expansions in a way that I don’t currently understand.)
Comment by Terence Tao — July 14, 2013 @ 3:34 am |
I should hasten to clarify: the accuracy I’ve reported in comment (7) below is based on finite element calculation, approximating by piecewise polynomials. This approach uses basis functions whose support is local. The quality of the approximation/interpolant only depends on the smoothness of the eigenfunction. It doesn’t depend on the eigenfunction being well-expressed by Fourier-Bessel functions.
The FEM approximation to the eigenfunction looks like
 where the
where the  are piecewise polynomials, and each vanishes outside a specific simplex. Unlike the matrix using Fourier-Bessel or other approximants, the system one obtains for
are piecewise polynomials, and each vanishes outside a specific simplex. Unlike the matrix using Fourier-Bessel or other approximants, the system one obtains for 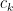 is very sparse. There is less ‘mixing’ of basis functions. I’m not articulating this well.
is very sparse. There is less ‘mixing’ of basis functions. I’m not articulating this well.
If the eigenfunction were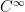 , then one could get a more efficient approximation using a spectral basis (like the Fourier-Bessel functions). The FEM work really well in situations of poorer regularity (we have
, then one could get a more efficient approximation using a spectral basis (like the Fourier-Bessel functions). The FEM work really well in situations of poorer regularity (we have  ).
).
I’d abandoned the use of spectral methods or Fourier-Bessel basis functions to approximate the eigenfunctions for two reasons:
(A) I had no guarantee that the method of particular solutions I was using, Section 2 of the notes attached, was convergent in this setting
Click to access summary.pdf
(B) the location of the eigenvalues was not easy to do.
The problem (b) arises when trying to find a value of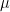 which would make the minimal singular value
which would make the minimal singular value  of a certain matrix to be zero. Locating the zeros of
of a certain matrix to be zero. Locating the zeros of
 proved very difficult since the functions were quite flat. The root-finding could not be done without yet another level of approximation.
proved very difficult since the functions were quite flat. The root-finding could not be done without yet another level of approximation.
Comment by nilimanigam — July 14, 2013 @ 3:55 am |
Ah, OK, thanks for the clarification! (I had misunderstood your July 13 3:01pm comment somewhat in this regard.)
Comment by Terence Tao — July 14, 2013 @ 4:14 am |
I just worked it out too; the truncation estimates work better with smaller sectors, so I’m tempted to use the sectors right up to the orthocentre. This set of sectors has relatively small intersections, which may be good (it means the error in the spectral estimate comes from a smaller subset of the triangle, where we can sprinkle our test points more densely) or may be bad (not enough interaction between our solutions in the sectors). The PDF is now updated with this, and also with an explicit bound on the Bessel function giving an explicit truncation estimate, using the a-priori supremum bound on the eigenfunction.
Comment by Lior Silberman — July 14, 2013 @ 7:59 am |
Sounds good! I couldn’t find a link to the updated notes though: http://www.math.ubc.ca/~lior/work/notes/HotSpotsNumerics.pdf seems to point to an older version.
Smaller sectors do indeed seem to lead to better truncation estimates: if a Bessel expansion has good control in a sector of radius R and angle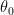 , then in a smaller sector of radius
, then in a smaller sector of radius 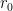 one should start getting exponential decay in the terms of the expansion once
one should start getting exponential decay in the terms of the expansion once  exceeds
exceeds  . But one needs a little bit of overlap between the sectors in order have the partition of unity that guarantees that solutions to the least squares problem are close to true eigenfunctions, although now that I think about it we don’t actually need this latter claim to be proven theoretically for our project, it is enough for this claim to be true empirically. We might experiment numerically with some different types of sectors to see what works best.
. But one needs a little bit of overlap between the sectors in order have the partition of unity that guarantees that solutions to the least squares problem are close to true eigenfunctions, although now that I think about it we don’t actually need this latter claim to be proven theoretically for our project, it is enough for this claim to be true empirically. We might experiment numerically with some different types of sectors to see what works best.
Another small comment: rather than pick some random points in the overlap between sectors and compare the distance between them, we could instead compute the L^2 norm of the difference on the overlapping region; this can be computed more or less exactly by first precomputing to high accuracy the inner product between two different Bessel basis functions on these overlapping regions to obtain the coefficients for the quadratic form between the coefficients that exhibits this L^2 norm. The reason for doing things this way is that then the rigorous error analysis only requires L^2 estimates on the truncation error rather than sup norm estimates, which may lead to some better estimation (avoiding the use of Sobolev). But then one needs the overlapping regions to have relatively large measure, so one can’t contract all the way to the orthocentre any more.
Another nice thing about this strategy is it might also handle Step 7 of the blog post as well as Steps 4-6 (actually it replaces Step 4 with something a bit different), and may also be robust to errors in the eigenvalue. Namely, suppose we are working with a mesh triangle with an approximate eigenvalue
with an approximate eigenvalue 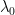 . Meanwhile, we consider a nearby triangle
. Meanwhile, we consider a nearby triangle 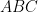 with a true eigenfunction
with a true eigenfunction  with true eigenvalue
with true eigenvalue  ; we do not consider
; we do not consider 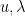 to be known (though we will need to somehow obtain a rigorous upper bound on the error
to be known (though we will need to somehow obtain a rigorous upper bound on the error  ), and the only thing we know about ABC is how close it is to
), and the only thing we know about ABC is how close it is to  . Then
. Then  has a Bessel expansion around each vertex, e.g. in polar coordinates around
has a Bessel expansion around each vertex, e.g. in polar coordinates around  it has an expansion of the form
it has an expansion of the form
where is the angle at
is the angle at  , and the coefficients
, and the coefficients 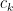 are currently unknown. This gives a candidate truncated Bessel expansion back in the reference triangle
are currently unknown. This gives a candidate truncated Bessel expansion back in the reference triangle  (or more precisely, in a sector of that triangle with vertex
(or more precisely, in a sector of that triangle with vertex 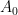 ):
):
where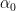 is the angle at
is the angle at 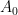 . (This is almost a distorted version of
. (This is almost a distorted version of  formed by rescaling the
formed by rescaling the  and
and  coordinates, except that the order of the Bessel function is also changing slightly.) Similarly we have Bessel expansions
coordinates, except that the order of the Bessel function is also changing slightly.) Similarly we have Bessel expansions  at the other two vertices of the reference triangle. Presumably if we take
at the other two vertices of the reference triangle. Presumably if we take  large enough,
large enough, 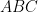 close enough to
close enough to  , and
, and  close enough to
close enough to 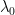 (with rigorous upper bounds on the error), we can rigorously prove error bounds (either in sup norm or maybe L^2 norm, as discussed above) on how the
(with rigorous upper bounds on the error), we can rigorously prove error bounds (either in sup norm or maybe L^2 norm, as discussed above) on how the  differ from each other in the overlapping region, so we get some bound on how well these coefficients perform in the least squares problem. Since we know the matrix coefficients in this least squares problem explicitly, we can numerically invert this and get some control on the true coefficients
differ from each other in the overlapping region, so we get some bound on how well these coefficients perform in the least squares problem. Since we know the matrix coefficients in this least squares problem explicitly, we can numerically invert this and get some control on the true coefficients  of the true eigenfunction around a given vertex (e.g. A), I think we get to place these coefficients in some ellipsoid (we may have to do some normalisation of the coefficients first to avoid the degenerate case when all the coefficients vanish). If we’re lucky, the ellipsoid is small enough that we can then rigorously show that within each sector, the true eigenfunction does not exceed the most extreme values on the three vertices, and then we would have shown the hot spots conjecture for all triangles sufficiently close to the reference triangle (skipping the step where we try to prove theoretical stability estimates for eigenfunctions with respect to deformation of the domain; the point is that we are going to rely on numerical stability instead of theoretical stability. In particular, we no longer need theoretical lower bounds on the spectral gap
of the true eigenfunction around a given vertex (e.g. A), I think we get to place these coefficients in some ellipsoid (we may have to do some normalisation of the coefficients first to avoid the degenerate case when all the coefficients vanish). If we’re lucky, the ellipsoid is small enough that we can then rigorously show that within each sector, the true eigenfunction does not exceed the most extreme values on the three vertices, and then we would have shown the hot spots conjecture for all triangles sufficiently close to the reference triangle (skipping the step where we try to prove theoretical stability estimates for eigenfunctions with respect to deformation of the domain; the point is that we are going to rely on numerical stability instead of theoretical stability. In particular, we no longer need theoretical lower bounds on the spectral gap 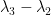 , although this gap will still need to be large in order for the least squares problem to be numerically stable).
, although this gap will still need to be large in order for the least squares problem to be numerically stable).
Comment by Terence Tao — July 14, 2013 @ 5:22 pm |
Sounds good!
There are two steps in this strategy whose numerical stability and conditioning one would need to establish. First: one has to solve the least squares problem to locate the coefficients in the expansion for a given guess of an eigenvalue (ie, the step of locating vector in Lior’s notes), and the quantity
in Lior’s notes), and the quantity 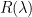 .
.
Next, one has to vary this guess of until
until 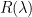 has a zero, which one then identifies as the eigenvalue. In essence, this is the location of the root of a nonlinear function.
has a zero, which one then identifies as the eigenvalue. In essence, this is the location of the root of a nonlinear function.
The size of the coefficient ellipsoid will depend on how well one can perform both these steps.
Comment by nilimanigam — July 14, 2013 @ 5:47 pm |
One can get theoretical upper bounds on by taking the Rayleigh quotient of a candidate eigenfunction; it doesn’t matter if there is no rigorous justification whatsoever as to whether the candidate eigenfunction is actually close to the true eigenfunction, it will always provide a rigorous upper bound. So one could use “illegal” methods to procure a candidate eigenfunction that one believes (but cannot prove) to be accurate, compute the Rayleigh quotient to produce a rigorous upper bound for
by taking the Rayleigh quotient of a candidate eigenfunction; it doesn’t matter if there is no rigorous justification whatsoever as to whether the candidate eigenfunction is actually close to the true eigenfunction, it will always provide a rigorous upper bound. So one could use “illegal” methods to procure a candidate eigenfunction that one believes (but cannot prove) to be accurate, compute the Rayleigh quotient to produce a rigorous upper bound for  , and then cross one’s fingers and hope that this is actually close enough to the true eigenvalue that we get numerical stability in the resulting least squares problem (which is something we can validate empirically, also we can compute
, and then cross one’s fingers and hope that this is actually close enough to the true eigenvalue that we get numerical stability in the resulting least squares problem (which is something we can validate empirically, also we can compute 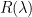 for additional reassurance).
for additional reassurance).
The Rayleigh quotient also gives rigorous comparison inequalities for the eigenvalue with respect to deforming the triangle, since the true eigenfunction for one triangle can be transformed (via an affine transformation) to a candidate eigenfunction for a nearby triangle. On the wiki it is noted that this argument gives
for the second eigenvalue of a triangle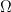 and an affine transform
and an affine transform 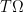 of that triangle. Thus the true eigenvalue of a nearby triangle is rigorously known to be close to the true eigenvalue of a reference triangle, and as mentioned above we can rigorously upper bound the true eigenvalue of the reference triangle by a Rayleigh quotient of some candidate eigenfunction for the reference triangle. The one thing that is missing is a rigorous lower bound for the true eigenvalue that comes close to matching the rigorous upper bound.
of that triangle. Thus the true eigenvalue of a nearby triangle is rigorously known to be close to the true eigenvalue of a reference triangle, and as mentioned above we can rigorously upper bound the true eigenvalue of the reference triangle by a Rayleigh quotient of some candidate eigenfunction for the reference triangle. The one thing that is missing is a rigorous lower bound for the true eigenvalue that comes close to matching the rigorous upper bound.
Comment by Terence Tao — July 14, 2013 @ 5:57 pm |
I’ll have to think about this a bit. For example, when one uses an approximation subspace that is not a strict subspace of $H^1$, one can get a numerical Rayleigh quotient which is lower than the true eigenvalue. I’m using this fact to get the ‘bracketing’ of eigenvalues, when I use P1 nonconforming and P1 conforming elements.
Your comment about the computed eigenvalue being the true eigenvalue of a nearby triangle is reminiscent of ‘backward error analysis’, and I should look up the results on these techniques for numerical eigensolvers.
Comment by nilimanigam — July 14, 2013 @ 6:03 pm |
I’m going to try to code up Lior’s approach. Lior, are you also coding? We can then compare.
Comment by nilimanigam — July 14, 2013 @ 6:15 pm |
Coding would be a few hours work, something I don’t really have. I’ll try finding an opportunity.
Comment by Lior Silberman — July 15, 2013 @ 2:14 am
I started to code, am hampered by lack of good bessel-function routines. Where can I get one?
I assume you already know this, but (as in my notes) I think it’s important to normalize the Bessel function as because otherwise as $\nu$ gets large there is exponential suppression which will make the Fourier coefficients artificially big for no reason and cause problems with precision. The analogous normalization is standard in the hyperbolic triangle calculations.
because otherwise as $\nu$ gets large there is exponential suppression which will make the Fourier coefficients artificially big for no reason and cause problems with precision. The analogous normalization is standard in the hyperbolic triangle calculations.
Comment by Lior Silberman — July 15, 2013 @ 3:51 pm
Copied the notes again to the website, should be OK now. I give explicit bounds on the exponential convergence in a subsector, from which sup-norm bounds on the truncation are not hard to get, but L^2-bounds ought to be possible too.
Comment by Lior Silberman — July 14, 2013 @ 9:18 pm |
Lior, what language or software are you using? The NAG library S17DEF is a good implementation in Fortran (there’s also a C version). Matlab uses a fairly reliable (MEXed version) of a library out of Sandia. As with all such things, care must be exercised as the order increases. I don’t blindly trust computed Bessel functions beyond order 20, one needs to order computations carefully in this instance.
I’m using the normalization of the Bessel functions you suggested.
Comment by nilimanigam — July 15, 2013 @ 9:28 pm |
I’ve got a very preliminary variant of the code ‘running’. It’s sensitive to the choice of points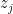 in the overlap regions. I will debug and test more tomorrow, but ideas on good choices of the
in the overlap regions. I will debug and test more tomorrow, but ideas on good choices of the 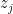 would be helpful.
would be helpful.
Terry, in your comment you mention the idea of precomputing the inner product between two Bessel basis functions in the overlap region of the two sectors. This may lead to a scheme which is less sensitive to choices of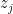 (if I understand correctly).
(if I understand correctly).
To be clear, if is the overlap between two sectorial regions centered at vertices i and j, do you mean one should precompute:
is the overlap between two sectorial regions centered at vertices i and j, do you mean one should precompute:
Comment by nilimanigam — July 14, 2013 @ 10:53 pm |
If the guess is far from an eigenvalue then you would expect sensitivity in the choice of
is far from an eigenvalue then you would expect sensitivity in the choice of 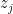 since there is no self-consistent solution anyway, but this isn’t a problem. If the scheme works at all then the sensitivity should go down as you near the eigenvalue.
since there is no self-consistent solution anyway, but this isn’t a problem. If the scheme works at all then the sensitivity should go down as you near the eigenvalue.
I would guess having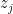 uniformly distributed in the intersection. If you take the sectors bounded by the orthocentre then the intersection of two wedges is divided by the end of the altitude from the opposite vertex; discretize this segment and then for each point discretize the horizontal segment at that height which is bounded by the ends of the wedges at both sides. Intuitively you want the number of
uniformly distributed in the intersection. If you take the sectors bounded by the orthocentre then the intersection of two wedges is divided by the end of the altitude from the opposite vertex; discretize this segment and then for each point discretize the horizontal segment at that height which is bounded by the ends of the wedges at both sides. Intuitively you want the number of 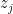 in a particular intersection proportional to the area of that intersection, but I’m not sure this level of detail is worth it.
in a particular intersection proportional to the area of that intersection, but I’m not sure this level of detail is worth it.
If you compute the inner product are proposed by Terry it should include the angular component, but note that rather than you should have
you should have 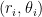 on both sides of the inner product since each expansion is centred at a different vertex.
on both sides of the inner product since each expansion is centred at a different vertex.
Comment by Lior Silberman — July 15, 2013 @ 12:09 am |
I currently take an equispaced set of points in a disk inside the intersection domain, fix the set, and then try to find the which minimizes
which minimizes 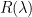 . The shape of this
. The shape of this 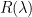 function seems to vary depending on where I put this set of points.
function seems to vary depending on where I put this set of points.
I’ll try what you suggest, but it would be very helpful if we could compare code or numerical results.
Thanks – I’m indeed using the with distances computed from the appropriate vertex, when it’s in the argument of the basis function around that vertex.
with distances computed from the appropriate vertex, when it’s in the argument of the basis function around that vertex.
Comment by nilimanigam — July 15, 2013 @ 12:15 am |
I think the points must be distributed in the whole intersection, since otherwise you are computing the eigenfunction on a non-planar domain in which the untested part of the intersection occurs twice, one for each side.
Comment by Lior Silberman — July 15, 2013 @ 12:26 am |
More detail: take two paper sectors, draw a disc on each (with the same radius) and glue them along the disc. You get a singular two-dimensional manifold. I think your intuition was that due to elliptic regularity the eigenfunction is real-analytic so it’s enough to study it on the disc, but the problem is that elliptic regularity only holds in neighbourhoods of regular points — the eigenfunctions of this space would be singular across the boundary of the disc (they’d be continuous, but I’ll be surprised if the derivatives were continuous).
Comment by Lior Silberman — July 15, 2013 @ 1:16 am
At the discrete level, if I’m choosing a finite number of points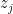 in the intersection domain, why should it matter whether they are confined to a smaller neighbourhood, or confined in the manner you suggested earlier? I can see that one configuration may give better conditioning than the other.
in the intersection domain, why should it matter whether they are confined to a smaller neighbourhood, or confined in the manner you suggested earlier? I can see that one configuration may give better conditioning than the other.
The equivalence statement – that truncated expansions are equal at these points, as are their gradients- should hold at all the points in the intersection, right? At least this is what I inferred from Section 3 in your current notes. If there’s something special about the choice of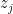 in Section 3, I don’t follow. I must be missing a key part of this algorithm.
in Section 3, I don’t follow. I must be missing a key part of this algorithm.
Comment by nilimanigam — July 15, 2013 @ 1:53 am
It would be the inner product of and
and 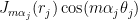 where
where 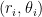 ,
, 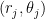 are the two different polar variables. It’s a good question whether one wants the L^2 or H^1 inner product. Currently, our theoretical guarantee of stability (i.e. that triples of Bessel expansions which nearly match at the overlapping regions are close to the true eigenfunction) requires matching in H^1 rather than just L^2. But maybe one can hope to also have numerical stability if one uses just L^2 instead of H^1. This would help out in the other part of the argument, when one takes a true eigenfunction for a perturbed triangle and extracts from it a triple of Bessel expansions in the reference triangle that nearly match, because it will be easier to use the bounds we have on the true eigenfunction (basically H^3 type regularity) to get L^2 bounds on the error here instead of H^1 error. (But we may be able to do both; even for H^1 we have two degrees of regularity to spare. Perhaps in the end it does not make much difference (morally, when one is close to an eigenfunction, H^1 norms should basically behave like
are the two different polar variables. It’s a good question whether one wants the L^2 or H^1 inner product. Currently, our theoretical guarantee of stability (i.e. that triples of Bessel expansions which nearly match at the overlapping regions are close to the true eigenfunction) requires matching in H^1 rather than just L^2. But maybe one can hope to also have numerical stability if one uses just L^2 instead of H^1. This would help out in the other part of the argument, when one takes a true eigenfunction for a perturbed triangle and extracts from it a triple of Bessel expansions in the reference triangle that nearly match, because it will be easier to use the bounds we have on the true eigenfunction (basically H^3 type regularity) to get L^2 bounds on the error here instead of H^1 error. (But we may be able to do both; even for H^1 we have two degrees of regularity to spare. Perhaps in the end it does not make much difference (morally, when one is close to an eigenfunction, H^1 norms should basically behave like  times the
times the 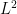 norm, so it may just end up being essentially a rescaling). We could try it both ways (and also with the sample points z_j) and see which way leads to better estimates for the eigenvalue and better stability properties (though this would require working out the truncation and distortion errors in several norms: L^2, H^1, and also sup norm).
norm, so it may just end up being essentially a rescaling). We could try it both ways (and also with the sample points z_j) and see which way leads to better estimates for the eigenvalue and better stability properties (though this would require working out the truncation and distortion errors in several norms: L^2, H^1, and also sup norm).
I see in Nilima’s notes that as an alternative to drawing sectors up to the orthocentre, one could instead use the incircle together with the sectors that reach up to the points of tangency of the incircle with the sides of the triangle. Then one would not be comparing sectors with each other, but instead comparing the three sectors to a Bessel expansion for the incircle. My guess is that this scheme would be roughly comparable in accuracy with the orthocentre scheme but would be slightly trickier to implement, so perhaps we can stick with the orthocentre scheme instead and not try to paste in the incircle as well. (Nice to see classical geometry come in here, though!)
Comment by Terence Tao — July 15, 2013 @ 12:31 am |
I also enjoyed doing classical geometry last night. I don’t usually get to do this for work :-)
Later tonight I’ll try updating the notes with an bound on truncation error of the derivative, which would give L^2 and H^1 bounds by integration.
bound on truncation error of the derivative, which would give L^2 and H^1 bounds by integration.
Do you have an intuition how much better direct bounds would be?
Comment by Lior Silberman — July 15, 2013 @ 2:11 am |
One of the basic advantages of L^2 based estimates over sup-norm estimates is that one gets to square-sum the different Bessel modes (due to orthogonality in the angular variable) rather than use the triangle inequality. Dually, one gets to have control on the coefficients
control on the coefficients  rather than sup norm control for a similar reason. The upshot of both of these improvements is that the k summation in your current bounds for the truncation error gets replaced with a supremum over k. If the k summation is slowly convergent (due to the slow decay of the geometric factor
rather than sup norm control for a similar reason. The upshot of both of these improvements is that the k summation in your current bounds for the truncation error gets replaced with a supremum over k. If the k summation is slowly convergent (due to the slow decay of the geometric factor  ) then this could make a noticeable difference. (There is also the fact that we get to use the L^2 mean of the cosine function rather than the sup norm, which saves an additional factor of
) then this could make a noticeable difference. (There is also the fact that we get to use the L^2 mean of the cosine function rather than the sup norm, which saves an additional factor of 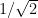 , but this is minor.) Finally the estimates will be in terms of the L^2 norm of u rather than the sup norm of u, which saves us a factor involving the Sobolev constant (which we have some bounds for but they are not optimal.)
, but this is minor.) Finally the estimates will be in terms of the L^2 norm of u rather than the sup norm of u, which saves us a factor involving the Sobolev constant (which we have some bounds for but they are not optimal.)
Comment by Terence Tao — July 15, 2013 @ 3:03 am |
Thanks! I updated the notes late last night. I have a side hope that is uniformly bounded away from one (
is uniformly bounded away from one (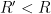 ,
, 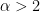 in acute triangles and the case where R’ approaches R is when the angle is small so
in acute triangles and the case where R’ approaches R is when the angle is small so  is big. In that case the two bounds will differ by constants (which could still be pretty large).
is big. In that case the two bounds will differ by constants (which could still be pretty large).
I’ll try adding L^2 and H^1 bounds.
Comment by Lior Silberman — July 15, 2013 @ 3:48 pm
Also to keep track, here’s a quick summary of the finite-element based computations I’ve done so far. I try to point out which steps I consider validated numerics.
1. Sampling in parameter space: how many triangles we need to check the conjecture on depends on the angles of the triangle. Terry provided estimates on how ‘close’ in parameter space triangles needed to be to control the sup norm to within specified tolerance (1e-8). These estimates depended on the spectral gap. I’ve used a sampling protocol which told me which triangles to check. Since the estimates depend on the spectral gap, which is only approximated, I consider this step solid but not ‘validated’.
2. Interval check of eigenpair: For each discrete system generated, eigenvalues and eigenfunctions are computed using the Lanczos method. The quality of these is checked for the given discrete matrix, using interval arithmetic. I consider this step validated.
3. Eigenvalue calculation: assuming discrete eigenvalues are exactly computed, the use of P1 conforming and P1 non-conforming finite elements gives approximations of eigenvalues from above and below. This is a theorem. For each triangle we examine, we have a ‘bracketing’ of the true eigenvalue. The width of the interval is wider than rounding errors. I consider this verification ‘validated’.
4. FEM accuracy: since P2 conforming approximations are guaranteed to converge fast to the true eigenvalue and eigenfunction (in exact arithmetic), eigenvalues and eigenfunctions are computed on a fine mesh (h=1e-5). These approximations are guaranteed to approach the true ones, and lie within the bracketing from step 3. They are also checked as per step 2. The eigenvalue approximations we obtain from this step, therefore, are good to 10 digits. In the L2 norm, the eigenfunctions are also close to the true ones. I consider this step validated.
But in the absence of an a posteriori estimate of the form I am not happy asserting that the computed eigenfunction is close in the sup norm to the true one. In the ‘eyeball’ norm, and certainly for the few cases one can check by hand, this seems true. But I don’t consider this assertion ‘validated’ yet.
I am not happy asserting that the computed eigenfunction is close in the sup norm to the true one. In the ‘eyeball’ norm, and certainly for the few cases one can check by hand, this seems true. But I don’t consider this assertion ‘validated’ yet.
5. Location of extrema: The eigenfunction computed in step 4. consists of piecewise quadratic functions on simplicial (triangular) subdomains of the triangle.
Method 1: Use an L2 projection of this eigenfunction onto a P1 conforming space on a much finer tesselation. The extrema will lie on nodes of the tesselation; locating the global max and min is easy. This step is simple. If the extrema of this projection lie on the vertex of the triangle, one can legitimately conclude the extrema lies in a small simplex containing that triangle. Terry’s calculations then force the extremum to be at the vertex.
Method 2: On each simplex, the location of the extrema of the quadratic can be written down in terms of the degrees of freedom using basic calculus. These formulae directly used aren’t numerically stable to round-off. With some irritating rewriting, they are stabler. Using these, one can again locate global max and min. This step is validated, but I lose digits.
I’ve checked 8000 acute triangles based on the sampling strategy of Step 1, and in all instances the extrema of the computed eigenfunctions lie on the vertices.
Comment by nilimanigam — July 14, 2013 @ 1:52 am |
It is great that the project is gaining speed again. The numerical approach looks really promising. It also gets very advanced for me. I am not sure how important gap estimates are, but they can be obtained analytically. Even better bounds can be obtained using a mixture of numerics at sampling points and analytic methods to extend these to other triangles (even around equilateral). This last approach is a somewhat brutal version of the simplicity argument.
I have cleaned up the simplicity argument and typed it with most of the details included. It relies on an algorithm for proving ugly polynomial inequalities that can be applied by hand, but is much easier to use with Mathematica (or any other computer language). Here is the argument, a somewhat messy mathematica file (and its pdf version). Mathematica file has all the applications of the algorithm visualized.
Click to access simple.pdf
http://math.uoregon.edu/~siudeja/simple.nb
Click to access simple.nb.pdf
Comment by siudej — July 14, 2013 @ 9:29 am |
Regarding Step 1 and positions of the extrema, I am 200% sure that the eigenfunction is monotonic on 2 longest sides and changes sign there. It also has one extremum and fixed sign on the shortest side. The only exception is right triangles, but there the eigenfunction is monotonic on all sides. Of course I have no proof whatsoever for acute triangles.
Comment by siudej — July 14, 2013 @ 9:43 am |
Thanks for the simplicity notes, I’m reading through them now. Nice work!
Your comment above is promising. So, if I understand correctly, one global extremum is guaranteed on the shortest side, and the nodal line cuts the longest sides, say at points P and Q. Is this correct?
Suppose the shortest side is BC.
The nodal line for the eigenfunction cuts the triangle into two pieces, APQA and BPQCB (there aren’t loops or multiple nodal lines that I observe. Maybe this is a theorem?)
Because of the signs, one must only establish that in the subdomain of the triangle APQA the non-zero extremum occurs at A. A is already extremizing along the edges. Maybe there are convexity arguments to force the non-zero extremum in APQA to A?
If this is a theorem, it is very helpful for the numerics, since it constrains where one looks for the extrema.
Comment by nilimanigam — July 14, 2013 @ 3:36 pm |
Nodal line cuts the triangle exactly as you describe, but I cannot even show that it cuts the longest side, let alone 2 longest. I do not even know how to prove that the absolute value of the extremum at A is larger than the one on the opposite side. Nor I can prove existence of the extremum on the short side. Sorry.
One thing that is known, is that nodal line has no loops, and it is just one curve. This curve is definitely convex, but this is also not known.
Comment by siudej — July 14, 2013 @ 4:03 pm |
This project is a mathematically rich one indeed!
Even if the hot spots conjecture is settled using one set of techniques, reading through this project one finds interesting questions in several areas. At least in numerical analysis there are some nice problems which have cropped up, and which it would be good to solve. The same is true of the conjecture you have above. If you are able to make progress on this conjecture, and are able to generalize it to other polygons, then this would have nice implications for shape optimization and boundary control problems.
Comment by nilimanigam — July 14, 2013 @ 4:13 pm |
A small observation:
If we construct an approximate eigenfunction (obeying the Neumann boundary conditions) and an approximate eigenvalue
(obeying the Neumann boundary conditions) and an approximate eigenvalue  whose residual
whose residual  is small, then we have obtained a rigorous bound for the nearest true eigenvalue
is small, then we have obtained a rigorous bound for the nearest true eigenvalue 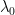 to
to  , thanks to the inequality
, thanks to the inequality
that is easily proven from eigenfunction expansion. In particular, if we have three Bessel series ,
,  in three sectors
in three sectors 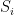 whose discrepancies
whose discrepancies  are small, then we can rigorously obtain an interval centred at
are small, then we can rigorously obtain an interval centred at  capturing a true eigenvalue by using smooth partitions of unity as discussed earlier (e.g. in Lior’s notes). If we have some way of getting a good rigorous lower bound on the third eigenvalue, then we may be able to say for certain that this interval is capturing the second eigenvalue.
capturing a true eigenvalue by using smooth partitions of unity as discussed earlier (e.g. in Lior’s notes). If we have some way of getting a good rigorous lower bound on the third eigenvalue, then we may be able to say for certain that this interval is capturing the second eigenvalue.
So if we use the H^1 norm on the overlapping regions to measure error (as can be done by precomputing H^1 inner products of Bessel basis functions, as discussed earlier), then we can rigorously confine the true eigenvalue of the reference triangle, which then also confines the true eigenvalue of nearly triangles as well by considering the behaviour of the Rayleigh quotient under affine transformations. This could be a good warmup project before we try to rigorously control the eigenfunctions as well as the eigenvalues.
Comment by Terence Tao — July 15, 2013 @ 2:45 am |
I can write up some code to numerically compute the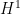 inner product on
inner product on 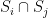 , but I suspect there’s a clever way to write this domain so that one can use symbolic computation instead.
, but I suspect there’s a clever way to write this domain so that one can use symbolic computation instead.
Your comment actually reminds me of something I should do, anyway, for the FEM calculations. Since I use piecewise quadratics, I can certainly compute for the approximate eigenpair
for the approximate eigenpair  .
.
Comment by nilimanigam — July 15, 2013 @ 3:00 am |
Do your piecewise quadratics obey the Neumann condition exactly or only approximately? If the latter, then we’ll have to work a bit harder to get a rigorous bound for the true eigenvalue (it’s still possible, but one has to get good H^2 bounds on a function with prescribed normal derivative that one has to subtract off from the piecewise quadratic function), though one could still pretend that the inequality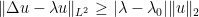 is still true for this test function to get a rough sense of what to expect. (For instance, if we can get the interval confining the eigenvalue small enough, Siudeja’s explicit inequalities for
is still true for this test function to get a rough sense of what to expect. (For instance, if we can get the interval confining the eigenvalue small enough, Siudeja’s explicit inequalities for  may be enough to prove that the interval we found actually contains
may be enough to prove that the interval we found actually contains 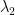 , as long as we are far enough away from the equilateral case of course.)
, as long as we are far enough away from the equilateral case of course.)
Comment by Terence Tao — July 15, 2013 @ 3:26 pm |
The FEM approximants satisfy the Neumann condition exactly.
Comment by nilimanigam — July 15, 2013 @ 3:45 pm |
Jie Shen, who has a lot of experience in using spectral methods (ie based on eigenfunction expansions of the kind we’re thinking of), has an interesting approach:
Click to access SWL_SINUM09.pdf
I hope he’ll contribute to this project!
Comment by nilimanigam — July 15, 2013 @ 5:25 am |
Mateusz Kwasnicki and Tadeusz Kulczycki pointed out to me that in http://plms.oxfordjournals.org/content/101/2/589 they (with coauthors) glue together (using partition of unity) half-line solutions for fractional Laplacian to get great two sided bounds for eigenvalues on interval (analytically). They also have some numerical results that are accurate to 9 digits for both sides. This is of course a very different setting, but there are even fewer methods available for fractional Laplacian. This seems similar to the new numerical ideas discussed now.
Comment by siudej — July 18, 2013 @ 10:21 am |
Nice! I guess this confirms that these results can get good numerical bounds, at least for the model problem of controlling the eigenvalue rigorously. Nine digit accuracy for the eigenvalue is particularly reassuring, since I suspect that our control on eigenfunctions will be linearly sensitive to the accuracy of our eigenvalue. (I should work out exactly what this sensitivity is – it requires understanding how Bessel functions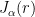 vary in the
vary in the  parameter, which is something which of course should be in the standard Bessel function literature, but I haven’t had the time to look carefully at it yet.)
parameter, which is something which of course should be in the standard Bessel function literature, but I haven’t had the time to look carefully at it yet.)
Comment by Terence Tao — July 18, 2013 @ 4:23 pm |
Good find! I don’t entirely understand the details of the numerical implementation yet, but the accuracy (and the intervals) are encouraging. Bartek, do you know how Mathematica locates eigenvalues of matrices?
As a side comment, this paper, as well as the idea of using local expansions patched together using partitions of unity, are reminiscent of the ‘shooting’method used in boundary value problems. They are also close somehow to the Schwarz iteration.
There are some nice identities involving the derivatives of Bessel functions in the order variable in the NIST website:
http://dlmf.nist.gov/10.38
Comment by nilimanigam — July 18, 2013 @ 5:01 pm |
I have found the following reference about methods used by Mathematica. This tutorial is obsolete, so they may have changed something. For small number of eigenvalues they use Arnoldi, otherwise LAPACK. There are some details in the tutorial.
http://reference.wolfram.com/mathematica/tutorial/LinearAlgebraMatrixComputations.html#1705931980
Comment by siudej — July 19, 2013 @ 7:38 am |
Here’s a non-technical ‘planning’ question. I’d like to understand what stage we’re at on this project. Is the current goal to
(a) find a way to compute the eigenfunction well?
(b) verify the quality of an eigenfunction, no matter how it is computed?
Would it be useful if I tried (b), ie, to verify the quality of the eigenfunctions I know how to compute (using the validated FEM strategy that’s up and running)? Terry’s ideas of using the local expansions to check eigenfunctions is certainly doable. But if this is inherently the wrong direction to proceed in, I don’t want to put time here.
Or would it be more sensible for me to switch to (a)? It would be a lot of fun for me personally to design, analyze and implement several algorithms for (a). But this would take me time, since there is a lot I’d need to learn and coding takes time. It is certainly better to let others with more expertise do this.
I’d like a sense of where I should be focussing.
Comment by nilimanigam — July 18, 2013 @ 5:01 pm |
I’ll add a third goal
(c) get good rigorous bounds on the second eigenvalue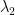 .
.
Progress on (b) can lead to progress on (c) in a number of ways: for instance if one has a putative eigenfunction that has mean zero and obeys the Neumann condition and is in H^1, then its Rayleigh quotient is an upper bound for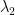 . If in addition it is in H^2, then its residual provides a rigorous interval for an eigenvalue to be contained in (and provided this interval lies below the best lower bound for
. If in addition it is in H^2, then its residual provides a rigorous interval for an eigenvalue to be contained in (and provided this interval lies below the best lower bound for  , this interval must be trapping
, this interval must be trapping 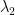 ). For these applications it does not matter at all where the approximate eigenfunction came from, so in particular FEM-generated eigenfunctions are OK.
). For these applications it does not matter at all where the approximate eigenfunction came from, so in particular FEM-generated eigenfunctions are OK.
The harder task is (a). As I see it we have basically two strategies here, both of which need (c) as a prerequisite (because the dependence on errors in the eigenvalue are likely to be linear in nature, or worse). One is to start with a high-quality putative eigenfunction (such as one generated from FEM methods, or from local Bessel expansions, or whatever else numerically seems to give good results), and try to rigorously show that it is close to the true eigenfunction (either of the same triangle, or a nearby triangle) in various norms (e.g. L^2, H^1, H^2, sup-norm, or Bessel coefficient comparison norms). Then one tries to show that the true eigenfunction obeys the hot spots conjecture. This route to (a) passes through (b), but one tricky thing here is that we will probably need H^2 control on the eigenfunctions in (b), H^1 will not be enough (because we don’t get a bound on the residual).
The second strategy is to try to control the Bessel coefficients of the true eigenfunction directly by using a least squares problem involving trying to get three truncated Bessel series to match. The true eigenfunction generates a competitor to this least squares problem (by truncating the three Bessel series) which should have a pretty small residual for the least squares problem; if the least squares problem is “well-conditioned” in some sense, this should place the Bessel coefficients of the true eigenfunction in a small ellipsoid, which hopefully is then enough to show that the true eigenfunction obeys the hot spots conjecture. Note that for this strategy one does not actually need an approximate eigenfunction to play with, although the minimiser of the least squares problem.
In any event, I think (c) is a good subgoal to aim for for now, as it is easier and is in any event going to be needed for the later goals. Maybe by the time we have achieved (c) we will have a clearer idea what to do for (a) or (b).
Comment by Terence Tao — July 18, 2013 @ 7:51 pm |
This goal (c) is eminently sensible, and very helpful to see stated as such. If I’m correct, at least one part of this analysis would involve the size of the products of basis functions.
here is some Matlab code for computing the L2 inner product of the (scaled) basis functions in the overlap domain. Change the quantities A(1), A(2) to vary the angles of the triangle. The expressions for the cartesian coordinates of the orthocenter, and the radii of the sectors, is in this file.
http://people.math.sfu.ca/~nigam/polymath-figures/hilbertprods.m
I’ve generated some examples in the notes here: http://people.math.sfu.ca/~nigam/polymath-figures/numbers1.pdf
let me know if there are other triangles for which this information would be useful.
Observation: as the integers n,m grow, the integral of the product on the overlap region of the sectors becomes small. This is not surprising, since these functions become oscillatory.
The H^1 code is still being debugged, and I’ll post it+ results when I get a chance.
Comment by nilimanigam — July 18, 2013 @ 10:59 pm |
Thanks for this!
I just realised though that to get smooth cutoff functions on the three sectors, they are going to have to stretch a little bit beyond the orthocentre, probably we should take them all the way to the altitude on the opposite side.
Actually, building the cutoff functions is going to be something of a pain – they have to be at least twice differentiable, and they also have to obey the Neumann condition, which is certainly doable but the formulae for the functions are going to be messy. One can take
is going to be something of a pain – they have to be at least twice differentiable, and they also have to obey the Neumann condition, which is certainly doable but the formulae for the functions are going to be messy. One can take  where each
where each 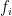 is supported on one of the sectors, positive on the interior of the sector, and is a twice differentiable function of the distance to the vertex; this will automatically obey the Neumann condition. I’m not sure exactly what the optimal choice of
is supported on one of the sectors, positive on the interior of the sector, and is a twice differentiable function of the distance to the vertex; this will automatically obey the Neumann condition. I’m not sure exactly what the optimal choice of 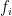 is though; one wants to keep
is though; one wants to keep  and
and 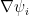 small in sup norm in order to control the residual
small in sup norm in order to control the residual 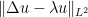 of the interpolated function
of the interpolated function 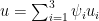 by the
by the 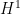 norm of the errors
norm of the errors  of the Bessel expansions
of the Bessel expansions  . (Alternatively, one could view
. (Alternatively, one could view  directly as a quadratic form of the Bessel coefficients of the
directly as a quadratic form of the Bessel coefficients of the 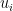 ; this would require one to compute inner products of
; this would require one to compute inner products of  with each other. Actually, this is probably the more efficient way to proceed numerically, although it does require us to decide exactly how to define the
with each other. Actually, this is probably the more efficient way to proceed numerically, although it does require us to decide exactly how to define the  .)
.)
Comment by Terence Tao — July 21, 2013 @ 5:59 am |
This reminds me of an older paper by Melenk and Babuska, in which they use partition of unity strategies to glue together FEM spaces. In section 3.3, they consider an example involving Fourier-Bessel functions.
Click to access eth-24741-01.pdf
I have to re-read this paper carefully. There may be good choices of partition of unity functions in Melenk’s thesis or in subsequent work.
There’s a nice paper by 1997 Toby Driscoll on essentially what Lior was suggesting. He has a cure for the problems I was encountering with the implementation.
Click to access 1997-Driscoll-1.pdf
Comment by nilimanigam — July 21, 2013 @ 4:13 pm |
Driscoll’s paper is very interesting. Collocation seems to be a bad idea, but optimizing a quadratic form seems to work, and he even has an idea to improve the precision of the minimum-finding.
Re-reading Booker et al I realized they also do something different. In out setting it amounts to the following: The Fourier–Bessel coefficient is given by integrating
is given by integrating  along any circular arc centered at the vertex. If you take the arc far out, then every point on the arc will be close to the other vertices — so you can evaluate the integral by using the other expansions. This now gives a linear system, exactly
along any circular arc centered at the vertex. If you take the arc far out, then every point on the arc will be close to the other vertices — so you can evaluate the integral by using the other expansions. This now gives a linear system, exactly  if you have
if you have  degree of freedom. Furthermore, simply updating each
degree of freedom. Furthermore, simply updating each  in order amounts to Gauss–Seidel iteration for solving this system. Also, since we are integrating a cosine along the arc, simply using equidistant points along the arc gives an exact integration scheme.
in order amounts to Gauss–Seidel iteration for solving this system. Also, since we are integrating a cosine along the arc, simply using equidistant points along the arc gives an exact integration scheme.
[was ill last week hence the silence]
Comment by Lior Silberman — July 21, 2013 @ 10:55 pm |
Lior, when you say using equidistant points on the arc, do you mean using the trapezoidal rule?
Comment by nilimanigam — July 23, 2013 @ 2:56 pm |
Here’s a suggestion for partition of unity functions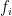 in Terry’s notation above. Here i denotes the ith vertex. Let
in Terry’s notation above. Here i denotes the ith vertex. Let  be the polar coordinates of a point, with this vertex as origin.
be the polar coordinates of a point, with this vertex as origin.
c is some positive constant.
Comment by nilimanigam — July 23, 2013 @ 3:00 pm |
Dear Nilima,
I’m assuming you want instead of
instead of  (using Lior’s notation) to maintain Neumann conditions. Actually it seems that one doesn’t need the cosine at all;
(using Lior’s notation) to maintain Neumann conditions. Actually it seems that one doesn’t need the cosine at all; 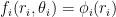 might be a better choice (not only because it is a simpler expression, but because first and second derivatives of the resulting functions
might be a better choice (not only because it is a simpler expression, but because first and second derivatives of the resulting functions  look smaller, which is what we really are after).
look smaller, which is what we really are after).
In the same vein, since we only need second derivative control on the cutoffs, a cutoff might be more expensive than what we really need; one might be able to get away with just the quadratic cutoff
cutoff might be more expensive than what we really need; one might be able to get away with just the quadratic cutoff  , for instance.
, for instance.
Comment by Terence Tao — July 23, 2013 @ 9:59 pm |
Dear Terry, . Sorry about the error.
. Sorry about the error.
Yes, you are correct about the extra factor of
I was indeed trying to ensure the Neumann condition on the edges. I was unsure if, for the analysis, non-zero angular derivatives of the partition functions are needed.
Comment by nilimanigam — July 23, 2013 @ 10:24 pm |
I’d go with functions of the radius only. This helps with the derivative bounds since the angula derivative vanishes. Some thoughts:
1. It would be nice for the function to die before we reach the other edge, so as to minimize the intersection between the parts of the partition. avoids a potential singularity at
avoids a potential singularity at  , but perhaps this isn’t an issue.
, but perhaps this isn’t an issue.^2](https://s0.wp.com/latex.php?latex=%5Cleft%5B1-c%28r-R_1%29%5E2%5Cright%5D%28R_2-r%29%5E2&bg=ffffff&fg=000000&s=0&c=20201002) in
in ![[R_1,R_2]](https://s0.wp.com/latex.php?latex=%5BR_1%2CR_2%5D&bg=ffffff&fg=000000&s=0&c=20201002) . This also avoid the possible singularity at the vertex. We can later optimize the two radii.
. This also avoid the possible singularity at the vertex. We can later optimize the two radii.
2. Naively, using a function of
3. It may be nice to have the function constant for a good part of the sector, so perhaps something like
Comment by Lior Silberman — July 24, 2013 @ 5:04 am |
Actually, because the sectors don’t reach the other vertices, the functions will automatically be constant near their associated vertex regardless of what the
will automatically be constant near their associated vertex regardless of what the 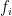 are doing. So 2. and 3. are indeed not an issue. Regarding 1, there is a tradeoff: if one narrows the sectors, then there is a smaller region of interaction between the
are doing. So 2. and 3. are indeed not an issue. Regarding 1, there is a tradeoff: if one narrows the sectors, then there is a smaller region of interaction between the  , but then the first and second derivatives of
, but then the first and second derivatives of  get larger. I’m not sure at present what the right balance is.
get larger. I’m not sure at present what the right balance is.
Comment by Terence Tao — July 24, 2013 @ 5:13 am |
Playing around with some partition-of-unity functions mentioned above, it appears the angles of the triangle will play an important role in how large (in L^2)$ the gradients of these functions are in the regions where they are not constant. This is obvious in hindsight- the functions have to decay to zero, and the region in which they do so depends on the opening angle of the sector.
I’ll post some figures in the morning.
Comment by nilimanigam — July 24, 2013 @ 5:23 am |
Bartlomiej Siudeja just drew my attention to two recent papers of Miyamoto, http://jmp.aip.org/resource/1/jmapaq/v50/i10/p103530_s1?isAuthorized=no and http://link.springer.com/article/10.1007/s13160-012-0091-z , that among other things establish the hot spots conjecture for nearly round domains and for isosceles subequilateral triangles, using a robust analytic method which looks attractive for attacking other triangles (I understand Bartlomiej is in the process of writing up some notes or a paper exploring this). Looks like something to discuss for our project (maybe I’ll start a new blog post for this once I digest the papers).
Comment by Terence Tao — August 3, 2013 @ 1:28 am |
Yes, Bartek pointed out this work (we met at a conference this week). It looks promising, but I do not understand the details.
Comment by nilimanigam — August 3, 2013 @ 2:27 am |
Miyamoto’s method is very simple, clever and gives great results. His nearly round domain paper relies on existence of a function satisfying
satisfying on the boundary of the domain, [Edited by Bartek]
on the boundary of the domain, [Edited by Bartek]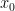 in the domain (e.g. radial Bessel with center at
in the domain (e.g. radial Bessel with center at 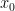 ).
).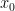 . If one can choose any point, then hot-spots conjecture holds. Unfortunately for triangles radial Bessel function (used in Miyamoto’s paper) is not good enough to cover corners. But one can eliminate critical points that are closer than about 85%-95% of the diameter to all vertices (depending on a triangle) .
. If one can choose any point, then hot-spots conjecture holds. Unfortunately for triangles radial Bessel function (used in Miyamoto’s paper) is not good enough to cover corners. But one can eliminate critical points that are closer than about 85%-95% of the diameter to all vertices (depending on a triangle) .
1) eigenvalue equation (no boundary condition) with exactly the same eigenvalue as the given domain, e.g. cosine or Bessel with appropriate scaling,
2)
3) critical point at the chosen point
If such function exists, then the second Neumann eigenfunction has no critical point at the chosen point
The second paper deals with critical points on the boundary of an isosceles triangle. His results cannot be directly applied to arbitrary triangles, but I have an almost ready pre-preprint with a refinement that can be applied to some triangles. I will post it in a day or two when it is more readable.
Comment by siudej — August 4, 2013 @ 4:20 am |
I started reading Miyamoto’s first paper at http://www.kurims.kyoto-u.ac.jp/preprint/file/RIMS1591.pdf . It is indeed a very clever criterion he has to rule out critical points at many interior points in a convex domain, though I was not able to verify it using your condition (2) above (instead I had the condition that had a definite sign on the boundary, either always positive or always negative).
had a definite sign on the boundary, either always positive or always negative).
The argument seems to go like this. Suppose for contradiction that the second eigenfunction has a critical point at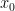 . Then by taking a linear combination of this function with
. Then by taking a linear combination of this function with  , one can obtain another solution
, one can obtain another solution  to the eigenfunction equation
to the eigenfunction equation  at the second eigenvalue which has a degenerate zero at
at the second eigenvalue which has a degenerate zero at 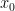 (
(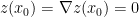 ) and which has negative normal derivative everywhere on the boundary. The degenerate zero means that the zero locus of z crosses itself at
) and which has negative normal derivative everywhere on the boundary. The degenerate zero means that the zero locus of z crosses itself at 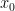 (excluding some very degenerate cases, such as when z vanishes completely), and one can show that this divides the domain into at least four regions, with z positive on at least two of them. On the regions where z is positive, integration by parts shows that the Rayleigh quotient is less than
(excluding some very degenerate cases, such as when z vanishes completely), and one can show that this divides the domain into at least four regions, with z positive on at least two of them. On the regions where z is positive, integration by parts shows that the Rayleigh quotient is less than  , and then by taking a linear combination of these two regions one can obtain a mean zero function with Rayleigh quotient less than
, and then by taking a linear combination of these two regions one can obtain a mean zero function with Rayleigh quotient less than  , a contradiction.
, a contradiction.
As you say, this rules out critical points occurring everywhere except on the edges and very close to each vertex; this looks like it will help with the numerical side of things. Also it seems that the flexibility to choose could be exploited beyond just picking the radial solution; there is a chance for some numerically verified strategy here to find other solutions to the eigenfunction equation which are decreasing on some deformed disk rather than a disk, which one might have a better chance of fitting the triangle inside.
could be exploited beyond just picking the radial solution; there is a chance for some numerically verified strategy here to find other solutions to the eigenfunction equation which are decreasing on some deformed disk rather than a disk, which one might have a better chance of fitting the triangle inside.
Comment by Terence Tao — August 5, 2013 @ 12:13 pm |
You are 100% right. I definitely oversimplified (2). Sorry. This is what you need on subdomains you describe. There is a slight chance that we could control where these domains touch the boundary. Then would not need to have the same sign on the whole boundary. Then (2) is exactly what one needs on subdomains.
would not need to have the same sign on the whole boundary. Then (2) is exactly what one needs on subdomains.
The argument relies on the ratio of the smallest eigenvalue on the disk and the radial mode eigenvalue of the same disk being less than 1/4. Then the radial mode rescaled to have the same eigenvalue covers the whole nearly round domain, regardless where the center is. For the unit square this ratio is 4 and for equailateral triangle just 3. Hence these radial eigenfunctions are as good for covering. There are however ellipses that may be better, but not so easy to handle. One needs to know that outer normal is negative/positive on the boundary and this is guaranteed for radially decreasing functions. Any function with angular dependence will not be so easy.
Comment by siudej — August 5, 2013 @ 3:17 pm |
It would certainly be excellent (from the point of view of validated numerics) to be able to shrink the candidate search region for extrema as you describe, with computable quantities specifying where the search should focus.
If ellipses can be used instead, then presumably a local change to elliptical coordinates, followed by the use of Mathieu functions, will be useful.
For reference, here’s a nice article by Steve Zelditch in which he discusses the form (and properties) of eigenfunctions in some specific instances. http://www.ms.uky.edu/~perry/CBMS/EigenfsJune9.pdf
Also for reference (and possible future use) is this paper by Kuttler in which he summarized numerical approaches for some standard domains. http://epubs.siam.org/doi/abs/10.1137/1026033
Comment by nilimanigam — August 5, 2013 @ 3:34 pm |
I agree that if one uses a non-radial test function then the condition on the normal derivative becomes messy to verify, but I think for a validated numeric approach it is still feasible to work out when the condition applies. One could imagine a brute force approach where one explores Miyamoto’s criterion for test solutions of the eigenfunction equation that consist of the zeroth and first angular modes (so something like a linear combination of
of the eigenfunction equation that consist of the zeroth and first angular modes (so something like a linear combination of 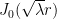 and
and  in polar coordinates around
in polar coordinates around 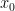 ). [EDIT: we need to work with
). [EDIT: we need to work with 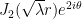 instead to keep it a critical point at
instead to keep it a critical point at 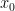 .] If one is lucky one might be able to cover the entire interior of the triangle just with these trial functions.
.] If one is lucky one might be able to cover the entire interior of the triangle just with these trial functions.
Incidentally, I was reading a 2004 paper of Filonov http://www.ams.org/journals/spmj/2005-16-02/S1061-0022-05-00857-5/S1061-0022-05-00857-5.pdf where he gives a short proof of Polya’s inequality that the second Neumann eigenvalue is dominated by the first Dirichlet eigenvalue in a Euclidean domain (actually he also proves the generalisation to higher eigenvalues by Friedlander) – this fact is used in Miyamoto’s argument to rule out loops in the zero set of z. It turns out that Filonov also uses an auxiliary solution to the eigenfunction equation, in this case the plane waves for some
for some  of magnitude
of magnitude  . Indeed, if
. Indeed, if  is a Dirichlet eigenfunction of eigenvalue
is a Dirichlet eigenfunction of eigenvalue  , a short computation shows that any linear combination of
, a short computation shows that any linear combination of  and
and 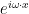 has Raleigh quotient equal to
has Raleigh quotient equal to  ; in particular one can take a linear combination of mean zero and conclude that
; in particular one can take a linear combination of mean zero and conclude that  is a lower bound for the Neumann eigenvalue (and with a bit more effort on can show that this is a strict inequality in two and higher dimensions, e.g. by varying
is a lower bound for the Neumann eigenvalue (and with a bit more effort on can show that this is a strict inequality in two and higher dimensions, e.g. by varying  ). It may be that a similar trick (i.e. working with
). It may be that a similar trick (i.e. working with 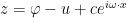 instead of
instead of  ) could boost the power of Miyamoto’s method (e.g. if we are somehow able to know on which sides of the triangle w-u is positive), but I haven’t played seriously with this yet.
) could boost the power of Miyamoto’s method (e.g. if we are somehow able to know on which sides of the triangle w-u is positive), but I haven’t played seriously with this yet.
Comment by Terence Tao — August 6, 2013 @ 8:32 am |
I have edited (2). With just the normal derivative the condition is ok.
Comment by siudej — August 5, 2013 @ 3:32 pm |
Bartek, I’m trying to understand from Miyamoto’s paper if his argument on the isoceles triangle could be extended to a generic constant-coefficient elliptic operator. I don’t see an immediate obstacle, but is there?
In other words, suppose one could somehow construct a target eigenfunction (like his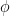 ) for the eigenvalue problem
) for the eigenvalue problem  . Can one use a variant of his argument for the eigenvalue problem with this new operator, with boundary conditions
. Can one use a variant of his argument for the eigenvalue problem with this new operator, with boundary conditions  ?
?
I ask because then one could map acute triangles to the reference triangle, and perhaps make the argument there on the perturbed Laplacian? His argument settles the conjecture on domains like the reference triangle.
Comment by nilimanigam — August 6, 2013 @ 3:15 pm |
I am not sure, I will have to think about this. There are certain conditions that must be satisfied first. E.g. eigenvalue bound that guarantees that cosine eigenfunction covers the whole triangle (cosine decreases on the whole triangle giving negative outer normal derivative). Also, cosine would not be the eigenfunction for other elliptic operators, and monotonicity (negative normal derivative condition) would not be immediate.
But this sounds like a possible approach.
Comment by siudej — August 8, 2013 @ 12:05 am |
X. Liu and S. Oishi just published a paper in SIAM J. Numer. Anal., in which they provide explicitly computable lower bounds for Dirichlet and Neumann eigenvalues on polygonal domains (using finite elements). They suggest a validated approach which is very close to the one we’ve been discussing here.
Theirs is a clever strategy, relying on the Aubin-Nitsche trick. The idea is to use only conforming elements and an explicitly computable quantity. Note that the paper does not provide the a posterior sup norm estimates one may need using a FEM approach. However, it *does* provide an explicit way to get lower bounds on the eigenvalues.
Click to access 120878446.pdf
I’m going to give their strategy a try this week.
Comment by nilimanigam — August 3, 2013 @ 4:15 am |
Here is my preprint with a partial resolution of the conjecture and the reduction to the boundary problem.
Click to access hotspots.pdf
There is certainly some room for improvement. In particular when the eigenvalue bound in Lemma 1.6 does not hold, one might try to use a more complicated eigenfunction instead of cosine. I have done some Mathematica/numerical experiments and for equilateral triangle one might take a rectangle eigenfunction and eliminate critical points on the middle 70% of each side. I wasn’t able to find any eigenfunction, that would give good results for critical points near vertices.
Also, if Lemma 1.6 could be somehow applied to all sides, then the positive minimum (negative maximum) case can happen only once, since nodal line cannot start and end on the same side. This would mean no critical points on two sides, hence hot-spots conjecture would hold.
Comment by siudej — August 8, 2013 @ 12:17 am |
Bartek, this is very nice work! I have not checked all the details but it looks promising indeed. It seems that you’ve got a very nice proof (Theorem 1.4) for the triangles which have one angle small (less than pi/6)…. and these are usually cases in which naive mesh refinements of FEM don’t do so well. Good work!
Comment by nilimanigam — August 8, 2013 @ 10:41 pm |
Very nice indeed! I will try to write a new blog post for this polymath project with a brief summary of some of the new ideas here (this thread is getting too long to follow easily). The reduction to eliminating critical points on edges rather than the interior looks particularly promising, and it is great that the narrow triangles have been eliminated as they were looking a bit difficult to treat from the numerical perspective.
I have some ideas about how to push further the analysis of the nodal domains of a derivative of u (used in your proof of Theorem 1.3). Firstly it seems that if one uses the Neumann boundary condition of u and some integration by parts, one can compute rather exactly the functional
of u (used in your proof of Theorem 1.3). Firstly it seems that if one uses the Neumann boundary condition of u and some integration by parts, one can compute rather exactly the functional ![{\mathcal H}[ u_x 1_F ]](https://s0.wp.com/latex.php?latex=%7B%5Cmathcal+H%7D%5B+u_x+1_F+%5D&bg=ffffff&fg=000000&s=0&c=20201002) of various nodal components of this derivative. Also there appear to be quite a few nodal domains: if one takes an edge where u changes sign, and assumes that there is at least one critical point in that edge, it seems to me that there must in fact be two critical points on that edge (because u has a local maximum at one end of the edge and a local minimum at the other). I haven’t fleshed out the details of this yet though.
of various nodal components of this derivative. Also there appear to be quite a few nodal domains: if one takes an edge where u changes sign, and assumes that there is at least one critical point in that edge, it seems to me that there must in fact be two critical points on that edge (because u has a local maximum at one end of the edge and a local minimum at the other). I haven’t fleshed out the details of this yet though.
Comment by Terence Tao — August 9, 2013 @ 8:25 am |
A quick update on the strategy suggested in: http://www.xfliu.org/homepage/pdf/120878446.pdf
The analysis there allows us to use piecewise conforming P1 elements, and obtain _computable_ constants, such that one can obtain the a posteriori bounds
such that one can obtain the a posteriori bounds 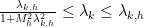 . Here the computed eigenvalue
. Here the computed eigenvalue 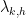 is an approximation of the kth true eigenvalue on a polygonal domain.
is an approximation of the kth true eigenvalue on a polygonal domain.
I’m re-doing the computations of the first two eigenvalues using this strategy, to get verified and validated bounds on the spectral gap in various parts of angle parameter space. Thanks to Bartek’s argument, I think the region of parameter space to explore is nicely reduced.
Comment by nilimanigam — August 9, 2013 @ 2:35 pm |
[…] the Polymath7 project to solve the hot spots conjecture for acute-angled triangles, superceding the previous thread; this project had experienced a period of low activity for many months, but has recently picked up […]
Pingback by Polymath7 research thread 5: the hot spots conjecture | The polymath blog — August 9, 2013 @ 7:22 pm |
I just started a new thread to help organise all the new discussion without being cluttered by the older comments.
Comment by Terence Tao — August 9, 2013 @ 7:23 pm |