There has been enough interest that I think we can formally declare Rota’s Basis Conjecture to be Polymath 12. I am told that it is standard Polymath practice to start a new blog post whenever the number of comments reaches about 100, and we have reached that point, so that is one reason I am writing a second post at this time. I am also told that sometimes, separate “discussion” and “research” threads are created; I’m not seeing an immediate need for such a separation yet, and so I am not going to state a rule that comments of one type belong under the original post whereas comments of some other type belong under this new post. I will just say that if you are in doubt, I recommend posting new comments under this post rather than the old one, but if common sense clearly says that your comment belongs under the old post then you should use common sense.
The other reason to create a new post is to take stock of where we are and perhaps suggest some ways to go forward. Let me emphasize that the list below is not comprehensive, but is meant only to summarize the comments so far and to throw in a few ideas of my own. Assuming this project continues to gather steam, the plan is to populate the associated Polymath Wiki page with a more comprehensive list of references and statements of partial results. If you have an idea that does not seem to fit into any of the categories below, please consider that to be an invitation to leave a comment about your idea, not an indication that it is not of interest!
Matroids with No Small Circuits
I want to start with an idea that I mentioned in my MathOverflow post but not in my previous Polymath Blog post. I think it is very promising, and I don’t think many people have looked at it. Geelen and Humphries proved that Rota’s Basis Conjecture is true for paving matroids. In the case of vector spaces, what this means is that they proved the conjecture in the case where every (n – 1)-element subset of the given set of n2 vectors is linearly independent. It is natural to ask if n – 1 can be reduced to n – 2. I have not digested the Geelen–Humphries paper so I do not know how easy or hard this might be, but it certainly could not hurt to have more people study this paper and make an attempt to extend its results. If an oracle were to tell me that Rota’s Basis Conjecture has a 10-page proof and were to ask me what I thought the method was, then at this point in time I would guess that the proof proceeds by induction on the size of the smallest circuit. Even if I am totally wrong, I think we will definitely learn something by understanding exactly why this approach cannot be extended.
Independent Partial Transversals
Let me now review the progress on the three ideas I mentioned in my first blog post. In Idea 1, I asked if the n2 vectors could be partitioned into at most 2n – 2 independent partial transversals. A nice proof that the answer is yes was given by domotorp. Eli Berger then made a comment that suggested that the topological methods of Aharoni and Berger could push this bound lower, but there was either an error in his suggestion or we misunderstood it. It would be good to get this point clarified. I should also mention that Aharoni mentioned to me offline that he unfortunately could not participate actively in Polymath but that he did have an answer to my question about their topological methods, which is that the topological concepts they were using were intrinsically not strong enough to bring the bound down to n + 1, let alone n. It might nevertheless be valuable to understand exactly how far we can go by thinking about independent partial transversals. Ron Aharoni and Jonathan Farley both had interesting ideas along these lines; rather than reproduce them here, let me just say that you can find Aharoni’s comment (under the previous blog post) by searching for “Vizing” and Farley’s comment by searching for “Mirsky.”
Local Obstructions
Idea 2 was to look for additional obstructions to natural strengthenings of Rota’s Basis Conjecture, by computationally searching for counterexamples that arise if the number of columns is smaller than the number of rows. Luke Pebody started such a search but reported a bug. I still believe that this computational search is worth doing, because I suspect that any proof that Rota’s Basis Conjecture holds for all matroids is going to have to come to grips with these counterexamples.
Note that if we are interested just in vector spaces, we could do some Gröbner basis calculations. I am not sure that this would be any less computationally intensive than exhausting over all small matroids, but it might reveal additional structure that is peculiar to the vector space case.
Algebraic Geometry
There has been minimal progress in this (admittedly vague) direction. I will quote Ellenberg’s initial thoughts: “If you were going to degenerate, what you would need to do is say: is there any version of this question that makes sense when the basic object is, instead of a basis of an n-dimensional vector space V, a 0-dimensional subscheme of V of degree n which is not contained in any hyperplane? For instance, in 2-space you could have something which was totally supported at the point (0,1) but which was “fat” in the horizontal direction of degree 2. This is the scheme S such that what it means for a curve C to contain S is that S passes through (0,1) and has a horizontal tangent there.”
Let me also mention that Jan Draisma sent me email recently with the following remarks: “A possible idea would be to consider a counterexample as lying in some suitable equivariant Hilbert scheme in which being a counterexample is a closed condition, then degenerate to a counterexample stable under a Borel subgroup of GLn, and come to a contradiction. ‘Equivariant’ should reflect the action of GLn × (Sn ⋉ Snn). However, I have not managed to make this work myself, even in low dimensions. In fact, having a good algebro-geometric argument for the n = 3 case, rather than a case-by-case analysis, would already be very nice!”
Alon–Tarsi Conjecture
Now let me move on to other ideas suggested in the comments. There were several thoughts about the Alon–Tarsi Conjecture that the Alon–Tarsi constant Lneven – Lnodd ≠ 0 when n is even. Rebecca Stones gave a formula that, as Gil Kalai observed, equated the Alon–Tarsi constant with the top Fourier–Walsh coefficient for the function detn; i.e., up to sign, the Alon–Tarsi constant is
ΣA (–1)σ(A) det(A)n,
where the sum is over all zero-one matrices and σ(A) is the number of zero entries in A. This formula suggests various possibilities. For example one could try to prove that Lneven – Lnodd ≢ 0 (mod p) where p = 2n + 1 is prime, because in this case, det(A)n must be 0, 1, or –1. This would already be a new result for n = 26, and the case n = 6 is small enough to compute explicitly and look for inspiration. Luke Pebody posted the results of some computations in this case.
Another possibility, suggested by Gil Kalai, is to consider a Gaussian analogue. Instead of random zero-one matrices, consider random Gaussian matrices and try to understand the Hermite expansion of detn, in particular showing that the coefficient corresponding to all ones is nonzero. This might be easier and might give some insight.
Note also that in the comments to my MathOverflow post, Abdelmalek Abdesselam proposed an analogue of the Alon–Tarsi conjecture for odd n. I do not think that many people have looked at this.
Generalizations and Special Cases
Some generalizations and special cases of the conjecture were mentioned in the comments. Proving the conjecture for graphic matroids or binary matroids would be an enormous advance. There is a generalization due to Jeff Kahn, in which we have n2 bases Bij and we have to pick vij ∈ Bij to form an n × n grid whose rows and columns are all bases. Another generalization was prompted by a remark by David Eppstein: Suppose we are given n bases B1, …, Bn of a vector space of dimension m ≤ n, and suppose we are given an n × n zero-one matrix with exactly m 1’s in every row and column. Can we replace each 1 in the matrix with a vector in such a way that the m vectors in row i are the elements of Bi and such that the m vectors in every column form a basis?
Juan Sebastian Lozano suggested the following reformulation: Does there exist a group G such that V is a representation of G and there exists gi ∈ G such that gi Bi = Bi+1, and for every vector b ∈ B1,
span{g0b, …, gn – 1b} = V
where gi = gi … g1 and g0 is the identity?
Other Ideas
Fedor Petrov mentioned a theorem by him and Roman Karasev that looks potentially relevant (or at least the method of proof might be useful). Let p be an odd prime, and let V be the Fp-vector space of dimension k. Denote V* = V \ {0} and put m = |V*|/2 = (pk – 1)/2. Suppose we are given m linear bases of the vector space V
(v11, …, v1k), (v21, …, v2k), …, (vm1, …, vmk).
Then there exist pairwise distinct x1, …, xm, y1, …, ym ∈ V* and a map g:[m] → [k] such that for every i ∈ {1, …, m} we have yi – xi = vig(i).
Gil Kalai notes that the Alon–Tarsi conjecture is related to the coloring polynomial of a graph and asks if we can learn anything by considering more general polynomials such as
Π {(xi – λexj) : i < j, {i,j} = e ∈ E(G)},
where the λe are weights associated to the edges e.
Thank you for this wonderful summary!
Here are some very preliminary thoughts which might be of interest. I was thinking that a perhaps instructive structure might be the exterior algebra on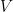 . There are three things that are attractive about this:
. There are three things that are attractive about this:
1) If we consider Rota’s basis conjecture to be a statement on the existence of certain non-zero elements in the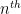 power of the graded algebra, then prima facie, it looks like the idea of a paving matroid is exactly a vector space upon which you can induct on the dimension of
power of the graded algebra, then prima facie, it looks like the idea of a paving matroid is exactly a vector space upon which you can induct on the dimension of 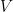 when proving the existence of these non-zero elements. I don’t think that this will give new information about the matroid problem — in fact it seems to me that the obstruction to doing this more generally is exactly the combinatorial/independence problem which the more general matroid approach aims to solve. However, if there is some structure specific to the vector space case, as opposed to the matroid, it seems the exterior algebra would be the natural place to capture it.
when proving the existence of these non-zero elements. I don’t think that this will give new information about the matroid problem — in fact it seems to me that the obstruction to doing this more generally is exactly the combinatorial/independence problem which the more general matroid approach aims to solve. However, if there is some structure specific to the vector space case, as opposed to the matroid, it seems the exterior algebra would be the natural place to capture it.
2) I do not understand fully the discussion of the Alon–Tarsi Conjecture above, but it seems that if we are talking about the signs of permutations (i.e. looking for odd v even latin squares, where the elements in our squares are basis elements), then one might be able to recover the formula given by Rebecca Stone by considering the action of on the highest exterior power in the exterior algebra. This might lend itself to some generalization (it seems to me that this is roughly the context of the mathoverflow question you link on the Alon–Tarsi Conjecture for odd
on the highest exterior power in the exterior algebra. This might lend itself to some generalization (it seems to me that this is roughly the context of the mathoverflow question you link on the Alon–Tarsi Conjecture for odd  , not with the exterior algebra, but with the tensor algebra, but that was just at a glance).
, not with the exterior algebra, but with the tensor algebra, but that was just at a glance).
3) Speaking of my reformulation on the last post: one can probably make a representation theoretic reformulation on the exterior algebra (e.g. maybe using the ‘induced representation’, meaning the representation passed into the exterior algebra) in which one might get explicit conditions on the determinants of the things in the image of the homomorphism into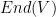 .
.
Anyway, my general point is simply that the exterior algebra might be a good place to think about the intersection of some of the approaches, which might help in the solving the problem, even if I doubt it is anywhere near enough on its own.
Comment by Juan Sebastian Lozano — March 7, 2017 @ 12:24 am |
Small comment on the algebraic geometry, still with very little content: Draisma’s comment is a much better way of saying what I was trying to say. Or rather, you might say: the content of my question is to ask what it would *mean* for a degenerate (e.g. Borel-fixed) object to be a “counterexample” to Rota (since it wouldn’t literally be subject to Rota’s conjecture in its original form.) I also want to endorse Draisma’s bringing up of the symmetry group GL_n × (S_n ⋉ S_n)^n, which acts on every vector space in this whole story and their symmetric powers too. What do we know about the ring of invariants?
Comment by JSE — March 7, 2017 @ 5:04 am |
I briefly discussed Draisma’s idea with Patrick Brosnan. One somewhat annoying fact is that Rota’s Basis Conjecture (or any variation or generalization that I have seen) hypothesizes that certain sets are bases, and being a basis is an open condition rather than a closed condition. I’m not sure how serious an obstacle this is?
Comment by tchow8 — March 28, 2017 @ 3:00 pm |
Have people seen this paper that just came out? It should be checked.
Carlos Gamas, ON THE CONJECTURE OF ALON-TARSI, Gulf Journal of Mathematics Vol 4, Issue 4 (2016) 108-116
Abstract. The Alon-Tarsi Conjecture states that for even n, the number of even latin squares of order n differs from the number of odd latin squares. In this note we prove that this conjecture is true if and only if there exists a permutation ζ ∈ S_{n^2} and a spherical function, φ, such that φ(ζ)\ne 0.
Comment: it looks like there are a couple of misprints in this paper. Hopefully they are not serious. (Both the spherical function and the permutation are defined at the beginning of the paper. So the actual statement in the abstract could be misleading?)
Comment by David Glynn — March 7, 2017 @ 9:33 am |
It seems that the Gaussian analog is actually equivalent to the Alon-Tarsi conjecture.
It can be formulated as follows:
Let be even and let
be even and let  be a random
be a random 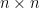 matrix. Then the expectation
matrix. Then the expectation
(Perhaps it is positive.)
We can take to be a random Boolean matrix with
to be a random Boolean matrix with 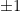 entries or a random Gaussian matrix with entries distributed
entries or a random Gaussian matrix with entries distributed  .
.
There is maybe some hope that because we know a lot about random Gaussian matrices (and correlation inequalities for Gaussian measures) there will be some other way/formula showing that the expectation in question for the Gaussian case is positive.
Comment by Gil Kalai — March 7, 2017 @ 2:00 pm |
Sorry to be dense, but why is the Gaussian analog equivalent to the Alon-Tarsi conjecture?
Comment by tchow8 — March 10, 2017 @ 12:09 am |
Suppose the elements of X are independent, symmetric about 0 and each have non-0 finite variance. We do not assume identical distributions.
Express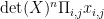 as a polynomial in the
as a polynomial in the  .
.
It is a homogeneous polynomial of degree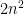 in
in 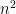 variables, in which each monomial contains each variable at least once.
variables, in which each monomial contains each variable at least once.
The expected value of any monomial is 0 if it has a variable raised to an odd power (since each variable is symmetric around 0 and they are all independent). Any monomial that is not of such a form must include every variable at least twice. By the degree condition, it must include each variable exactly twice.
Therefore the expectation of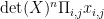 is equal to
is equal to 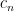 times the product of the variances of the cells, where
times the product of the variances of the cells, where 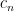 is independent of the distribution of the cells, and is equal to the
is independent of the distribution of the cells, and is equal to the  coefficient in
coefficient in  .
.
Finally: can be written as the sum of elements
can be written as the sum of elements  of the product of the signs of the sigmas times
of the product of the signs of the sigmas times  , which is equal to
, which is equal to  precisely when the sigmas form the rows of a Latin square.
precisely when the sigmas form the rows of a Latin square.
Therefore Alon-Tarsi is equivalent to the expectation of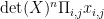 being non-0.
being non-0.
Comment by Luke Pebody — March 28, 2017 @ 6:38 pm |
So, for n=2, I looked for a simple expression for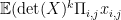 and proved that for even k it is -((k+2)*k*k!)/8.
and proved that for even k it is -((k+2)*k*k!)/8.
I then generated the same numbers for n=4, but haven’t been able to see what the formula could be:
The sequence goes:
576 for k = 4
14929920 for k = 6
534252257280 for k = 8
29855671566336000 for k = 10
2594739381460402176000 for k = 12
341103472674836305674240000 for k = 14
The quotients of consecutive terms are:
25920/1, 35784/1, 3967700/71, 313482312/3607, 444727920/3383
In the spirit of throwing pasta at the wall and seeing what sticks, I thought I would share these numbers here.
Comment by Luke Pebody — March 30, 2017 @ 6:25 am |
Tim asked me to write something about online versions of Rota’s Basis
conjecture. Here, the n bases arrive one at a time, and after you receive
the i-th basis, you have to decide immediately in what order to write it
as i-th row of the array you are creating. Of course, the goal is that
the columns of the eventual array are again independent. Is
there an algorithm that does this for i up to and including n? There
are at least two versions of this question:
(1) The input consists of vectors in a vector space. In this case,
for _even_ n, the online version still follows from Alon-Tarsi (in
char 0), and for _odd_ n any online algorithm can be fooled in the
last steps (if the field contains sufficiently many roots of unity);
see https://arxiv.org/pdf/1312.5953.pdf
(2) The input consists of elements in an abstract matroid. In other
words, when the new basis arrives, you get told which subsets of
the elements so far are independent, but not more. In this case, an online algorithm
can be fooled regardless for any n≥3 (even with linearly realisable matroids); see page 9 of
Click to access 1312.5953.pdf
This leads to a question that I think might prove tractable: determine
the maximal number f(n)<n (n≥3) such that there exists an online
algorithm in scenario (2) for arranging f(n) bases, but not for arranging
f(n)+1 bases. E.g., does f(n) grow as a square root of n?
Comment by Jan Draisma — March 7, 2017 @ 3:57 pm |
No, I’m pretty sure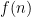 is linear, at least
is linear, at least  and at most
and at most 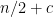 . Indeed you can do
. Indeed you can do 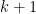 bases in
bases in  dimensions (at least for linearly realisable matroids), but you can’t do them in
dimensions (at least for linearly realisable matroids), but you can’t do them in  dimensions.
dimensions.
For the lower bound, you simply use an extension of the argument from the linked paper above: There exist vectors for
for  and
and 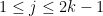 such that they are in general position (i.e. any
such that they are in general position (i.e. any  of them are linearly independent), but the vectors
of them are linearly independent), but the vectors 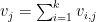 for
for 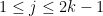 are the same (non-zero) vector. (Proof: fix a prime
are the same (non-zero) vector. (Proof: fix a prime 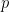 that is greater than
that is greater than
 , and choose the sum
, and choose the sum  and the vectors
and the vectors  with
with 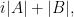 then at least one of
then at least one of  and
and  can be extended by some element of
can be extended by some element of 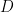 .
.
This is true for linearly realisable matroids because the space generated by the union of and
and  is of dimension at least
is of dimension at least  , so the intersection of the spaces generated by
, so the intersection of the spaces generated by  and by
and by  is of dimension at most
is of dimension at most  , so is less than
, so is less than  , so there is some element of
, so there is some element of 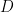 that is not in the intersection of those spaces, so there is some element of
that is not in the intersection of those spaces, so there is some element of 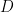 that is either not in the space generated by
that is either not in the space generated by  or the space generated by
or the space generated by  .
.
So our strategy in dimension is: when the
dimension is: when the  th basis arrives (for
th basis arrives (for  ), make it so the first
), make it so the first  sets of 4 columns each form an independent set of size
sets of 4 columns each form an independent set of size 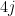 , and then use Hall’s Basis Theorem to make the other columns all be independent.
, and then use Hall’s Basis Theorem to make the other columns all be independent.
It is clear by the basis exchange axiom that we can make the first sets of 4 columns each form an independent set of size
sets of 4 columns each form an independent set of size 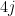 (we start with an independent set of size
(we start with an independent set of size  and have
and have 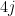 independent vertices to choose from).
independent vertices to choose from).
For the remainder, we have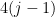 columns (of
columns (of 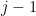 vectors each) of which the first pair of pairs of columns both make a matroid of dimension at least
vectors each) of which the first pair of pairs of columns both make a matroid of dimension at least  , the next pair of pairs of columns both make a matroid of dimension at least
, the next pair of pairs of columns both make a matroid of dimension at least 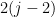 , and so on until the final pair of pairs of columns both make a matroid of dimension at least 2.
, and so on until the final pair of pairs of columns both make a matroid of dimension at least 2.
Create a bipartite graph with partition of the
of the 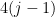 columns and
columns and 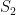 of the
of the 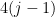 vectors we need to add in from the latest basis, where an edge exists if the column and the vector make an independent set (of size
vectors we need to add in from the latest basis, where an edge exists if the column and the vector make an independent set (of size  ).
).
Each vertex in makes a matroid of dimension
makes a matroid of dimension 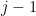 , so there are at least
, so there are at least  of the vertices in
of the vertices in 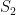 adjacent. In particular if
adjacent. In particular if 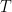 is a subset of
is a subset of  is of size at most
is of size at most  , the total number of neighbours of
, the total number of neighbours of 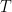 is at least
is at least  . If, on the other hand,
. If, on the other hand, 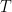 is of size
is of size 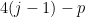 where
where  , it includes both columns from one of the first
, it includes both columns from one of the first  pairs of columns, so it includes two pairs of columns which together make a matroid of dimension at most
pairs of columns, so it includes two pairs of columns which together make a matroid of dimension at most  . So these two columns (let’s call them
. So these two columns (let’s call them  and
and  ) are of size
) are of size 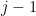 , and their union contains a set
, and their union contains a set 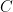 of size
of size  , so if
, so if 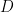 is any set of size more than
is any set of size more than 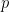 , either
, either  or
or  is extendible by an element of
is extendible by an element of 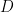 . In particular, there are at most
. In particular, there are at most 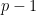 elements of
elements of 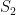 which are not adjacent to either
which are not adjacent to either  or
or  , so there are at least
, so there are at least  neighbours of
neighbours of 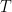 .
.
So the conditions of Hall’s Marriage Theorem apply, and we can add the remaining vectors of the basis to the matrix and make each column independent.
My instincts are that this proof can be improved to actually show that you can do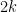 , solving the problem completely. I did this for
, solving the problem completely. I did this for  , but couldn’t quite do so for
, but couldn’t quite do so for 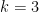 .
.
Comment by Luke Pebody — March 25, 2017 @ 5:38 pm |
If someone can edit this to make the latex things work, that would be very welcome. It seems to have caused a huge gap including the end of the proof of the upper bound and the start of the proof of the lower bound. Is there a ‘preview my post’ feature?
Comment by Luke Pebody — March 25, 2017 @ 5:43 pm |
I tried to fix your LaTeX; hopefully this is what you wanted. I’m new to WordPress myself so I am not aware of a “preview” feature; I agree that that would be nice.
Comment by tchow8 — March 26, 2017 @ 9:16 pm |
Thanks Tim, that looks a lot better.
It has occurred to me the Lemma I needed (if A, B, C and D are independent sets in a matroid with C contained in and with |C|+|D|>|A|+|B| then either A or B can be extended by some element of D) is true by the submodularity of the rank function applied to
and with |C|+|D|>|A|+|B| then either A or B can be extended by some element of D) is true by the submodularity of the rank function applied to 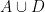 and
and  .
.
The rank of the intersection of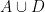 and
and  is at least |D| clearly, and the rank of their union is at least |C|. It follows that the sum of their ranks is more than |A|+|B|, and hence either the rank of
is at least |D| clearly, and the rank of their union is at least |C|. It follows that the sum of their ranks is more than |A|+|B|, and hence either the rank of 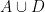 is more than |A| (and hence A is not a maximal independent set in
is more than |A| (and hence A is not a maximal independent set in 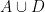 ) or the rank of
) or the rank of  is more than |B| (and hence B is not a maximal independent set in
is more than |B| (and hence B is not a maximal independent set in  ).
).
Comment by Luke Pebody — March 26, 2017 @ 9:57 pm |
Since this turned out pretty unreadable, I threw together some latex of the two proofs at https://www.overleaf.com/8773999gccdbdmfdgkm
Comment by Luke Pebody — March 26, 2017 @ 4:36 pm |
Pretty sure the same proof works to show you can do k+1 bases in 3k dimensions. What I’m using the groups of 4 for is that if you remove 0 or 1 columns, there’s still a pair remaining that works together. The same would be true with groups of 3.
Comment by Luke Pebody — March 26, 2017 @ 5:12 pm |
So I think it might be possible to extend this method to fully solve the question for online matroids.
I feel that the answer is that you can do k + 1 bases in rank 2k, but can’t necessarily do them in rank 2k-1. So far it is proved you can in rank 3k and can’t in rank 2k-1.
In order to place the (k+1)’th basis, it is sufficient to achieve that some 2 columns so far together have rank 2k, that if you cover up any column there are 2 columns remaining that together have rank at least 2k-1, that if you cover up any 2 columns there are 2 columns remaining that together have rank at least 2k-2 and so on (up to if you cover up any k-2 columns there are 2 columns remaining that together have rank at least k+2).
We stop at k-2, because it is trivial that if you cover up any k-1 columns there are 2 columns remaining that together have rank at least k+1: otherwise in the remaining k x (k+1) grid all the columns are maximal independent sets and all the rows are larger independent sets.
For k=2, you want to achieve that some 2 columns have rank 4, which is trivial to achieve in rank 4 by extending independent sets..
For k=3, you want to achieve both that some 2 columns have dimension 6 (trivial in rank 6 by extending independent sets) and also that if you cover up any column, some 2 uncovered columns have rank at least 5. Wondering if maybe someone can see how to achieve this in rank 6? (Or prove it can’t always be done)
In particular, for any k, we would be done if we could achieve that after the k’th basis, we can find k disjoint pairs of columns such that one pair combined has rank 2k, one pair has rank 2k-1, one pair has rank 2k-2, …, one pair has rank k+1. Maybe you can even arrange it so you can find k disjoint pairs of columns such that each pair combined has rank 2k?
Comment by Luke Pebody — March 28, 2017 @ 6:14 am |
I haven’t gotten around to studying your argument yet, but I just wanted to say that fully solving the question for online matroids would be an excellent partial result and I hope that others will jump in to help.
Comment by tchow8 — March 28, 2017 @ 3:08 pm |
So far I could only digest the lower bound. I think it might be useful to summarize it as follows. In an n-dimensional space, we pick a line, and n subspaces of dimension n/2 that all contain it, but are otherwise generic. For each subspace, take n/2 generating vectors. Then any n of these n x n/2 vectors are independent. So if we get them in a matrix as n/2 rows of length n, we can do nothing but randomly put them in columns. If we are unlucky, we might just group them exactly such that each column generates one of the n/2-dimensional subspaces. But then if the next row we get contains a vector from the line they have in common, we are #$&!ed.
Comment by domotorp — March 29, 2017 @ 11:25 am |
Yes, except that the dimension of the subspaces must be less than n/2, in order for the statement ‘any n of these n by subspaces are independent’ to be true.
Comment by Luke Pebody — March 31, 2017 @ 6:25 am |
Regarding the upper bound, I think one could use some form of Hall’s theorem. For example, suppose that we could arrange the first k rows (of length 2k) such that any line is contained in at most k of the 2k k-dimensional subspaces generated by the columns. Construct a bipartite graph where one class is the collection of these 2k subspaces, while the other class is the 2k vectors of the (k+1)-th basis, and a vector is connected to a subspace if it’s not contained in it. Then the above condition would be sufficient to find a perfect matching. Unfortunately this condition is not always true, but probably we can guarantee it with some care when arranging the first k rows.
Comment by domotorp — March 30, 2017 @ 7:40 am |
This is coming to an earlier question of Jordan-in what way could this conjecture made more general. I propose the following: Take any by
by  array of nonzero vectors such that for any
array of nonzero vectors such that for any  no matter how we pick
no matter how we pick  vectors from distinct rows on each of the remaining rows we can find a vector not in their span. This is easily checked out by having bases on each of the rows or having the example of a vectors linearly independent on the first column and linear multiple of each of them on the rows.
vectors from distinct rows on each of the remaining rows we can find a vector not in their span. This is easily checked out by having bases on each of the rows or having the example of a vectors linearly independent on the first column and linear multiple of each of them on the rows. -partite graph on the rows and draw an edge between the vertices in different parts if they are independent. Rota would say that each vertex is connected to at least
-partite graph on the rows and draw an edge between the vertices in different parts if they are independent. Rota would say that each vertex is connected to at least  vertices in any other part and then we want to find n disjoints paths through the parts of the graph. Jordan’s example is even more rich in edges, every vertex has degree
vertices in any other part and then we want to find n disjoints paths through the parts of the graph. Jordan’s example is even more rich in edges, every vertex has degree  .
.
One motivation for this is: we draw an
The condition stated above seems very reminiscent of the marriage lemma condition.
Comment by VladM — March 7, 2017 @ 7:19 pm |
Once again, this fails on Colin McDiarmid’s example. Denote the edges of by
by 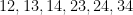 and create duplicates
and create duplicates  of three of the edges. Then the sets
of three of the edges. Then the sets  ,
,  , and
, and 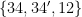 satisfy your condition but the conclusion of Rota’s Basis Conjecture fails.
satisfy your condition but the conclusion of Rota’s Basis Conjecture fails.
I think it is going to be difficult to formulate a satisfactory generalization of this type without coming to grips with the “local obstructions” that I mentioned above.
Comment by tchow8 — March 7, 2017 @ 7:30 pm |
On Matroids with No Small Circuits.
A paving matroid is one in which the sets of size less than the rank are
all independent. With Peter Humphries I proved that:
Theorem. be disjoint sets of size
be disjoint sets of size 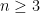 , and let
, and let
 be rank
be rank  paving matroids on
paving matroids on 
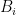 is a basis of
is a basis of 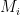 for each
for each  .
. disjoint transversals
disjoint transversals  of
of
 such that
such that 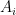 is a basis of
is a basis of 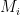 for each
for each
 .
.
Let
such that
Then there exist
This strengthening of Rota’s Basis Conjecture fails for matroids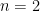 for paving matroids. After an unpleasant
for paving matroids. After an unpleasant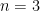 case, the result
case, the result
in general and for
case analysis establishing the result for the
is proved by an easy inductive argument.
Tim is proposing extending the results in our paper, for any fixed
 , to rank-
, to rank- matroids in which the
matroids in which the  -element sets are
-element sets are is large relative
is large relative . To prove such a result one would likely need to do a lot
. To prove such a result one would likely need to do a lot , but then the induction
, but then the induction
all independent. It could well be true that the above theorem itself
would hold for such matroids so long as
to
of work to establish it for some value of
should be easy.
I don’t see this leading to a full proof of Rota’s Basis Conjecture,
but it is a concrete approach toward interesting partial results.
On a related note, it is conjectured that the proportion of -element
-element goes to infinity. Given the
goes to infinity. Given the
matroids that are paving tends to one as
exciting new results of Jorn van der Pol and Rudi Pendavingh on the
structure of almost all matroids one might be able to prove that
Rota’s Basis Conjecture (for matroids) is almost always true.
Comment by Jim Geelen — March 7, 2017 @ 8:56 pm |
I have been reading the Geelen-Humphries paper and I would like to explain here the idea behind their induction step, which is the part of their argument that I think is most valuable if we are thinking of extending the results.
The starting point is the observation that in Rota’s Basis Conjecture, it is easy to arrange for the first column of the grid to be a basis. It is then natural to imagine covering up the first row and column and applying some kind of induction hypothesis to the remaining grid. However, several issues arise if we try to do this naively. First of all, the rows of the
grid. However, several issues arise if we try to do this naively. First of all, the rows of the  grid aren’t bases of an
grid aren’t bases of an 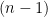 -dimensional vector space; they’re still sitting inside an
-dimensional vector space; they’re still sitting inside an  -dimensional vector space. Secondly, and more seriously, even if we were to get the columns of the
-dimensional vector space. Secondly, and more seriously, even if we were to get the columns of the  grid to all be linearly independent, there’s no guarantee that when we return to the original grid and add back the vector
grid to all be linearly independent, there’s no guarantee that when we return to the original grid and add back the vector  from the first row, the
from the first row, the  th column will still be linearly independent.
th column will still be linearly independent.
The first idea that Geelen and Humphries have to try to address these problems is contraction. For those not familiar with matroid theory, contraction may be thought of as orthogonal projection: If is a set of nonzero vectors in a real vector space and
is a set of nonzero vectors in a real vector space and  , then the contraction of
, then the contraction of  by
by  (written
(written 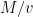 ) is obtained by orthogonally projecting all the vectors of
) is obtained by orthogonally projecting all the vectors of  onto the hyperplane perpendicular to
onto the hyperplane perpendicular to  , and deleting
, and deleting  itself (which has been projected to zero, of course). This has the effect of reducing the rank by one, and also has the nice property that if we take any basis of the contraction and add back the original vector
itself (which has been projected to zero, of course). This has the effect of reducing the rank by one, and also has the nice property that if we take any basis of the contraction and add back the original vector  , we get a basis for the original vector space. In Rota’s Basis Conjecture, the idea is that for each column
, we get a basis for the original vector space. In Rota’s Basis Conjecture, the idea is that for each column  , we contract by
, we contract by  . This (seemingly) addresses both issues in the previous paragraph.
. This (seemingly) addresses both issues in the previous paragraph.
However, in the process of seemingly solving these issues, we’ve introduced new issues. The vectors in the first row are all distinct (in fact, linearly independent) so contracting by can give a totally different result from contracting by
can give a totally different result from contracting by 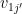 if
if  . This is why Geelen and Humphries end up proving something about
. This is why Geelen and Humphries end up proving something about  different matroid structures on the same ground set. Another issue is, if we contract by
different matroid structures on the same ground set. Another issue is, if we contract by  , how do we know that we’ll get a basis (for the contraction) in the
, how do we know that we’ll get a basis (for the contraction) in the  th row? We somehow need to ensure that if we combine
th row? We somehow need to ensure that if we combine  with the vectors
with the vectors  , the result is a basis of the original space.
, the result is a basis of the original space.
This latter condition is something that Geelen and Humphries state explicitly as a lemma, and prove using the assumption that we are dealing with paving matroids. Namely, they prove that if there are no linearly dependent sets of size less than (actually, as mentioned in the previous paragraph, they prove this for
(actually, as mentioned in the previous paragraph, they prove this for  different paving matroid structures on the ground set, but I’ll ignore this for simplicity), then it is possible to find
different paving matroid structures on the ground set, but I’ll ignore this for simplicity), then it is possible to find  for all
for all  so that
so that 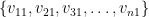 is a basis and also
is a basis and also  is a basis for all
is a basis for all  .
.
The interesting thing about this lemma is that it is a type of basis exchange property. We’re starting with bases and then we’re simultaneously swapping out
bases and then we’re simultaneously swapping out  elements from the first basis with one element from each of the other bases in a way that leaves everything a basis at the end. As indicated above, this particular basis exchange property does not hold in full generality, but relies on the assumption that there are no small linearly dependent sets. Geelen and Humphries prove this lemma by induction. Here I want to focus not on the induction step of this argument, but on the argument that lets them prove the base case, because it illustrates something that I think is of general interest for Rota’s Basis Conjecture.
elements from the first basis with one element from each of the other bases in a way that leaves everything a basis at the end. As indicated above, this particular basis exchange property does not hold in full generality, but relies on the assumption that there are no small linearly dependent sets. Geelen and Humphries prove this lemma by induction. Here I want to focus not on the induction step of this argument, but on the argument that lets them prove the base case, because it illustrates something that I think is of general interest for Rota’s Basis Conjecture.
The key claim is the following: Suppose we have a matroid with no dependent sets of size less than , where
, where  . Let
. Let  and
and 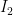 be two disjoint independent sets of size
be two disjoint independent sets of size  , and let
, and let  be any subset of
be any subset of  of size 2 and let
of size 2 and let 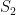 be any subset of
be any subset of 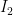 of size 3. Then there exists
of size 3. Then there exists 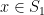 and
and  such that if we “swap”
such that if we “swap”  and
and 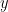 , then the resulting sets
, then the resulting sets  and
and 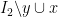 are independent.
are independent.
How do we prove this claim? First we note the following: Denote the two elements of by
by  and
and 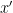 , and let
, and let 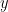 be arbitrary; then we claim that either
be arbitrary; then we claim that either  or
or  is independent. For if not, they are both linearly dependent, and since there are no dependent sets of size less than
is independent. For if not, they are both linearly dependent, and since there are no dependent sets of size less than  , they are both circuits (minimal dependent sets). They are distinct and both contain
, they are both circuits (minimal dependent sets). They are distinct and both contain 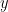 , so by the circuit elimination axiom of matroid theory, their union, minus
, so by the circuit elimination axiom of matroid theory, their union, minus 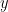 , must contain a circuit. But their union minus
, must contain a circuit. But their union minus 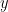 is a subset of
is a subset of  itself, which is independent; contradiction. So, either
itself, which is independent; contradiction. So, either  or
or  is independent. Now apply this argument to each element
is independent. Now apply this argument to each element 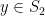 in turn; by the pigeonhole principle, there must be some
in turn; by the pigeonhole principle, there must be some  such that both
such that both  and
and  are independent (or else this claim holds for
are independent (or else this claim holds for 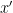 , but without loss of generality we may assume that it is
, but without loss of generality we may assume that it is  ). Then, applying the argument at the beginning of this paragraph with
). Then, applying the argument at the beginning of this paragraph with 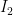 in place of
in place of  and
and  in place of
in place of  , we can infer that for one of
, we can infer that for one of  or
or  —and without loss of generality we may assume it is
—and without loss of generality we may assume it is  —we must have
—we must have  is independent as well.
is independent as well.
The reason I think the argument in the previous paragraph is interesting is that it can be interpreted as saying that the absence of small circuits implies a weak form of base-orderability. Base-orderability is, I think, a crucial concept for the conjecture; it is known that strongly base-orderable matroids not only satisfy Rota’s Basis Conjecture but also have no local obstructions, so they satisfy various strengthenings of the conjecture. I may say something more about this later, but this comment is already long enough!
Comment by tchow8 — March 9, 2017 @ 5:16 pm |
The argument seems correct, except that it seems that half of the time you wrote independent instead of dependent; so in the claim, we need to suppose that there is no dependent set of size less than . Also, let me remark that it might be better to suppose from the beginning that
. Also, let me remark that it might be better to suppose from the beginning that  and
and 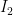 are disjoint (otherwise the statement is not necessarily true).
are disjoint (otherwise the statement is not necessarily true).
Comment by domotorp — March 9, 2017 @ 9:06 pm |
I fixed the dependent/independent typos; thanks!
What’s a counterexample when and
and 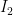 are not disjoint?
are not disjoint?
Comment by tchow8 — March 9, 2017 @ 10:54 pm |
If and
and  .
.
Comment by domotorp — March 10, 2017 @ 9:11 am |
Ah, I see. Technically, and
and 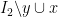 are independent in this case as well, but they now have smaller cardinality than the original independent sets, and the term “swap” is misleading, so I agree that it is better to specify that
are independent in this case as well, but they now have smaller cardinality than the original independent sets, and the term “swap” is misleading, so I agree that it is better to specify that  and
and 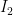 are disjoint.
are disjoint.
Comment by tchow8 — March 20, 2017 @ 4:59 pm |
I think that the prospects for generalizing Geelen–Humphries are good. Here are some thoughts.
Definition. Let be a non-negative integer. Say that a matroid of rank
be a non-negative integer. Say that a matroid of rank  is
is  -paving if it has no circuits of size less than
-paving if it has no circuits of size less than  .
.
Thus a 0-paving matroid is a uniform matroid and a 1-paving matroid is a paving matroid in the usual sense. I believe that it is straightforward to prove the following Proposition (though it would be good for someone to verify):
Proposition. For any fixed , the class of
, the class of  -paving matroids is minor-closed; i.e., if you delete or contract an element of a
-paving matroids is minor-closed; i.e., if you delete or contract an element of a  -paving matroid, the result is a
-paving matroid, the result is a  -paving matroid.
-paving matroid.
My first thought is that it is natural to try to generalize the Geelen–Humphries result to -paving matroids.
-paving matroids.
A second observation is that, as I alluded to an in earlier comment, a key lemma in their paper is the following:
Key Lemma. Let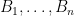 be disjoint sets of size
be disjoint sets of size 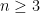 , and let
, and let 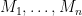 be rank-
be rank- paving matroids on
paving matroids on  such that
such that 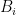 is a basis of
is a basis of 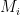 for each
for each  . Then there is an ordering of the elements of
. Then there is an ordering of the elements of 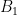 as
as 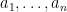 and a transversal
and a transversal  of
of  such that the set
such that the set  is a basis of
is a basis of 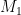 , and for all
, and for all 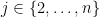 ,
,  is a basis of
is a basis of  .
.
One thing that I realized recently is that if all the matroids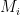 are identical, with
are identical, with 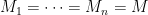 say, then the Key Lemma holds for any matroid
say, then the Key Lemma holds for any matroid  , not just paving matroids. This follows from the following result, which I believe was first proved in “Comments on bases in dependence structures” by Richard Brualdi, Bull. Austral. Math. Soc. 1 (1969), 161–167.
, not just paving matroids. This follows from the following result, which I believe was first proved in “Comments on bases in dependence structures” by Richard Brualdi, Bull. Austral. Math. Soc. 1 (1969), 161–167.
Strong Basis Exchange. If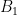 and
and 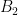 are bases of a matroid, then for any
are bases of a matroid, then for any  there exists
there exists 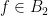 such that both
such that both 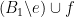 and
and  are bases.
are bases.
To prove the Key Lemma when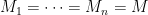 , use Strong Basis Exchange to swap each
, use Strong Basis Exchange to swap each 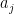 in turn with some
in turn with some  , as
, as  runs from 2 to
runs from 2 to  .
.
I think that the Key Lemma is false in general if the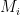 are not all identical and are not all paving matroids (though I don’t have a counterexample offhand; maybe someone else can construct one). Certainly Brualdi’s proof breaks down. However, I suggest the following plan: Tinker with the statement of the Key Lemma, as well as the statement of the Theorem in Geelen’s comment above, to get the induction step of Geelen–Humphries to work for a more general class of matroids than paving matroids (perhaps
are not all identical and are not all paving matroids (though I don’t have a counterexample offhand; maybe someone else can construct one). Certainly Brualdi’s proof breaks down. However, I suggest the following plan: Tinker with the statement of the Key Lemma, as well as the statement of the Theorem in Geelen’s comment above, to get the induction step of Geelen–Humphries to work for a more general class of matroids than paving matroids (perhaps  -paving matroids, or perhaps an even more general class of matroids). This seems eminently doable to me. Of course, even if this plan succeeds, it doesn’t prove much by itself in the absence of a proof of the base case. But I think it would be an important step forwards.
-paving matroids, or perhaps an even more general class of matroids). This seems eminently doable to me. Of course, even if this plan succeeds, it doesn’t prove much by itself in the absence of a proof of the base case. But I think it would be an important step forwards.
Comment by tchow8 — March 20, 2017 @ 6:16 pm |
Here are some further thoughts about the “tinkering” I mentioned above.
Suppose that we modify the Theorem in Geelen’s comment by replacing “paving matroid” with “2-paving matroid.” I don’t know if this modified assertion is true, but suppose we try to prove it using similar methods. If I haven’t made a mistake, the class of 2-paving matroids is minor-closed, so the same strategy, of using contraction to reduce to a smaller instance, has a fighting chance of working. In fact, I think that if the Key Lemma holds for 2-paving matroids then the inductive step (though not necessarily the base case) of the proof of the Theorem should go through.
However, some trouble arises when we try to prove the Key Lemma by mimicking the argument of Geelen and Humphries. I think you can only conclude that if you pick any three elements of a basis then you can swap one of them out with an element of a disjoint basis of another 2-paving matroid (provided that the rank is at least seven), and this lets you get to be a basis as well as
to be a basis as well as  to be a basis for
to be a basis for 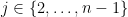 , but then you get stuck at the last step
, but then you get stuck at the last step 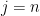 .
.
Now maybe the Key Lemma is still true, and one just needs a different argument. On the other hand, here’s another possible diagnosis of what’s going wrong: We know that the Key Lemma is true for all matroids when all the matroid structures are equal, and what’s causing us trouble is that we’re trying to prove it for a whole sequence of distinct matroid structures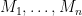 . It seems difficult to avoid considering different matroid structures on the same ground set if we stick to the strategy of contracting a different vector for each column. Nevertheless, from the point of view of Rota’s Basis Conjecture, we don’t necessarily need to prove the Key Lemma for arbitrary
. It seems difficult to avoid considering different matroid structures on the same ground set if we stick to the strategy of contracting a different vector for each column. Nevertheless, from the point of view of Rota’s Basis Conjecture, we don’t necessarily need to prove the Key Lemma for arbitrary 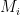 . For example, the
. For example, the 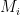 that arise in the (purported) inductive proof of Rota’s Basis Conjecture are all minors of the same initial matroid. So maybe what we need to do is to narrow our sights a little and only try to prove the Key Lemma for matroids
that arise in the (purported) inductive proof of Rota’s Basis Conjecture are all minors of the same initial matroid. So maybe what we need to do is to narrow our sights a little and only try to prove the Key Lemma for matroids 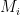 that enjoy some degree of similarity, that is preserved when we perform certain sequences of deletions and contractions from the same starting matroid. By the same token, the Theorem itself might need to be similarly narrowed. These narrowings might make the Key Lemma (and the Theorem) easier to prove, yet still general enough to imply Rota’s Basis Conjecture.
that enjoy some degree of similarity, that is preserved when we perform certain sequences of deletions and contractions from the same starting matroid. By the same token, the Theorem itself might need to be similarly narrowed. These narrowings might make the Key Lemma (and the Theorem) easier to prove, yet still general enough to imply Rota’s Basis Conjecture.
Comment by tchow8 — March 21, 2017 @ 8:44 pm |
Question. Let be a base-orderable matroid with ground set
be a base-orderable matroid with ground set 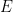 , and let
, and let  . Let
. Let 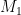 and
and 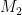 be matroid structures on
be matroid structures on  , each of which is obtained by a sequence of deletions and contractions of the elements of
, each of which is obtained by a sequence of deletions and contractions of the elements of  (but not necessarily the same sequence of deletions and contractions; so although
(but not necessarily the same sequence of deletions and contractions; so although 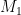 and
and 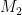 are both minors of
are both minors of  and have the same ground set
and have the same ground set  , they are not necessarily isomorphic). Suppose further that
, they are not necessarily isomorphic). Suppose further that 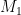 and
and 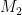 have the same rank. Is it necessarily the case that if
have the same rank. Is it necessarily the case that if 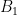 is a basis of
is a basis of 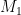 and
and 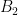 is a basis of
is a basis of 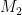 , then there exists a bijection
, then there exists a bijection  such that for all
such that for all  ,
,  is a basis of
is a basis of 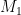 and
and  is a basis of
is a basis of 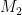 ?
?
It is plausible to me that the answer is yes. For example, note that an independent set of a minor is independent in the original matroid, so both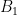 and
and 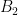 are necessarily independent in
are necessarily independent in  . It seems plausible that we could extend both of them to bases in
. It seems plausible that we could extend both of them to bases in  , use the base-orderability of
, use the base-orderability of  to get a bijection, and then restrict the bijection. Or something like that.
to get a bijection, and then restrict the bijection. Or something like that.
If the answer is yes, then I think that the Geelen–Humphries induction argument goes through for base-orderable matroids. In the Theorem of Geelen’s comment above, we replace “paving matroid” by “base-orderable matroid,” and we also require that all matroid structures arise from a sequence of deletions and contractions from the same starting matroid. We modify the Key Lemma similarly. The Key Lemma then follows from a positive answer to the Question, because we can swap each
matroid structures arise from a sequence of deletions and contractions from the same starting matroid. We modify the Key Lemma similarly. The Key Lemma then follows from a positive answer to the Question, because we can swap each 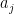 in turn with some
in turn with some  as
as  runs from 2 to
runs from 2 to  . Then we can apply the induction hypothesis to the contractions
. Then we can apply the induction hypothesis to the contractions 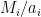 restricted to the set
restricted to the set 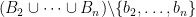 .
.
Comment by tchow8 — March 29, 2017 @ 1:23 am |
Unfortunately, the answer to the Question is no. Let be the matroid associated with the graph that is a disjoint union of two triangles
be the matroid associated with the graph that is a disjoint union of two triangles  and
and 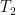 . Choose
. Choose  and
and  , and let
, and let 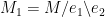 and let
and let  . Then all these matroids are base-orderable, and
. Then all these matroids are base-orderable, and 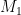 and
and 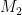 are even abstractly isomorphic (but not equal), but it is easy to check that the desired bijection
are even abstractly isomorphic (but not equal), but it is easy to check that the desired bijection  does not necessarily exist.
does not necessarily exist.
Comment by tchow8 — March 29, 2017 @ 5:51 pm |
The Key Lemma is not true for all “2 paving matroids”. In particular, the rank of could be n-2 in
could be n-2 in 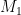 .
.
Comment by Luke Pebody — April 2, 2017 @ 7:33 am |
Let me say a bit more about base-orderability. A matroid is strongly base-orderable if, for any two bases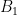 and
and 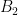 , there exists a bijection
, there exists a bijection  such that for any subset
such that for any subset  , the set
, the set  is a basis. It is not hard to show that this axiom implies that
is a basis. It is not hard to show that this axiom implies that  is also a basis. Strong base-orderability is a very strong condition. We have the following result:
is also a basis. Strong base-orderability is a very strong condition. We have the following result:
Proposition. Let be a strongly base-orderable matroid of rank
be a strongly base-orderable matroid of rank  with
with 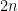 elements, and suppose that there exists a partition of
elements, and suppose that there exists a partition of  into
into  disjoint bases. Given any
disjoint bases. Given any  disjoint independent sets
disjoint independent sets  with
with 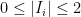 , there exists an
, there exists an 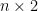 grid such that the elements of
grid such that the elements of  appear in row
appear in row  and such that both columns are bases of
and such that both columns are bases of  .
.
Sketch of proof: Let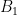 and
and 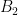 be disjoint bases of
be disjoint bases of  . Denote the elements of
. Denote the elements of 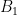 by
by 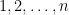 . Let
. Let  be the the bijection guaranteed by strong base-orderability, and write
be the the bijection guaranteed by strong base-orderability, and write 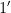 for
for  ,
,  for
for  , etc. Construct any
, etc. Construct any 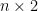 grid such that the elements of
grid such that the elements of  appear in row
appear in row  . Then a Hall’s marriage theorem argument along the lines of Proof 2 of Theorem 1 in this paper shows that we can permute the elements within each row so that both columns contain the numbers
. Then a Hall’s marriage theorem argument along the lines of Proof 2 of Theorem 1 in this paper shows that we can permute the elements within each row so that both columns contain the numbers  through
through  if we erase the primes. Strong base-orderability implies that the two columns must be bases.
if we erase the primes. Strong base-orderability implies that the two columns must be bases.
Theorem 4 of this paper then implies that the generalization of the above Proposition with replaced by any larger number is also true, and so this yields a proof of Wild’s theorem that Rota’s Basis Conjecture holds for strongly base-orderable matroids.
replaced by any larger number is also true, and so this yields a proof of Wild’s theorem that Rota’s Basis Conjecture holds for strongly base-orderable matroids.
As already discussed in earlier comments, there are local obstructions (such as and
and 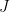 ) that prevent the above Proposition from being true in general. The point is that these local obstructions vanish in the presence of strong base-orderability. Thus if we wish to search for local obstructions, we should look at non-base-orderable matroids. Another way to think about it is that if we want to generalize Wild’s theorem, we might want to look at weaker base-orderability hypotheses and see how far we can get with them. A very optimistic, but not inconceivable, route to proving Rota’s Basis Conjecture would be to formulate a generalization to
) that prevent the above Proposition from being true in general. The point is that these local obstructions vanish in the presence of strong base-orderability. Thus if we wish to search for local obstructions, we should look at non-base-orderable matroids. Another way to think about it is that if we want to generalize Wild’s theorem, we might want to look at weaker base-orderability hypotheses and see how far we can get with them. A very optimistic, but not inconceivable, route to proving Rota’s Basis Conjecture would be to formulate a generalization to 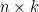 grids that has some kind of weak base-orderability hypothesis
grids that has some kind of weak base-orderability hypothesis 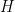 with two properties: (1) when
with two properties: (1) when 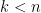 ,
, 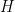 blocks annoying counterexamples like
blocks annoying counterexamples like  and
and 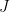 , and (2) when
, and (2) when  ,
, 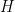 is automatically satisfied by all matroids.
is automatically satisfied by all matroids.
Administrative note: I will be unavailable to participate in Polymath for the next week or so. Obviously, this should not prevent others from continuing to work.
Comment by tchow8 — March 10, 2017 @ 12:00 am |
Here is another thought about base-orderability. A matroid is said to be base-orderable (note that I have dropped the adverb “strongly”) if for any two bases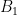 and
and 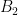 , there exists a bijection
, there exists a bijection  such that for every
such that for every 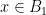 , the sets
, the sets  and
and  are both bases. The following theorem is proved in J. de Sousa and D. J. A. Welsh, “A characterisation of binary transversal structures,” J. Math. Anal. Appl. 40 (1972), 55–59.
are both bases. The following theorem is proved in J. de Sousa and D. J. A. Welsh, “A characterisation of binary transversal structures,” J. Math. Anal. Appl. 40 (1972), 55–59.
Theorem. A binary matroid (i.e., a matroid representable by vectors in a vector space over the field with two elements) is base-orderable if and only if it contains no minor.
minor.
As we have seen, base-orderability (or at least strong base-orderability) makes life easier for the would-be prover of Rota’s Basis Conjecture. So one could imagine a strategy for proving Rota’s Basis Conjecture for binary matroids that proceeds along the following lines: When base-orderability seems to be useful, split into two cases. In Case A, go ahead and assume base-orderability. In Case B, exploit the above theorem to conclude that there must be a minor lying around somewhere, and do something special to take care of it.
minor lying around somewhere, and do something special to take care of it.
Comment by tchow8 — March 21, 2017 @ 9:01 pm |
After studying the literature a bit more, I learned that binary matroids that contain no minor are the same as series-parallel matroids, and in particular are strongly base-orderable (because strong base-orderability is closed under series and parallel connection). Thus Rota’s Basis Conjecture is known to be true for binary matroids with no
minor are the same as series-parallel matroids, and in particular are strongly base-orderable (because strong base-orderability is closed under series and parallel connection). Thus Rota’s Basis Conjecture is known to be true for binary matroids with no  minor.
minor.
This suggests to me that binary matroids are a good testing ground for proof strategies that involve grappling with what I’ve been calling “local obstructions.” In some sense, is the only local obstruction that we have to worry about for binary matroids; we don’t have to worry about
is the only local obstruction that we have to worry about for binary matroids; we don’t have to worry about 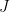 (which is not binary) or any other unknown local obstructions.
(which is not binary) or any other unknown local obstructions.
Comment by tchow8 — April 8, 2017 @ 3:56 am |
To be a little less vague, here is an outline of a possible strategy for proving Rota’s Basis Conjecture for binary matroids. Recall that strongly base-orderable matroids satisfy an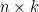 version of the conjecture: If we have
version of the conjecture: If we have  disjoint independent sets of size
disjoint independent sets of size  , whose union can be partitioned into
, whose union can be partitioned into  disjoint bases, then there is an
disjoint bases, then there is an 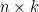 grid whose rows are the given independent sets and whose columns are all bases. So for binary matroids, we could imagine constructing the first
grid whose rows are the given independent sets and whose columns are all bases. So for binary matroids, we could imagine constructing the first  columns of our desired
columns of our desired 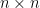 grid (for some hopefully not-too-large value of
grid (for some hopefully not-too-large value of  ) in such a way that the remaining
) in such a way that the remaining 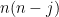 elements contain no
elements contain no  minor (and therefore comprise a strongly base-orderable matroid); then as long as these
minor (and therefore comprise a strongly base-orderable matroid); then as long as these 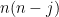 elements can be partitioned into
elements can be partitioned into 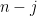 disjoint bases, we will be done.
disjoint bases, we will be done.
Of course, this plan requires us to get a handle on how many minors there can be in a binary matroid. So, as a preliminary step, let me pose this question. If
minors there can be in a binary matroid. So, as a preliminary step, let me pose this question. If  is a binary matroid, let
is a binary matroid, let 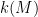 denote the minimum number of elements we have to delete from
denote the minimum number of elements we have to delete from  to produce a
to produce a  -minor-free matroid. Abusing notation slightly, for every positive integer
-minor-free matroid. Abusing notation slightly, for every positive integer  , let
, let  where the maximum is over all binary matroids
where the maximum is over all binary matroids  with
with  elements. What can we say about how big
elements. What can we say about how big  is?
is?
Comment by tchow8 — April 8, 2017 @ 3:58 pm |
I think that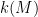 can be as large as
can be as large as  already for binary matroids. This is because a
already for binary matroids. This is because a  minor free graph can have at most
minor free graph can have at most  edges. So if the
edges. So if the  elements are arranged to form all edges of a complete graph on
elements are arranged to form all edges of a complete graph on 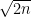 vertices, we get
vertices, we get  .
.
Comment by domotorp — April 8, 2017 @ 8:45 pm |
Can you please explain why a -minor-free (simple?) graph can have at most
-minor-free (simple?) graph can have at most  edges?
edges?
Comment by tchow8 — April 10, 2017 @ 2:19 pm |
Hadwiger proved minimum degree is at most 2.
Comment by Luke Pebody — April 10, 2017 @ 2:26 pm |
Sorry, I don’t understand this comment. What is the “minimum degree”? It sounds like the smallest degree of a vertex but with that definition,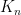 plus an isolated vertex has minimum degree zero, which is certainly at most 2. Can you provide a reference?
plus an isolated vertex has minimum degree zero, which is certainly at most 2. Can you provide a reference?
Comment by tchow8 — April 10, 2017 @ 5:52 pm |
http://cstheory.stackexchange.com/questions/6917/number-of-edges-in-k-4-free-graphs
Comment by domotorp — April 10, 2017 @ 9:33 pm |
Ah, good! Thanks. So it looks like my naive plan is unlikely to succeed. Still, I am wondering if perhaps it is possible to characterize “benign” versus “malignant” occurrences of minors and to figure out how to construct columns inductively in a way that avoids painting oneself into a malignant corner. The paper by Harvey, Kiraly, and Lau should give some important clues about what kinds of malignancies can arise.
minors and to figure out how to construct columns inductively in a way that avoids painting oneself into a malignant corner. The paper by Harvey, Kiraly, and Lau should give some important clues about what kinds of malignancies can arise.
By the way, I think it’s also worth mentioning that Marcel Wild has another paper that may be relevant: Base exchange properties of graphic matroids, Discrete Math. 148 (1996), 253-264. Although graphic matroids were mentioned early on in the Polymath project as a possible special case of interest, it hasn’t been clear to me until now what would make the graphic matroid case easier than the general case. But since -minor-free graphs are strongly base orderable, and since graphic matroids are known to have special basis exchange properties that aren’t true in general, I now feel more hopeful that graphic matroids may be more tractable.
-minor-free graphs are strongly base orderable, and since graphic matroids are known to have special basis exchange properties that aren’t true in general, I now feel more hopeful that graphic matroids may be more tractable.
Comment by tchow8 — April 11, 2017 @ 2:28 pm |
I’m having trouble figuring out how to prove that if you delete an element from a base-orderable matroid
from a base-orderable matroid  then the resulting matroid
then the resulting matroid  is still base-orderable. Of course if the rank
is still base-orderable. Of course if the rank  equals the rank
equals the rank  then this is obvious, but if
then this is obvious, but if 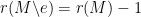 then the obvious line of argument is to extend the given bases
then the obvious line of argument is to extend the given bases 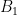 and
and 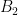 of
of  to bases
to bases  and
and  of
of  , then restrict the bijection
, then restrict the bijection  to
to 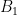 . The thing I’m worried about is that maybe
. The thing I’m worried about is that maybe 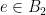 and
and  sends some element of
sends some element of 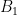 to
to  , in which case
, in which case  does not restrict to a bijection between
does not restrict to a bijection between 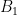 and
and 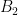 .
.
I’m confident the result is true because I see it stated everywhere. Welsh’s book even gives a proof but it’s essentially the above argument and so it looks to me as though it has a gap. Oxley’s book states it as an exercise and cites the literature, but when I looked up the papers the terminology was sufficiently different that I couldn’t figure out how to extract what I wanted. Can someone else help?
Comment by tchow8 — March 23, 2017 @ 1:58 am |
O.K., I see what I was missing now:
Fact. Let be base-orderable. Let
be base-orderable. Let 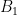 and
and 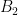 be bases of
be bases of  , and let
, and let  be a bijection whose existence is guaranteed by the base-orderability axiom. Then
be a bijection whose existence is guaranteed by the base-orderability axiom. Then  restricted to
restricted to  must be the identity map.
must be the identity map.
The proof is obvious as soon as you think about it: If and
and  is not the identity map, then
is not the identity map, then  contains “two copies of
contains “two copies of  ” and hence cannot be a basis.
” and hence cannot be a basis.
So now returning to the “obvious line of argument” in my comment above, if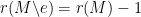 then that must mean that every basis of
then that must mean that every basis of  contains
contains  . In particular,
. In particular,  and
and  must both contain
must both contain  , and by the above Fact,
, and by the above Fact,  is the identity on
is the identity on  . So
. So  does indeed restrict to a bijection between
does indeed restrict to a bijection between 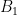 and
and 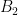 , and we’re done.
, and we’re done.
I am now hopeful about proving Rota’s Basis Conjecture for base-orderable matroids, which would generalize Wild’s result that the conjecture holds for strongly base-orderable matroids.
Comment by tchow8 — March 28, 2017 @ 2:52 pm |
Some remarks on Alon-Tarsi conjecture as a correlation inequality (that Tim asked about). (I inquired a few random matrices friends and this comment reflects also a discussion with Ofer Zeitouni and remarks by Krzysztof Oleszkiewicz and Ron Peled).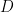 and consider an
and consider an 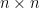 random matrix
random matrix  with entries i.i.d. from
with entries i.i.d. from 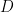 and consider the expectation
and consider the expectation
Start with any symmetric (around zero) real probability distribution
When you evaluate this expectation in terms of monomials in the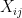 the contribution of monomials that appears with degree one is zero. (Because
the contribution of monomials that appears with degree one is zero. (Because 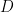 is symmetric around zero). The contribution to the monomial
is symmetric around zero). The contribution to the monomial
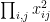 is precisely a signed summation of Latin squares. This comes from the product of
is precisely a signed summation of Latin squares. This comes from the product of  disjoint generalized diaginals in the expansion of
disjoint generalized diaginals in the expansion of  ,
, permutations representing these generalized diagonals.
permutations representing these generalized diagonals.
The sign is the product of signs of all
This expression does not depend on the distribution, it is zero when is odd, and the common belief that for even values of
is odd, and the common belief that for even values of  there are more even than odd Latin squares gives (I think) that
there are more even than odd Latin squares gives (I think) that
Three comments:
1) I am less optimistic now that this probabilistic interpretation is useful. For Gaussian matrices there are nice expressions for the joint eigenvalues distribution but it does not seem to mix well with the product of entries. Of course the key would be to give another expression for this correlation or a wider context but I dont see any.
2) It would be nice to examine the case for complex distributions and some familiar families of random matrices like random Hermitian matrices.
3) This observation is essentially Theorem 1.9(e) of Kumar and Landsberg’s paper CONNECTIONS BETWEEN CONJECTURES OF ALON-TARSI, HADAMARD-HOWE, AND INTEGRALS OVER THE SPECIAL UNITARY GROUP.
Comment by Gil Kalai — March 10, 2017 @ 8:07 am |
There are very relevant papers by Jeannette Janssen. One classic paper The Dinitz problem solved for rectangles contains a proof based on Alon-Tarsi theorem of a rectangle case of Dinitz conjecture. It is very interesting if the polynomial used by Janssen can beused to prove a “rectangular” (this a bit weaker) case of the Rota conjecture. (Note that a similar slightly weaker form of the conclusion of Rota conjecture is conjectured by Ron Aharoni in much greater generality.) The other paper is On even and odd Latin squares. It contains the relation between the various definitions of signs of matrices (mentioned in my previous comment). Another remark is that the conjecture that there are more even Latin squares than odd ones may well be a wishful thinking based on a few very small cases. I wonder if somebody can offer a heuristic explanation why this should be true.
Comment by Gil Kalai — March 14, 2017 @ 8:07 am |
As a starting point for a heuristic argument that there are more even Latin squares than odd ones, we might note that the number of even derangements of minus the number of odd derangements of
minus the number of odd derangements of  is
is  . Admittedly, I’m not quite sure what to do with this observation…
. Admittedly, I’m not quite sure what to do with this observation…
Comment by tchow8 — March 28, 2017 @ 3:11 am |
This means that the number of row-even partial Latin squares minus the number of row-odd partial
Latin squares minus the number of row-odd partial  Latin squares is
Latin squares is
 .
.
Clearly for this difference will be 0, so maybe we should instead consider partial
this difference will be 0, so maybe we should instead consider partial 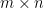 matrices where the first row is
matrices where the first row is 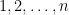 .
.
Then for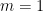 the difference is 1, for
the difference is 1, for  , it is
, it is  ,
,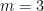 , it is 0, 0, 2, 0, 72, -320, 3600, -32256, …, which is at http://oeis.org/A098276. For
, it is 0, 0, 2, 0, 72, -320, 3600, -32256, …, which is at http://oeis.org/A098276. For 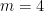 , the sequence starts 0,0,0,24,-576,12960.
, the sequence starts 0,0,0,24,-576,12960.
and for
Comment by Luke Pebody — March 28, 2017 @ 4:59 am |
It may be worth mentioning that Levent Alpoge has used the Kumar–Landsberg result to estimate the size of the Alon–Tarsi constant. Unfortunately, from the point of view of Rota’s Basis Conjecture, he provides only an upper bound rather than a lower bound, but I think it is still an interesting result.
Comment by tchow8 — March 20, 2017 @ 6:29 pm |
[…] the occasion of Polymath 12 devoted to the Rota basis conjecture let me remind you about the Alon-Tarsi conjecture and test […]
Pingback by Test Your Intuition about the Alon-Tarsi Conjecture | Combinatorics and more — March 15, 2017 @ 10:29 am |
Let me provide another possible inductive approach: be a sequence split into some subsequences
be a sequence split into some subsequences  (called color classes).
(called color classes).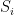 .
.
Let
We say that another subsequence is rainbow, if it contains at most one element from each
Now the lemma: (from https://arxiv.org/abs/1702.08170) be a matroid of rank
be a matroid of rank  and
and  be a sequence of
be a sequence of 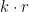 elements from
elements from  ,
, subsequences, each of length at most
subsequences, each of length at most  .
. is a basis of
is a basis of 
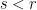 and set of
and set of  color classes, such that the union of these color classes has rank
color classes, such that the union of these color classes has rank  .
.
Let
split into
Then any largest independent rainbow subsequence of
if and only if (*) there does not exist an integer
The idea would be to remove the largest independent rainbow set, leaving elements and use recursion. This of course does not always work, in many cases the remaining elements will not satisfy (*),
elements and use recursion. This of course does not always work, in many cases the remaining elements will not satisfy (*),
but it seems to me that in this case one can try to use some backtracking (going several steps back if necessary) and exchange axiom to force (*).
Comment by Pavel Paták — March 23, 2017 @ 9:13 am |
This is an interesting idea. My guess is that a more promising approach than backtracking is to try to modify/generalize the lemma to make the induction/recursion go through without backtracking. Once you start backtracking, it becomes difficult to keep track of all the different cases that could arise.
More specifically, can you give examples of how (*) can fail after a basis is removed? Then we could think about what conditions are needed to ensure that this scenario can’t happen. That will require modifying the induction hypothesis and maybe force more conditions, but hopefully the modification process will eventually converge.
Comment by tchow8 — March 28, 2017 @ 1:27 am |
Is Rota’s basis conjecture]implied by the same statement restricted to vector spaces over a fixed field (say , or even
, or even 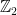 )?
)?
Comment by dominiczypen — March 28, 2017 @ 6:17 am |
This is not known.
Comment by tchow8 — March 28, 2017 @ 2:41 pm |
I wonder if the following version of colorful Tverberg theorem is correct. Consider (affinely independent) subsets of size
(affinely independent) subsets of size  of
of 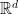 such that the origin belongs to the interior of the convex hull of each set. Is it possible to find
such that the origin belongs to the interior of the convex hull of each set. Is it possible to find  sets of size
sets of size  such that each set is a rainbow set and the interior of the convex hulls of all these sets have a point in common.
such that each set is a rainbow set and the interior of the convex hulls of all these sets have a point in common.
Comment by Gil Kalai — March 31, 2017 @ 10:36 am |
I would have a couple of questions regarding this very interesting conjecture.
1, Why is affinely independent needed?
2, In the conclusion, why are you asking for an arbitrary point in common instead of the origin?
3, Is the condition that the origin is in the convex hulls known to be needed for the conclusion? (I know that a topological version of Tverberg’s theorem has been disproved, but the current statement is about convex hulls.)
Comment by domotorp — April 1, 2017 @ 9:12 am |
Well, there are few versions of this conjecture that can be asked. For the condition you can ask that
a) The points in each set are affinely independent and
b) That the origin is in the interior of their convex hull.
And for the conclusion you can ask that
1) There are d+1 rainbow sets so that there is a point in their intersection and
2) There are d+1 rainbow sets such that the origin is in the interior of their intersection.
(Of course, b is stronger than a and 2 is stronger than 1.)
I asked if b implies 1. We can also make two stronger conjectures that a implies 1 and that b implies 2.
Now there is a conjecture by Reay that says that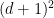 points in general conjecture have a partition into
points in general conjecture have a partition into  sets (necessarily all of size
sets (necessarily all of size  ) such that the interior of their convex hulls intersect. The conjecture a implies 1 is even stronger. Also b implies 2 seems very strong. In particular, b implies 2 give a very strong form of Barany’s colorful Caratheodory theorem which might be too good to be true.
) such that the interior of their convex hulls intersect. The conjecture a implies 1 is even stronger. Also b implies 2 seems very strong. In particular, b implies 2 give a very strong form of Barany’s colorful Caratheodory theorem which might be too good to be true.
Comment by Gil Kalai — April 1, 2017 @ 8:28 pm |
“b implies 2” is indeed too good to be true. Consider the following sets of points in the plane:
{(-2,2),(1,-2),(2,-1)}, {(-1,-2),(0,2),(1,-2)}, {(-2,-1),(-1,-2),(2,2)}.
Any set containing the origin in its interior must contain a point with positive second coordinate,
so at least one of (-2,2),(0,2),(2,2). If there are 3 disjoint rainbow sets, then each must contain exactly one of (-2,2),(0,2),(2,2).
But there is no rainbow set containing only (-2,2) from this set of points.
Comment by Tamás Király — April 6, 2017 @ 9:08 am |
Dear Tamas, Indeed I think that also a implies 1) is not true. Does your example satisfies 2)?
Comment by Gil Kalai — April 6, 2017 @ 4:22 pm |
Nice! This example seems to suggest that b) doesn’t seem to have much advantage compared to a).
Comment by domotorp — April 6, 2017 @ 7:18 pm |
@domotorp Why is that? is b implies 1 still open?
Comment by Gil Kalai — April 18, 2017 @ 8:43 pm |
It is still open of course, since a) implies 1 is also open. But I wonder if for example it is possible to construct from a d-dim input S satisfying a) a (d+1)-dim input S’ satisfying b) so that if S’ doesn’t satisfy 1, nor does S.
Comment by domotorp — April 19, 2017 @ 4:29 am |
I think I had an example against a) implies 1) but I have to find it.
Comment by Gil Kalai — April 19, 2017 @ 6:48 am |
Wouldn’t that give an example showing that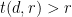 for
for  in the (non-topological) colorful Tverberg problem?
in the (non-topological) colorful Tverberg problem?
Comment by domotorp — April 19, 2017 @ 7:59 am |
Ah I meant another 1) (from the first comment) that there is a point in common to the interior of the simplices. Sorry for the confusion.
Comment by Gil Kalai — April 19, 2017 @ 3:20 pm |
I want to comment on the prospects for generalizing the Geelen–Humphries induction argument to a proof of the full conjecture.
First, as they point out in their paper, the following statement is FALSE:
False claim. Let be disjoint sets of size
be disjoint sets of size 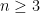 , and let
, and let 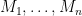 be arbitrary rank
be arbitrary rank  matroids on
matroids on  such that
such that 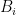 is a basis of
is a basis of 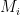 for each
for each  . Then there exist
. Then there exist  disjoint transversals
disjoint transversals  of
of  such that
such that 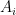 is a basis of
is a basis of 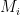 for each
for each  .
.
This is false for a rather trivial reason. The only control you have over the structure of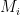 is that
is that 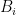 is a basis, and the elements of the other
is a basis, and the elements of the other  could even be loops in
could even be loops in 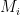 (in the context of vector spaces, a “loop” is a copy of the zero vector). So if we want to prove Rota’s Basis Conjecture for all matroids this way, we need to impose some additional conditions on the
(in the context of vector spaces, a “loop” is a copy of the zero vector). So if we want to prove Rota’s Basis Conjecture for all matroids this way, we need to impose some additional conditions on the 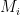 —strong enough to block this kind of counterexample, but weak enough that we can specialize to the case
—strong enough to block this kind of counterexample, but weak enough that we can specialize to the case 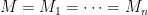 and infer Rota’s Basis Conjecture for an arbitrary rank
and infer Rota’s Basis Conjecture for an arbitrary rank  matroid.
matroid.
At first I thought that insisting that all the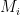 be minors of the same matroid should buy us something, but Jim Geelen pointed out to me by email that given any two matroid structures
be minors of the same matroid should buy us something, but Jim Geelen pointed out to me by email that given any two matroid structures 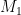 and
and 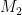 on a common ground set
on a common ground set 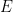 , there exists some matroid
, there exists some matroid  that has both
that has both 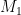 and
and 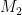 as minors. So that’s not enough.
as minors. So that’s not enough.
Here is another remark. The Geelen–Humphries induction is based on the following construction: We start by figuring out how to arrange the first row and the first column of the desired grid, and (this is the Key Lemma) we do this in such a way that if we swap the first element in row with the first element in column
with the first element in column  , then row
, then row  remains a basis. Then we apply induction to arrange the remaining
remains a basis. Then we apply induction to arrange the remaining 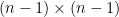 elements, without disturbing the first row and column. It is therefore natural to ask if this general framework has any hope of proving the full conjecture. That is, suppose we are given
elements, without disturbing the first row and column. It is therefore natural to ask if this general framework has any hope of proving the full conjecture. That is, suppose we are given  bases of the same matroid, as in the original Rota Basis Conjecture. Suppose the first column and the first row are arranged so that the first column is a basis, and that for every
bases of the same matroid, as in the original Rota Basis Conjecture. Suppose the first column and the first row are arranged so that the first column is a basis, and that for every  , swapping the first element in row
, swapping the first element in row  with the first element in column
with the first element in column  leaves row
leaves row  a basis. Then does there necessarily exist a rearrangement of the remaining
a basis. Then does there necessarily exist a rearrangement of the remaining 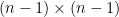 elements (without disturbing the first row and column) that satisfies the conclusion of Rota’s Basis Conjecture?
elements (without disturbing the first row and column) that satisfies the conclusion of Rota’s Basis Conjecture?
Unfortunately, the answer is no, and a simple counterexample is again provided by our old friend . Let’s take the rows to be the bases
. Let’s take the rows to be the bases  ,
,  , and
, and 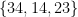 , in that order. The first column and the first row are equal, so the swapping condition is trivially satisfied. On the other hand, it is easily checked that there is no way to make all three columns be bases without disturbing the first column.
, in that order. The first column and the first row are equal, so the swapping condition is trivially satisfied. On the other hand, it is easily checked that there is no way to make all three columns be bases without disturbing the first column.
I had been hoping that because the Geelen–Humphries induction goes from an square to an
square to an 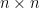 square without passing explicitly through non-square rectangles, we might be able to sidestep the
square without passing explicitly through non-square rectangles, we might be able to sidestep the  obstruction. It looks like that is not possible. It’s still conceivable to me that if we choose the first column more delicately, we can still make this kind of induction argument work, but once again it looks like we have to come to grips with “local obstructions” like
obstruction. It looks like that is not possible. It’s still conceivable to me that if we choose the first column more delicately, we can still make this kind of induction argument work, but once again it looks like we have to come to grips with “local obstructions” like  .
.
Comment by tchow8 — March 31, 2017 @ 3:54 pm |
I have a more interesting example to show that all sets of size k being independent in all the matroids is not sufficient to prove the many-matroids version of RBC for rank 2k (even when all rows are independent in all the spaces).
In my example, the first 2k-1 matroids are all the same, and are the union of the k-uniform matroid on the left half of the grid and the k-uniform matroid on the right half of the grid. (By k-uniform I mean that all k element sets are independent, but no k+1 element sets are)
It is clear that this is of rank 2k and that a set of size 2k is independent if exactly k elements are in the left half. In particular, all the rows are independent.
Now if we have k-1 independent disjoint transversals from this matroid, the remaining elements will also be an independent transversal from this matroid.
For the final matroid, we take the same matroid except we switch the left elements and right elements on one row. Any set of size 2k that had exactly one element on that row could not be independent in both this matroid and the original matroid, so no complete rainbow exists.
Comment by Luke Pebody — March 31, 2017 @ 6:27 pm |
I’m still hoping that someone will do a computational search for counterexamples consisting of five sets of independent sets of size 2. If nobody else does it then I guess I will eventually do it, although I’m not that great a programmer. Let me mention that Mayhew and Royle have found all matroids with nine elements, so that should simplify the calculation; using their database, we can quickly populate 9 of the 10 slots in the grid, and then run through all the possibilities for adding a 10th element. The ideas described in Mayhew and Royle’s paper should be helpful, although they focus a lot of attention on eliminating isomorphic copies, and that’s not so important for our calculation (presumably there won’t be that many counterexamples, especially if we don’t bother with configurations that contain among the first 9 elements, and so isomorphism testing can be carried out as a post-processing step).
among the first 9 elements, and so isomorphism testing can be carried out as a post-processing step).
Comment by tchow8 — April 1, 2017 @ 12:21 am |
That seems like it would be really useful, but the link to the db at http://people.csse.uwa.edu.au/gordon/small-matroids.html no longer works.
Comment by Luke Pebody — April 1, 2017 @ 7:11 am |
I wrote to Gordon Royle and his reply appears below.
Yes, my site was lost when I moved department…
Here is a link
https://cloudstor.aarnet.edu.au/plus/index.php/s/GBZYfixUsmaRzbO
Unzip the file and it lists the bases of each matroid, one per line in a format similar to the following:
63 5 3 10 ‘012’ ‘013’ ‘023’ ‘123’ ‘014’ ‘024’ ‘124’ ‘034’ ‘134’ ‘234′
This means
“Matroid number 63 has size 5, rank 3 and has 10 bases, which are {0,1,2}, {0,2,3}, {1,2,3}, …, {2,3,4}”
Enjoy…
Gordon
Comment by tchow8 — April 3, 2017 @ 3:01 pm |
The index numbers of the matroids on at most 9 elements which are of rank at most 5, are the union of two independent sets and can have some disjoint pairs such that whenever you express the matroid as a union of two independent sets, some pair is contained in one of the two parts are:
ground set of size 6: [130]
ground set of size 7: [381]
ground set of size 8: [1009, 1042, 1089, 1129, 1135, 1144, 1157, 1196, 1207, 1213, 1216, 1217, 1218, 1232, 1245, 1915]
ground set of size 9: [194069, 194127, 194232, 194452, 194459, 194475, 194488, 195069, 195070, 195086, 195095, 195099, 195100, 195101, 195103, 195104, 195105, 195106, 195107, 195108, 195135, 195157]
It’s possible there are more of size 9. Will confirm later.
Comment by Luke Pebody — April 4, 2017 @ 4:28 am |
Confirmed. This list is complete.
Comment by Luke Pebody — April 4, 2017 @ 4:50 am |
Michael Nielsen and Terry Tao created a page on the Polymath Wiki about Rota’s Basis Conjecture, and I have been fleshing it out. It is still unfinished, particularly the section on partial results, but the References section should be pretty complete. If anyone sees a reference that I have missed, please comment here and I will add it.
Let me highlight two references that I personally feel deserve extra attention. The first is the paper by Marcel Wild. I have already mentioned it but I have never fully digested it, and glancing at it now, I think that it deserves closer scrutiny. The second is an unpublished manuscript of Michael Cheung that claims to computationally check Rota’s Basis Conjecture for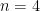 for all matroids. I’m a little surprised that this computation is feasible, given how many 16-element matroids there are, so it would be good for someone to verify it.
for all matroids. I’m a little surprised that this computation is feasible, given how many 16-element matroids there are, so it would be good for someone to verify it.
Comment by tchow8 — April 6, 2017 @ 3:21 am |
I’ve started reading Marcel Wild’s paper more carefully and one thing I noticed, which I had either not noticed before or totally forgotten about, was that he has an interesting partial result about graphic matroids. If I’m reading it correctly, Theorem 3 says that if has maximum degree
has maximum degree  then it is possible to construct
then it is possible to construct 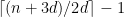 columns of the desired grid. (Wild says "rows" instead of "columns" because his notation is the transpose of ours.)
columns of the desired grid. (Wild says "rows" instead of "columns" because his notation is the transpose of ours.)
This seems to be a pretty strong result for small . Now if
. Now if  is small, then the bases necessarily overlap a lot, so it's certainly a special case, but still interesting I think. I will try to understand the proof technique better and describe it in a future comment.
is small, then the bases necessarily overlap a lot, so it's certainly a special case, but still interesting I think. I will try to understand the proof technique better and describe it in a future comment.
Comment by tchow8 — April 17, 2017 @ 3:29 pm |
I believe I understand Wild’s proof now. He uses Rado’s theorem to construct the columns one at a time, and uses the low degree of the graph to show that the process can be continued for the stated number of columns.
I don’t think we’ve mentioned Rado’s theorem explicitly in Polymath 12 yet. It’s a generalization of Hall’s marriage theorem. If you have sets of elements from a matroid such that for all
of elements from a matroid such that for all 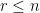 , the rank of the union of any
, the rank of the union of any  of the sets is at least
of the sets is at least  , then there is an independent set
, then there is an independent set 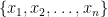 such that
such that  for all
for all  .
.
Suppose now that we have a simple graph (i.e., no loops or multiple edges) with no isolated vertices, and let
(i.e., no loops or multiple edges) with no isolated vertices, and let  be the rank of the associated matroid. Rota’s Basis Conjecture hypothesizes that we have
be the rank of the associated matroid. Rota’s Basis Conjecture hypothesizes that we have  bases
bases 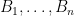 . Constructing the first column of the desired grid is easy, but let us do it by applying Rado’s theorem. We have to check that for all
. Constructing the first column of the desired grid is easy, but let us do it by applying Rado’s theorem. We have to check that for all  , the rank of the union of any
, the rank of the union of any  of the
of the 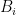 is at least
is at least  . But even one of the
. But even one of the 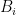 has rank
has rank  by definition, so everything is O.K.
by definition, so everything is O.K.
Now let denote the
denote the 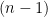 -element set obtained from
-element set obtained from 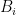 by deleting the element that was chosen to be in the first column. To construct the second column, Wild’s key observation is that if the maximum degree
by deleting the element that was chosen to be in the first column. To construct the second column, Wild’s key observation is that if the maximum degree  of
of  is sufficiently small, then the sets
is sufficiently small, then the sets  will necessarily satisfy Rado’s theorem. If
will necessarily satisfy Rado’s theorem. If 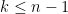 , then we are done because even a single
, then we are done because even a single  will have rank at least
will have rank at least  , so we just need to check that the union of all the
, so we just need to check that the union of all the  has rank
has rank  . Here is where the structure of the graph comes in.
. Here is where the structure of the graph comes in.
Wild defines the “capacity” of a vertex to be the number of edges among the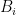 that are incident to it, counting multiplicities. Now, if
that are incident to it, counting multiplicities. Now, if  is any vertex of
is any vertex of  , then every one of the original bases
, then every one of the original bases 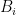 contains an edge that is incident to
contains an edge that is incident to  , because a basis by definition comprises a spanning tree for each connected component of
, because a basis by definition comprises a spanning tree for each connected component of  ; thus the capacity of
; thus the capacity of  is at least
is at least  . When we delete the first column, the capacity of
. When we delete the first column, the capacity of  drops by at most
drops by at most  , since the first column is a basis and cannot contain multiple copies of an edge that is incident to
, since the first column is a basis and cannot contain multiple copies of an edge that is incident to  . Thus if
. Thus if  , then the union of the
, then the union of the  must contain some edge incident to
must contain some edge incident to  . Since
. Since  was arbitrary, this means that the union of the
was arbitrary, this means that the union of the  contains a spanning subgraph of
contains a spanning subgraph of  , and hence its rank is
, and hence its rank is  , as desired.
, as desired.
For the third column, we let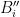 be
be  minus the element in the second column. We need to check the hypothesis of Rado’s theorem for the
minus the element in the second column. We need to check the hypothesis of Rado’s theorem for the 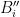 with
with  and
and  . For
. For  , the same argument as before shows that the rank of the union of all the
, the same argument as before shows that the rank of the union of all the 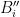 is at least
is at least  as long as
as long as  . For
. For  , we can think of the union of
, we can think of the union of  of the
of the 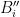 as being obtained by removing, from the original
as being obtained by removing, from the original 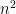 elements, three sets: the first column, the second column, and one of the rows (i.e., one of the
elements, three sets: the first column, the second column, and one of the rows (i.e., one of the 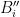 ). Each of these three sets is independent and hence can reduce the capacity of a vertex by at most
). Each of these three sets is independent and hence can reduce the capacity of a vertex by at most  , so if
, so if 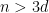 then the union of
then the union of  of the
of the 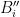 must contain a spanning subgraph of
must contain a spanning subgraph of  , and therefore has rank
, and therefore has rank  , which is more than enough (we only need rank
, which is more than enough (we only need rank  to invoke Rado’s theorem).
to invoke Rado’s theorem).
In general, to get the th column for
th column for  , we need to verify the hypothesis of Rado’s theorem for
, we need to verify the hypothesis of Rado’s theorem for  . Deleting
. Deleting 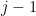 columns and
columns and  rows reduces the capacity of a vertex by at most
rows reduces the capacity of a vertex by at most  , so as long as
, so as long as  (i.e., as long as
(i.e., as long as  ) then Rado's theorem does the trick. This proves Wild's result.
) then Rado's theorem does the trick. This proves Wild's result.
Comment by tchow8 — April 20, 2017 @ 3:11 am |
On the topic of graphs, I learned recently that there are some graph-theoretic conjectures with the same flavor as Rota’s Basis Conjecture. For example, a recent arXiv preprint by Horn and Nelsen proves a new partial result towards an old conjecture of Brualdi and Hollingsworth, which says that if the complete graph (for
(for  ) is edge-colored in such a way that every color class is a perfect matching, then there is a decomposition of the edges into
) is edge-colored in such a way that every color class is a perfect matching, then there is a decomposition of the edges into  edge-disjoint rainbow spanning trees (“rainbow” means that no two edges in the spanning tree have the same color). While I don’t see any direct connection with Rota’s Basis Conjecture, perhaps some of the proof techniques carry over from one setting to the other.
edge-disjoint rainbow spanning trees (“rainbow” means that no two edges in the spanning tree have the same color). While I don’t see any direct connection with Rota’s Basis Conjecture, perhaps some of the proof techniques carry over from one setting to the other.
Comment by tchow8 — April 17, 2017 @ 8:19 pm |
Jeff Kahn mentioned to me the beautiful “Wide Partition Conjecture” from the paper: T. Chow, C.K. Fan, M.X. Goemans and J. Vondrak, Wide Partitions, Latin Tableaux, and Rota’s Basis Conjecture, Advances in Applied Mathematics, 31, 334–358, 2003. pdf . (I think this conjecture might be interesting also in the Tverberg context we mensioned above.) Perhaps, Tim, you can explain and motivate this conjecture and its relation to Rota’s conjecture?
Comment by Gil Kalai — April 17, 2017 @ 8:39 pm |
Brian Taylor and I noticed that in the context of bracket algebras, which were Rota’s original motivation, there was nothing special about square shapes; one could consider any Young diagram. We thought that generalizing Rota’s Basis Conjecture to Young diagrams might open up the possibility of proofs by induction that add a single box at a time. We did find a successful generalization to Young diagrams that we called the “wide partition conjecture”; unfortunately, it seems that this generalization makes life harder, not easier, so I don’t think that this is a promising avenue to proving Rota’s Basis Conjecture. However, there is a certain special case of the wide partition conjecture that is interesting and tantalizing in its own right, which I will now describe.
Given a Young diagram with row lengths
with row lengths  , we can ask, is there a way to put a number in each box in such a way that (A) in row
, we can ask, is there a way to put a number in each box in such a way that (A) in row  , each number from
, each number from  to
to  appears exactly once, and (B) in every column, the numbers that appear are all distinct? In general the answer is certainly no; for example, in a Young diagram that consists entirely of a single column, condition (A) forces you to put a 1 in each box, and this violates condition (B) as soon as there is more than one box in the column. If you study the problem for a bit, you will soon see that a necessary condition for a positive answer to the question is that
appears exactly once, and (B) in every column, the numbers that appear are all distinct? In general the answer is certainly no; for example, in a Young diagram that consists entirely of a single column, condition (A) forces you to put a 1 in each box, and this violates condition (B) as soon as there is more than one box in the column. If you study the problem for a bit, you will soon see that a necessary condition for a positive answer to the question is that  , where
, where 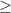 denotes dominance (a.k.a. majorization) order, and
denotes dominance (a.k.a. majorization) order, and  denotes the conjugate (a.k.a. transpose) of
denotes the conjugate (a.k.a. transpose) of  . Moreover, if
. Moreover, if 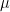 is any Young diagram whose multiset of rows is a submultiset of the multiset of rows of
is any Young diagram whose multiset of rows is a submultiset of the multiset of rows of  , then we must have
, then we must have  as well. The wide partition conjecture states that this necessary condition is also sufficient.
as well. The wide partition conjecture states that this necessary condition is also sufficient.
By the way, this special case of the wide partition conjecture would follow from another conjecture that I described on MathOverflow a couple of years ago.
Comment by tchow8 — April 17, 2017 @ 9:30 pm |
Tim, three quick questions: For this conjecture (in the special case you mentioned) what do we get for the square case? Is there an analogue of Galvin’s theorem, and is there an analog of the Alon-Tarsi connection? (The paper said that this is likely but not yet verified.)
Comment by Gil Kalai — April 18, 2017 @ 8:50 pm |
For square shapes, the conjecture reduces to the trivial statement that “Latin squares exist.” As for Galvin, the theorem he proved was about the list chromatic index of an arbitrary bipartite multigraph, so it already says something about Young diagrams, but I’m not sure if that’s what you’re asking. Maybe you’re asking for an analogue of the Dinitz conjecture for Young diagrams? The closest thing I know is Theorem 1 in our paper, but that’s probably not quite what you want.
Finally, as you noted, in the paper we already said that it ought to be easy to formulate an Alon-Tarsi conjecture for Young diagrams, but I don’t think anybody has bothered to work out the details. Maybe now is a good time to work this out. Towards this end, I would consider shapes that are not only wide (i.e., satisfy the necessary conditions I mentioned above) but are also self-conjugate, because then you can ask for every column, as well as every row, to be a permutation, so that it is clear what “even” and “odd” mean. The analogue of Alon-Tarsi would state that for any wide self-conjugate shape, the number of even tableaux is not equal to the number of odd tableaux. Then the only thing left to check is that this analogue of Alon-Tarsi would imply the analogue of Rota’s Basis Conjecture for self-conjugate wide shapes. What requires some thought is how to deal with the fact that the rows and columns do not all have the same length. Presumably, we should switch from talking about “bases” to talking about “independent sets”; that’s easy enough, but then we’re going to have to deal with non-square matrices, for which linear independence is more complicated to express algebraically (it’s not just the nonvanishing of a single determinant).
Comment by tchow8 — April 18, 2017 @ 10:03 pm |
Continuing the graph-theory angle, here is a hopefully tractable problem that I think would help us make some headway. Consider the two-column version of Rota’s Basis Conjecture. That is, suppose we have disjoint independent sets
disjoint independent sets  , each of size 2, and suppose that their union
, each of size 2, and suppose that their union 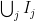 can be written as the disjoint union of two bases. Then is there an
can be written as the disjoint union of two bases. Then is there an 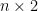 grid whose
grid whose  th row is
th row is  and whose two columns are bases? We know that the answer in general is no because
and whose two columns are bases? We know that the answer in general is no because  is a counterexample already for
is a counterexample already for 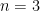 , and we also know that the answer is yes for strongly base-orderable matroids (which, in the case of graphs, coincide with series-parallel graphs). My question is, if we restrict our attention to graphic matroids, can we characterize the counterexamples? We know that there has to be a
, and we also know that the answer is yes for strongly base-orderable matroids (which, in the case of graphs, coincide with series-parallel graphs). My question is, if we restrict our attention to graphic matroids, can we characterize the counterexamples? We know that there has to be a  minor somewhere. But do there have to exist three sets
minor somewhere. But do there have to exist three sets  that are an explicit copy of
that are an explicit copy of  ? My guess is no, but I would like to see some explicit examples.
? My guess is no, but I would like to see some explicit examples.
While the case of two columns may seem very special, as I showed in one of my papers, in some situations one can reduce Rota’s Basis Conjecture to the case of two columns.
Comment by tchow8 — April 20, 2017 @ 3:31 pm |
Just as a trivial way of making a more complicated example:
a1x vs a2x a2x Vs a1x a1b Vs cd a1c Vs bd a2d Vs BC
Comment by Luke Pebody — April 20, 2017 @ 5:12 pm |
Could you please decipher this notation?
Comment by domotorp — April 20, 2017 @ 7:36 pm |
Yeah, that did turn out more cryptic than I had hoped.
The blue and green edges at the top mean that the top three edges must be connected in blue and green, so we can contract those edges and then the remaining coloured edges make a
Comment by Luke Pebody — April 21, 2017 @ 7:16 am |
This is a nice observation. Thinking about where to go from here, I was led to the following thought. Given a graph, let us define the operation of “pulling out an edge” to mean deleting the edge, and then adding two new vertices to the graph with a new edge between them. Question: Given an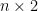 graphic counterexample to the two-column version of Rota’s Basis Conjecture, can we always fix it by pulling out at most
graphic counterexample to the two-column version of Rota’s Basis Conjecture, can we always fix it by pulling out at most 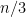 edges?
edges?
I expect that the answer is probably no, but the counterexamples should be more interesting, because I don’t think you can get them just by stringing together disjoint copies of and “uncontracting” edges as in Luke Pebody’s example.
and “uncontracting” edges as in Luke Pebody’s example.
Should the answer unexpectedly be yes, then that gives hope that we can control the copies of . Pulling out edges can be thought of as a proxy for making sure that those edges get used in other columns, in some kind of induction argument.
. Pulling out edges can be thought of as a proxy for making sure that those edges get used in other columns, in some kind of induction argument.
Comment by tchow8 — April 24, 2017 @ 5:12 pm |
Could you be more precise? By putting out, you really want to add an independent edge to the graph? What is “fixing it?” Does it mean converting it to something that’s not a counterexample?
Comment by domotorp — April 24, 2017 @ 7:33 pm |
By “fixing it” I do mean converting it to something that’s not a counterexample. And yes, when I pull out an edge , I first delete
, I first delete  , and then I add a new independent edge
, and then I add a new independent edge  to the graph. If
to the graph. If  originally appeared in the two-element independent set
originally appeared in the two-element independent set  , then
, then  replaces
replaces  in
in  . Another way to put it is that I alter the matroid by making all sets consisting of an independent set plus the given edge independent, and keeping all the other independent sets. Basically I want to delete the edge from the graph (because I’m imagining that this is just an inductive step in the ordinary Rota conjecture, and the edge is appearing in some other column) but technically I have to leave it in there because the two-column version of the conjecture involves exactly
. Another way to put it is that I alter the matroid by making all sets consisting of an independent set plus the given edge independent, and keeping all the other independent sets. Basically I want to delete the edge from the graph (because I’m imagining that this is just an inductive step in the ordinary Rota conjecture, and the edge is appearing in some other column) but technically I have to leave it in there because the two-column version of the conjecture involves exactly  sets of size exactly 2.
sets of size exactly 2.
Comment by tchow8 — April 25, 2017 @ 12:05 am |
But what happens to the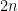 elements’ partitioning to two bases? You forget about that condition? I might be really misunderstanding something, but consider taking the original
elements’ partitioning to two bases? You forget about that condition? I might be really misunderstanding something, but consider taking the original  matrix ordered such that the first column forms a basis. The second column can be covered by two independent sets (the respective parts of the two original bases). One of these independent sets will have at most
matrix ordered such that the first column forms a basis. The second column can be covered by two independent sets (the respective parts of the two original bases). One of these independent sets will have at most  elements. Why can’t we pull these out?
elements. Why can’t we pull these out?
Comment by domotorp — April 25, 2017 @ 8:48 am |
I’m afraid I don’t understand your sentence, “One of these independent sets will have at most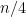 elements.” Of course, by the pigeonhole principle, one of these independent sets will have at most
elements.” Of course, by the pigeonhole principle, one of these independent sets will have at most 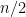 elements, but how are you getting
elements, but how are you getting 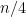 ? In fact if we look at our favorite example of
? In fact if we look at our favorite example of  with
with 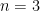 , then we see that
, then we see that 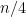 cannot be achieved.
cannot be achieved.
Comment by tchow8 — April 25, 2017 @ 5:01 pm |
Oops, right, somewhere halfway through my argument I forgot that was not the total number of elements.
was not the total number of elements.
Comment by domotorp — April 25, 2017 @ 6:11 pm
Given sets of size
sets of size  in an
in an  -dimensional vector space
-dimensional vector space 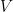 it would be interesting to find various sufficient and necessary conditions for finding
it would be interesting to find various sufficient and necessary conditions for finding  rainbow disjoint basis
rainbow disjoint basis  . So here is a tentative question: If this is not possible can you always find disjoint
. So here is a tentative question: If this is not possible can you always find disjoint 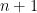 sets,
sets, 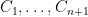 such that each set contains at most one member from each
such that each set contains at most one member from each  and the intersection of all linear spans of the
and the intersection of all linear spans of the 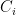 s is non trivial. (Remark: we identify members of the
s is non trivial. (Remark: we identify members of the 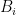 ‘s by their index, and in case of repeated vectors for the purpose of “at most one” and “disjoint” we refer to this indexing.)
‘s by their index, and in case of repeated vectors for the purpose of “at most one” and “disjoint” we refer to this indexing.)
Comment by Gil Kalai — April 26, 2017 @ 12:05 pm |
This sounds like an interesting idea, but can you provide some motivation for the condition that you state? I’m having a hard time understanding why one would expect this to be true.
Comment by tchow8 — April 28, 2017 @ 2:15 pm |
I’ve been continuing to read Wild’s 1994 paper and I think that the most interesting thing in it that I’ve not mentioned already is Lemma 6, which states the following.
Let be a matroid on an
be a matroid on an 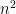 -element set
-element set 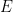 that is a disjoint union of
that is a disjoint union of  independent sets
independent sets 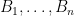 of size
of size  . Assume that there exists another matroid
. Assume that there exists another matroid  on the same ground set
on the same ground set 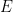 with the following properties:
with the following properties:
(1) is strongly base orderable.
is strongly base orderable.
(2) for all
for all 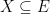 , where
, where  is the rank function of
is the rank function of  .
.
(3) All circuits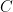 of
of  satisfying
satisfying  remain dependent in
remain dependent in  .
.
Then there is an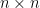 grid whose
grid whose  th row comprises
th row comprises 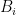 and whose columns are independent in
and whose columns are independent in  .
.
That all strongly base-orderable matroids satisfy Rota’s Basis Conjecture follows at once if we take since condition (2) is automatic by pigeonhole. However, there is a lot more that we might extract out of Lemma 6. Wild asks whether a suitable
since condition (2) is automatic by pigeonhole. However, there is a lot more that we might extract out of Lemma 6. Wild asks whether a suitable  always exists. As Wild recognizes, this is probably too optimistic, but he doesn’t have a counterexample. Maybe a suitable
always exists. As Wild recognizes, this is probably too optimistic, but he doesn’t have a counterexample. Maybe a suitable  always exists for graphic matroids?
always exists for graphic matroids?
Comment by tchow8 — April 28, 2017 @ 2:28 pm |
I have started a new blog post: https://polymathprojects.org/2017/05/05/rotas-basis-conjecture-polymath-12-post-3/ Most new comments should probably be posted under there rather than here.
Comment by tchow8 — May 5, 2017 @ 3:55 am |
Such an insightful read! Your blog consistently delivers valuable content that keeps me engaged and enlightened. Thank you for sharing your knowledge and expertise with us. <a href=”https://adyanthwealth.in/financial-planning/”> Personal Financial Planning </a>
Comment by Anonymous — May 10, 2024 @ 2:47 pm |